4.4.3不同函数的增长差异 课件(共18张PPT)
文档属性
| 名称 | 4.4.3不同函数的增长差异 课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 07:55:16 | ||
图片预览



文档简介
(共18张PPT)
4.4.3不同函数增长的差异
人教A(2019)版
必修一
新知导入
复习巩固
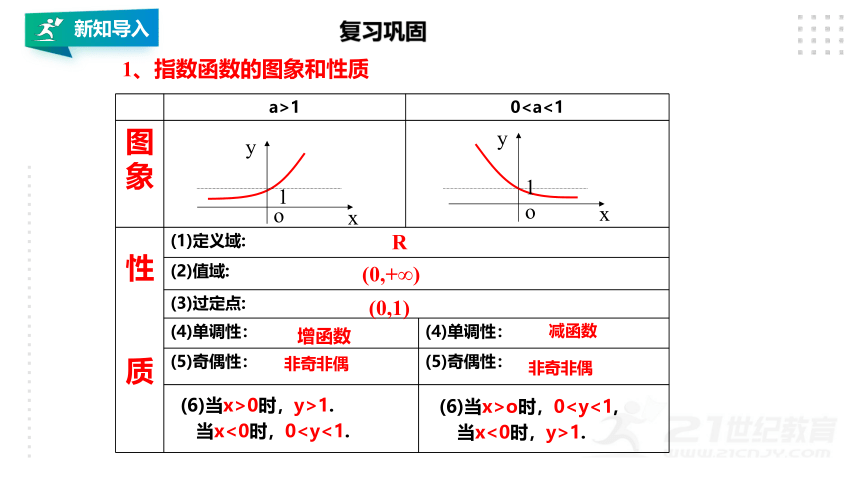
1、指数函数的图象和性质
a>1 0(5)奇偶性: (5)奇偶性:
R
(0,+∞)
(0,1)
增函数
减函数
非奇非偶
非奇非偶
(6)当x>0时,y>1.
当x<0时,0(6)当x>o时,0 当x<0时,y>1.
x
y
o
1
x
y
o
1
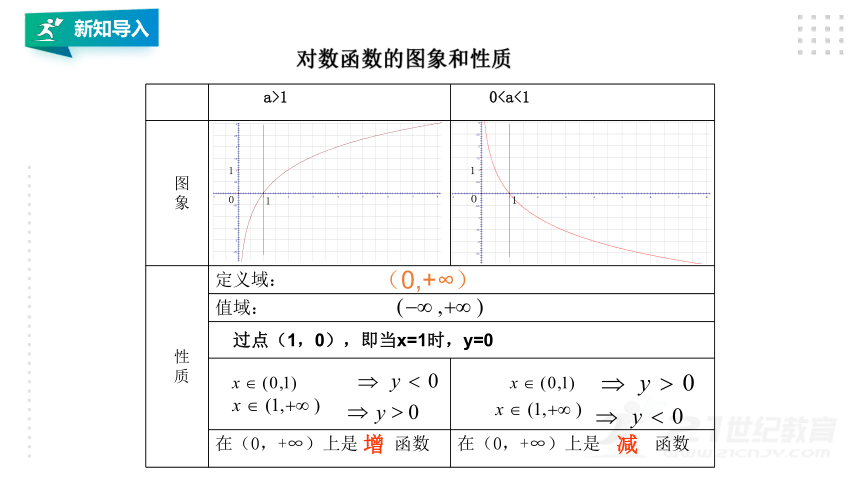
对数函数的图象和性质
a>1 0图 象
性 质 定义域: 值域:
在(0,+∞)上是 函数 在(0,+∞)上是 函数
(0,+∞)
过点(1,0),即当x=1时,y=0
增
减
0
>
y
新知导入
一次函数与指数函数的增长方式存在很大差异.事实上, 这种差异正是不同类型现实问题具有不同增长规律的反映.因此,如果把握了不同函数增长方式的差异,那么就可以根据现实问题的增长情况,选择合适的函数模型刻画其变化规律.下面就来研究一次函数、指数函数和对数函数增长方式的差异.
我们以y=2x和y=2x为例来探讨一下一次函数与指数函数增长的差异
新知讲解
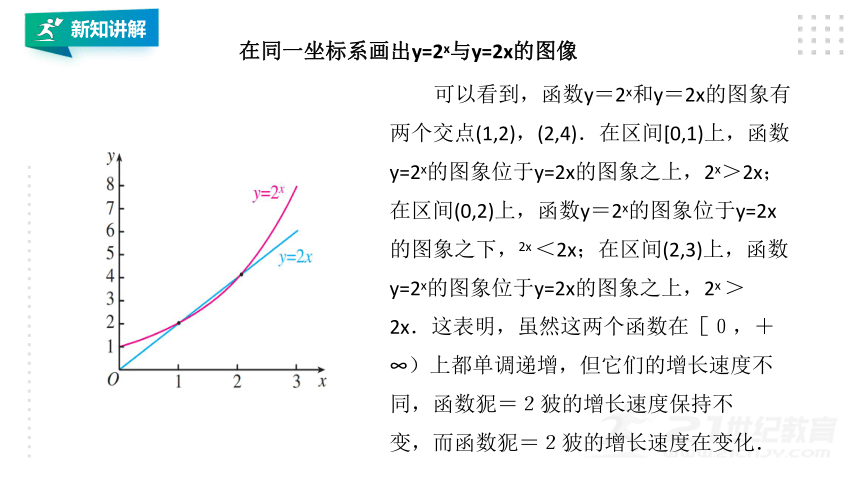
在同一坐标系画出y=2x与y=2x的图像
可以看到,函数y=2x和y=2x的图象有两个交点(1,2),(2,4).在区间[0,1)上,函数y=2x的图象位于y=2x的图象之上,2x>2x;在区间(0,2)上,函数y=2x的图象位于y=2x的图象之下,2x <2x;在区间(2,3)上,函数y=2x的图象位于y=2x的图象之上,2x >2x.这表明,虽然这两个函数在[0,+∞)上都单调递增,但它们的增长速度不同,函数狔=2狓的增长速度保持不
变,而函数狔=2狓的增长速度在变化.
新知讲解
当自变量狓越来越大时,y=2x的图象就像与x轴垂直一样,2x的值快速增长;而函数y=2x的增长速度依然保持不变,与函数y=2x的增长速度相比几乎微不足道.
一般地,指数函数y=ax(a>1)与一次函数y=kx(k>0)的增长差异都与上述情况类似.即使k的值远远大于a的值,y=ax(a>1)的增长速度最终都会大大超过y=kx(k>0)的增长速度.
新知讲解
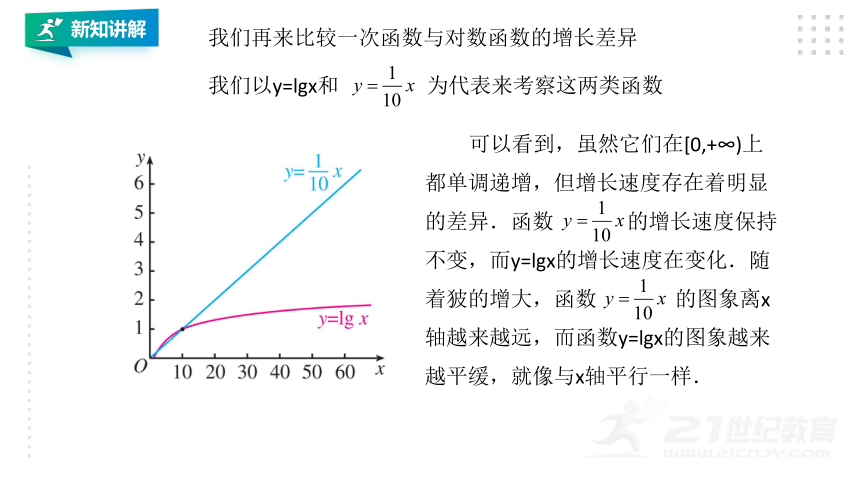
可以看到,虽然它们在[0,+∞)上都单调递增,但增长速度存在着明显的差异.函数 的增长速度保持不变,而y=lgx的增长速度在变化.随着狓的增大,函数 的图象离x轴越来越远,而函数y=lgx的图象越来越平缓,就像与x轴平行一样.
我们再来比较一次函数与对数函数的增长差异
我们以y=lgx和 为代表来考察这两类函数
新知讲解
一般地,虽然对数函数y=logax(a>1)与一次函数y=kx(k>0)在区间(0,+∞)上都单调递增,但它们的增长速度不同.随着x的增大,一次函数y=kx(k>0)保持固定的增长速度,而对数函数y=logax(a>1)的增长速度越来越慢.不论a的值比k的值大多少,在一定范围内,logax可能会大于kx,但由于logax的增长慢于kx的增长,因此总会存在一个x0,当x>x0时,恒有logax<kx.
新知讲解
指数函数 对数函数 一元一次函数
解析式 y=ax(a>1) y=logax(a>1) y=kx(k>0)
单调性 在(0,+∞)上单调递增 图象 逐渐与y轴平行 逐渐与x轴平行 直线逐渐上升
增长速度 越来越快 越来越慢 增长速度不变
存在一个x0,当x>x0时,ax>kx>logax 三种函数的性质及增长速度比较
新知讲解
合作探究
例1、 某公司为了实现1 000万元利润的目标,准备制定一个激励销售部门的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金总数不超过利润的25%.现有三个奖励方案模型:y=0.25x,y=log7x+1,y=1.002x,其中哪个模型能符合该公司的要求
分析:某个奖励模型符合公司要求,就是依据这个模型进行奖励时,奖金总数不超过5万元,同时奖金总数不超过利润的25%,由于公司总的利润目标为1 000万元,所以部门销售利润一般不会超过公司总的利润.
于是,只需在区间[10,1 000],分别检验三个模型是否符合公司要求.
合作探究
解:借助计算机作出函数y=5,y=0.25x,
y=log7x+1,y=1.002x在第一象限内
的大致图象(如图所示):
观察图象发现,在区间[10,1 000]上,模型y=0.25x,y=1.002x的图象都
有一部分在直线y=5的上方,只有模型y=log7x+1的图象始终在y=5的下方,
这说明只有按模型y=log2x+1进行奖励时才符合公司的要求,下面通过计算
确认上述判断.
对于模型y=0.25x,它在区间[10,1 000]上递增,当x∈(20,1 000)时,
y>5,因此该模型不符合要求;
合作探究
对于模型y=1.002x,由函数图象,并利用计算器,可知在区间(805,806)
内有一个点x0满足1.002x=5,由于它在区间[10,1 000]上递增,因此当x>x0时,
y>5,因此该模型y=1.002x也不符合要求;
对于模型y=log7x+1,它在区间[10,1000]上递增,而且当x=1000时,
y=log71 000+1≈4.55<5,所以它符合奖金总数不超过5万元的要求.
再计算按模型y=log7x+1奖励时,奖金是否不超过利润的25%,即当
x∈[10,1 000]时,是否有
令y=log7x+1-0.25x,x∈[10,1 000].利用计算机作出函数f(x)的图象
(如图所示).由图象可知它是递减的,因此f(x)y=log7x+1<0.25x,
所以当x∈[10,1 000]时, <0.25.说明按模型y=log7x+1
时,奖金不会超过利润的25%.
课堂练习
1.存在x0,当x>x0时,下列不等式恒成立的是( )
A.2x2.某公司为了适应市场需求对产品结构作了重大调整,调整后初期利润增长迅速,后来 增长越来越慢,若要建立恰当的函数模型来反映该公司调整后利润y与时间x的关系,可选用( )
A.一次函数 B.幂函数 C.指数型函数 D.对数型函数
答案:D
解析:初期利润增长迅速,后来增长越来越慢.可用对数型函数模型来反映调整后利润与时间的关系.
答案:D
课堂总结
指数函数 对数函数 一元一次函数
解析式 y=ax(a>1) y=logax(a>1) y=kx(k>0)
单调性 在(0,+∞)上单调递增 图象 逐渐与y轴平行 逐渐与x轴平行 直线逐渐上升
增长速度 越来越快 越来越慢 增长速度不变
存在一个x0,当x>x0时,ax>kx>logax 三种函数的性质及增长速度比较
板书设计
指数函数
几类函数增长性差异比较
图像逐渐与y轴平行
增长速度越来越快
对数函数
图像逐渐与x轴平行
增长速度越来越慢
一元一次函数
图像直线逐渐上升
增长速度不变
y=ax(a>1)
y=logax(a>1)
y=kx(k>0)
存在一个x0,当x>x0时,ax>kx>logax
作业布置
3、课本P139练习1、2、3、4
1、在同一坐标系内作出函数y=2x,y=x2,y=log2x的图象并
探究它们的增长情况.
2、某公司为了实现1 000万元利润的目标,准备制定一个激励销售部门的
奖励方案:在销售利润达到10万元时, 按销售利润进行奖励,且奖金y(单
位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万
元,同时奖金总数不超过利润的25%.现有三个奖励方案模型:y=0.25x,
y=log7x+1,y=1.002x,其中哪个模型能符合该公司的要求
https://www.21cnjy.com/help/help_extract.php
4.4.3不同函数增长的差异
人教A(2019)版
必修一
新知导入
复习巩固
1、指数函数的图象和性质
a>1 0
R
(0,+∞)
(0,1)
增函数
减函数
非奇非偶
非奇非偶
(6)当x>0时,y>1.
当x<0时,0
x
y
o
1
x
y
o
1
对数函数的图象和性质
a>1 0
性 质 定义域: 值域:
在(0,+∞)上是 函数 在(0,+∞)上是 函数
(0,+∞)
过点(1,0),即当x=1时,y=0
增
减
0
>
y
新知导入
一次函数与指数函数的增长方式存在很大差异.事实上, 这种差异正是不同类型现实问题具有不同增长规律的反映.因此,如果把握了不同函数增长方式的差异,那么就可以根据现实问题的增长情况,选择合适的函数模型刻画其变化规律.下面就来研究一次函数、指数函数和对数函数增长方式的差异.
我们以y=2x和y=2x为例来探讨一下一次函数与指数函数增长的差异
新知讲解
在同一坐标系画出y=2x与y=2x的图像
可以看到,函数y=2x和y=2x的图象有两个交点(1,2),(2,4).在区间[0,1)上,函数y=2x的图象位于y=2x的图象之上,2x>2x;在区间(0,2)上,函数y=2x的图象位于y=2x的图象之下,2x <2x;在区间(2,3)上,函数y=2x的图象位于y=2x的图象之上,2x >2x.这表明,虽然这两个函数在[0,+∞)上都单调递增,但它们的增长速度不同,函数狔=2狓的增长速度保持不
变,而函数狔=2狓的增长速度在变化.
新知讲解
当自变量狓越来越大时,y=2x的图象就像与x轴垂直一样,2x的值快速增长;而函数y=2x的增长速度依然保持不变,与函数y=2x的增长速度相比几乎微不足道.
一般地,指数函数y=ax(a>1)与一次函数y=kx(k>0)的增长差异都与上述情况类似.即使k的值远远大于a的值,y=ax(a>1)的增长速度最终都会大大超过y=kx(k>0)的增长速度.
新知讲解
可以看到,虽然它们在[0,+∞)上都单调递增,但增长速度存在着明显的差异.函数 的增长速度保持不变,而y=lgx的增长速度在变化.随着狓的增大,函数 的图象离x轴越来越远,而函数y=lgx的图象越来越平缓,就像与x轴平行一样.
我们再来比较一次函数与对数函数的增长差异
我们以y=lgx和 为代表来考察这两类函数
新知讲解
一般地,虽然对数函数y=logax(a>1)与一次函数y=kx(k>0)在区间(0,+∞)上都单调递增,但它们的增长速度不同.随着x的增大,一次函数y=kx(k>0)保持固定的增长速度,而对数函数y=logax(a>1)的增长速度越来越慢.不论a的值比k的值大多少,在一定范围内,logax可能会大于kx,但由于logax的增长慢于kx的增长,因此总会存在一个x0,当x>x0时,恒有logax<kx.
新知讲解
指数函数 对数函数 一元一次函数
解析式 y=ax(a>1) y=logax(a>1) y=kx(k>0)
单调性 在(0,+∞)上单调递增 图象 逐渐与y轴平行 逐渐与x轴平行 直线逐渐上升
增长速度 越来越快 越来越慢 增长速度不变
存在一个x0,当x>x0时,ax>kx>logax 三种函数的性质及增长速度比较
新知讲解
合作探究
例1、 某公司为了实现1 000万元利润的目标,准备制定一个激励销售部门的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金总数不超过利润的25%.现有三个奖励方案模型:y=0.25x,y=log7x+1,y=1.002x,其中哪个模型能符合该公司的要求
分析:某个奖励模型符合公司要求,就是依据这个模型进行奖励时,奖金总数不超过5万元,同时奖金总数不超过利润的25%,由于公司总的利润目标为1 000万元,所以部门销售利润一般不会超过公司总的利润.
于是,只需在区间[10,1 000],分别检验三个模型是否符合公司要求.
合作探究
解:借助计算机作出函数y=5,y=0.25x,
y=log7x+1,y=1.002x在第一象限内
的大致图象(如图所示):
观察图象发现,在区间[10,1 000]上,模型y=0.25x,y=1.002x的图象都
有一部分在直线y=5的上方,只有模型y=log7x+1的图象始终在y=5的下方,
这说明只有按模型y=log2x+1进行奖励时才符合公司的要求,下面通过计算
确认上述判断.
对于模型y=0.25x,它在区间[10,1 000]上递增,当x∈(20,1 000)时,
y>5,因此该模型不符合要求;
合作探究
对于模型y=1.002x,由函数图象,并利用计算器,可知在区间(805,806)
内有一个点x0满足1.002x=5,由于它在区间[10,1 000]上递增,因此当x>x0时,
y>5,因此该模型y=1.002x也不符合要求;
对于模型y=log7x+1,它在区间[10,1000]上递增,而且当x=1000时,
y=log71 000+1≈4.55<5,所以它符合奖金总数不超过5万元的要求.
再计算按模型y=log7x+1奖励时,奖金是否不超过利润的25%,即当
x∈[10,1 000]时,是否有
令y=log7x+1-0.25x,x∈[10,1 000].利用计算机作出函数f(x)的图象
(如图所示).由图象可知它是递减的,因此f(x)
所以当x∈[10,1 000]时, <0.25.说明按模型y=log7x+1
时,奖金不会超过利润的25%.
课堂练习
1.存在x0,当x>x0时,下列不等式恒成立的是( )
A.2x
A.一次函数 B.幂函数 C.指数型函数 D.对数型函数
答案:D
解析:初期利润增长迅速,后来增长越来越慢.可用对数型函数模型来反映调整后利润与时间的关系.
答案:D
课堂总结
指数函数 对数函数 一元一次函数
解析式 y=ax(a>1) y=logax(a>1) y=kx(k>0)
单调性 在(0,+∞)上单调递增 图象 逐渐与y轴平行 逐渐与x轴平行 直线逐渐上升
增长速度 越来越快 越来越慢 增长速度不变
存在一个x0,当x>x0时,ax>kx>logax 三种函数的性质及增长速度比较
板书设计
指数函数
几类函数增长性差异比较
图像逐渐与y轴平行
增长速度越来越快
对数函数
图像逐渐与x轴平行
增长速度越来越慢
一元一次函数
图像直线逐渐上升
增长速度不变
y=ax(a>1)
y=logax(a>1)
y=kx(k>0)
存在一个x0,当x>x0时,ax>kx>logax
作业布置
3、课本P139练习1、2、3、4
1、在同一坐标系内作出函数y=2x,y=x2,y=log2x的图象并
探究它们的增长情况.
2、某公司为了实现1 000万元利润的目标,准备制定一个激励销售部门的
奖励方案:在销售利润达到10万元时, 按销售利润进行奖励,且奖金y(单
位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万
元,同时奖金总数不超过利润的25%.现有三个奖励方案模型:y=0.25x,
y=log7x+1,y=1.002x,其中哪个模型能符合该公司的要求
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
