2021-2022学年人教版数学八年级上册13.3.1.3等腰三角形的判定 课件(共16张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册13.3.1.3等腰三角形的判定 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 515.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
等腰三角形 的判定
1、等腰三角形的性质是什么?
(1)等腰三角形的两个底角相等。
(可以简称:等边对等角)
2 、等腰三角形的对称轴是什么?
(2)等腰三角形的顶角平分线与底边上的中线,底边上的高互相重合
(等腰三角形三线合一)
复习旧知
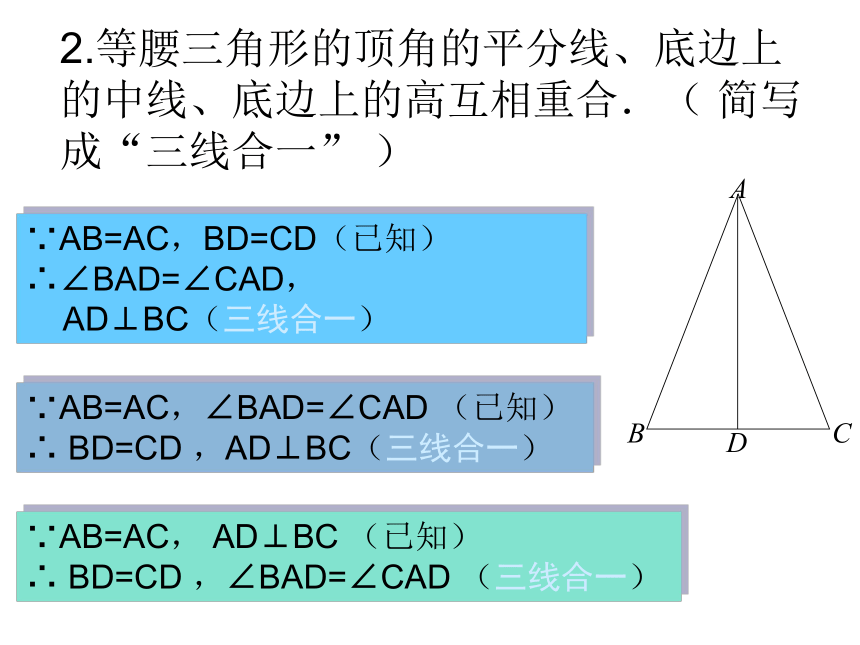
2.等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合.( 简写成“三线合一” )
A
B
C
D
∵AB=AC,BD=CD(已知)
∴∠BAD=∠CAD,
AD⊥BC(三线合一)
∵AB=AC,∠BAD=∠CAD (已知)
∴ BD=CD ,AD⊥BC(三线合一)
∵AB=AC, AD⊥BC (已知)
∴ BD=CD ,∠BAD=∠CAD (三线合一)
学习目标:
1、理解等腰三角形的判定方法及应用
2、会运用等腰三角形的判定方法和性质进行推理和运算
如果一个三角形有两个角相等,
那么这两个角所对的边也相等.
简写成”等角对等边”.
你能证明“等角对等边”吗?
提出猜想
已知:⊿ABC中,∠B=∠C
求证:AB=AC
证明:
作∠BAC的平分线AD
在⊿BAD和⊿CAD中,
∠1=∠2,
∠B=∠C,
AD=AD
∴ ⊿BAD≌ ⊿CAD(AAS)
∴AB=AC(全等三角形的对应边相等)
1
A
B
C
D
2
还有其他证法吗?
∵ AD平分∠BAC ,
∴ ∠ 1=∠2
如果一个三角形 有两个角相等,那么这两个角所对的边也相等.
注意: “等角对等边”的前提是一个 三角形
已知:在 △ ABC中, ∠B=∠C
求证:AB=AC
证明:
作BC边上的高AD
在 △ BAD和△ CAD中,
∠B=∠C
∴ △ BAD≌ △ CAD
∴AB=AC(全等三角形的对应边 相等)
A
B
C
D
∟
∠ADB=∠ADC=90 °
AD=AD
(AAS)
演绎推理 形成定理
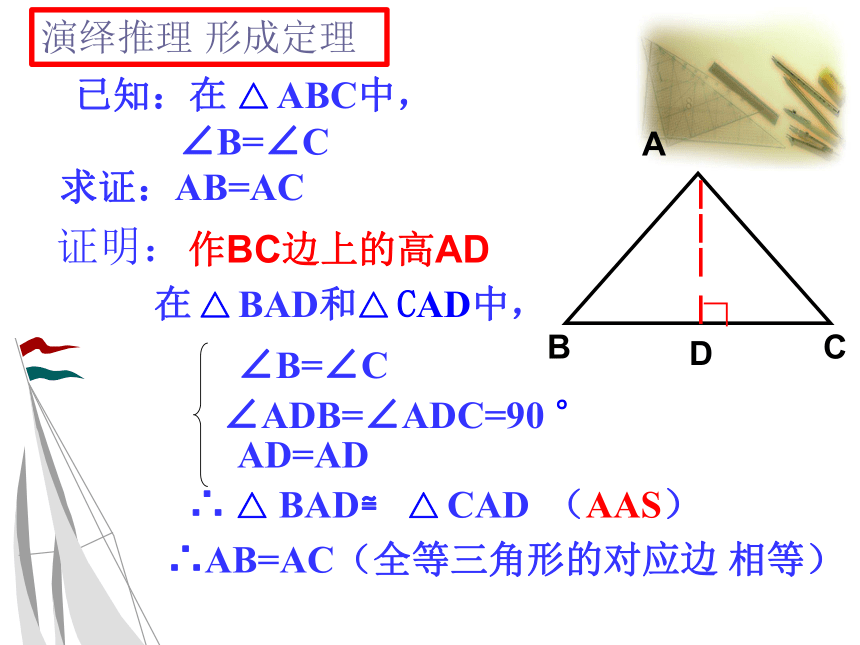
已知: △ ABC中,∠B=∠C
求证:AB=AC
证明:
作BC的中线AD
在△ BAD和△ CAD中,
BD=CD
AD=AD
∠B=∠C
∴ △ BAD和△ CAD不一定全等
∴AB和AC不一定相等
A
B
C
D
演绎推理 形成定理
如果一个三角形中有两个角相等,那么这两个 角所对的边也相等(简称“等角对等边”)
在 ABC中,
∵∠B=∠C
∴AB=AC
几何语言表示如下:
等腰三角形的判定定理
C
B
A
这又是一个判定两条线段相等根据之一。
点拨提示
总 结
等腰三角形的判定:
如果一个三角形中有两个角相等,那么这
两个角所对的边也相等.(简称为:等角对等边)
等腰三角形的性质与判定有区别吗
性质是:等边 等角
判定是:等角 等边
例1:求证:如果三角形一个外角的平分线平行于
三角形的一边,那么这个三角形是等腰三角形。
求证:△ABC是等腰三角形
如图,∠CAE是⊿ABC的外角,AD平分∠CAE , AD∥BC。
已知:
证明:
∵AD∥BC,
∴∠1=∠B(两直线平行,同位角相等)
∠2=∠C(两直线平行,内错角相等)
∵ AD平分∠CAE ∴ ∠1=∠2,
∴∠B=∠C,
∴ △ABC是等腰三角形。
A
B
C
D
E
1
2
综合运用
1、如图△ABC中,AB=AC,∠B=36°,D、E分别是BC边上两点,且∠ADE=∠AED=2∠BAD,则图中等腰三角形有( )个。
C
共有6个。
即△ABC、
△ ADE、
△ AEC、
△ ABD、
B
E
D
A
△ ABE。
△ ADC、
B
A
D
C
证明: ∵ AD ∥BC ∴∠ADB=∠DBC
∵ BD平分∠ABC ∴∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD (等角对等边)
已知:如图,
AD ∥BC,BD平分∠ABC。
求证:AB=AD
B
A
D
C
解答
练习1
2、如图,把一张矩形的纸沿对角线折叠,重合
的部分是一个等腰三角形吗?为什么?
A
B
C
G
D
E
1
2
3
解:重合部分是等腰三角形。
理由:由ABDC是矩形知
AC∥BD
∴∠ 3= ∠ 2
由沿对角线折叠知
∠ 1 = ∠ 2
∴ ∠ 1= ∠ 3
∴ BG=GC(等角对等边)
你的细心加你的
耐心等于成功!
如图:△ABC中,AB=AC,AD和BE是高,它们相交于点H,且AE=BE。 求证:AH=2BD
A
B
C
D
E
H
证明:∵AB=AC,AD是高,∴BC=2BD
⌒
1
⌒
2
又∵BE是高,∴∠ADC=∠BEC=∠AEH=90°
在△AEH和△BEC中
∴△AEH≌△BEC(ASA)
∴∠1+∠C=∠2+∠C=90°∴ ∠1=∠2
︸
∠AEH=∠BEC
AE=BE
∠1=∠2
∴AH=BC
∴AH=2BD
摩拳擦掌
课后思考
小结:
1、等腰三角形的判定定理是什么?
2、等腰三角形的判定方法有下列几种:
①定义 ②判定定理
3、等腰三角形的判定定理与性质定理
的区别是条件和结论刚好相反。
4、运用等腰三角形的判定定理时,
应注意在同一个三角形中
等腰三角形 的判定
1、等腰三角形的性质是什么?
(1)等腰三角形的两个底角相等。
(可以简称:等边对等角)
2 、等腰三角形的对称轴是什么?
(2)等腰三角形的顶角平分线与底边上的中线,底边上的高互相重合
(等腰三角形三线合一)
复习旧知
2.等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合.( 简写成“三线合一” )
A
B
C
D
∵AB=AC,BD=CD(已知)
∴∠BAD=∠CAD,
AD⊥BC(三线合一)
∵AB=AC,∠BAD=∠CAD (已知)
∴ BD=CD ,AD⊥BC(三线合一)
∵AB=AC, AD⊥BC (已知)
∴ BD=CD ,∠BAD=∠CAD (三线合一)
学习目标:
1、理解等腰三角形的判定方法及应用
2、会运用等腰三角形的判定方法和性质进行推理和运算
如果一个三角形有两个角相等,
那么这两个角所对的边也相等.
简写成”等角对等边”.
你能证明“等角对等边”吗?
提出猜想
已知:⊿ABC中,∠B=∠C
求证:AB=AC
证明:
作∠BAC的平分线AD
在⊿BAD和⊿CAD中,
∠1=∠2,
∠B=∠C,
AD=AD
∴ ⊿BAD≌ ⊿CAD(AAS)
∴AB=AC(全等三角形的对应边相等)
1
A
B
C
D
2
还有其他证法吗?
∵ AD平分∠BAC ,
∴ ∠ 1=∠2
如果一个三角形 有两个角相等,那么这两个角所对的边也相等.
注意: “等角对等边”的前提是一个 三角形
已知:在 △ ABC中, ∠B=∠C
求证:AB=AC
证明:
作BC边上的高AD
在 △ BAD和△ CAD中,
∠B=∠C
∴ △ BAD≌ △ CAD
∴AB=AC(全等三角形的对应边 相等)
A
B
C
D
∟
∠ADB=∠ADC=90 °
AD=AD
(AAS)
演绎推理 形成定理
已知: △ ABC中,∠B=∠C
求证:AB=AC
证明:
作BC的中线AD
在△ BAD和△ CAD中,
BD=CD
AD=AD
∠B=∠C
∴ △ BAD和△ CAD不一定全等
∴AB和AC不一定相等
A
B
C
D
演绎推理 形成定理
如果一个三角形中有两个角相等,那么这两个 角所对的边也相等(简称“等角对等边”)
在 ABC中,
∵∠B=∠C
∴AB=AC
几何语言表示如下:
等腰三角形的判定定理
C
B
A
这又是一个判定两条线段相等根据之一。
点拨提示
总 结
等腰三角形的判定:
如果一个三角形中有两个角相等,那么这
两个角所对的边也相等.(简称为:等角对等边)
等腰三角形的性质与判定有区别吗
性质是:等边 等角
判定是:等角 等边
例1:求证:如果三角形一个外角的平分线平行于
三角形的一边,那么这个三角形是等腰三角形。
求证:△ABC是等腰三角形
如图,∠CAE是⊿ABC的外角,AD平分∠CAE , AD∥BC。
已知:
证明:
∵AD∥BC,
∴∠1=∠B(两直线平行,同位角相等)
∠2=∠C(两直线平行,内错角相等)
∵ AD平分∠CAE ∴ ∠1=∠2,
∴∠B=∠C,
∴ △ABC是等腰三角形。
A
B
C
D
E
1
2
综合运用
1、如图△ABC中,AB=AC,∠B=36°,D、E分别是BC边上两点,且∠ADE=∠AED=2∠BAD,则图中等腰三角形有( )个。
C
共有6个。
即△ABC、
△ ADE、
△ AEC、
△ ABD、
B
E
D
A
△ ABE。
△ ADC、
B
A
D
C
证明: ∵ AD ∥BC ∴∠ADB=∠DBC
∵ BD平分∠ABC ∴∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD (等角对等边)
已知:如图,
AD ∥BC,BD平分∠ABC。
求证:AB=AD
B
A
D
C
解答
练习1
2、如图,把一张矩形的纸沿对角线折叠,重合
的部分是一个等腰三角形吗?为什么?
A
B
C
G
D
E
1
2
3
解:重合部分是等腰三角形。
理由:由ABDC是矩形知
AC∥BD
∴∠ 3= ∠ 2
由沿对角线折叠知
∠ 1 = ∠ 2
∴ ∠ 1= ∠ 3
∴ BG=GC(等角对等边)
你的细心加你的
耐心等于成功!
如图:△ABC中,AB=AC,AD和BE是高,它们相交于点H,且AE=BE。 求证:AH=2BD
A
B
C
D
E
H
证明:∵AB=AC,AD是高,∴BC=2BD
⌒
1
⌒
2
又∵BE是高,∴∠ADC=∠BEC=∠AEH=90°
在△AEH和△BEC中
∴△AEH≌△BEC(ASA)
∴∠1+∠C=∠2+∠C=90°∴ ∠1=∠2
︸
∠AEH=∠BEC
AE=BE
∠1=∠2
∴AH=BC
∴AH=2BD
摩拳擦掌
课后思考
小结:
1、等腰三角形的判定定理是什么?
2、等腰三角形的判定方法有下列几种:
①定义 ②判定定理
3、等腰三角形的判定定理与性质定理
的区别是条件和结论刚好相反。
4、运用等腰三角形的判定定理时,
应注意在同一个三角形中
