2021-2022学年青岛版数学九年级上册3.3《圆周角》同步练习卷 (Word版含答案)
文档属性
| 名称 | 2021-2022学年青岛版数学九年级上册3.3《圆周角》同步练习卷 (Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 209.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 13:15:57 | ||
图片预览



文档简介
2021年青岛版数学九年级上册
3.3《圆周角》同步练习卷
一、选择题
1.如图,⊙O是△ABC的外接圆,连接OA.OB,∠OBA=50°,则∠C的度数为( )
A.30° B.40° C.50° D.80°
2.如图,⊙O的直径AB=2,弦AC=1,点D在⊙O上,则∠D的度数是( )
A.30° B.45° C.60° D.75°
3.如图,在⊙O中,OD⊥BC,∠BOD=60°,则∠CAD的度数为( )
A.15° B.20° C.25° D.30°
4.从下列直角三角板与圆弧的位置关系中,可判断圆弧为半圆的是( )
5.如图,在⊙O中,若C是弧BD的中点,则图中与∠BAC相等的角有( )
A.1个 B.2 个 C.3个 D.4个
6.如图,点A,B,C,D都在⊙O上,AC,BD相交于点E,则∠ABD=( )
A.∠ACD B.∠ADB C.∠AED D.∠ACB
7.如图,在⊙O中,弦AB∥CD,若∠ABC=40°,则∠BOD=( )
A.20° B.40° C.50° D.80°
8.如图,在⊙O中,若C是的中点,则图中与∠BAC相等的角有( )
A.1个 B.2个 C.3个 D.4个
9.如图,已知点C,D是半圆上三等分点,连接AC,BC,CD,OD,BC和OD相交于点E.
则下列结论:①∠CBA=30°,②OD⊥BC,③2OE=AC,④四边形AODC是菱形.
正确的个数是( )
A.1 B.2 C.3 D.4
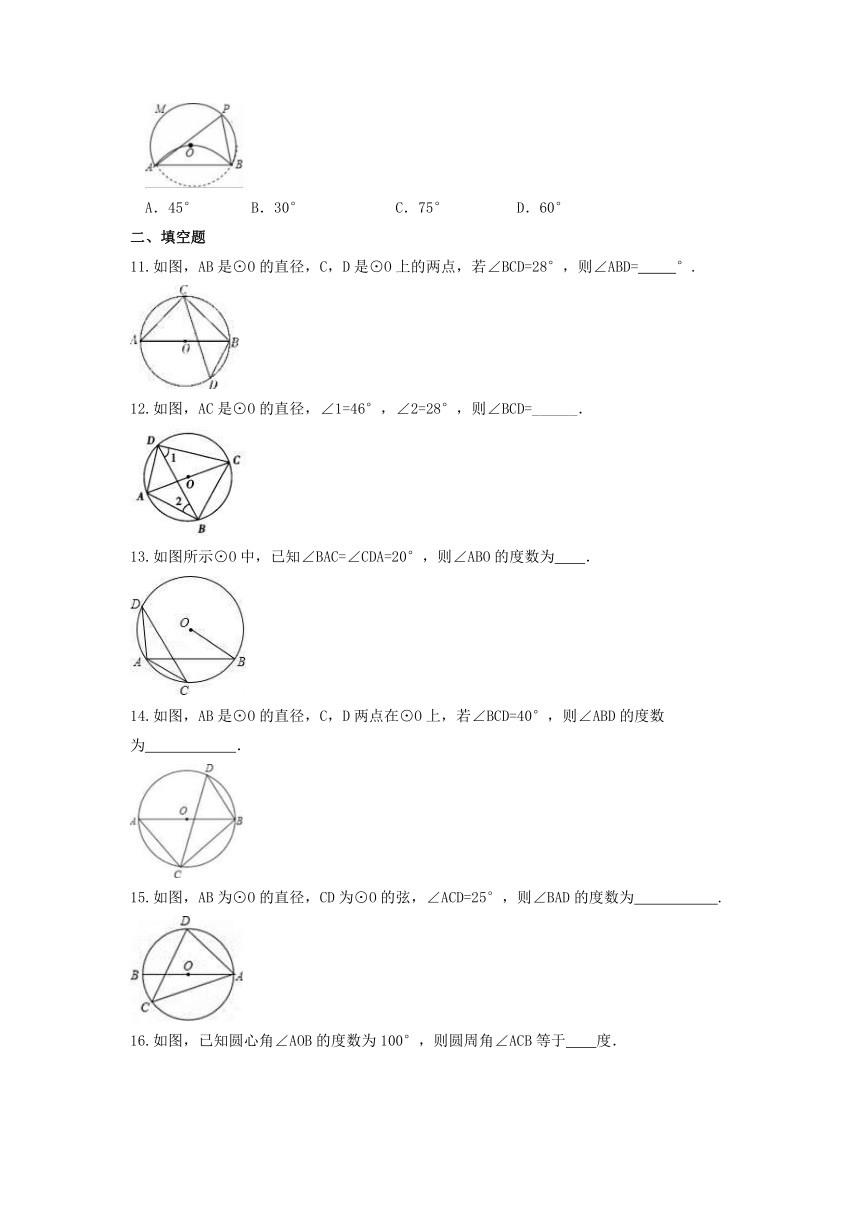
10.如图,将⊙O沿弦AB折叠,圆弧恰好经过圆心O,点P是优弧AMB上一点,则∠APB的度数为( )
A.45° B.30° C.75° D.60°
二、填空题
11.如图,AB是⊙O的直径,C,D是⊙O上的两点,若∠BCD=28°,则∠ABD= °.
12.如图,AC是⊙O的直径,∠1=46°,∠2=28°,则∠BCD=______.
13.如图所示⊙O中,已知∠BAC=∠CDA=20°,则∠ABO的度数为 .
14.如图,AB是⊙O的直径,C,D两点在⊙O上,若∠BCD=40°,则∠ABD的度数为 .
15.如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=25°,则∠BAD的度数为 .
16.如图,已知圆心角∠AOB的度数为100°,则圆周角∠ACB等于 度.
三、解答题
17.如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB平分线交⊙O于D,求BC,AD,BD的长.
18.如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.
19.如图,C,D两点在以AB为直径的半圆O上,AD平分∠BAC,AB=20,AD=4,DE⊥AB于E.
(1)求DE的长;
(2)求证:AC=2OE.
20.如图,A、B是⊙O上的两个点,已知P为平面内一点,(P、A、B三点不在同一条直线上).
(1)若点P在⊙O上,⊙O的半径为1.
①当∠APB=45°时,AB的长度为 ,
②当AB=1时,∠APB= °;
(2)若点P不在⊙O上,直线PA、PB交⊙O于点C、D(点C与点A、点D与点B均不重合),连接AD,设∠CAD=α,∠ADB=β,试用α、β表示∠APB(请直接写出答案,并画出示意图).
参考答案
1.B
2.C
3.D
4.B
5.C
6.A
7.D
8.C.
9.D;
10.D
11.答案为:62;
12.答案为:72°
13.答案为:50°
14.答案为:50°.
15.答案为:65°;
16.答案为:130.
17.解:∵AB是直径
∴∠ACB=∠ADB=90°
在Rt△ABC中,AB2=AC2+BC2,AB=10cm,AC=6cm
∴BC2=AB2﹣AC2=102﹣62=64
∴BC==8(cm)
又CD平分∠ACB,
∴∠ACD=∠BCD,
∴
∴AD=BD
又在Rt△ABD中,AD2+BD2=AB2
∴AD2+BD2=102
∴AD=BD==5(cm).
18.证明:(1)∵AB是直径,
∴∠AEB=90°,
∴AE⊥BC,
∵AB=AC,
∴BE=CE,
∵AE=EF,
∴四边形ABFC是平行四边形,
∵AC=AB,
∴四边形ABFC是菱形.
(2)设CD=x.连接BD.
∵AB是直径,
∴∠ADB=∠BDC=90°,
∴AB2﹣AD2=CB2﹣CD2,
∴(7+x)2﹣72=42﹣x2,解得x=1或﹣8(舍弃)
∴AC=8,BD==,
∴S菱形ABFC=8.
∴S半圆= π 42=8π.
19.(1)解:连接BD,∵AB为直径,
∴∠ADB=90°,
在Rt△ADB中,BD===4,
∵S△ADB=AD·BD=AB·DE,
∴AD·BD=AB·DE,
∴DE===4,即DE=4;
(2)证明:连接OD,作OF⊥AC于点F.
∵OF⊥AC,∴AC=2AF,
∵AD平分∠BAC,∴∠BAC=2∠BAD,
又∵∠BOD=2∠BAD,∴∠BAC=∠BOD,
Rt△OED和Rt△AFO中,
∵
∴△AFO≌△OED,
∴AF=OE,
∵AC=2AF,
∴AC=2OE.
20.解:(1)①∵点P在⊙O上,∠APB=45°,∴∠AOB=90°,
∵OA=OB=1,∴AB=;
②∵AB=1,OA=OB=1,∴△OAB是等边三角新,∴∠AOB=90°,
若点P在优弧上,则∠APB=30°,
若点P在劣弧上,则∠APB=180°﹣30°=150°;
综上可得:∠APB=30°或150°;故答案为:①;②30°或150°;
(2)①P在圆外时,
如图①,若点C、D分别在线段PA、PB上,则∠APB=β﹣α;
如图②,若点C在线段PA的延长线上,点D在线段PB上,则∠APB=α+β﹣180°;
如图③,若点C在线段PA上,点D在线段PB的延长线上,则∠APB=180°﹣α﹣β;
如图④,若点C、D分别在线段PA、PB的延长线上,则∠APB=α﹣β;
②P在圆内时,如图⑤,∠APB=α+β.
3.3《圆周角》同步练习卷
一、选择题
1.如图,⊙O是△ABC的外接圆,连接OA.OB,∠OBA=50°,则∠C的度数为( )
A.30° B.40° C.50° D.80°
2.如图,⊙O的直径AB=2,弦AC=1,点D在⊙O上,则∠D的度数是( )
A.30° B.45° C.60° D.75°
3.如图,在⊙O中,OD⊥BC,∠BOD=60°,则∠CAD的度数为( )
A.15° B.20° C.25° D.30°
4.从下列直角三角板与圆弧的位置关系中,可判断圆弧为半圆的是( )
5.如图,在⊙O中,若C是弧BD的中点,则图中与∠BAC相等的角有( )
A.1个 B.2 个 C.3个 D.4个
6.如图,点A,B,C,D都在⊙O上,AC,BD相交于点E,则∠ABD=( )
A.∠ACD B.∠ADB C.∠AED D.∠ACB
7.如图,在⊙O中,弦AB∥CD,若∠ABC=40°,则∠BOD=( )
A.20° B.40° C.50° D.80°
8.如图,在⊙O中,若C是的中点,则图中与∠BAC相等的角有( )
A.1个 B.2个 C.3个 D.4个
9.如图,已知点C,D是半圆上三等分点,连接AC,BC,CD,OD,BC和OD相交于点E.
则下列结论:①∠CBA=30°,②OD⊥BC,③2OE=AC,④四边形AODC是菱形.
正确的个数是( )
A.1 B.2 C.3 D.4
10.如图,将⊙O沿弦AB折叠,圆弧恰好经过圆心O,点P是优弧AMB上一点,则∠APB的度数为( )
A.45° B.30° C.75° D.60°
二、填空题
11.如图,AB是⊙O的直径,C,D是⊙O上的两点,若∠BCD=28°,则∠ABD= °.
12.如图,AC是⊙O的直径,∠1=46°,∠2=28°,则∠BCD=______.
13.如图所示⊙O中,已知∠BAC=∠CDA=20°,则∠ABO的度数为 .
14.如图,AB是⊙O的直径,C,D两点在⊙O上,若∠BCD=40°,则∠ABD的度数为 .
15.如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=25°,则∠BAD的度数为 .
16.如图,已知圆心角∠AOB的度数为100°,则圆周角∠ACB等于 度.
三、解答题
17.如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB平分线交⊙O于D,求BC,AD,BD的长.
18.如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.
19.如图,C,D两点在以AB为直径的半圆O上,AD平分∠BAC,AB=20,AD=4,DE⊥AB于E.
(1)求DE的长;
(2)求证:AC=2OE.
20.如图,A、B是⊙O上的两个点,已知P为平面内一点,(P、A、B三点不在同一条直线上).
(1)若点P在⊙O上,⊙O的半径为1.
①当∠APB=45°时,AB的长度为 ,
②当AB=1时,∠APB= °;
(2)若点P不在⊙O上,直线PA、PB交⊙O于点C、D(点C与点A、点D与点B均不重合),连接AD,设∠CAD=α,∠ADB=β,试用α、β表示∠APB(请直接写出答案,并画出示意图).
参考答案
1.B
2.C
3.D
4.B
5.C
6.A
7.D
8.C.
9.D;
10.D
11.答案为:62;
12.答案为:72°
13.答案为:50°
14.答案为:50°.
15.答案为:65°;
16.答案为:130.
17.解:∵AB是直径
∴∠ACB=∠ADB=90°
在Rt△ABC中,AB2=AC2+BC2,AB=10cm,AC=6cm
∴BC2=AB2﹣AC2=102﹣62=64
∴BC==8(cm)
又CD平分∠ACB,
∴∠ACD=∠BCD,
∴
∴AD=BD
又在Rt△ABD中,AD2+BD2=AB2
∴AD2+BD2=102
∴AD=BD==5(cm).
18.证明:(1)∵AB是直径,
∴∠AEB=90°,
∴AE⊥BC,
∵AB=AC,
∴BE=CE,
∵AE=EF,
∴四边形ABFC是平行四边形,
∵AC=AB,
∴四边形ABFC是菱形.
(2)设CD=x.连接BD.
∵AB是直径,
∴∠ADB=∠BDC=90°,
∴AB2﹣AD2=CB2﹣CD2,
∴(7+x)2﹣72=42﹣x2,解得x=1或﹣8(舍弃)
∴AC=8,BD==,
∴S菱形ABFC=8.
∴S半圆= π 42=8π.
19.(1)解:连接BD,∵AB为直径,
∴∠ADB=90°,
在Rt△ADB中,BD===4,
∵S△ADB=AD·BD=AB·DE,
∴AD·BD=AB·DE,
∴DE===4,即DE=4;
(2)证明:连接OD,作OF⊥AC于点F.
∵OF⊥AC,∴AC=2AF,
∵AD平分∠BAC,∴∠BAC=2∠BAD,
又∵∠BOD=2∠BAD,∴∠BAC=∠BOD,
Rt△OED和Rt△AFO中,
∵
∴△AFO≌△OED,
∴AF=OE,
∵AC=2AF,
∴AC=2OE.
20.解:(1)①∵点P在⊙O上,∠APB=45°,∴∠AOB=90°,
∵OA=OB=1,∴AB=;
②∵AB=1,OA=OB=1,∴△OAB是等边三角新,∴∠AOB=90°,
若点P在优弧上,则∠APB=30°,
若点P在劣弧上,则∠APB=180°﹣30°=150°;
综上可得:∠APB=30°或150°;故答案为:①;②30°或150°;
(2)①P在圆外时,
如图①,若点C、D分别在线段PA、PB上,则∠APB=β﹣α;
如图②,若点C在线段PA的延长线上,点D在线段PB上,则∠APB=α+β﹣180°;
如图③,若点C在线段PA上,点D在线段PB的延长线上,则∠APB=180°﹣α﹣β;
如图④,若点C、D分别在线段PA、PB的延长线上,则∠APB=α﹣β;
②P在圆内时,如图⑤,∠APB=α+β.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
