山东省泰安市新泰市2021-2022学年八年级上学期期中数学试题(word版含答案)
文档属性
| 名称 | 山东省泰安市新泰市2021-2022学年八年级上学期期中数学试题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 815.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 17:56:44 | ||
图片预览


文档简介
八年级上学期期中检测
数学试题
第Ⅰ卷(选择题共48分)
一、选择题(本大题共12小题,在每小题给出的选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得4分,选错、不选或选出的答案超过一个,均记零分)
1.下列由左边到右边的变形,属于因式分解的是()
A. B.
C. D.
2.下列各式,,,,,,,其中是分式的有()
A.2个 B.3个 C.4个 D.5个
3.若把分式中的a、b都缩小为原来的,则分式的值()
A.缩小为原来的 B.扩大为原来的6倍 C.缩小为原来的 D.不变
4.已知一组数据:2,0,,4,2,.这组数据的众数和中位数分别是()
A.2,1.5 B.2,-1 C.2,1 D.2,2
5.如果分式的值为,则x的值为()
A. B.2 C. D.0
6.为有效解决交通拥堵问题,营造路网微循环,某市决定对一条长的道路进行改造拓宽,为了尽量减轻施工对城市交通造成的影响,实际施工时,每天改造道路的长度比原计划增加10%,结果提前6天完成任务,求实际每天改造道路的长度与实际施工天数,嘉琪同学根据题意列出方程,则方程中未知数x所表示的量是()
A.实际每天改造道路的长度 B.原计划每大改造道路的长度
C.原计划施工的天数 D.实际施工的天数
7.已知,则的值为()
A.4 B.2 C. D.
8.数据2,5,5,7,x,3的平均数是4,则中位数是()
A.6 B.5 C.4.5 D.4
9.若化简的结果为,则“□”是()
A. B. C.a D.b
10.如图所示,边长为a,b的长方形的周长为14,面积为10,则的值为()
A.35 B.70 C.140 D.290
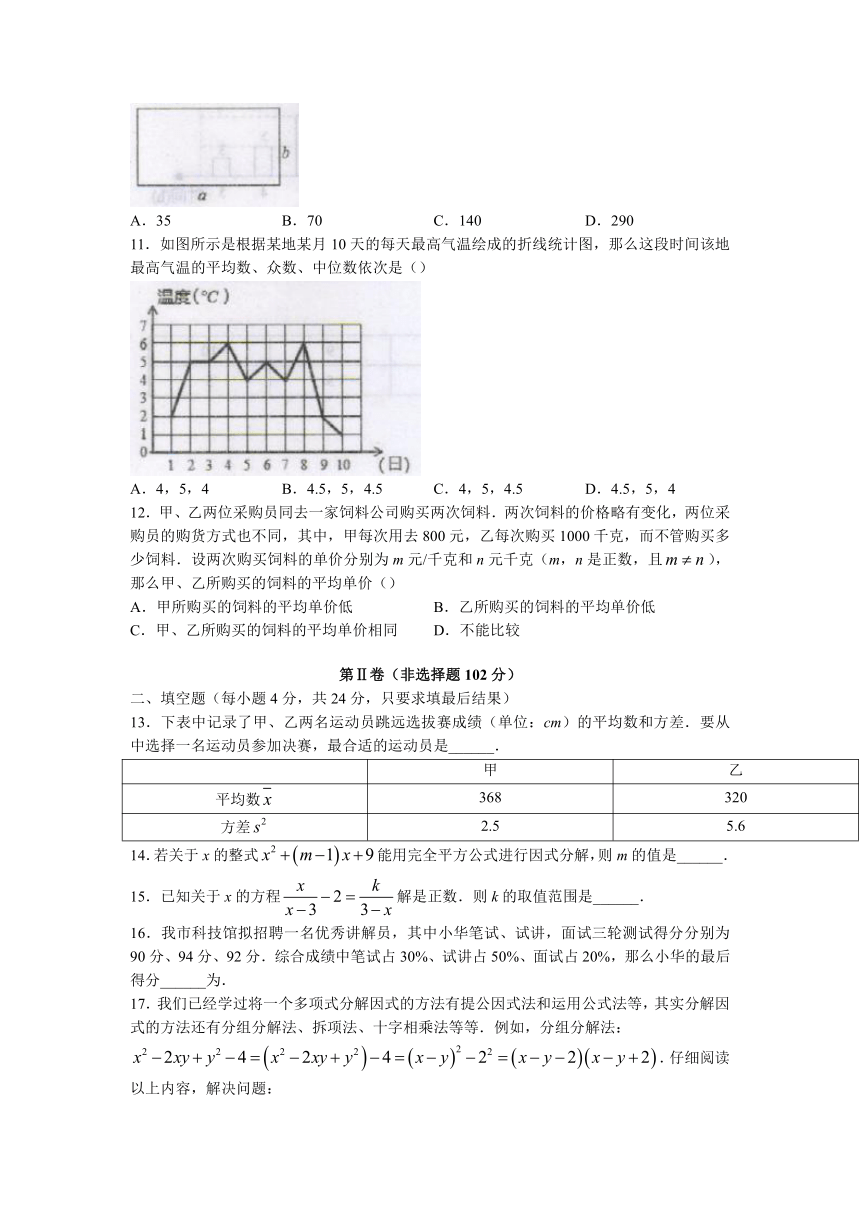
11.如图所示是根据某地某月10天的每天最高气温绘成的折线统计图,那么这段时间该地最高气温的平均数、众数、中位数依次是()
A.4,5,4 B.4.5,5,4.5 C.4,5,4.5 D.4.5,5,4
12.甲、乙两位采购员同去一家饲料公司购买两次饲料.两次饲料的价格略有变化,两位采购员的购货方式也不同,其中,甲每次用去800元,乙每次购买1000千克,而不管购买多少饲料.设两次购买饲料的单价分别为m元/千克和n元千克(m,n是正数,且),那么甲、乙所购买的饲料的平均单价()
A.甲所购买的饲料的平均单价低 B.乙所购买的饲料的平均单价低
C.甲、乙所购买的饲料的平均单价相同 D.不能比较
第Ⅱ卷(非选择题102分)
二、填空题(每小题4分,共24分,只要求填最后结果)
13.下表中记录了甲、乙两名运动员跳远选拔赛成绩(单位:cm)的平均数和方差.要从中选择一名运动员参加决赛,最合适的运动员是______.
甲 乙
平均数 368 320
方差 2.5 5.6
14.若关于x的整式能用完全平方公式进行因式分解,则m的值是______.
15.已知关于x的方程解是正数.则k的取值范围是______.
16.我市科技馆拟招聘一名优秀讲解员,其中小华笔试、试讲,面试三轮测试得分分别为90分、94分、92分.综合成绩中笔试占30%、试讲占50%、面试占20%,那么小华的最后得分______为.
17.我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法等,其实分解因式的方法还有分组分解法、拆项法、十字相乘法等等.例如,分组分解法:
.仔细阅读以上内容,解决问题:
已知:a、b、c为的三条边,,则的周长______.
18.已知关于x的分式方程,若这个方程无解,则m的值为______.
三、解答题(本题共7个小题,共78分,解答题写出文字说明、证明过程或推演步骤)
19.(10分)因式分解:
(1);
(2).
20.(10分)解答下列各题:
(1)计算:;
(2)先化简,再求值:,请从不等式组的整数解中选择一个合适的值代入求值.
21.(10分)解下列方程:
(1); (2).
22.(12分)提出问题:你能把多项式因式分解吗?
探究问题:如图1所示,设a,b为常数,由面积相等可得:
,将该式从右到左使用,就可以对形如的多项式进行因式分解即.观察多项式的特征是二次项系数为1,常数项为两数之积,一次项为两数之和.
解决问题:.
运用结论:
(1)基础运用:把多项式进行因式分解.
(2)知识迁移:对于多项式进行因式分解还可以这样思考:
将二次项分解成如图2所示中的两个的积,再将常数项分解成与3的乘积,图中的对角线上的乘积的和为,就是的一次项,所以有.这种分解因式的方法叫做“十字相乘法”.
请用十字相乘法进行因式分解:①;②.
23.(12分)某中学在创建“书香校园”活动中,为了解学生的读书情况,抽样调查了部分同学在一周内的阅读时间,绘制如图的统计图,根据图中提供信息,解答下列问题:
(1)被抽查学生阅读时间的中位数是______,众数是______,平均数是______;
(2)若该校共有学生2000人,请估算该校一周内阅读时间不少于的学生人数.
24.(12分)某学校从九年级同学中任意选取40人,随机分成甲、乙两个小组进行“引体向上”体能测试,根据测试成绩绘制出统计表和如图所示的统计图(成绩均为整数,满分为10分)
甲组成绩统计表:
成绩 7 8 9 10
人数 1 9 5 5
乙组成绩统计图
根据上面的信息,解答下列问题:
(1)甲组的平均成绩为______分,______,甲组成绩的中位数是______,乙组成绩的众数是______;
(2)若已经计算出甲组成绩方差为0.81,求出乙组成绩的方差,并判断哪个小组的成绩更加稳定?
25.(12分)受疫情影响,洗手液需求量猛增,某商场用4000元购进一批洗手液后,供不应求,商场用8800元购进第二批这种洗手液,所购数量是第一批数量的2倍,但单价贵了1元.
(1)求该商场购进的第一批洗手液的单价;
(2)商场销售这种洗手液时,每瓶定价为13元,最后200瓶按9折销售,很快售完,在这两笔生意中商场共获利多少元?
九年级上学期期中检测数学答案
一、选择题
DDBDC DDBAA BA
二、填空题
13、 14、且 15、 16、12 17、6 18、①③④
三、解答题
19、(1)
(2)
20、(1)∵新坡面的坡度为,∴,
∴.答:新坡面的坡角为30°.
(2)文化墙PM不需要拆除.过点C作于点D,则,
∵坡面BC的坡度为1:1,新坡面的坡度为,∴,,
∴,∴文化墙PM不需要拆除.
21、解:(1).
(2)由题意得,解得,(不符合题意,舍去).
∴x的值为10.
.最大为.
22、解:(1)设直线与y轴交于点D,
在中,,.
∴,即点,把点,代入直线得,,,
解得,,∴直线的关系式为;
把,代入得,
,,∴,,
∴,∴反比例函数的关系式为,
因此,;
(2)由,,.
(3)由图象可知,当时,不等式的解集为.
23、解:(1)设当时,反比例函数的解析式为,
将代入得:,解得,
∴反比例函数的解析式为,当时,
,∴,∴,
即A对应的指标值为20;
(2)设当时,AB的解析式为,
将、代入得:,
解得,∴AB的解析式为,
当时,,解得,
由(1)得反比例函数的解析式为,
当时,,解得,
∴时,注意力指标都不低于36,
而,
∴张老师能经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于36.
24、解:(1)根据题意得,;
(2)根据题意得,,
解得:,,∵每件利润不能超过60元,∴.
答:当x为10时,超市每天销售这种玩具可获利润2250元;
(3)根据题意得,,
∵,∴当时,w随x的增大而增大,
∵,,∴当时,,
答:当x为20时w最大,最大值是2400元.
25、解:(1)将,代入得,
,解得:,
∴二次函数的表达式为.
(2)当时,,∴,∴,∵,,∴,,
∴,
∵,,
∴,∴,∵点P在x轴上方,
∴,∴,解得:(舍)或,∴点P的坐标为.
(3)设直线BC的解析式为,则
,解得:,
∴直线BC的解析式为,
设点,则,
∵点D在线段BC上,∴点E在点D的上方,
∴,
∴当时,.
∴当DE取得最大值时,四边形OBCE的面积有最大值.
,此时,点E的坐标为.
数学试题
第Ⅰ卷(选择题共48分)
一、选择题(本大题共12小题,在每小题给出的选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得4分,选错、不选或选出的答案超过一个,均记零分)
1.下列由左边到右边的变形,属于因式分解的是()
A. B.
C. D.
2.下列各式,,,,,,,其中是分式的有()
A.2个 B.3个 C.4个 D.5个
3.若把分式中的a、b都缩小为原来的,则分式的值()
A.缩小为原来的 B.扩大为原来的6倍 C.缩小为原来的 D.不变
4.已知一组数据:2,0,,4,2,.这组数据的众数和中位数分别是()
A.2,1.5 B.2,-1 C.2,1 D.2,2
5.如果分式的值为,则x的值为()
A. B.2 C. D.0
6.为有效解决交通拥堵问题,营造路网微循环,某市决定对一条长的道路进行改造拓宽,为了尽量减轻施工对城市交通造成的影响,实际施工时,每天改造道路的长度比原计划增加10%,结果提前6天完成任务,求实际每天改造道路的长度与实际施工天数,嘉琪同学根据题意列出方程,则方程中未知数x所表示的量是()
A.实际每天改造道路的长度 B.原计划每大改造道路的长度
C.原计划施工的天数 D.实际施工的天数
7.已知,则的值为()
A.4 B.2 C. D.
8.数据2,5,5,7,x,3的平均数是4,则中位数是()
A.6 B.5 C.4.5 D.4
9.若化简的结果为,则“□”是()
A. B. C.a D.b
10.如图所示,边长为a,b的长方形的周长为14,面积为10,则的值为()
A.35 B.70 C.140 D.290
11.如图所示是根据某地某月10天的每天最高气温绘成的折线统计图,那么这段时间该地最高气温的平均数、众数、中位数依次是()
A.4,5,4 B.4.5,5,4.5 C.4,5,4.5 D.4.5,5,4
12.甲、乙两位采购员同去一家饲料公司购买两次饲料.两次饲料的价格略有变化,两位采购员的购货方式也不同,其中,甲每次用去800元,乙每次购买1000千克,而不管购买多少饲料.设两次购买饲料的单价分别为m元/千克和n元千克(m,n是正数,且),那么甲、乙所购买的饲料的平均单价()
A.甲所购买的饲料的平均单价低 B.乙所购买的饲料的平均单价低
C.甲、乙所购买的饲料的平均单价相同 D.不能比较
第Ⅱ卷(非选择题102分)
二、填空题(每小题4分,共24分,只要求填最后结果)
13.下表中记录了甲、乙两名运动员跳远选拔赛成绩(单位:cm)的平均数和方差.要从中选择一名运动员参加决赛,最合适的运动员是______.
甲 乙
平均数 368 320
方差 2.5 5.6
14.若关于x的整式能用完全平方公式进行因式分解,则m的值是______.
15.已知关于x的方程解是正数.则k的取值范围是______.
16.我市科技馆拟招聘一名优秀讲解员,其中小华笔试、试讲,面试三轮测试得分分别为90分、94分、92分.综合成绩中笔试占30%、试讲占50%、面试占20%,那么小华的最后得分______为.
17.我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法等,其实分解因式的方法还有分组分解法、拆项法、十字相乘法等等.例如,分组分解法:
.仔细阅读以上内容,解决问题:
已知:a、b、c为的三条边,,则的周长______.
18.已知关于x的分式方程,若这个方程无解,则m的值为______.
三、解答题(本题共7个小题,共78分,解答题写出文字说明、证明过程或推演步骤)
19.(10分)因式分解:
(1);
(2).
20.(10分)解答下列各题:
(1)计算:;
(2)先化简,再求值:,请从不等式组的整数解中选择一个合适的值代入求值.
21.(10分)解下列方程:
(1); (2).
22.(12分)提出问题:你能把多项式因式分解吗?
探究问题:如图1所示,设a,b为常数,由面积相等可得:
,将该式从右到左使用,就可以对形如的多项式进行因式分解即.观察多项式的特征是二次项系数为1,常数项为两数之积,一次项为两数之和.
解决问题:.
运用结论:
(1)基础运用:把多项式进行因式分解.
(2)知识迁移:对于多项式进行因式分解还可以这样思考:
将二次项分解成如图2所示中的两个的积,再将常数项分解成与3的乘积,图中的对角线上的乘积的和为,就是的一次项,所以有.这种分解因式的方法叫做“十字相乘法”.
请用十字相乘法进行因式分解:①;②.
23.(12分)某中学在创建“书香校园”活动中,为了解学生的读书情况,抽样调查了部分同学在一周内的阅读时间,绘制如图的统计图,根据图中提供信息,解答下列问题:
(1)被抽查学生阅读时间的中位数是______,众数是______,平均数是______;
(2)若该校共有学生2000人,请估算该校一周内阅读时间不少于的学生人数.
24.(12分)某学校从九年级同学中任意选取40人,随机分成甲、乙两个小组进行“引体向上”体能测试,根据测试成绩绘制出统计表和如图所示的统计图(成绩均为整数,满分为10分)
甲组成绩统计表:
成绩 7 8 9 10
人数 1 9 5 5
乙组成绩统计图
根据上面的信息,解答下列问题:
(1)甲组的平均成绩为______分,______,甲组成绩的中位数是______,乙组成绩的众数是______;
(2)若已经计算出甲组成绩方差为0.81,求出乙组成绩的方差,并判断哪个小组的成绩更加稳定?
25.(12分)受疫情影响,洗手液需求量猛增,某商场用4000元购进一批洗手液后,供不应求,商场用8800元购进第二批这种洗手液,所购数量是第一批数量的2倍,但单价贵了1元.
(1)求该商场购进的第一批洗手液的单价;
(2)商场销售这种洗手液时,每瓶定价为13元,最后200瓶按9折销售,很快售完,在这两笔生意中商场共获利多少元?
九年级上学期期中检测数学答案
一、选择题
DDBDC DDBAA BA
二、填空题
13、 14、且 15、 16、12 17、6 18、①③④
三、解答题
19、(1)
(2)
20、(1)∵新坡面的坡度为,∴,
∴.答:新坡面的坡角为30°.
(2)文化墙PM不需要拆除.过点C作于点D,则,
∵坡面BC的坡度为1:1,新坡面的坡度为,∴,,
∴,∴文化墙PM不需要拆除.
21、解:(1).
(2)由题意得,解得,(不符合题意,舍去).
∴x的值为10.
.最大为.
22、解:(1)设直线与y轴交于点D,
在中,,.
∴,即点,把点,代入直线得,,,
解得,,∴直线的关系式为;
把,代入得,
,,∴,,
∴,∴反比例函数的关系式为,
因此,;
(2)由,,.
(3)由图象可知,当时,不等式的解集为.
23、解:(1)设当时,反比例函数的解析式为,
将代入得:,解得,
∴反比例函数的解析式为,当时,
,∴,∴,
即A对应的指标值为20;
(2)设当时,AB的解析式为,
将、代入得:,
解得,∴AB的解析式为,
当时,,解得,
由(1)得反比例函数的解析式为,
当时,,解得,
∴时,注意力指标都不低于36,
而,
∴张老师能经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于36.
24、解:(1)根据题意得,;
(2)根据题意得,,
解得:,,∵每件利润不能超过60元,∴.
答:当x为10时,超市每天销售这种玩具可获利润2250元;
(3)根据题意得,,
∵,∴当时,w随x的增大而增大,
∵,,∴当时,,
答:当x为20时w最大,最大值是2400元.
25、解:(1)将,代入得,
,解得:,
∴二次函数的表达式为.
(2)当时,,∴,∴,∵,,∴,,
∴,
∵,,
∴,∴,∵点P在x轴上方,
∴,∴,解得:(舍)或,∴点P的坐标为.
(3)设直线BC的解析式为,则
,解得:,
∴直线BC的解析式为,
设点,则,
∵点D在线段BC上,∴点E在点D的上方,
∴,
∴当时,.
∴当DE取得最大值时,四边形OBCE的面积有最大值.
,此时,点E的坐标为.
同课章节目录
