2021-2022学年沪科版九年级数学上册23.2.3 解直角三角形 的应用问题 同步测试卷 (Word版含答案)
文档属性
| 名称 | 2021-2022学年沪科版九年级数学上册23.2.3 解直角三角形 的应用问题 同步测试卷 (Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 303.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 00:00:00 | ||
图片预览


文档简介
23.2.3 利用解直角三角形解视角中的应用问题同步测试卷 2021-2022学年度沪科版九年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共5小题,共25分)
如图,一棵大树被台风拦腰刮断,树根A到刮断点P的长度是4米,折断部分PB与地面成40°的夹角,那么原来树的长度是( )米.
A. B. C. D.
秀秀和山山在水平的地面上放风筝,某一时刻两人的风筝正好都停在对方的正上方,即此时AC⊥AB,DB⊥AB,两人之间的距离AB为120米,若两人的风筝线与水平线的夹角分别为α和β,则两人放出的风筝线AD与BC的长度和为(忽略两人的身高与手臂长度)( )米
A. B.
C. D.
如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底点G为BC的中点,则矮建筑物的高CD为( )
A. 米 B. 米 C. 米 D. 米
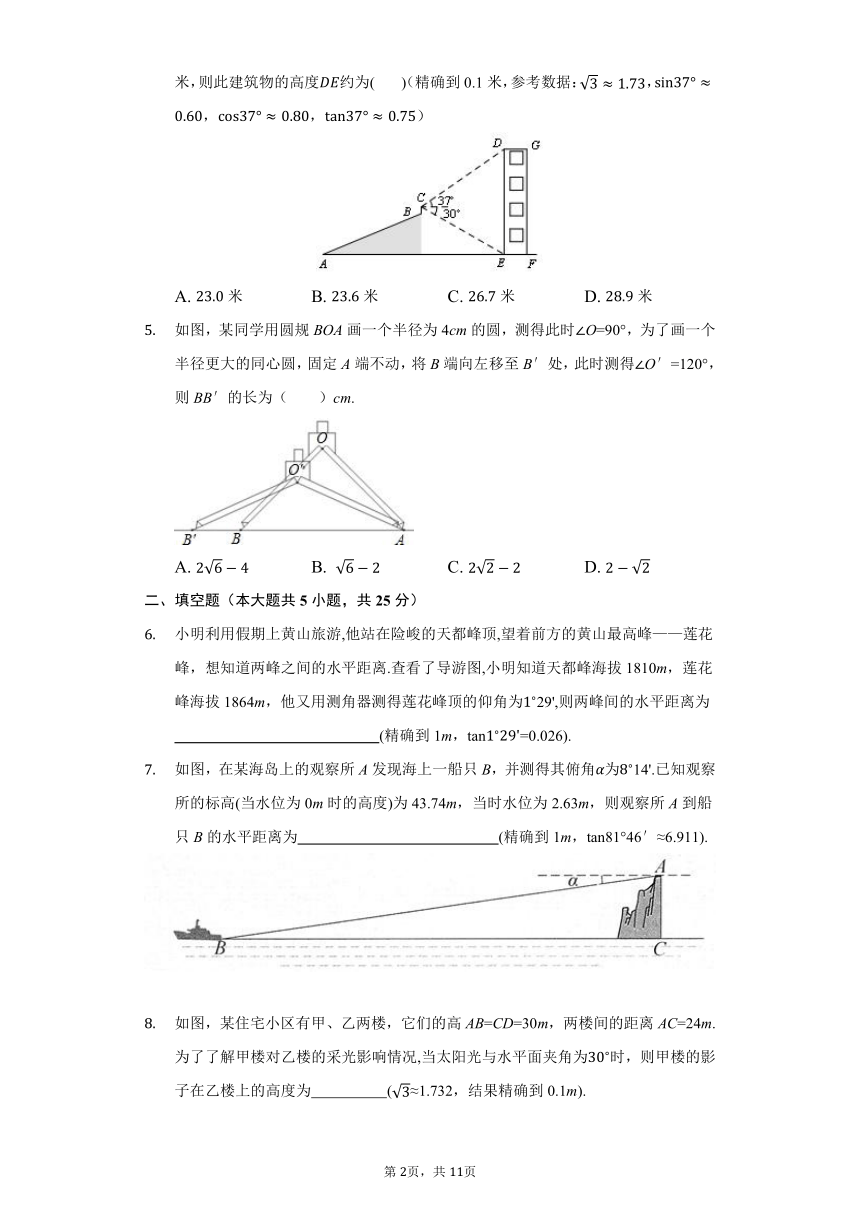
某同学利用数学知识测量建筑物的高度.他从点A出发沿着坡度为的斜坡AB步行26米到达点B处,用测角仪测得建筑物顶端D的仰角为,建筑物底端E的俯角为.若为水平的地面,侧角仪竖直放置,其高度米,则此建筑物的高度约为( )(精确到0.1米,参考数据:,,,)
A. 米 B. 米 C. 米 D. 米
如图,某同学用圆规BOA画一个半径为4cm的圆,测得此时∠O=90°,为了画一个半径更大的同心圆,固定A端不动,将B端向左移至B′处,此时测得∠O′=120°,则BB′的长为( )cm.
A. B. C. D.
二、填空题(本大题共5小题,共25分)
小明利用假期上黄山旅游,他站在险峻的天都峰顶,望着前方的黄山最高峰——莲花峰,想知道两峰之间的水平距离.查看了导游图,小明知道天都峰海拔1810m,莲花峰海拔1864m,他又用测角器测得莲花峰顶的仰角为29',则两峰间的水平距离为 (精确到1m,tan=0.026).
如图,在某海岛上的观察所A发现海上一船只B,并测得其俯角为14'.已知观察所的标高(当水位为0m时的高度)为43.74m,当时水位为2.63m,则观察所A到船只B的水平距离为 (精确到1m,tan81°46′≈6.911).
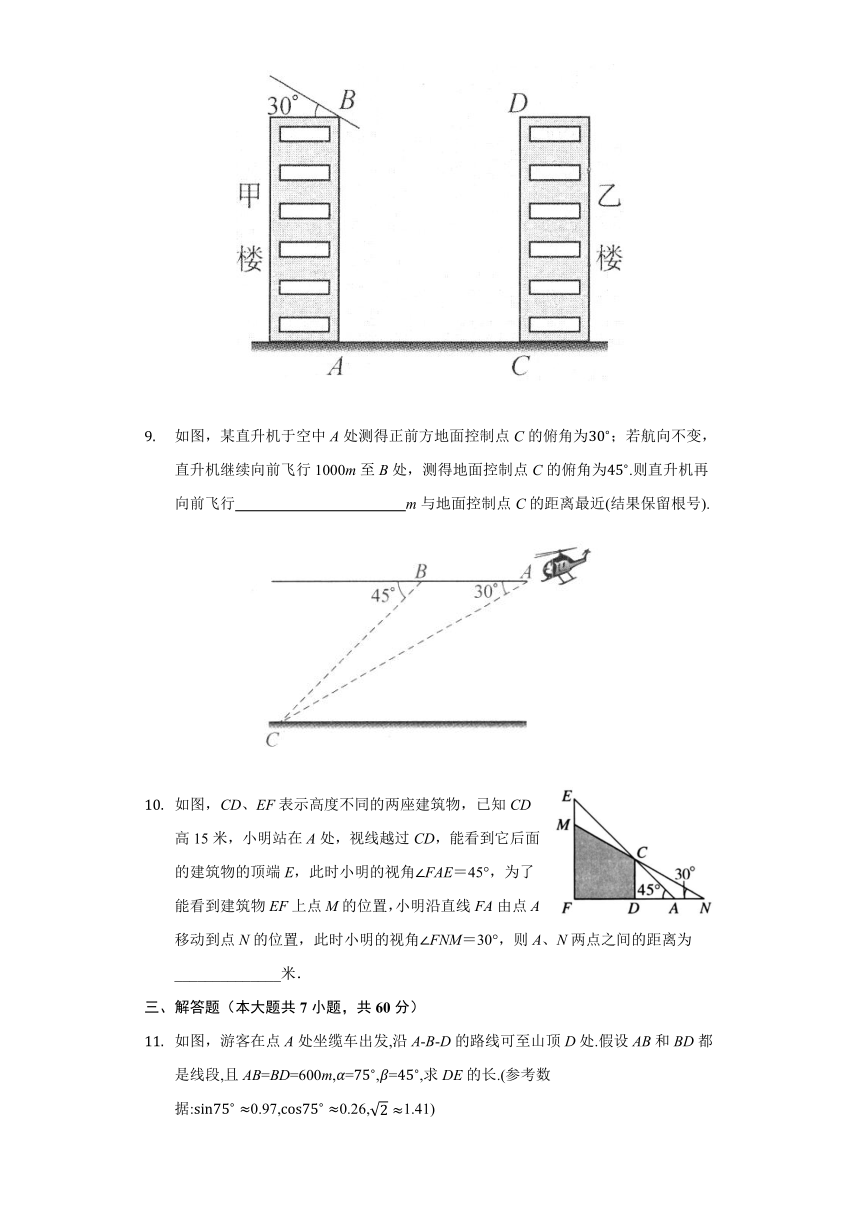
如图,某住宅小区有甲、乙两楼,它们的高AB=CD=30m,两楼间的距离AC=24m.为了了解甲楼对乙楼的采光影响情况,当太阳光与水平面夹角为时,则甲楼的影子在乙楼上的高度为 (≈1.732,结果精确到0.1m).
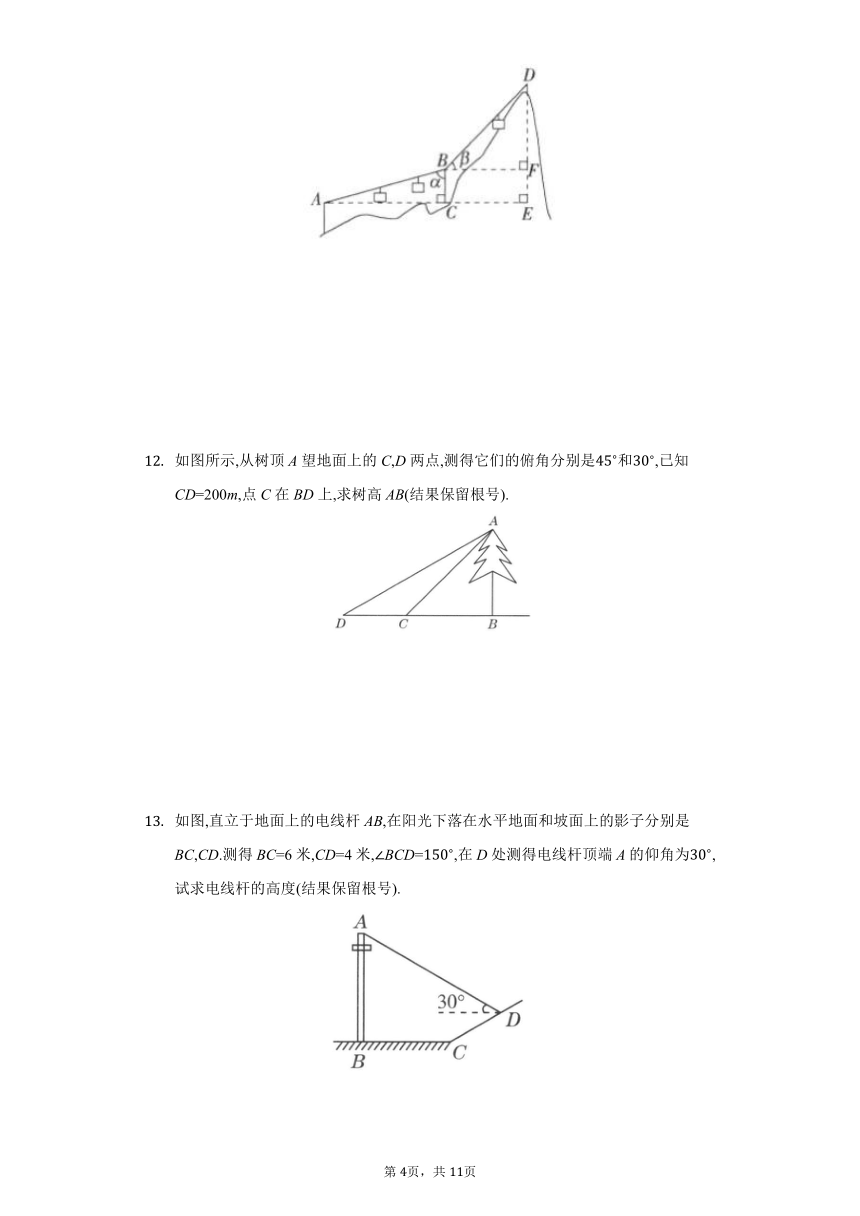
如图,某直升机于空中A处测得正前方地面控制点C的俯角为;若航向不变,直升机继续向前飞行1000m至B处,测得地面控制点C的俯角为.则直升机再向前飞行 m与地面控制点C的距离最近(结果保留根号).
如图,CD、EF表示高度不同的两座建筑物,已知CD高15米,小明站在A处,视线越过CD,能看到它后面的建筑物的顶端E,此时小明的视角∠FAE=45°,为了能看到建筑物EF上点M的位置,小明沿直线FA由点A移动到点N的位置,此时小明的视角∠FNM=30°,则A、N两点之间的距离为______________米.
三、解答题(本大题共7小题,共60分)
如图,游客在点A处坐缆车出发,沿A-B-D的路线可至山顶D处.假设AB和BD都是线段,且AB=BD=600m,=,=,求DE的长.(参考数据:0.97,0.26,1.41)
如图所示,从树顶A望地面上的C,D两点,测得它们的俯角分别是和,已知CD=200m,点C在BD上,求树高AB(结果保留根号).
如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC,CD.测得BC=6米,CD=4米,BCD=,在D处测得电线杆顶端A的仰角为,试求电线杆的高度(结果保留根号).
夏季多雨,在山坡CD处出现了滑坡,为了测量山体滑坡的坡面长度CD,探测队在距离坡底C点米处的E点用热气球进行数据监测,当热气球垂直升腾到B点时观察滑坡的终端C点,俯视角为60°,当热气球继续垂直升腾90米到达A点,此时探测到滑坡的始端D点,俯视角为45°,若滑坡的山体坡角∠DCH为30°,求山体滑坡的坡面长度CD的长.(计算保留根号)
如图所示,天空中有一个静止的广告气球C,从地面点A测得点C的仰角为,从地面点B测得点C的仰角为.已知AB=20m,点C和直线AB在同一平面内,求气球离地面的高度(结果保留根号).
时代购物广场要修建一个地下停车场,停车场的入口设计示意图如图所示,其中斜坡AD的倾斜角为,一楼到地下停车场的垂直高度CD=2.8m,一楼到地平线的距离BC=1m.
(1)为保证斜坡的倾斜角为,应在地平线上距点B多远的A处开始斜坡的施工 (结果精确到0.1米)
(2)如果给该购物广场送货的货车的高度为2.5m,那么按这样的设计能否保证货车顺利进入地下停车场 说明理由.(参考数据:0.31,0.95,0.32)
图1是一款折叠式跑步机,由支杆AE(点A、E固定),滑动杆PF和底座AD组成,AC为滑槽,图2是其侧面简化示意图,忽略跑步机的厚度,已知AE=60cm,AC=120cm,收纳时,当滑动端点P向右滑至点C时,滑动杆PF恰好与滑槽AC重合.
(1)如图3,当滑动端点P滑至AC的中点B时,求点F到底座AD的距离;
(2)当滑动端点P从点B向左滑动到点Q,PF与AD的夹角是70°时,小明观察点F处的仪表盘视角为最佳,求此时滑动端点P继续向左滑动的距离BQ的长(参考数据:,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,结果保留一位小数).
参考答案
1.【答案】B
2.【答案】D
3.【答案】A
4.【答案】C
5.【答案】A
6.【答案】2077m
7.【答案】284m
8.【答案】16.1m
9.【答案】
10.【答案】
11.【答案】解:在RtBDF中,由=可得,
DF=BD=600=600=300423(m).
在RtABC中,由=可得,
BC=AB=6006000.26=156(m).
所以DE=DF+EF=DF+BC=423+156=579(m).
故DE的长约为579m.
12.【答案】解:由题意可得BC==AB,BD==AB,
CD=BD-BC=(-1)AB.
CD=200m,
AB=100(+1)m.
答:树高为100(+1)m.
13.【答案】解:延长AD交BC的延长线于点E,过点D作DFCE于点F.
在RtDCF中,CD=4米,DCF=-=,
则DF=CDDCF=4=2(米),
CF=CDDCF=4=2(米).
在RtDEF中,E=,
E===,
解得EF=2米.
在RtABE中,BE=BC+CF+FE=6+2+2=(6+4)(米),
E===,解得AB=(4+2)米,
即电线杆的高度是(4+2)米.
14.【答案】山体滑坡的坡面长度CD的长为(570﹣810)米.
15.【答案】解:如图所示, 过点C作CD ⊥AB于点D.
设气球离地面的高度是xm.
在RtADC中,CAD=,所以AD=CD=xm.
在RtCDB中,CBD=,
所以CBD==,则BD=xm.
因为AB=AD-BD,所以20=x-x,
解得x=30+10.
答:气球离地面的高度是(30+10)m.
16.【答案】 (1)由题意易知BAD=,
在RtABD中,AB=5.6(m).
答:应在地面上距点B约5.6m远的A处开始斜坡的施工.
(2)能,理由如下:
如图,过点C作CEAD于点E,
BAD+BDA=,BDA+DCE=,
ECD=BAD=,
在RtCED中,CE=CD2.80.95=2.66(m),
2.66>2.5,
能保证货车顺利进入地下停车场.
17.【答案】解:(1)如图1,
连接AF,由题意可知AB=AE=BE=EF=60,
∴△ABF是直角三角形,且∠FAB=90°,
∴FA=≈103.8(cm),
(2)如图2,
过点E作EM⊥AB,垂足为M,
设BQ=x,则MQ=AQ=,
在Rt△EMQ中,cos∠MQE=,
∴cos70°=,
即,
解得:x≈19.2(cm),
∴此时滑动的距离约为19.2cm.
第2页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共5小题,共25分)
如图,一棵大树被台风拦腰刮断,树根A到刮断点P的长度是4米,折断部分PB与地面成40°的夹角,那么原来树的长度是( )米.
A. B. C. D.
秀秀和山山在水平的地面上放风筝,某一时刻两人的风筝正好都停在对方的正上方,即此时AC⊥AB,DB⊥AB,两人之间的距离AB为120米,若两人的风筝线与水平线的夹角分别为α和β,则两人放出的风筝线AD与BC的长度和为(忽略两人的身高与手臂长度)( )米
A. B.
C. D.
如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底点G为BC的中点,则矮建筑物的高CD为( )
A. 米 B. 米 C. 米 D. 米
某同学利用数学知识测量建筑物的高度.他从点A出发沿着坡度为的斜坡AB步行26米到达点B处,用测角仪测得建筑物顶端D的仰角为,建筑物底端E的俯角为.若为水平的地面,侧角仪竖直放置,其高度米,则此建筑物的高度约为( )(精确到0.1米,参考数据:,,,)
A. 米 B. 米 C. 米 D. 米
如图,某同学用圆规BOA画一个半径为4cm的圆,测得此时∠O=90°,为了画一个半径更大的同心圆,固定A端不动,将B端向左移至B′处,此时测得∠O′=120°,则BB′的长为( )cm.
A. B. C. D.
二、填空题(本大题共5小题,共25分)
小明利用假期上黄山旅游,他站在险峻的天都峰顶,望着前方的黄山最高峰——莲花峰,想知道两峰之间的水平距离.查看了导游图,小明知道天都峰海拔1810m,莲花峰海拔1864m,他又用测角器测得莲花峰顶的仰角为29',则两峰间的水平距离为 (精确到1m,tan=0.026).
如图,在某海岛上的观察所A发现海上一船只B,并测得其俯角为14'.已知观察所的标高(当水位为0m时的高度)为43.74m,当时水位为2.63m,则观察所A到船只B的水平距离为 (精确到1m,tan81°46′≈6.911).
如图,某住宅小区有甲、乙两楼,它们的高AB=CD=30m,两楼间的距离AC=24m.为了了解甲楼对乙楼的采光影响情况,当太阳光与水平面夹角为时,则甲楼的影子在乙楼上的高度为 (≈1.732,结果精确到0.1m).
如图,某直升机于空中A处测得正前方地面控制点C的俯角为;若航向不变,直升机继续向前飞行1000m至B处,测得地面控制点C的俯角为.则直升机再向前飞行 m与地面控制点C的距离最近(结果保留根号).
如图,CD、EF表示高度不同的两座建筑物,已知CD高15米,小明站在A处,视线越过CD,能看到它后面的建筑物的顶端E,此时小明的视角∠FAE=45°,为了能看到建筑物EF上点M的位置,小明沿直线FA由点A移动到点N的位置,此时小明的视角∠FNM=30°,则A、N两点之间的距离为______________米.
三、解答题(本大题共7小题,共60分)
如图,游客在点A处坐缆车出发,沿A-B-D的路线可至山顶D处.假设AB和BD都是线段,且AB=BD=600m,=,=,求DE的长.(参考数据:0.97,0.26,1.41)
如图所示,从树顶A望地面上的C,D两点,测得它们的俯角分别是和,已知CD=200m,点C在BD上,求树高AB(结果保留根号).
如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC,CD.测得BC=6米,CD=4米,BCD=,在D处测得电线杆顶端A的仰角为,试求电线杆的高度(结果保留根号).
夏季多雨,在山坡CD处出现了滑坡,为了测量山体滑坡的坡面长度CD,探测队在距离坡底C点米处的E点用热气球进行数据监测,当热气球垂直升腾到B点时观察滑坡的终端C点,俯视角为60°,当热气球继续垂直升腾90米到达A点,此时探测到滑坡的始端D点,俯视角为45°,若滑坡的山体坡角∠DCH为30°,求山体滑坡的坡面长度CD的长.(计算保留根号)
如图所示,天空中有一个静止的广告气球C,从地面点A测得点C的仰角为,从地面点B测得点C的仰角为.已知AB=20m,点C和直线AB在同一平面内,求气球离地面的高度(结果保留根号).
时代购物广场要修建一个地下停车场,停车场的入口设计示意图如图所示,其中斜坡AD的倾斜角为,一楼到地下停车场的垂直高度CD=2.8m,一楼到地平线的距离BC=1m.
(1)为保证斜坡的倾斜角为,应在地平线上距点B多远的A处开始斜坡的施工 (结果精确到0.1米)
(2)如果给该购物广场送货的货车的高度为2.5m,那么按这样的设计能否保证货车顺利进入地下停车场 说明理由.(参考数据:0.31,0.95,0.32)
图1是一款折叠式跑步机,由支杆AE(点A、E固定),滑动杆PF和底座AD组成,AC为滑槽,图2是其侧面简化示意图,忽略跑步机的厚度,已知AE=60cm,AC=120cm,收纳时,当滑动端点P向右滑至点C时,滑动杆PF恰好与滑槽AC重合.
(1)如图3,当滑动端点P滑至AC的中点B时,求点F到底座AD的距离;
(2)当滑动端点P从点B向左滑动到点Q,PF与AD的夹角是70°时,小明观察点F处的仪表盘视角为最佳,求此时滑动端点P继续向左滑动的距离BQ的长(参考数据:,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,结果保留一位小数).
参考答案
1.【答案】B
2.【答案】D
3.【答案】A
4.【答案】C
5.【答案】A
6.【答案】2077m
7.【答案】284m
8.【答案】16.1m
9.【答案】
10.【答案】
11.【答案】解:在RtBDF中,由=可得,
DF=BD=600=600=300423(m).
在RtABC中,由=可得,
BC=AB=6006000.26=156(m).
所以DE=DF+EF=DF+BC=423+156=579(m).
故DE的长约为579m.
12.【答案】解:由题意可得BC==AB,BD==AB,
CD=BD-BC=(-1)AB.
CD=200m,
AB=100(+1)m.
答:树高为100(+1)m.
13.【答案】解:延长AD交BC的延长线于点E,过点D作DFCE于点F.
在RtDCF中,CD=4米,DCF=-=,
则DF=CDDCF=4=2(米),
CF=CDDCF=4=2(米).
在RtDEF中,E=,
E===,
解得EF=2米.
在RtABE中,BE=BC+CF+FE=6+2+2=(6+4)(米),
E===,解得AB=(4+2)米,
即电线杆的高度是(4+2)米.
14.【答案】山体滑坡的坡面长度CD的长为(570﹣810)米.
15.【答案】解:如图所示, 过点C作CD ⊥AB于点D.
设气球离地面的高度是xm.
在RtADC中,CAD=,所以AD=CD=xm.
在RtCDB中,CBD=,
所以CBD==,则BD=xm.
因为AB=AD-BD,所以20=x-x,
解得x=30+10.
答:气球离地面的高度是(30+10)m.
16.【答案】 (1)由题意易知BAD=,
在RtABD中,AB=5.6(m).
答:应在地面上距点B约5.6m远的A处开始斜坡的施工.
(2)能,理由如下:
如图,过点C作CEAD于点E,
BAD+BDA=,BDA+DCE=,
ECD=BAD=,
在RtCED中,CE=CD2.80.95=2.66(m),
2.66>2.5,
能保证货车顺利进入地下停车场.
17.【答案】解:(1)如图1,
连接AF,由题意可知AB=AE=BE=EF=60,
∴△ABF是直角三角形,且∠FAB=90°,
∴FA=≈103.8(cm),
(2)如图2,
过点E作EM⊥AB,垂足为M,
设BQ=x,则MQ=AQ=,
在Rt△EMQ中,cos∠MQE=,
∴cos70°=,
即,
解得:x≈19.2(cm),
∴此时滑动的距离约为19.2cm.
第2页,共2页
