2021-2022学年沪科版九年级数学上册23.2.4 利用解直角三角形解方位角的问题同步测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年沪科版九年级数学上册23.2.4 利用解直角三角形解方位角的问题同步测试卷(Word版含答案) | 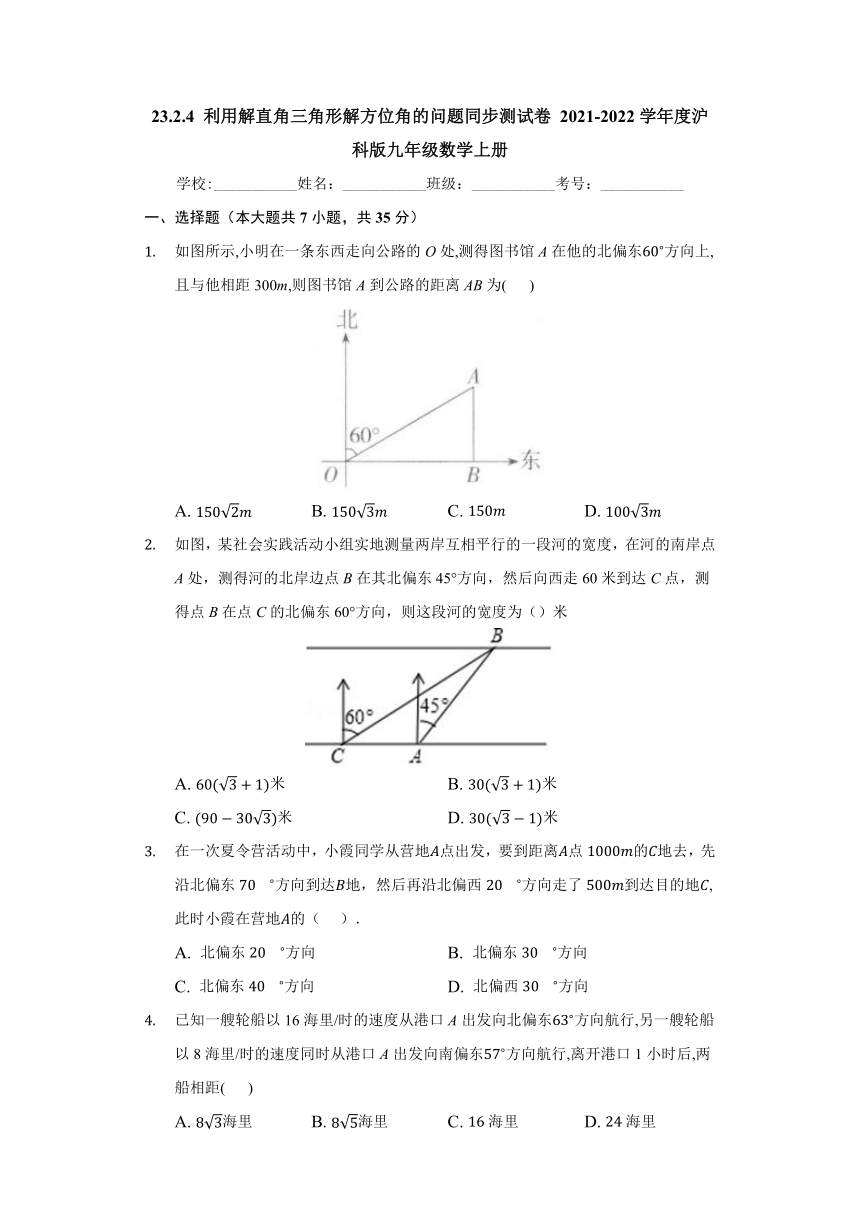 | |
| 格式 | docx | ||
| 文件大小 | 117.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 13:30:29 | ||
图片预览


文档简介
23.2.4 利用解直角三角形解方位角的问题同步测试卷 2021-2022学年度沪科版九年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共7小题,共35分)
如图所示,小明在一条东西走向公路的O处,测得图书馆A在他的北偏东方向上,且与他相距300m,则图书馆A到公路的距离AB为( )
A. B. C. D.
如图,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60米到达C点,测得点B在点C的北偏东60°方向,则这段河的宽度为()米
A. 米 B. 米
C. 米 D. 米
在一次夏令营活动中,小霞同学从营地点出发,要到距离点的地去,先沿北偏东方向到达地,然后再沿北偏西方向走了到达目的地,此时小霞在营地的( ).
A. 北偏东方向 B. 北偏东方向
C. 北偏东方向 D. 北偏西方向
已知一艘轮船以16海里/时的速度从港口A出发向北偏东方向航行,另一艘轮船以8海里/时的速度同时从港口A出发向南偏东方向航行,离开港口1小时后,两船相距( )
A. 海里 B. 海里 C. 海里 D. 海里
一艘在南北航线上的测量船,于点A处测得海岛B在点A的南偏东方向,继续向南航行30nmile到达点C时,测得海岛B在点C的北偏东方向,那么海岛B离此航线的最近距离是(精确到0.01nmile)( )
A. B. C. D.
在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30 m,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10 m.则河的宽度为( ) m
A. B. C. D.
如图,建筑工地划出了三角形安全区(△ABC),一人从A点出发,沿北偏东53°方向走50m到达C点,另一人从B点出发,沿北偏西53°方向走100m到达C点,则点A与点B相距()( tan53°=)
A. B. C. D.
二、填空题(本大题共2小题,共10分)
一船向东航行,上午9:00到达灯塔C的西南60n mile的A处,上午10:00到达灯塔C的正南的B处.则这艘船的航行速度为 n mile/h(结果保留根号).
如图,一船沿北偏东的方向离开A港直线航行,航行50n mile后到达C处,改变方向向东航行,又走了40n mile到达B处,则= (精确到);
三、解答题(本大题共4小题,共55分)
周六下午,王武和父亲开车出去办事,如图,在A处测得其北偏东处有一座移动信号发射塔C,当车以每小时60千米的速度向正东方向行驶20分钟到达B处时,测得信号发射塔C在其北偏西处,请你求出此时车和发射塔之间的距离BC.(结果保留根号)
如图所示,小明同学在东西走向的文一路A处测得一处公共自行车租用服务点P在北偏东方向上,从A处向东走90米到达B处,又测得该服务点P在北偏东方向上,求该服务点P到文一路的距离PC(结果保留根号).
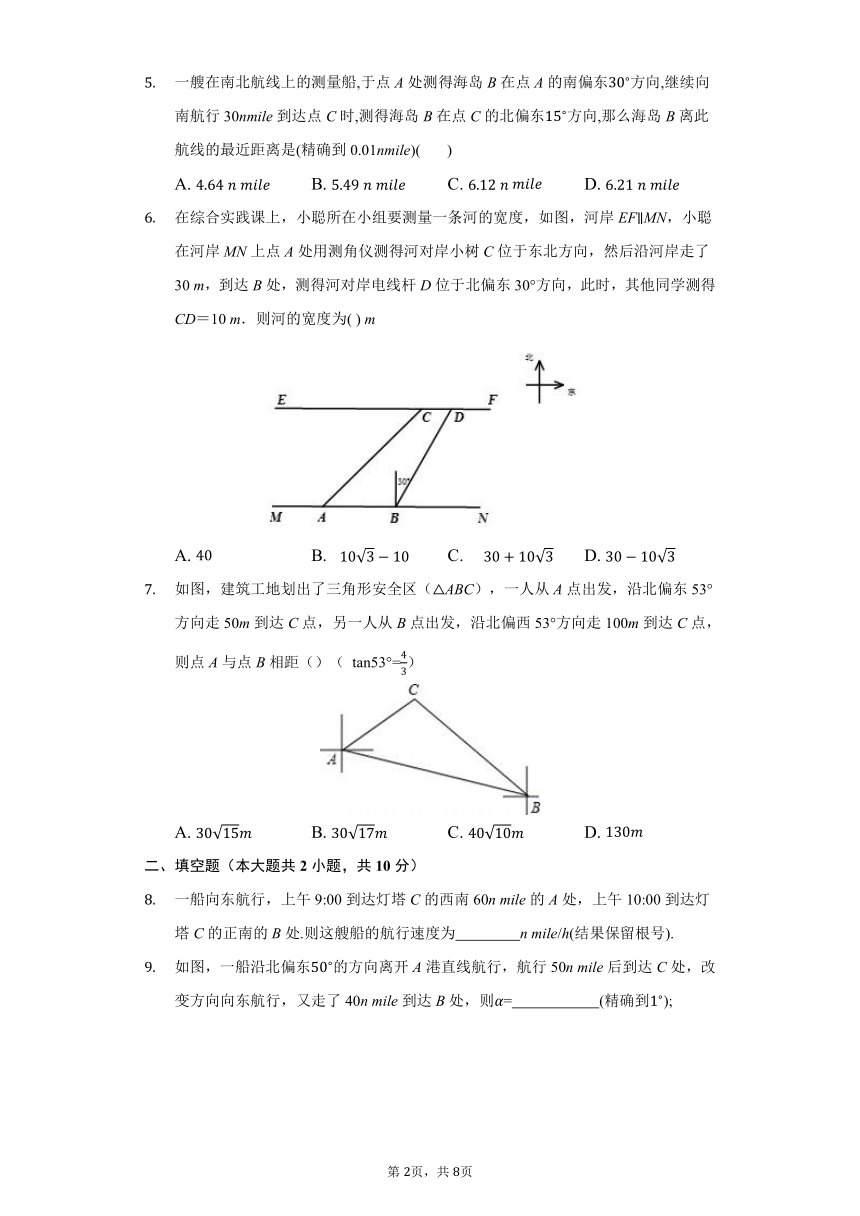
如图所示,一艘轮船自西向东航行,在A处测得北偏东68.的方向上有一座小岛C,继续向东航行60海里到达B处,测得小岛C此时在轮船的北偏东26.的方向上,之后,轮船继续向东航行多少海里,距离小岛C最近 (结果精确到1海里.参考数据:21.,21.,63.,63.2)
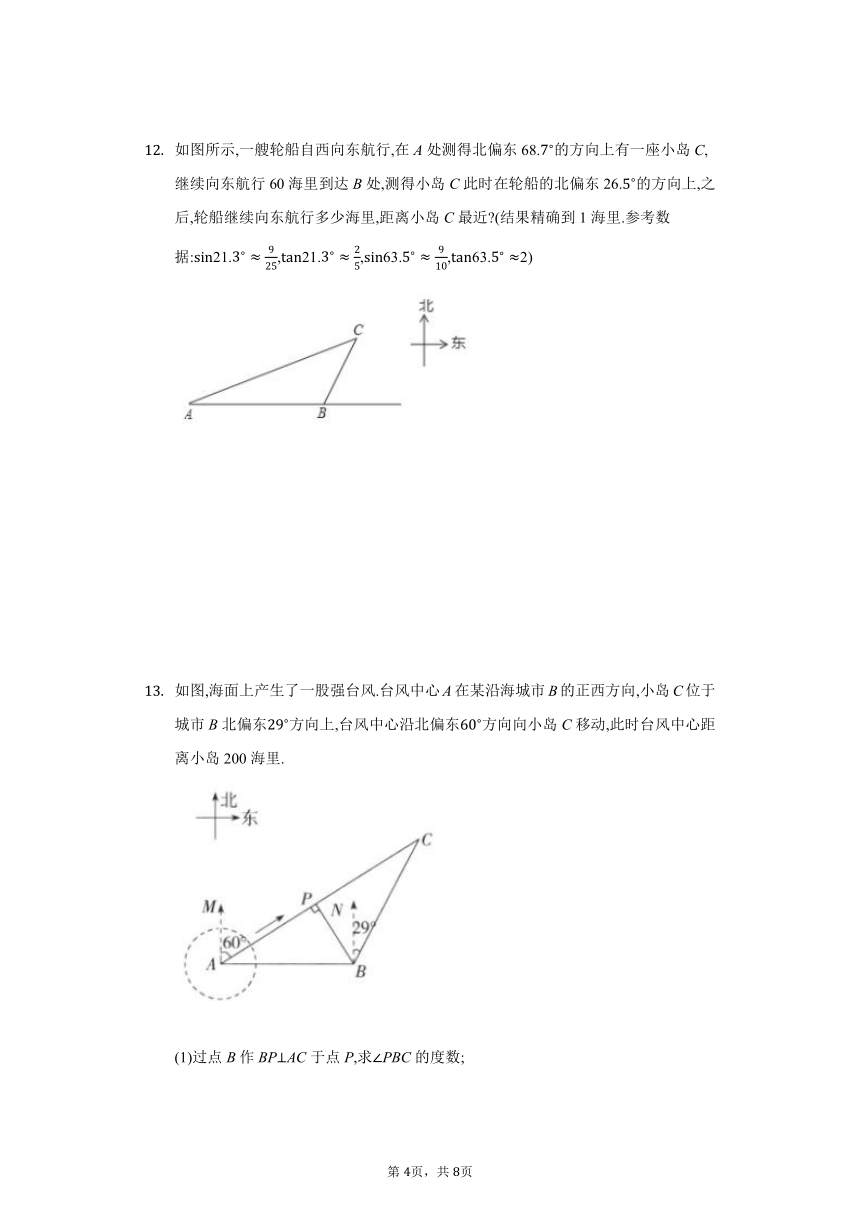
如图,海面上产生了一股强台风.台风中心A在某沿海城市B的正西方向,小岛C位于城市B北偏东方向上,台风中心沿北偏东方向向小岛C移动,此时台风中心距离小岛200海里.
(1)过点B作BPAC于点P,求PBC的度数;
(2)据监测,在距离台风中心50海里范围内均会受到台风影响(假设台风在移动过程中风力保持不变).问:在台风移动过程中,沿海城市B是否会受到台风影响 请说明理由.(参考数据:0.52,0.86,0.60,1.73)
参考答案
1.【答案】C
2.【答案】B
3.【答案】C
4.【答案】A
5.【答案】B
6.【答案】C
7.【答案】B
8.【答案】
9.【答案】68°
10.【答案】解:过B 作BDAC于D, 如图所示:
则BDA=BDC=,
由题意得AB=60=20(千米),
BAC=-=,
ABC=-=,
ABD=,C=-BAC-ABC=,
AD=AB=10(千米),BD=AD=10(千米),
BC=BD=10(千米).
答:此时车和发射塔之间的距离BC为10千米.
11.【答案】解:在RtPBC中,=PBC,
BC==PC.
在RtPAC中,=PAC,
AC==PC.
AB=AC-BC=90米,
PC-PC=90.
解得PC=45米.
答:该服务点P到文一路的距离PC为45米.
12.【答案】解:如图所示,过点C作AB的垂线,交直线AB于点D,
得到RtACD与RtBCD.设BD=x海里.
由题意,得CBD=-26.=63.,CAD=-68.=21..
在RtBCD中,CBD=,
CD=x63.海里.
在RtACD中,AD=AB+BD=(60+x)海里,A=,
CD=(60+x)21.海里,
x63.=(60+x)21.,
即2x=(60+x),解得x=15.
答:轮船继续向东航行约15海里,距离小岛C最近.
13.【答案】解:(1)MAC=,MAB=,
BAC=,
又BPAC,
APB=,
ABP=,
又CBN=,ABN=,
ABC=,
PBC=ABC-ABP=.
(2)不会受到影响.理由如下:
由(1)可知,PBC=,
C=-PBC=,
又0.60,
0.60=,
设 BP=x 海里,则 AP=x 海里,CP=x 海里,
x+x=200,
解得 x59,
59>50,
沿海城市 B 不会受到台风影响.
第2页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共7小题,共35分)
如图所示,小明在一条东西走向公路的O处,测得图书馆A在他的北偏东方向上,且与他相距300m,则图书馆A到公路的距离AB为( )
A. B. C. D.
如图,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60米到达C点,测得点B在点C的北偏东60°方向,则这段河的宽度为()米
A. 米 B. 米
C. 米 D. 米
在一次夏令营活动中,小霞同学从营地点出发,要到距离点的地去,先沿北偏东方向到达地,然后再沿北偏西方向走了到达目的地,此时小霞在营地的( ).
A. 北偏东方向 B. 北偏东方向
C. 北偏东方向 D. 北偏西方向
已知一艘轮船以16海里/时的速度从港口A出发向北偏东方向航行,另一艘轮船以8海里/时的速度同时从港口A出发向南偏东方向航行,离开港口1小时后,两船相距( )
A. 海里 B. 海里 C. 海里 D. 海里
一艘在南北航线上的测量船,于点A处测得海岛B在点A的南偏东方向,继续向南航行30nmile到达点C时,测得海岛B在点C的北偏东方向,那么海岛B离此航线的最近距离是(精确到0.01nmile)( )
A. B. C. D.
在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30 m,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10 m.则河的宽度为( ) m
A. B. C. D.
如图,建筑工地划出了三角形安全区(△ABC),一人从A点出发,沿北偏东53°方向走50m到达C点,另一人从B点出发,沿北偏西53°方向走100m到达C点,则点A与点B相距()( tan53°=)
A. B. C. D.
二、填空题(本大题共2小题,共10分)
一船向东航行,上午9:00到达灯塔C的西南60n mile的A处,上午10:00到达灯塔C的正南的B处.则这艘船的航行速度为 n mile/h(结果保留根号).
如图,一船沿北偏东的方向离开A港直线航行,航行50n mile后到达C处,改变方向向东航行,又走了40n mile到达B处,则= (精确到);
三、解答题(本大题共4小题,共55分)
周六下午,王武和父亲开车出去办事,如图,在A处测得其北偏东处有一座移动信号发射塔C,当车以每小时60千米的速度向正东方向行驶20分钟到达B处时,测得信号发射塔C在其北偏西处,请你求出此时车和发射塔之间的距离BC.(结果保留根号)
如图所示,小明同学在东西走向的文一路A处测得一处公共自行车租用服务点P在北偏东方向上,从A处向东走90米到达B处,又测得该服务点P在北偏东方向上,求该服务点P到文一路的距离PC(结果保留根号).
如图所示,一艘轮船自西向东航行,在A处测得北偏东68.的方向上有一座小岛C,继续向东航行60海里到达B处,测得小岛C此时在轮船的北偏东26.的方向上,之后,轮船继续向东航行多少海里,距离小岛C最近 (结果精确到1海里.参考数据:21.,21.,63.,63.2)
如图,海面上产生了一股强台风.台风中心A在某沿海城市B的正西方向,小岛C位于城市B北偏东方向上,台风中心沿北偏东方向向小岛C移动,此时台风中心距离小岛200海里.
(1)过点B作BPAC于点P,求PBC的度数;
(2)据监测,在距离台风中心50海里范围内均会受到台风影响(假设台风在移动过程中风力保持不变).问:在台风移动过程中,沿海城市B是否会受到台风影响 请说明理由.(参考数据:0.52,0.86,0.60,1.73)
参考答案
1.【答案】C
2.【答案】B
3.【答案】C
4.【答案】A
5.【答案】B
6.【答案】C
7.【答案】B
8.【答案】
9.【答案】68°
10.【答案】解:过B 作BDAC于D, 如图所示:
则BDA=BDC=,
由题意得AB=60=20(千米),
BAC=-=,
ABC=-=,
ABD=,C=-BAC-ABC=,
AD=AB=10(千米),BD=AD=10(千米),
BC=BD=10(千米).
答:此时车和发射塔之间的距离BC为10千米.
11.【答案】解:在RtPBC中,=PBC,
BC==PC.
在RtPAC中,=PAC,
AC==PC.
AB=AC-BC=90米,
PC-PC=90.
解得PC=45米.
答:该服务点P到文一路的距离PC为45米.
12.【答案】解:如图所示,过点C作AB的垂线,交直线AB于点D,
得到RtACD与RtBCD.设BD=x海里.
由题意,得CBD=-26.=63.,CAD=-68.=21..
在RtBCD中,CBD=,
CD=x63.海里.
在RtACD中,AD=AB+BD=(60+x)海里,A=,
CD=(60+x)21.海里,
x63.=(60+x)21.,
即2x=(60+x),解得x=15.
答:轮船继续向东航行约15海里,距离小岛C最近.
13.【答案】解:(1)MAC=,MAB=,
BAC=,
又BPAC,
APB=,
ABP=,
又CBN=,ABN=,
ABC=,
PBC=ABC-ABP=.
(2)不会受到影响.理由如下:
由(1)可知,PBC=,
C=-PBC=,
又0.60,
0.60=,
设 BP=x 海里,则 AP=x 海里,CP=x 海里,
x+x=200,
解得 x59,
59>50,
沿海城市 B 不会受到台风影响.
第2页,共2页
