2021-2022学年 沪科版九年级数学上册23.2.2 平面直角坐标系中的直线与坐标轴的夹角问题同步测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年 沪科版九年级数学上册23.2.2 平面直角坐标系中的直线与坐标轴的夹角问题同步测试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 84.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 13:29:08 | ||
图片预览


文档简介
23.2.2 平面直角坐标系中的直线与坐标轴的夹角问题同步测试卷 2021-2022学年度沪科版九年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共4小题,共20分)
在平面直角坐标系中,点P的坐标为(2,3),OP与x轴正半轴的夹角的正弦值为( )
A. B. C. D.
如图,点P在反比例函数y=的图象上,且横坐标为1,过点P作两条坐标轴的平行线,分别与x轴、y轴交于A、B两点,则直线AB与x轴所夹锐角的正切值为( )
A. B.
C. D.
如图,以O为圆心,半径为1的弧交坐标轴于A,B两点,P是AB弧上一点(不与A,B重合),连接设∠POB=α,则点P的坐标是( )
A. B.
C. D.
如图,二次函数y=-x2+x+3的图象与x轴交于点A、B,与y轴交于点C,点D在该抛物线上,且点D的横坐标为2,连接BC、BD,设∠OCB=α,∠DBC=β,则cos(α-β)的值是( )
A. B. C. D.
二、填空题(本大题共5小题,共20分)
直线y=kx-3与y轴相交所成的锐角的正切值为,则k的值为 .
求直线y=x-5的向上方向与x轴正方向所夹的锐角为
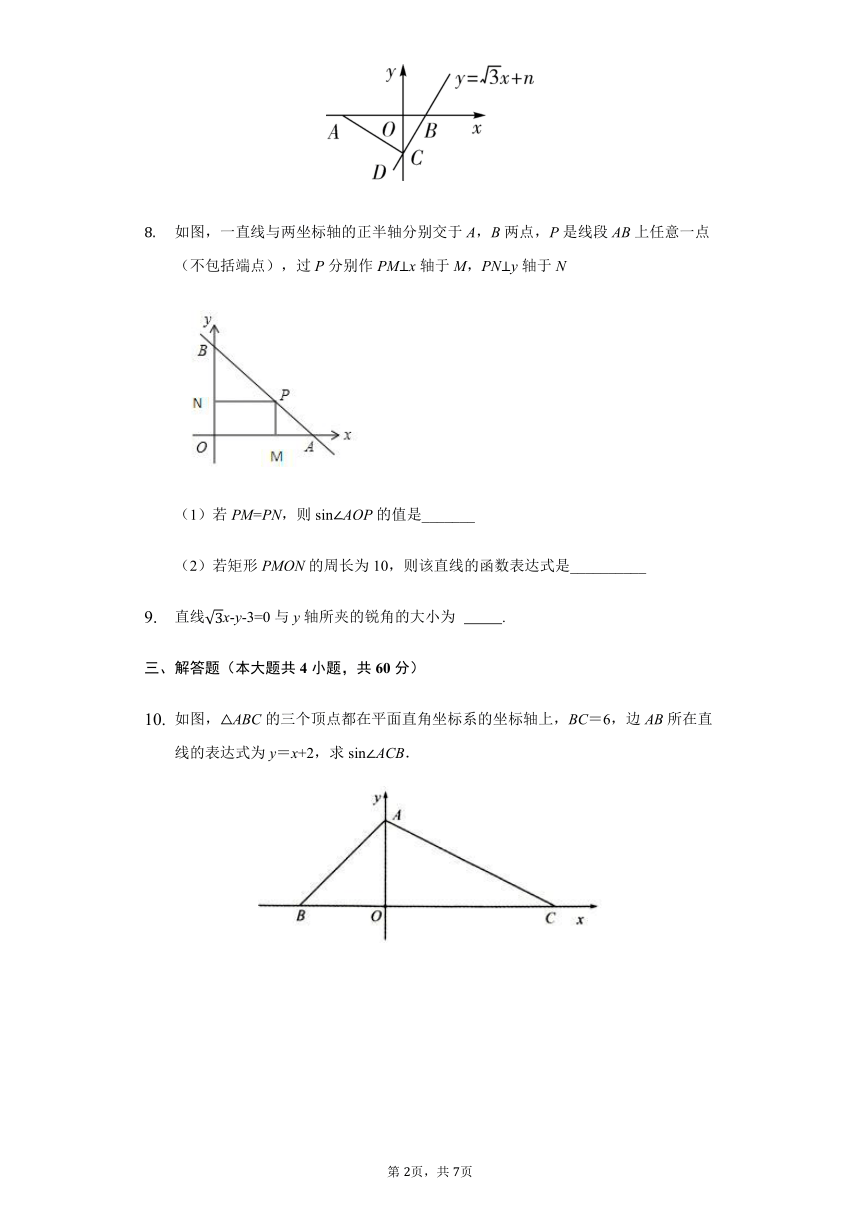
如图,点A的坐标为(-4,0),直线y=x+n与坐标轴交于点B,C,连接AC,如果∠ACD=90°,则n的值为________.
如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过P分别作PM⊥x轴于M,PN⊥y轴于N
(1)若PM=PN,则sinAOP的值是_______
(2)若矩形PMON的周长为10,则该直线的函数表达式是__________
直线x-y-3=0与y轴所夹的锐角的大小为 .
三、解答题(本大题共4小题,共60分)
如图,△ABC的三个顶点都在平面直角坐标系的坐标轴上,BC=6,边AB所在直线的表达式为y=x+2,求sin∠ACB.
如图所示,在平面直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,BOA=.求:
(1)点B的坐标;
(2)BAO的值.
一次函数y=(k-)x-3k+10(k为偶数)的图象经过第一、二、三象限,与x轴、y轴分别交于A、B两点,过点B作一直线与坐标轴围成的三角形面积为2,交x轴于点C.
(1)求k的值;
(2)若一抛物线经过点A、B、C三点,求此抛物线的解析式.
(3)当抛物线开口向上时过A、B、C三点作△ABC,求tan∠ABC的值.
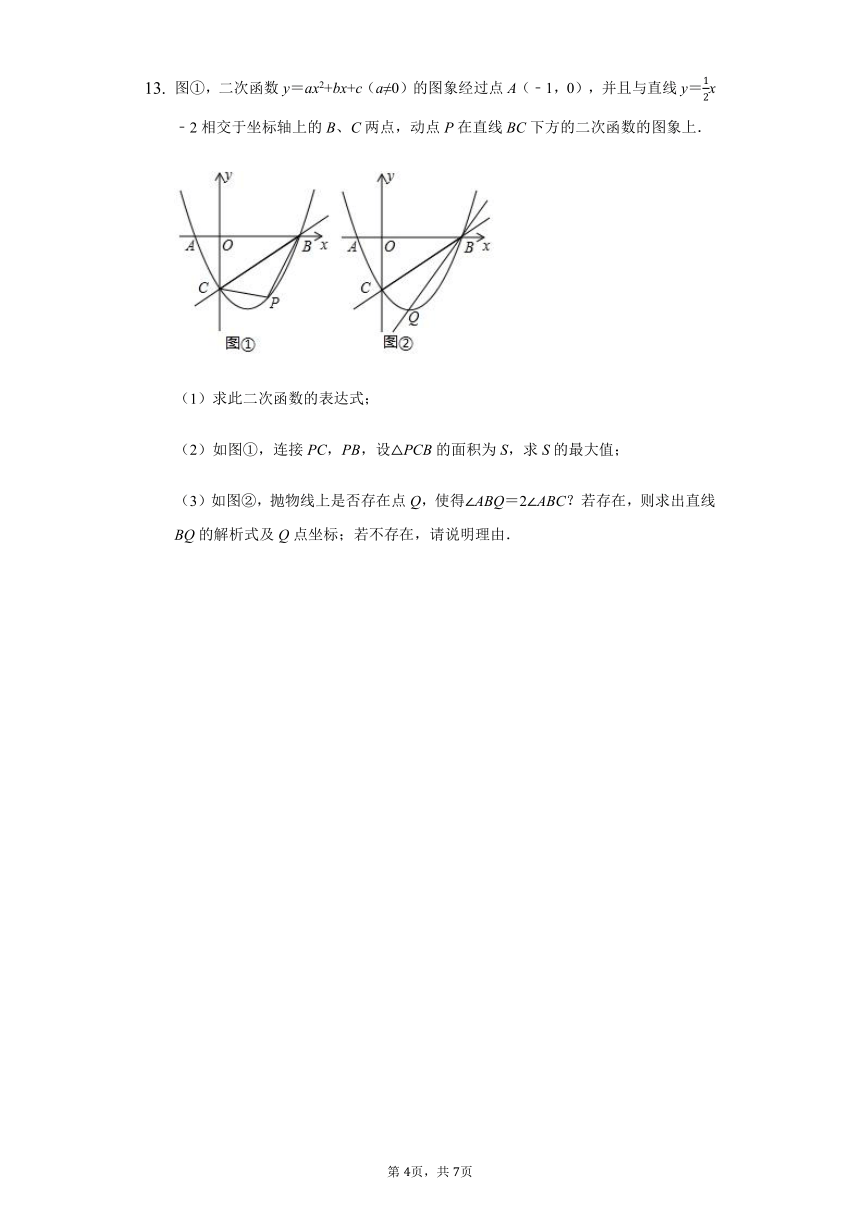
图①,二次函数y=ax2+bx+c(a≠0)的图象经过点A(﹣1,0),并且与直线y=x﹣2相交于坐标轴上的B、C两点,动点P在直线BC下方的二次函数的图象上.
(1)求此二次函数的表达式;
(2)如图①,连接PC,PB,设△PCB的面积为S,求S的最大值;
(3)如图②,抛物线上是否存在点Q,使得∠ABQ=2∠ABC?若存在,则求出直线BQ的解析式及Q点坐标;若不存在,请说明理由.
参考答案
1.【答案】D
2.【答案】A
3.【答案】C
4.【答案】D
5.【答案】 3
6.【答案】60°
7.【答案】
8.【答案】(1)(2)y=-x+5
9.【答案】
10.【答案】解:∵直线AB的表达式为y=x+2,
∴当y=0时,x=-2,当x=0时,y=2,
∴点A(0,2),点B(-2,0),
∴OA=2,OB=2,
∵BC=6,
∴OC=BC-OB=6-2=4,
∴AC=,
∴
11.【答案】解:(1)如图所示,作BHOA,垂足为H.
在RtOHB中,BO=5,BOA=,
BH=3,
OH==4,
点B的坐标为(4,3).
(2)OA=10,OH=4,
AH=6.
在RtAHB中,AB==3,
BAO==.
12.【答案】解:(1)由题意得:,
解得<k<,
又k为偶数,
∴k=2;
(2)∵k=2,
∴一次函数为y=x+4,
∵图象与x轴、y轴分别交于A、B两点,
∴A(-3,0)、B(0,4),
∴OB=4,
∵S△BOC= OB OC=2,
∴=2,
∴OC=1,
∴C(1,0)或(-1,0),
若取C(1,0)、A(-3,0)、B(0,4),设y=a(x+3)(x-1),
将B(0,4)代入得4=-3a,
∴a=-.
∴抛物线为y=-x2-x+4,
若取C(-1,0)、A(-3,0)、B(0,4),设y=a(x+3)(x+1),
将B(0,4)代入得4=3a,
∴a=,
∴抛物线为y=x2+x+4;
(3)∵A(-3,0),B(0,4),
∴OA=3,OB=4,
∴AB==5,
如图,过C作CD⊥AB于D,则tan∠ABC=,
∵sin∠BAO==,cos∠BAO==,
∴=,=,
∴DC=,AD=,
∴BD=,
∴tan∠ABC=.
13.【答案】(1)y=x2﹣x﹣2;(2)﹣1<0,故S有最大值,当x=2时,S的最大值为4;(3)Q的坐标为(,﹣)或(﹣,).
第2页,共3页
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共4小题,共20分)
在平面直角坐标系中,点P的坐标为(2,3),OP与x轴正半轴的夹角的正弦值为( )
A. B. C. D.
如图,点P在反比例函数y=的图象上,且横坐标为1,过点P作两条坐标轴的平行线,分别与x轴、y轴交于A、B两点,则直线AB与x轴所夹锐角的正切值为( )
A. B.
C. D.
如图,以O为圆心,半径为1的弧交坐标轴于A,B两点,P是AB弧上一点(不与A,B重合),连接设∠POB=α,则点P的坐标是( )
A. B.
C. D.
如图,二次函数y=-x2+x+3的图象与x轴交于点A、B,与y轴交于点C,点D在该抛物线上,且点D的横坐标为2,连接BC、BD,设∠OCB=α,∠DBC=β,则cos(α-β)的值是( )
A. B. C. D.
二、填空题(本大题共5小题,共20分)
直线y=kx-3与y轴相交所成的锐角的正切值为,则k的值为 .
求直线y=x-5的向上方向与x轴正方向所夹的锐角为
如图,点A的坐标为(-4,0),直线y=x+n与坐标轴交于点B,C,连接AC,如果∠ACD=90°,则n的值为________.
如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过P分别作PM⊥x轴于M,PN⊥y轴于N
(1)若PM=PN,则sinAOP的值是_______
(2)若矩形PMON的周长为10,则该直线的函数表达式是__________
直线x-y-3=0与y轴所夹的锐角的大小为 .
三、解答题(本大题共4小题,共60分)
如图,△ABC的三个顶点都在平面直角坐标系的坐标轴上,BC=6,边AB所在直线的表达式为y=x+2,求sin∠ACB.
如图所示,在平面直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,BOA=.求:
(1)点B的坐标;
(2)BAO的值.
一次函数y=(k-)x-3k+10(k为偶数)的图象经过第一、二、三象限,与x轴、y轴分别交于A、B两点,过点B作一直线与坐标轴围成的三角形面积为2,交x轴于点C.
(1)求k的值;
(2)若一抛物线经过点A、B、C三点,求此抛物线的解析式.
(3)当抛物线开口向上时过A、B、C三点作△ABC,求tan∠ABC的值.
图①,二次函数y=ax2+bx+c(a≠0)的图象经过点A(﹣1,0),并且与直线y=x﹣2相交于坐标轴上的B、C两点,动点P在直线BC下方的二次函数的图象上.
(1)求此二次函数的表达式;
(2)如图①,连接PC,PB,设△PCB的面积为S,求S的最大值;
(3)如图②,抛物线上是否存在点Q,使得∠ABQ=2∠ABC?若存在,则求出直线BQ的解析式及Q点坐标;若不存在,请说明理由.
参考答案
1.【答案】D
2.【答案】A
3.【答案】C
4.【答案】D
5.【答案】 3
6.【答案】60°
7.【答案】
8.【答案】(1)(2)y=-x+5
9.【答案】
10.【答案】解:∵直线AB的表达式为y=x+2,
∴当y=0时,x=-2,当x=0时,y=2,
∴点A(0,2),点B(-2,0),
∴OA=2,OB=2,
∵BC=6,
∴OC=BC-OB=6-2=4,
∴AC=,
∴
11.【答案】解:(1)如图所示,作BHOA,垂足为H.
在RtOHB中,BO=5,BOA=,
BH=3,
OH==4,
点B的坐标为(4,3).
(2)OA=10,OH=4,
AH=6.
在RtAHB中,AB==3,
BAO==.
12.【答案】解:(1)由题意得:,
解得<k<,
又k为偶数,
∴k=2;
(2)∵k=2,
∴一次函数为y=x+4,
∵图象与x轴、y轴分别交于A、B两点,
∴A(-3,0)、B(0,4),
∴OB=4,
∵S△BOC= OB OC=2,
∴=2,
∴OC=1,
∴C(1,0)或(-1,0),
若取C(1,0)、A(-3,0)、B(0,4),设y=a(x+3)(x-1),
将B(0,4)代入得4=-3a,
∴a=-.
∴抛物线为y=-x2-x+4,
若取C(-1,0)、A(-3,0)、B(0,4),设y=a(x+3)(x+1),
将B(0,4)代入得4=3a,
∴a=,
∴抛物线为y=x2+x+4;
(3)∵A(-3,0),B(0,4),
∴OA=3,OB=4,
∴AB==5,
如图,过C作CD⊥AB于D,则tan∠ABC=,
∵sin∠BAO==,cos∠BAO==,
∴=,=,
∴DC=,AD=,
∴BD=,
∴tan∠ABC=.
13.【答案】(1)y=x2﹣x﹣2;(2)﹣1<0,故S有最大值,当x=2时,S的最大值为4;(3)Q的坐标为(,﹣)或(﹣,).
第2页,共3页
第1页,共1页
