2021-2022人教版(2019)高中数学选择性必修第二册5.2.2 导数的四则运算法则 课件(20张PPT)
文档属性
| 名称 | 2021-2022人教版(2019)高中数学选择性必修第二册5.2.2 导数的四则运算法则 课件(20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 00:00:00 | ||
图片预览







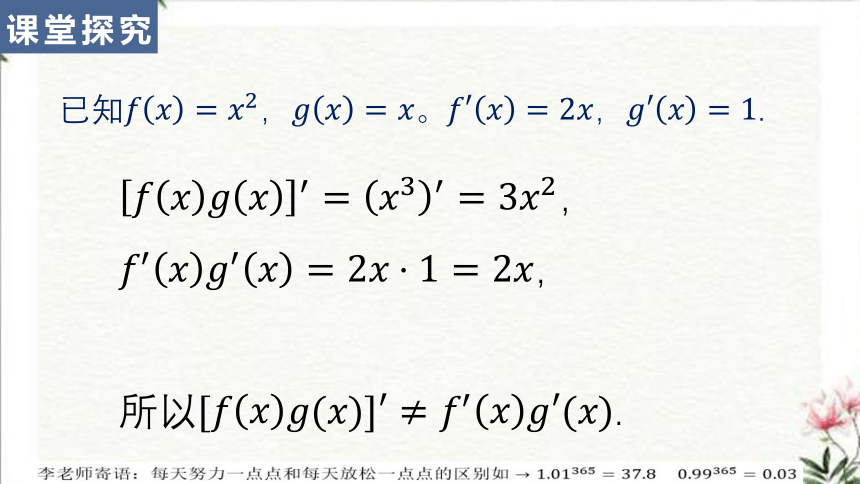

文档简介
第五章 一元函数的导数及其应用
5.2.2 导数的四则运算法则
使用教材:人教A版2019选择性必修第二册
授课教师:李祥老师
复习引入
基本初等函数的导数
1. 若????????=????????为常数,则????′????=0;
2.若 ????????=????????(α∈Q,且α≠0),则????′????=?????????????1;
3.若????????=sin????,则????′????=cos????;
4.若 ????????=cos????,则????′(????)=?sin????;
5.若 ????????=?????????(????>0, 且????≠1) ,则????′????=????????ln????;
特别地,若????????=e????,则????′????=e????;
6.若????????=log???????? (????>0, 且????≠1),则????′????=1????ln????;
特别地,若????????=ln????,则????′????=1????.
?
新课引入
如何求函数????????=????????+????的导数?
?
设????=?????=????2+????,由导数的定义,
??????????=(????+?????)2+????+??????(????2+????)?????
=(?????)2+2??????????+??????????=?????+2????+1,
所以?′????=lim?????→0??????????=2????+1.
?
观察????????=????2,????????=????,?????=????2+????;
与导数????′????=2????,????′????=1,?′(????)=2????+1.
你有什么发现和猜想?
?????=????????+????????;?′????=????′????+????′????.
猜想:[????????+????????]′=????′????+????′????.
同样地,?[?????????????????]′=????′(????)?????′????.
?
课堂探究
1.导数的运算法则1:
课堂探究
继续以????????=????2,????????=????,为例。????′????=2????,????′????=1.
你猜函数的积商关系和导数的积商关系是怎样的?
?
课堂探究
????????????????′=????2????′=????′=1,????′(????)????′(????)=2????1=2????.
所以????????????????′≠????′(????)????′(????).
?
已知????????=????2,????????=????。????′????=2????,????′????=1.
?
课堂探究
????????????????′=????3′=3????2,
????′????????′????=2?????1=2????,
所以[????????????(????)]′≠????′????????′(????).
?
已知????????=????2,????????=????。????′????=2????,????′????=1.
?
课堂探究
2.导数的运算法则2:
记三分钟
课堂探究
例题解析
例1 求导
例2 求导
例题解析
例1 求导数:
(1)????????=????3?????+3;(2)????????=2????+cos????;
解:(1)????′????=(????3?????+3)′=(????3)′?(????)′+(3)′
=3????2?1.?????????????????????
(2)????????′????=(2????+cos????)′=2????′+cos????′???????????????????????
=2????ln2?sin????.??
?
例2 求导数:
(1)????????=????3e????;??(2)????????=2sin????????2;
?
解:(1)????′????=????3e????′=(????3)′e????+????3(e????)′
=3????2e????+????3e????=3????2+????3e????.???
?
(2)????′(????)=2sin????????2′=2sin????′????2?2sin????(????2)′????4?????????????????=2cos?????????2?2sin?????2????????4???=2????cos?????4sin????????3??.???????????????????
?
例题解析
(4)?????=e????+????.
?
(5)?????=????2+2????????.
?
练习巩固
练习巩固
(4)?????′????=(e????+????)′=e????′+????′????=e????+12?????.??
?
5???????′(????)=[????2+2????????]′=????2+2????′????+????2+2????????′?
?????????????????????=2????+2?????+????2+2?????12????=5????2+6????2??????.??????????????????????????????????????????
?
练习巩固
练习巩固
练习巩固
练习巩固
练习巩固
作业1:名师导学
作业2:书本练习
作业3:
作业布置
5.2.2 导数的四则运算法则
使用教材:人教A版2019选择性必修第二册
授课教师:李祥老师
复习引入
基本初等函数的导数
1. 若????????=????????为常数,则????′????=0;
2.若 ????????=????????(α∈Q,且α≠0),则????′????=?????????????1;
3.若????????=sin????,则????′????=cos????;
4.若 ????????=cos????,则????′(????)=?sin????;
5.若 ????????=?????????(????>0, 且????≠1) ,则????′????=????????ln????;
特别地,若????????=e????,则????′????=e????;
6.若????????=log???????? (????>0, 且????≠1),则????′????=1????ln????;
特别地,若????????=ln????,则????′????=1????.
?
新课引入
如何求函数????????=????????+????的导数?
?
设????=?????=????2+????,由导数的定义,
??????????=(????+?????)2+????+??????(????2+????)?????
=(?????)2+2??????????+??????????=?????+2????+1,
所以?′????=lim?????→0??????????=2????+1.
?
观察????????=????2,????????=????,?????=????2+????;
与导数????′????=2????,????′????=1,?′(????)=2????+1.
你有什么发现和猜想?
?????=????????+????????;?′????=????′????+????′????.
猜想:[????????+????????]′=????′????+????′????.
同样地,?[?????????????????]′=????′(????)?????′????.
?
课堂探究
1.导数的运算法则1:
课堂探究
继续以????????=????2,????????=????,为例。????′????=2????,????′????=1.
你猜函数的积商关系和导数的积商关系是怎样的?
?
课堂探究
????????????????′=????2????′=????′=1,????′(????)????′(????)=2????1=2????.
所以????????????????′≠????′(????)????′(????).
?
已知????????=????2,????????=????。????′????=2????,????′????=1.
?
课堂探究
????????????????′=????3′=3????2,
????′????????′????=2?????1=2????,
所以[????????????(????)]′≠????′????????′(????).
?
已知????????=????2,????????=????。????′????=2????,????′????=1.
?
课堂探究
2.导数的运算法则2:
记三分钟
课堂探究
例题解析
例1 求导
例2 求导
例题解析
例1 求导数:
(1)????????=????3?????+3;(2)????????=2????+cos????;
解:(1)????′????=(????3?????+3)′=(????3)′?(????)′+(3)′
=3????2?1.?????????????????????
(2)????????′????=(2????+cos????)′=2????′+cos????′???????????????????????
=2????ln2?sin????.??
?
例2 求导数:
(1)????????=????3e????;??(2)????????=2sin????????2;
?
解:(1)????′????=????3e????′=(????3)′e????+????3(e????)′
=3????2e????+????3e????=3????2+????3e????.???
?
(2)????′(????)=2sin????????2′=2sin????′????2?2sin????(????2)′????4?????????????????=2cos?????????2?2sin?????2????????4???=2????cos?????4sin????????3??.???????????????????
?
例题解析
(4)?????=e????+????.
?
(5)?????=????2+2????????.
?
练习巩固
练习巩固
(4)?????′????=(e????+????)′=e????′+????′????=e????+12?????.??
?
5???????′(????)=[????2+2????????]′=????2+2????′????+????2+2????????′?
?????????????????????=2????+2?????+????2+2?????12????=5????2+6????2??????.??????????????????????????????????????????
?
练习巩固
练习巩固
练习巩固
练习巩固
练习巩固
作业1:名师导学
作业2:书本练习
作业3:
作业布置
