人教版(2019)数学必修第二册8_3_1棱柱、棱锥、棱台的表面积和体积课件(共33张PPT)
文档属性
| 名称 | 人教版(2019)数学必修第二册8_3_1棱柱、棱锥、棱台的表面积和体积课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 10:24:17 | ||
图片预览








文档简介
(共33张PPT)
1.3.1 柱体、椎体、台体的表面积与体积(1)
高一数学备课组
本节目标
1 .通过对棱柱、棱锥、棱台的研究,掌握棱柱、棱锥、
棱台的表面积与体积的求法.
2.会求棱柱、棱锥、棱台有关的组合体的表面积与体积.
课前预习
预习课本,思考并完成以下问题
1.棱柱、棱锥、棱台的表面积如何计算?
2.棱柱、棱锥、棱台的体积公式分别是什么?
课前小测
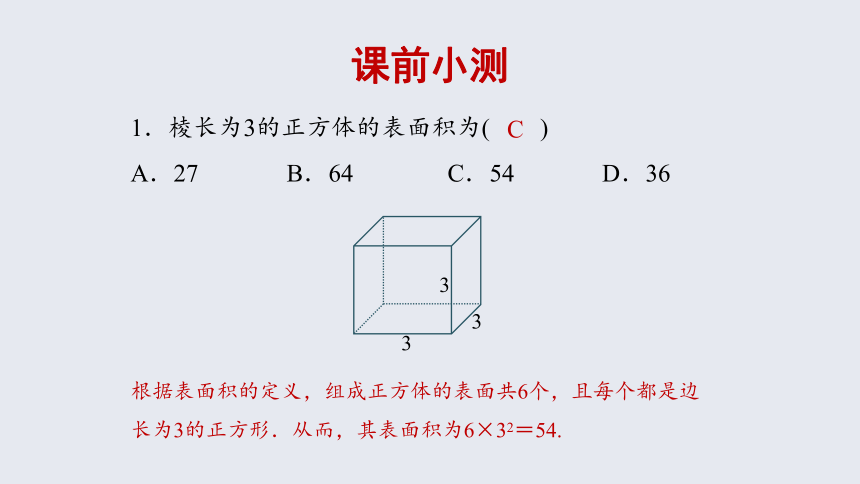
1.棱长为3的正方体的表面积为( )
A.27 B.64 C.54 D.36
3
3
3
根据表面积的定义,组成正方体的表面共6个,且每个都是边长为3的正方形.从而,其表面积为6×32=54.
C
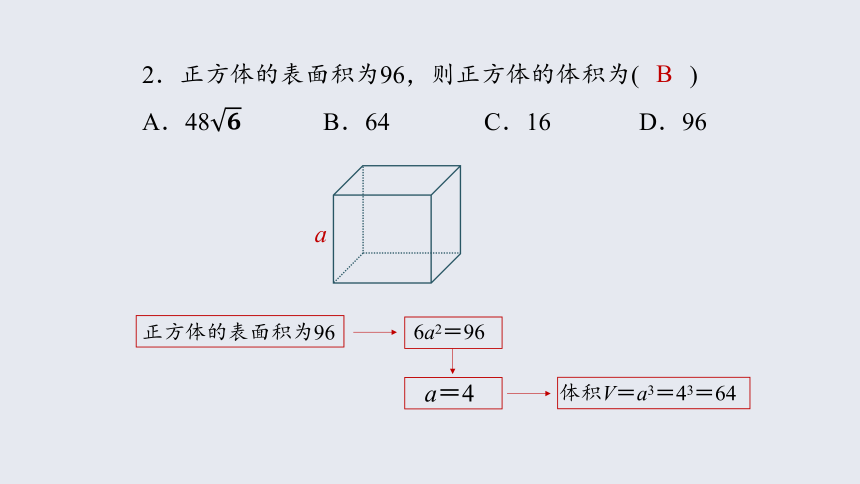
2.正方体的表面积为96,则正方体的体积为( )
A.48 B.64 C.16 D.96
a
正方体的表面积为96
6a2=96
a=4
体积V=a3=43=64
B
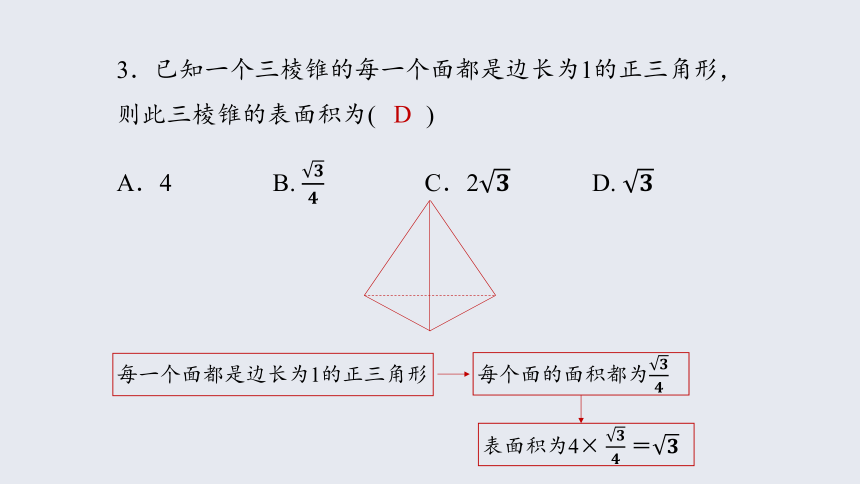
3.已知一个三棱锥的每一个面都是边长为1的正三角形,则此三棱锥的表面积为( )
A.4 B. C.2 D.
每个面的面积都为
每一个面都是边长为1的正三角形
表面积为4× =
D
4.已知棱台的上、下底面积分别为4, 16,高为3,则棱台的体积为________.
由棱台的体积公式可求得其体积为
V= (4+ +16)×3=28.
28
新知探究
1.棱柱、棱锥、棱台的侧面积与表面积
将棱柱、棱锥、棱台的侧面展开分别是平行四边形、若干个三角形、若干个梯形组成的平面图形,侧面展开图的面积就是棱柱、棱锥、棱台的侧面积.
棱柱、棱锥、棱台的表面积等于它们的侧面积与各自的底面积的和.
2.棱柱、棱锥、棱台的体积
棱柱:柱体的底面积为S,高为h,则V=Sh.
棱椎:椎体的底面积为S,高为h,则V= Sh.
棱台:台体的上、下底面面积为S,高为h,则
V= (+ +S)h.
注意
棱台的高是指两底面之间的距离,即从上底面上任意一点向下底面作垂线,这点与垂足之间的距离.
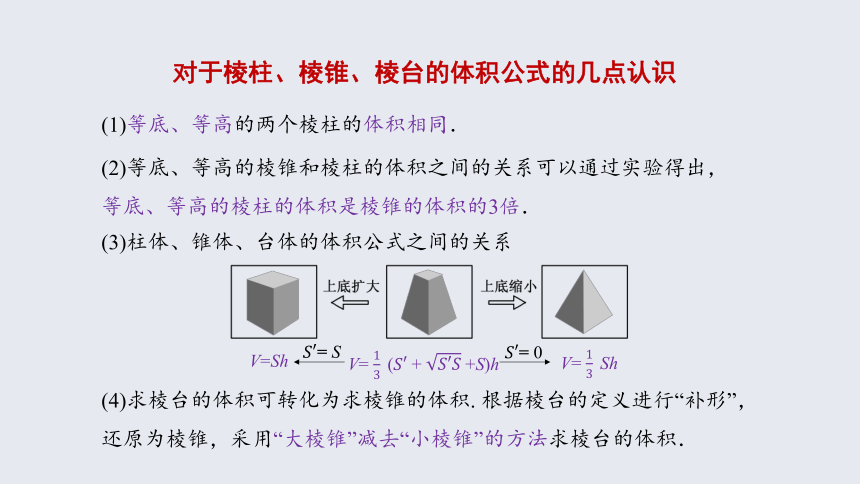
对于棱柱、棱锥、棱台的体积公式的几点认识
(1)等底、等高的两个棱柱的体积相同.
(2)等底、等高的棱锥和棱柱的体积之间的关系可以通过实验得出,等底、等高的棱柱的体积是棱锥的体积的3倍.
(3)柱体、锥体、台体的体积公式之间的关系
(4)求棱台的体积可转化为求棱锥的体积. 根据棱台的定义进行“补形”,还原为棱锥,采用“大棱锥”减去“小棱锥”的方法求棱台的体积.
V= (+ +S)h
= S
V=Sh
= 0
V= Sh
题型突破
典例深度剖析 重点多维探究
题型一 棱柱、棱锥、棱台的侧面积与表面积
[例1] 现有一个底面是菱形的直四棱柱,它的体对角线长为9和15,高是5,求该直四棱柱的侧面积.
9
15
5
如图,设底面对角线AC=a,BD=b,交点为O,对角线A1C=15,B1D=9,
∴a2+52=152,b2+52=92,
∴a2=200,b2=56.
∵该直四棱柱的底面是菱形,
∴AB2= = = =64,
∴AB=8.
∴直四棱柱的侧面积S=4×8×5=160.
[例1] 现有一个底面是菱形的直四棱柱,它的体对角线长为9和15,高是5,求该直四棱柱的侧面积.
9
15
5
技法点拨
注意
1
清楚各侧面的形状,求出每个侧面的面积.
2
求出其底面的面积.
3
求和得到表面积.
求棱柱、棱锥、棱台的表面积的基本步骤
组合体的表面积应注意重合部分的处理.
跟踪训练
1. 已知四棱台的上、下底面分别是边长为4和8的正方形,侧面是腰长为8的等腰梯形,则该四棱台的表面积为__________.
如图,在四棱台ABCD -A1B1C1D1中,过B1作B1F⊥BC,垂足为F,
在Rt△B1FB中,BF= ×(8-4)=2,B1B=8,
故B1F= =2,
所以S梯形BB1C1C= ×(8+4)×2=12,
故四棱台的侧面积S侧=4×12=48,
所以S表=48+4×4+8×8=80+48.
80+48
题型二 棱柱、棱锥、棱台的体积
[例2] (1)如图所示,正方体ABCD- A1B1C1D1的棱长为1,E为线段B1C上的一点,则三棱锥A -DED1的体积为______.
VA-DED1=VE -DD1A= × ×1×1×1=
(2)如图,某几何体下面部分为正方体ABCD- A′B′C′D′, 上面部分为正四棱锥S- ABCD,若几何体的高为5,棱AB=2,则该几何体的体积为________.
5
2
V=V正方体+VS- ABCD=12
V正方体=23=8
VS -ABCD=×22×(5-2)=4
12
(3) (全国卷Ⅲ)学生到工厂劳动实践,利用3D打印技术制作模型.如图,该模型为长方体ABCD -A1B1C1D1挖去四棱锥O-EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=6 cm,AA1=4 cm. 3D打印所用原料密度为0.9 g/cm3.不考虑打印损耗,制作该模型所需原料的质量为________g.
由题知挖去的四棱锥的底面是一个菱形,
对角线长分别为6 cm和4 cm,
故V挖去的四棱锥= × ×4×6×3=12(cm3).
又V长方体=6×6×4=144(cm3),
所以模型的体积为V长方体-V挖去的四棱锥=144-12=132(cm3),
所以制作该模型所需原料的质量为132×0.9=118.8(g).
118.8
技法点拨
求几何体体积的常用方法
跟踪训练
2.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积等于________ cm3.
V=VABC- A′B′C′-VM-ABC
=S△ABC·5- S△ABC·3
= ×3×4×5- × ×3×4×3
=30-6=24
还原
24
3.在长方体ABCD- A1B1C1D1中,截下一个棱锥C -A1DD1,求棱锥C -A1DD1的体积与剩余部分的体积之比.
设矩形ADD1A1的面积为S,AB=h,
∴VABCD- A1B1C1D1=VADD1A1- BCC1B1=Sh.
而棱锥C-A1DD1的底面积为S,高为h,
故三棱锥C- A1DD1的体积为:
VC -A1DD1= × S×h= Sh,
余下部分体积为:Sh- Sh= Sh.
所以棱锥C-A1DD1的体积与剩余部分的体积之比为1∶5.
题型三 棱台与棱锥之间关系的综合问题
[例3] 已知正四棱台(上、下底是正方形,上底面的中心在下底面的投影是下底面中心)上底面边长为6,高和下底面边长都是12,求它的侧面积.
6
12
12
如图,E,E1分别是BC,B1C1的中点,O,O1分别是下、上底面正方形的中心,则O1O为正四棱台的高,
则O1O=12. 连接OE,O1E1,
则OE= AB= ×12=6,O1E1= A1B1=3.
过E1作E1H⊥OE,垂足为H,
则E1H=O1O=12,OH=O1E1=3,
HE=OE-O1E1=6-3=3.
在Rt△E1HE中,E1E2=E1H2+HE2=122+32=32×17,
所以E1E=3.
所以S侧=4× ×(B1C1+BC)×E1E=2×(6+12)×3=108.
[例3] 已知正四棱台(上、下底是正方形,上底面的中心在下底面的投影是下底面中心)上底面边长为6,高和下底面边长都是12,求它的侧面积.
技法点拨
二是把正棱台还原成正棱锥,利用正棱锥的有关知识来解决.
解决有关正棱台的问题时,常用两种解题思路
一是把基本量转化到直角梯形中去解决;
跟踪训练
4. 在本例中,把棱台还原成棱锥,你能利用棱锥的有关知识求解吗?
如图,正四棱台的侧棱延长交于一点P.
取B1C1,BC的中点E1,E,则EE1的延长线必过P点.
O1,O分别是正方形A1B1C1D1与正方形ABCD的中心.
由正棱锥的定义,CC1的延长线过P点,
且有O1E1= A1B1=3,OE= AB=6,
则有= = ,
跟踪训练
4. 在本例中,把棱台还原成棱锥,你能利用棱锥的有关知识求解吗?
即= . 所以PO1=O1O=12.
在Rt△PO1E1中,
= +O1=122+32=32×17,
在Rt△POE中,
PE2=PO2+OE2=242+62=62×17,
所以E1E=PE-PE1=6-3=3.
所以S侧=4× ×(BC+B1C1)×E1E=2×(12+6)×3=108.
随堂检测
1.判断正误
(1)锥体的体积等于底面积与高之积.( )
(2)台体的体积,可转化为两个锥体体积之差.( )
(3)正方体的表面积为96,则正方体的体积为64.( )
×
√
√
2.如图所示,正方体ABCD -A1B1C1D1的棱长为1,则三棱锥D1 -ACD的体积是( )
A. B. C. D.1
三棱锥D1 -ADC的体积
V= S△ADC×D1D
= × ×AD×DC×D1D
= ×
=
A
3.已知高为3的棱柱ABC- A1B1C1的底面是边长为1的正三角形(如图),则三棱锥B1 -ABC的体积为( )
A. B. C. D.
D
3
1
1
1
VB1 -ABC= Sh = ××1×1×sin60°×3 =
4.把一个棱长为a的正方体,切成27个全等的小正方体,则所有小正方体的表面积为_________.
原正方体的棱长为a,切成的27个小正方体的棱长为a,每个小正方体的表面积S1= a2×6= a2,
所以27个小正方体的表面积是a2×27=18a2.
18a2
本课小结
1.棱柱、棱锥、棱台的表面积分别是它们侧面展开图的面积,因此弄清侧面展开图的形状及侧面展开图中各线段的长,是掌握它们的表面积有关问题的关键.
2.计算棱柱、棱锥、棱台的体积,关键是根据条件找出相应的底面面积和高,要充分运用多面体的有关截面,将空间问题转化为平面问题.
3.在几何体的体积计算中,注意体会“分割思想”、“补体思想”及“等价转化思想”.
1.3.1 柱体、椎体、台体的表面积与体积(1)
高一数学备课组
本节目标
1 .通过对棱柱、棱锥、棱台的研究,掌握棱柱、棱锥、
棱台的表面积与体积的求法.
2.会求棱柱、棱锥、棱台有关的组合体的表面积与体积.
课前预习
预习课本,思考并完成以下问题
1.棱柱、棱锥、棱台的表面积如何计算?
2.棱柱、棱锥、棱台的体积公式分别是什么?
课前小测
1.棱长为3的正方体的表面积为( )
A.27 B.64 C.54 D.36
3
3
3
根据表面积的定义,组成正方体的表面共6个,且每个都是边长为3的正方形.从而,其表面积为6×32=54.
C
2.正方体的表面积为96,则正方体的体积为( )
A.48 B.64 C.16 D.96
a
正方体的表面积为96
6a2=96
a=4
体积V=a3=43=64
B
3.已知一个三棱锥的每一个面都是边长为1的正三角形,则此三棱锥的表面积为( )
A.4 B. C.2 D.
每个面的面积都为
每一个面都是边长为1的正三角形
表面积为4× =
D
4.已知棱台的上、下底面积分别为4, 16,高为3,则棱台的体积为________.
由棱台的体积公式可求得其体积为
V= (4+ +16)×3=28.
28
新知探究
1.棱柱、棱锥、棱台的侧面积与表面积
将棱柱、棱锥、棱台的侧面展开分别是平行四边形、若干个三角形、若干个梯形组成的平面图形,侧面展开图的面积就是棱柱、棱锥、棱台的侧面积.
棱柱、棱锥、棱台的表面积等于它们的侧面积与各自的底面积的和.
2.棱柱、棱锥、棱台的体积
棱柱:柱体的底面积为S,高为h,则V=Sh.
棱椎:椎体的底面积为S,高为h,则V= Sh.
棱台:台体的上、下底面面积为S,高为h,则
V= (+ +S)h.
注意
棱台的高是指两底面之间的距离,即从上底面上任意一点向下底面作垂线,这点与垂足之间的距离.
对于棱柱、棱锥、棱台的体积公式的几点认识
(1)等底、等高的两个棱柱的体积相同.
(2)等底、等高的棱锥和棱柱的体积之间的关系可以通过实验得出,等底、等高的棱柱的体积是棱锥的体积的3倍.
(3)柱体、锥体、台体的体积公式之间的关系
(4)求棱台的体积可转化为求棱锥的体积. 根据棱台的定义进行“补形”,还原为棱锥,采用“大棱锥”减去“小棱锥”的方法求棱台的体积.
V= (+ +S)h
= S
V=Sh
= 0
V= Sh
题型突破
典例深度剖析 重点多维探究
题型一 棱柱、棱锥、棱台的侧面积与表面积
[例1] 现有一个底面是菱形的直四棱柱,它的体对角线长为9和15,高是5,求该直四棱柱的侧面积.
9
15
5
如图,设底面对角线AC=a,BD=b,交点为O,对角线A1C=15,B1D=9,
∴a2+52=152,b2+52=92,
∴a2=200,b2=56.
∵该直四棱柱的底面是菱形,
∴AB2= = = =64,
∴AB=8.
∴直四棱柱的侧面积S=4×8×5=160.
[例1] 现有一个底面是菱形的直四棱柱,它的体对角线长为9和15,高是5,求该直四棱柱的侧面积.
9
15
5
技法点拨
注意
1
清楚各侧面的形状,求出每个侧面的面积.
2
求出其底面的面积.
3
求和得到表面积.
求棱柱、棱锥、棱台的表面积的基本步骤
组合体的表面积应注意重合部分的处理.
跟踪训练
1. 已知四棱台的上、下底面分别是边长为4和8的正方形,侧面是腰长为8的等腰梯形,则该四棱台的表面积为__________.
如图,在四棱台ABCD -A1B1C1D1中,过B1作B1F⊥BC,垂足为F,
在Rt△B1FB中,BF= ×(8-4)=2,B1B=8,
故B1F= =2,
所以S梯形BB1C1C= ×(8+4)×2=12,
故四棱台的侧面积S侧=4×12=48,
所以S表=48+4×4+8×8=80+48.
80+48
题型二 棱柱、棱锥、棱台的体积
[例2] (1)如图所示,正方体ABCD- A1B1C1D1的棱长为1,E为线段B1C上的一点,则三棱锥A -DED1的体积为______.
VA-DED1=VE -DD1A= × ×1×1×1=
(2)如图,某几何体下面部分为正方体ABCD- A′B′C′D′, 上面部分为正四棱锥S- ABCD,若几何体的高为5,棱AB=2,则该几何体的体积为________.
5
2
V=V正方体+VS- ABCD=12
V正方体=23=8
VS -ABCD=×22×(5-2)=4
12
(3) (全国卷Ⅲ)学生到工厂劳动实践,利用3D打印技术制作模型.如图,该模型为长方体ABCD -A1B1C1D1挖去四棱锥O-EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=6 cm,AA1=4 cm. 3D打印所用原料密度为0.9 g/cm3.不考虑打印损耗,制作该模型所需原料的质量为________g.
由题知挖去的四棱锥的底面是一个菱形,
对角线长分别为6 cm和4 cm,
故V挖去的四棱锥= × ×4×6×3=12(cm3).
又V长方体=6×6×4=144(cm3),
所以模型的体积为V长方体-V挖去的四棱锥=144-12=132(cm3),
所以制作该模型所需原料的质量为132×0.9=118.8(g).
118.8
技法点拨
求几何体体积的常用方法
跟踪训练
2.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积等于________ cm3.
V=VABC- A′B′C′-VM-ABC
=S△ABC·5- S△ABC·3
= ×3×4×5- × ×3×4×3
=30-6=24
还原
24
3.在长方体ABCD- A1B1C1D1中,截下一个棱锥C -A1DD1,求棱锥C -A1DD1的体积与剩余部分的体积之比.
设矩形ADD1A1的面积为S,AB=h,
∴VABCD- A1B1C1D1=VADD1A1- BCC1B1=Sh.
而棱锥C-A1DD1的底面积为S,高为h,
故三棱锥C- A1DD1的体积为:
VC -A1DD1= × S×h= Sh,
余下部分体积为:Sh- Sh= Sh.
所以棱锥C-A1DD1的体积与剩余部分的体积之比为1∶5.
题型三 棱台与棱锥之间关系的综合问题
[例3] 已知正四棱台(上、下底是正方形,上底面的中心在下底面的投影是下底面中心)上底面边长为6,高和下底面边长都是12,求它的侧面积.
6
12
12
如图,E,E1分别是BC,B1C1的中点,O,O1分别是下、上底面正方形的中心,则O1O为正四棱台的高,
则O1O=12. 连接OE,O1E1,
则OE= AB= ×12=6,O1E1= A1B1=3.
过E1作E1H⊥OE,垂足为H,
则E1H=O1O=12,OH=O1E1=3,
HE=OE-O1E1=6-3=3.
在Rt△E1HE中,E1E2=E1H2+HE2=122+32=32×17,
所以E1E=3.
所以S侧=4× ×(B1C1+BC)×E1E=2×(6+12)×3=108.
[例3] 已知正四棱台(上、下底是正方形,上底面的中心在下底面的投影是下底面中心)上底面边长为6,高和下底面边长都是12,求它的侧面积.
技法点拨
二是把正棱台还原成正棱锥,利用正棱锥的有关知识来解决.
解决有关正棱台的问题时,常用两种解题思路
一是把基本量转化到直角梯形中去解决;
跟踪训练
4. 在本例中,把棱台还原成棱锥,你能利用棱锥的有关知识求解吗?
如图,正四棱台的侧棱延长交于一点P.
取B1C1,BC的中点E1,E,则EE1的延长线必过P点.
O1,O分别是正方形A1B1C1D1与正方形ABCD的中心.
由正棱锥的定义,CC1的延长线过P点,
且有O1E1= A1B1=3,OE= AB=6,
则有= = ,
跟踪训练
4. 在本例中,把棱台还原成棱锥,你能利用棱锥的有关知识求解吗?
即= . 所以PO1=O1O=12.
在Rt△PO1E1中,
= +O1=122+32=32×17,
在Rt△POE中,
PE2=PO2+OE2=242+62=62×17,
所以E1E=PE-PE1=6-3=3.
所以S侧=4× ×(BC+B1C1)×E1E=2×(12+6)×3=108.
随堂检测
1.判断正误
(1)锥体的体积等于底面积与高之积.( )
(2)台体的体积,可转化为两个锥体体积之差.( )
(3)正方体的表面积为96,则正方体的体积为64.( )
×
√
√
2.如图所示,正方体ABCD -A1B1C1D1的棱长为1,则三棱锥D1 -ACD的体积是( )
A. B. C. D.1
三棱锥D1 -ADC的体积
V= S△ADC×D1D
= × ×AD×DC×D1D
= ×
=
A
3.已知高为3的棱柱ABC- A1B1C1的底面是边长为1的正三角形(如图),则三棱锥B1 -ABC的体积为( )
A. B. C. D.
D
3
1
1
1
VB1 -ABC= Sh = ××1×1×sin60°×3 =
4.把一个棱长为a的正方体,切成27个全等的小正方体,则所有小正方体的表面积为_________.
原正方体的棱长为a,切成的27个小正方体的棱长为a,每个小正方体的表面积S1= a2×6= a2,
所以27个小正方体的表面积是a2×27=18a2.
18a2
本课小结
1.棱柱、棱锥、棱台的表面积分别是它们侧面展开图的面积,因此弄清侧面展开图的形状及侧面展开图中各线段的长,是掌握它们的表面积有关问题的关键.
2.计算棱柱、棱锥、棱台的体积,关键是根据条件找出相应的底面面积和高,要充分运用多面体的有关截面,将空间问题转化为平面问题.
3.在几何体的体积计算中,注意体会“分割思想”、“补体思想”及“等价转化思想”.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
