2.5.1 二次函数与一元二次方程的关系 课件(共24张PPT)
文档属性
| 名称 | 2.5.1 二次函数与一元二次方程的关系 课件(共24张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
北师版九年级下册 二次函数
§2.5.1 二次函数与一元二次方程
1.经历探索二次函数与一元二次方程关系的过程, 体会二者之间的联系;
2.理解掌握二次函数图象与x轴交点的个数与一元二次方程的根的
个数之间的三种关系,以及方程根与交点横坐标的对应关系;(重点)
3.理解两种函数(含二次函数)图象的交点问题的相关解法,以及
二次函数与不等式之间的问题思考范式.(难点)
温故知新
1.一元二次方程ax2+bx+c=0 的求根公式是什么?
当b2-4ac≥0时,
当b2-4ac<0时,方程无实数根.
2.解下列一元二次方程:
(1)x2+2x=0 (2)x2-2x+1=0 (3)x2-2x+2=0.
解:(1)x1=0, x2=-2.
(2)x1=x2=1.
(3)没有实数根.
温故知新
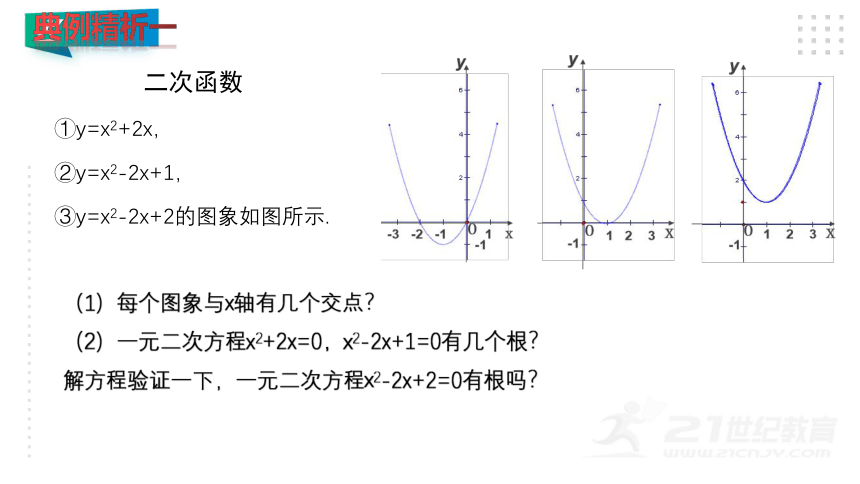
我们已经知道,竖直上抛物体的高度 h (m) 与运动时间t(s)的关系可以用公式
h=-5t2+v0t +h0 表示,
其中h0 (m)是抛出点距地面的高度,v0 (m/s)
是抛出时的速度.一个小球从地面被
以40 m/s的速度竖直向上抛起,小球的
高度h (m)与运动时间t(s)的关系如图所示,
那么
(1)h与t 的关系式是什么?
(2)小球经过多少秒后落地?
你有几种求解方法?与同伴交流.
h/m
t/s
1 2 3 4 5 6 7 8
80
70
60
50
40
30
20
10
情境导入
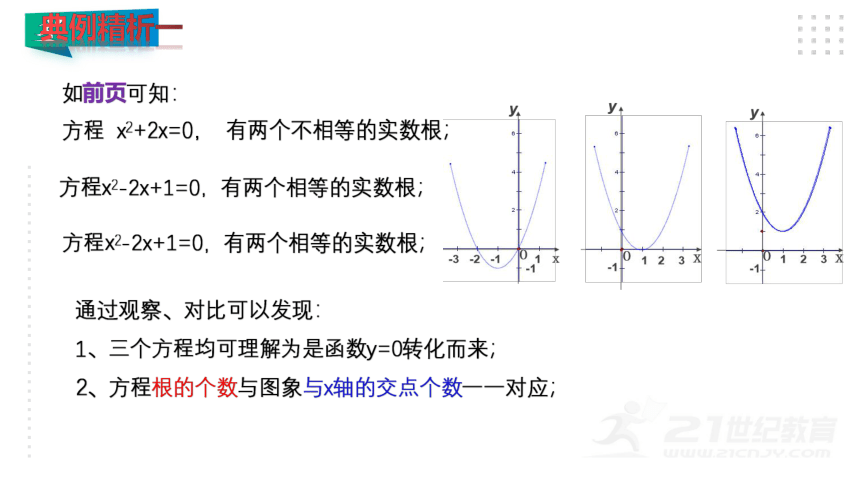
二次函数
①y=x2+2x,
②y=x2-2x+1,
③y=x2-2x+2的图象如图所示.
(1)每个图象与x轴有几个交点?
(2)一元二次方程x2+2x=0,x2-2x+1=0有几个根?
解方程验证一下,一元二次方程x2-2x+2=0有根吗?
典例精析一
如前页可知:
方程 x2+2x=0, 有两个不相等的实数根;
方程x2-2x+1=0,有两个相等的实数根;
方程x2-2x+1=0,有两个相等的实数根;
通过观察、对比可以发现:
1、三个方程均可理解为是函数y=0转化而来;
2、方程根的个数与图象与x轴的交点个数一一对应;
典例精析一
一、方程根的个数与图象和x轴的交点个数间关系.
小结:
1、b2-4ac>0,方程有两个不等实数根 对应函数图象与x轴有两个交点;
2、b2-4ac=0,方程有两个相等实数根 对应函数图象与x轴有一个交点;
3、b2-4ac<0, 方程有没有 实数根 对应函数图象与x轴没有交点.
二、二次函数 y=ax2+bx+c 的图象和x轴的交点的横坐标与 一元二次方程ax2+bx+c=0 的根有什么关系?
1、方程x2+2x=0(根为0、-2)
2、x2-2x+1=0(根为1)
3、方程x2-2x+1=0(无根)
交点横坐标分别为0、-2;
交点横坐标分别为1;
小结:二次函数图象与x轴的交点横坐标即是
对应一元二次方程的两个根。
小结:
我们已经知道,竖直上抛物体的高度 h (m) 与运动时间t(s)的关系可以用公式h=-5t2+v0t +h0 表示,
其中h0 (m)是抛出点距地面的高度,v0 (m/s)
是抛出时的速度.一个小球从地面被
以40 m/s的速度竖直向上抛起,小球的
高度h (m)与运动时间t(s)的关系如图所示,
那么
(1)h与t 的关系式是什么?
(2)小球经过多少秒后落地?
你有几种求解方法?与同伴交流.
h=-5t2+40t+h0
8秒
方法一:落地时,h=h0=0,∴-5t2+40t=0 t=0或8
问题反思
1.小兰画了一个函数y=x2+ax+b的图象如图,则关于x的方程x2+ax+b=0的解是( )
A.无解 B.x=1
C.x=-4 D.x=-1或x=4
跟踪练习
D
2.抛物线y=-3x2-x+4与x轴的交点个数是( )
A.0 B.1
C.2 D.以上都不对
C
3.二次函数y=2x2+mx+8的图象如图所示,则m的值是( )
A.-8 B.8
C.±8 D.6
B
b2-4ac=0
4.已知一元二次方程x2+x-2=0有两个不相等的实数根
x1=1,x2=-2,则二次函数y=x2+x-2与x轴的交点坐标为 .
(1,0),(-2,0)
跟踪练习
合作共学
1.抛物线y=2x2-3x+1与坐标轴的交点个数是( )
A.0 B.1 C.2 D.3
【变式】 (2019·荆门)抛物线y=-x2+4x-4与坐标轴的交点个数为( )
A.0 B.1 C.2 D.3
D
C
特别注意:“坐标轴”指代x,y两轴.
3.若函数y=(a-1)x2-4x+2a的图象与x轴有且只有一个交点,则a的值为 .
-1或2或1
解析:通过观察表达式,可以发现二次项系数不确定,所以可以分
(1)a=0;(2)a≠0 两类情况讨论
(1)当a=1时,原函数为y=-4x+2,其图像与x轴交于(0.5,0),一个点;
(2) 当a≠1 时,函数为二次函数,若与x轴交于一点,则由b2-4ac=0
解得:a=-1或2.
合作共学
4.已知二次函数y=ax2+bx的图象如图.若一元二次方程ax2+bx+k=0有实数解,则k的最小值为( )
A.-4 B.-6
C.-8 D.0
A
解析:通过对比观察,可以发现方程其实就是二次函数y=y=ax2+bx中,y=-k时
转化而来.而 y=-k 是一个常函数,其图像大致如上图所示,若想要二次方程有解,
则两个函数图象必须有交点。据此可以发现k最小为-4
合作共学
典例精析二
1、二次函数y=-x2+3x十4的图象与一次函数y=2x—1的图象相交吗 如果相交,请求出它们的交点坐称.
解析:以往我们在学习两个一次函数图象相交问题时,强调过——两个函数的图象
交点坐标就是由两个函数关系式联立,组成的方程组(或二次方程)的公共解.
解:令2x-1=-x2+3x十4
整理得:x2-x-5=0
2.已知直线l:y=kx+1与抛物线y=x2-4x.
(1)求证:直线l与该拋物线总有两个交点;
(2)设直线l与该抛物线两交点为A,B,O为原点,当k=-2时,求△OAB的面积.
解:(1)证明:令x2-4x=kx+1,则x2-(4+k)x-1=0.
∵Δ=(4+k)2+4>0,
∴直线l与该抛物线总有两个交点.
典例精析二
(2)设点A,B的坐标分别为(x1,y1)(x2,y2),直线l与y轴交点为C(0,1).
由(1)知x1+x2=4+k=2,x1x2=-1.
∴(x1-x2)2=(x1+x2)2-4x1x2=4+4=8.
∴|x1-x2|=2√2.
∴S△OAB=· OC·|x1-x2|= ×1×2√2=2√2 .
典例精析二
1.(2019·新乡一模)如果函数y=-2x与函数y=ax2+1有两个不同的交点,则实数a的取值范围是 .
跟踪练习
a<1且a≠0
2、如图,已知二次函数y=-x2+2x+3.
请写出该函数的三条性质.
解:如图所示.答案不唯一,如:
①抛物线与x轴交于点(-1,0)和(3,0);
②与y轴交于点(0,3);③当-1<x<3时,y>0;
④对称轴为直线x=1;⑤顶点坐标为(1,4).
令 -2x=ax2+1 则ax2+2x+1=0
b2-4ac>0且a≠0
抛物线y=ax +bx+c(a≠0)的部分图象如图所示,与x轴的一个交点坐标为(4.0);抛物线的对称轴是x=1.
下列结论中∶
①abc>0;②2a+b=0;③方程ax +bx+c=3有两个不相等的实数根
④抛物线与x轴的另一个交点坐标为(-2,0)
⑤若点A(m,n)在该抛物线上,则
am + bm十 c ≤a+b十c.
其中正确的有( )
A.5个 B.4个 C.3个 D.2个
典例精析三
【解析】
①∵对称轴在y轴的右侧,∴ab<0,
抛物线与y轴交于正半轴,∴c>0, ∴abc<0, 故①错误;
∵对称轴为x=1,∴b=-2a,2a+b=0, 故②正确;
由图象得∶y=3时,与抛物线有两个交点,
∴方程ac +bx+c=3有两个不相等的实数根;故③正确;
∵抛物线与x轴的一个交点坐标为(4,0),抛物线的对称轴是x=1,
∴抛物线与x轴的另一个交点坐标为(-2,0).故④正确;
∵抛物线的对称轴是x=1,y有最大值是a+b+C,
又∵点A(m,n)在该抛物线上,∴am +bm+c≤a+b+c,故⑤正确
1.(天津.中考) 已知抛物线y=ax2+bx+c(a,b,c为常数,a≠0)经过点(-1,0),(0,3),其对称轴在y轴右侧,有下列结论:
①抛物线经过点(1,0);②方程ax2+bx+c=2有两个不相等的实数根;
③.-3<a+b<3。其中,正确结论的个数为( )
A. 0 B. 1 C. 2 D. 3
课堂练习
C
2.(甘肃白银.中考)(3分)如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;
④a+b≥m(am+b)(m为实数);
⑤当﹣1<x<3时,y>0,其中正确的是 。
课堂练习
①②④
1.理解了二次函数y=ax2+bx+c的图象与x轴的交点的横坐标就是一元二次方程ax2+bx+c=0的根;
2.学习了二次方程根与二次函数图象与x交点个数的三种情况;
3、学习了常函数(y=k)和一次函数与二次函数图象相交时的各类问题的解法.
北师版九年级下册 二次函数
§2.5.1 二次函数与一元二次方程
1.经历探索二次函数与一元二次方程关系的过程, 体会二者之间的联系;
2.理解掌握二次函数图象与x轴交点的个数与一元二次方程的根的
个数之间的三种关系,以及方程根与交点横坐标的对应关系;(重点)
3.理解两种函数(含二次函数)图象的交点问题的相关解法,以及
二次函数与不等式之间的问题思考范式.(难点)
温故知新
1.一元二次方程ax2+bx+c=0 的求根公式是什么?
当b2-4ac≥0时,
当b2-4ac<0时,方程无实数根.
2.解下列一元二次方程:
(1)x2+2x=0 (2)x2-2x+1=0 (3)x2-2x+2=0.
解:(1)x1=0, x2=-2.
(2)x1=x2=1.
(3)没有实数根.
温故知新
我们已经知道,竖直上抛物体的高度 h (m) 与运动时间t(s)的关系可以用公式
h=-5t2+v0t +h0 表示,
其中h0 (m)是抛出点距地面的高度,v0 (m/s)
是抛出时的速度.一个小球从地面被
以40 m/s的速度竖直向上抛起,小球的
高度h (m)与运动时间t(s)的关系如图所示,
那么
(1)h与t 的关系式是什么?
(2)小球经过多少秒后落地?
你有几种求解方法?与同伴交流.
h/m
t/s
1 2 3 4 5 6 7 8
80
70
60
50
40
30
20
10
情境导入
二次函数
①y=x2+2x,
②y=x2-2x+1,
③y=x2-2x+2的图象如图所示.
(1)每个图象与x轴有几个交点?
(2)一元二次方程x2+2x=0,x2-2x+1=0有几个根?
解方程验证一下,一元二次方程x2-2x+2=0有根吗?
典例精析一
如前页可知:
方程 x2+2x=0, 有两个不相等的实数根;
方程x2-2x+1=0,有两个相等的实数根;
方程x2-2x+1=0,有两个相等的实数根;
通过观察、对比可以发现:
1、三个方程均可理解为是函数y=0转化而来;
2、方程根的个数与图象与x轴的交点个数一一对应;
典例精析一
一、方程根的个数与图象和x轴的交点个数间关系.
小结:
1、b2-4ac>0,方程有两个不等实数根 对应函数图象与x轴有两个交点;
2、b2-4ac=0,方程有两个相等实数根 对应函数图象与x轴有一个交点;
3、b2-4ac<0, 方程有没有 实数根 对应函数图象与x轴没有交点.
二、二次函数 y=ax2+bx+c 的图象和x轴的交点的横坐标与 一元二次方程ax2+bx+c=0 的根有什么关系?
1、方程x2+2x=0(根为0、-2)
2、x2-2x+1=0(根为1)
3、方程x2-2x+1=0(无根)
交点横坐标分别为0、-2;
交点横坐标分别为1;
小结:二次函数图象与x轴的交点横坐标即是
对应一元二次方程的两个根。
小结:
我们已经知道,竖直上抛物体的高度 h (m) 与运动时间t(s)的关系可以用公式h=-5t2+v0t +h0 表示,
其中h0 (m)是抛出点距地面的高度,v0 (m/s)
是抛出时的速度.一个小球从地面被
以40 m/s的速度竖直向上抛起,小球的
高度h (m)与运动时间t(s)的关系如图所示,
那么
(1)h与t 的关系式是什么?
(2)小球经过多少秒后落地?
你有几种求解方法?与同伴交流.
h=-5t2+40t+h0
8秒
方法一:落地时,h=h0=0,∴-5t2+40t=0 t=0或8
问题反思
1.小兰画了一个函数y=x2+ax+b的图象如图,则关于x的方程x2+ax+b=0的解是( )
A.无解 B.x=1
C.x=-4 D.x=-1或x=4
跟踪练习
D
2.抛物线y=-3x2-x+4与x轴的交点个数是( )
A.0 B.1
C.2 D.以上都不对
C
3.二次函数y=2x2+mx+8的图象如图所示,则m的值是( )
A.-8 B.8
C.±8 D.6
B
b2-4ac=0
4.已知一元二次方程x2+x-2=0有两个不相等的实数根
x1=1,x2=-2,则二次函数y=x2+x-2与x轴的交点坐标为 .
(1,0),(-2,0)
跟踪练习
合作共学
1.抛物线y=2x2-3x+1与坐标轴的交点个数是( )
A.0 B.1 C.2 D.3
【变式】 (2019·荆门)抛物线y=-x2+4x-4与坐标轴的交点个数为( )
A.0 B.1 C.2 D.3
D
C
特别注意:“坐标轴”指代x,y两轴.
3.若函数y=(a-1)x2-4x+2a的图象与x轴有且只有一个交点,则a的值为 .
-1或2或1
解析:通过观察表达式,可以发现二次项系数不确定,所以可以分
(1)a=0;(2)a≠0 两类情况讨论
(1)当a=1时,原函数为y=-4x+2,其图像与x轴交于(0.5,0),一个点;
(2) 当a≠1 时,函数为二次函数,若与x轴交于一点,则由b2-4ac=0
解得:a=-1或2.
合作共学
4.已知二次函数y=ax2+bx的图象如图.若一元二次方程ax2+bx+k=0有实数解,则k的最小值为( )
A.-4 B.-6
C.-8 D.0
A
解析:通过对比观察,可以发现方程其实就是二次函数y=y=ax2+bx中,y=-k时
转化而来.而 y=-k 是一个常函数,其图像大致如上图所示,若想要二次方程有解,
则两个函数图象必须有交点。据此可以发现k最小为-4
合作共学
典例精析二
1、二次函数y=-x2+3x十4的图象与一次函数y=2x—1的图象相交吗 如果相交,请求出它们的交点坐称.
解析:以往我们在学习两个一次函数图象相交问题时,强调过——两个函数的图象
交点坐标就是由两个函数关系式联立,组成的方程组(或二次方程)的公共解.
解:令2x-1=-x2+3x十4
整理得:x2-x-5=0
2.已知直线l:y=kx+1与抛物线y=x2-4x.
(1)求证:直线l与该拋物线总有两个交点;
(2)设直线l与该抛物线两交点为A,B,O为原点,当k=-2时,求△OAB的面积.
解:(1)证明:令x2-4x=kx+1,则x2-(4+k)x-1=0.
∵Δ=(4+k)2+4>0,
∴直线l与该抛物线总有两个交点.
典例精析二
(2)设点A,B的坐标分别为(x1,y1)(x2,y2),直线l与y轴交点为C(0,1).
由(1)知x1+x2=4+k=2,x1x2=-1.
∴(x1-x2)2=(x1+x2)2-4x1x2=4+4=8.
∴|x1-x2|=2√2.
∴S△OAB=· OC·|x1-x2|= ×1×2√2=2√2 .
典例精析二
1.(2019·新乡一模)如果函数y=-2x与函数y=ax2+1有两个不同的交点,则实数a的取值范围是 .
跟踪练习
a<1且a≠0
2、如图,已知二次函数y=-x2+2x+3.
请写出该函数的三条性质.
解:如图所示.答案不唯一,如:
①抛物线与x轴交于点(-1,0)和(3,0);
②与y轴交于点(0,3);③当-1<x<3时,y>0;
④对称轴为直线x=1;⑤顶点坐标为(1,4).
令 -2x=ax2+1 则ax2+2x+1=0
b2-4ac>0且a≠0
抛物线y=ax +bx+c(a≠0)的部分图象如图所示,与x轴的一个交点坐标为(4.0);抛物线的对称轴是x=1.
下列结论中∶
①abc>0;②2a+b=0;③方程ax +bx+c=3有两个不相等的实数根
④抛物线与x轴的另一个交点坐标为(-2,0)
⑤若点A(m,n)在该抛物线上,则
am + bm十 c ≤a+b十c.
其中正确的有( )
A.5个 B.4个 C.3个 D.2个
典例精析三
【解析】
①∵对称轴在y轴的右侧,∴ab<0,
抛物线与y轴交于正半轴,∴c>0, ∴abc<0, 故①错误;
∵对称轴为x=1,∴b=-2a,2a+b=0, 故②正确;
由图象得∶y=3时,与抛物线有两个交点,
∴方程ac +bx+c=3有两个不相等的实数根;故③正确;
∵抛物线与x轴的一个交点坐标为(4,0),抛物线的对称轴是x=1,
∴抛物线与x轴的另一个交点坐标为(-2,0).故④正确;
∵抛物线的对称轴是x=1,y有最大值是a+b+C,
又∵点A(m,n)在该抛物线上,∴am +bm+c≤a+b+c,故⑤正确
1.(天津.中考) 已知抛物线y=ax2+bx+c(a,b,c为常数,a≠0)经过点(-1,0),(0,3),其对称轴在y轴右侧,有下列结论:
①抛物线经过点(1,0);②方程ax2+bx+c=2有两个不相等的实数根;
③.-3<a+b<3。其中,正确结论的个数为( )
A. 0 B. 1 C. 2 D. 3
课堂练习
C
2.(甘肃白银.中考)(3分)如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;
④a+b≥m(am+b)(m为实数);
⑤当﹣1<x<3时,y>0,其中正确的是 。
课堂练习
①②④
1.理解了二次函数y=ax2+bx+c的图象与x轴的交点的横坐标就是一元二次方程ax2+bx+c=0的根;
2.学习了二次方程根与二次函数图象与x交点个数的三种情况;
3、学习了常函数(y=k)和一次函数与二次函数图象相交时的各类问题的解法.
