8.3 动能和动能定理练习(Word版,含解析)
文档属性
| 名称 | 8.3 动能和动能定理练习(Word版,含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 199.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-11-23 14:37:44 | ||
图片预览



文档简介
动能和动能定理
基础练
1.关于动能定理,下列说法正确的是( )
A.某过程中合力的总功等于各力做功的绝对值之和
B.只要合力对物体做功,物体的动能就一定改变
C.在物体动能不改变的过程中,动能定理不适用
D.动能定理只适用于受恒力作用而加速运动的过程
2.在水平路面上,有一辆以36 km/h的速度行驶的客车,在车厢后座有一位乘客甲,把一个质量为4 kg的行李以相对客车5 m/s的速度抛给前方座位的另一位乘客乙,则以地面为参考系行李的动能和以客车为参考系行李的动能分别是( )
A.200 J 50 J
B.450 J 50 J
C.50 J 50 J
D.450 J 450 J
3.一质量为m的小球,用长为l的轻绳悬挂于O点。小球在水平拉力F作用下,从平衡位置P点很缓慢地移动到Q点,如图所示,则拉力F所做的功为( )
A.mglcos θ
B.mgl(1-cos θ)
C.Flcos θ
D.Flsin θ
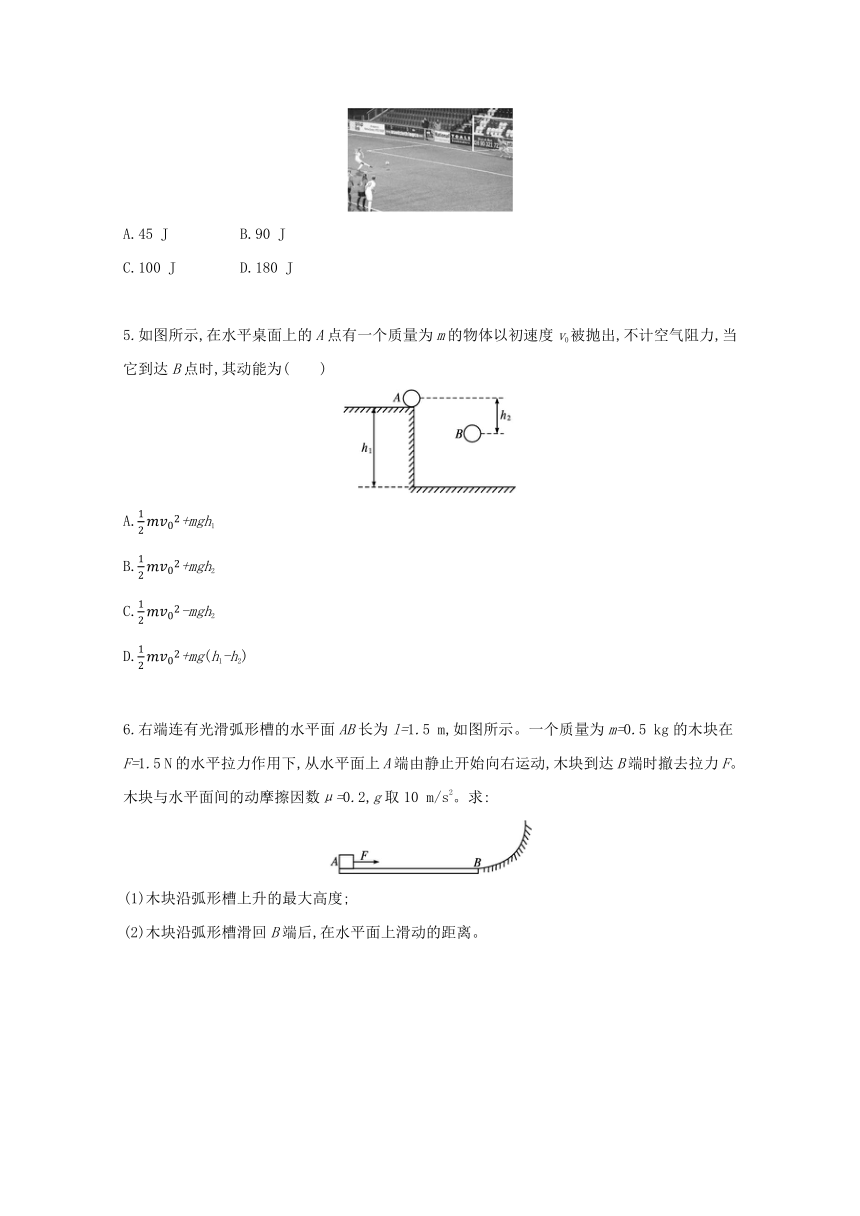
4.如图所示,某一足球比赛中,运动员大力踢出的点球恰好击中横梁。假定足球击中横梁时速度大小为20 m/s,足球的质量为450 g,球门高度约为2.4 m,不计空气阻力,则该运动员对足球所做的功的大小约为( )(g取10 m/s2)
A.45 J B.90 J
C.100 J D.180 J
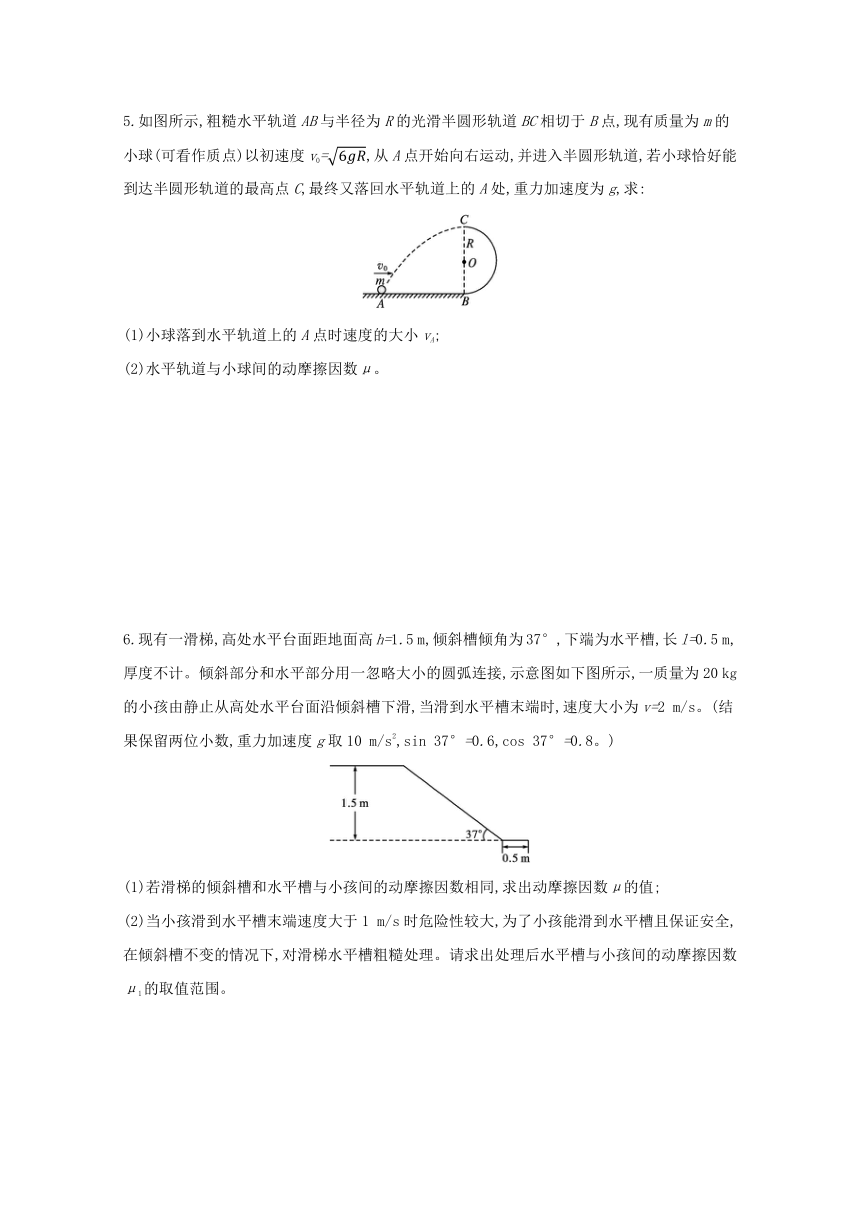
5.如图所示,在水平桌面上的A点有一个质量为m的物体以初速度v0被抛出,不计空气阻力,当它到达B点时,其动能为( )
A.+mgh1
B.+mgh2
C.-mgh2
D.+mg(h1-h2)
6.右端连有光滑弧形槽的水平面AB长为l=1.5 m,如图所示。一个质量为m=0.5 kg的木块在F=1.5 N的水平拉力作用下,从水平面上A端由静止开始向右运动,木块到达B端时撤去拉力F。木块与水平面间的动摩擦因数μ=0.2,g取10 m/s2。求:
(1)木块沿弧形槽上升的最大高度;
(2)木块沿弧形槽滑回B端后,在水平面上滑动的距离。
7.如图所示,质量为m的小球自由下落d后,沿竖直面内的固定轨道ABC运动,AB段是半径为d的光滑圆弧,BC段是直径为d的粗糙半圆弧(B是轨道的最低点)。小球恰好能运动到C点。(重力加速度为g)求:
(1)小球运动到B处时对轨道的压力大小;
(2)小球在BC上运动过程中,摩擦力对小球做的功。
提升练
1.连接A、B两点的弧形轨道ACB和ADB关于A、B的连线对称,轨道材料相同,粗糙程度相同,如图所示,一个小物块由A点以一定的初速度v开始沿ACB轨道到达B点的速度为v1;若由A以大小相同的初速度v沿ADB轨道到达B点的速度为v2。v1和v2的大小关系为( )
A.v1>v2
B.v1=v2
C.v1D.条件不足,无法判定
2.物体在合力作用下做直线运动的v-t图像如图所示,下列表述正确的是( )
A.在0~1 s内,合力做正功
B.在0~2 s内,合力总是做负功
C.在1~2 s内,合力不做功
D.在0~3 s内,合力总是做正功
3.(多选)如图所示,质量为m的物体在水平恒力F的推动下,从山坡底部A处由静止开始运动至高为h的坡顶B处,获得的速度为v,A、B间的水平距离为s,下列说法正确的是( )
A.物体克服重力所做的功是mgh
B.合力对物体做的功是mv2
C.推力对物体做的功是Fs-mgh
D.物体克服阻力做的功是mv2+mgh-Fs
4.如图所示,一半径为R的半圆形轨道竖直固定放置,轨道两端等高;质量为m的质点自轨道端点P由静止开始滑下,滑到最低点Q时,对轨道的正压力为2mg,重力加速度为g。质点自P滑到Q的过程中,克服摩擦力所做的功为( )
A.mgR B.mgR
C.mgR D.mgR
5.如图所示,粗糙水平轨道AB与半径为R的光滑半圆形轨道BC相切于B点,现有质量为m的小球(可看作质点)以初速度v0=,从A点开始向右运动,并进入半圆形轨道,若小球恰好能到达半圆形轨道的最高点C,最终又落回水平轨道上的A处,重力加速度为g,求:
(1)小球落到水平轨道上的A点时速度的大小vA;
(2)水平轨道与小球间的动摩擦因数μ。
6.现有一滑梯,高处水平台面距地面高h=1.5 m,倾斜槽倾角为37°,下端为水平槽,长l=0.5 m,厚度不计。倾斜部分和水平部分用一忽略大小的圆弧连接,示意图如下图所示,一质量为20 kg的小孩由静止从高处水平台面沿倾斜槽下滑,当滑到水平槽末端时,速度大小为v=2 m/s。(结果保留两位小数,重力加速度g取10 m/s2,sin 37°=0.6,cos 37°=0.8。)
(1)若滑梯的倾斜槽和水平槽与小孩间的动摩擦因数相同,求出动摩擦因数μ的值;
(2)当小孩滑到水平槽末端速度大于1 m/s时危险性较大,为了小孩能滑到水平槽且保证安全,在倾斜槽不变的情况下,对滑梯水平槽粗糙处理。请求出处理后水平槽与小孩间的动摩擦因数μ1的取值范围。
参考答案:
基础练
1.关于动能定理,下列说法正确的是( )
A.某过程中合力的总功等于各力做功的绝对值之和
B.只要合力对物体做功,物体的动能就一定改变
C.在物体动能不改变的过程中,动能定理不适用
D.动能定理只适用于受恒力作用而加速运动的过程
解析:公式W=ΔEk中,W为合力做的功,也可以是各力做功的代数和,A错误,B正确;动能不变,只能说明合力做的总功W=0,动能定理仍适用,C错误;动能定理既适用于恒力做功,也可适用于变力做功,D项错误。
答案:B
2.在水平路面上,有一辆以36 km/h的速度行驶的客车,在车厢后座有一位乘客甲,把一个质量为4 kg的行李以相对客车5 m/s的速度抛给前方座位的另一位乘客乙,则以地面为参考系行李的动能和以客车为参考系行李的动能分别是( )
A.200 J 50 J
B.450 J 50 J
C.50 J 50 J
D.450 J 450 J
解析:行李相对地面的速度v=v车+v相对=15m/s,所以行李的动能Ek=mv2=450J。行李相对客车的速度v'=5m/s,所以行李的动能Ek'=mv'2=50J。
答案:B
3.一质量为m的小球,用长为l的轻绳悬挂于O点。小球在水平拉力F作用下,从平衡位置P点很缓慢地移动到Q点,如图所示,则拉力F所做的功为( )
A.mglcos θ
B.mgl(1-cos θ)
C.Flcos θ
D.Flsin θ
解析:小球缓慢移动,时时都处于平衡状态,由平衡条件可知,F=mgtanθ,随着θ的增大,F也在增大,F是一个变化的力,不能直接用功的公式求它做的功,所以此题需要用动能定理求解。由于物体缓慢移动,动能保持不变,由动能定理得-mgl(1-cosθ)+W=0,所以W=mgl(1-cosθ),B正确。
答案:B
4.如图所示,某一足球比赛中,运动员大力踢出的点球恰好击中横梁。假定足球击中横梁时速度大小为20 m/s,足球的质量为450 g,球门高度约为2.4 m,不计空气阻力,则该运动员对足球所做的功的大小约为( )(g取10 m/s2)
A.45 J B.90 J
C.100 J D.180 J
解析:球门高度约为h=2.4m,对足球从运动员踢球到击中横梁的过程,根据动能定理得W-mgh=mv2-0,则W=mgh+mv2=0.45×10×2.4J+×0.45×202J=100.8J≈100J。
答案:C
5.如图所示,在水平桌面上的A点有一个质量为m的物体以初速度v0被抛出,不计空气阻力,当它到达B点时,其动能为( )
A.+mgh1
B.+mgh2
C.-mgh2
D.+mg(h1-h2)
解析:由A到B,合力对物体做的功W=mgh2,物体的动能变化ΔEk=Ek-,根据动能定理得物体在B点的动能Ek=+mgh2,B正确。
答案:B
6.右端连有光滑弧形槽的水平面AB长为l=1.5 m,如图所示。一个质量为m=0.5 kg的木块在F=1.5 N的水平拉力作用下,从水平面上A端由静止开始向右运动,木块到达B端时撤去拉力F。木块与水平面间的动摩擦因数μ=0.2,g取10 m/s2。求:
(1)木块沿弧形槽上升的最大高度;
(2)木块沿弧形槽滑回B端后,在水平面上滑动的距离。
解析:(1)设木块沿弧形槽上升的最大高度为h,对木块由A端运动到最大高度的过程,由动能定理得Fl-μmgl-mgh=0
解得h==0.15m。
(2)设木块沿弧形槽滑回B端后在水平面上滑行的距离为s,由动能定理得
mgh-μmgs=0
解得s==0.75m。
答案:(1)0.15 m (2)0.75 m
7.如图所示,质量为m的小球自由下落d后,沿竖直面内的固定轨道ABC运动,AB段是半径为d的光滑圆弧,BC段是直径为d的粗糙半圆弧(B是轨道的最低点)。小球恰好能运动到C点。(重力加速度为g)求:
(1)小球运动到B处时对轨道的压力大小;
(2)小球在BC上运动过程中,摩擦力对小球做的功。
解析:(1)小球下落到B的过程由动能定理得
2mgd=mv2,
在B点FN-mg=m,得FN=5mg,
根据牛顿第三定律得,FN'=FN=5mg。
(2)在C点,mg=m。小球从B运动到C的过程
-mgd+Wf=mv2,得Wf=-mgd。
答案:(1)5mg (2)-mgd
提升练
1.连接A、B两点的弧形轨道ACB和ADB关于A、B的连线对称,轨道材料相同,粗糙程度相同,如图所示,一个小物块由A点以一定的初速度v开始沿ACB轨道到达B点的速度为v1;若由A以大小相同的初速度v沿ADB轨道到达B点的速度为v2。v1和v2的大小关系为( )
A.v1>v2
B.v1=v2
C.v1D.条件不足,无法判定
解析:弧形轨道ACB和ADB的长度相等,物块与两轨道间的动摩擦因数相同,物块在上面运动可认为做圆周运动,则物块在ADB上运动时对曲面的正压力大于在ACB上运动时对曲面的正压力,故在ADB上摩擦力做的功大于在ACB上摩擦力做的功,再由动能定理得出选项A正确。
答案:A
2.物体在合力作用下做直线运动的v-t图像如图所示,下列表述正确的是( )
A.在0~1 s内,合力做正功
B.在0~2 s内,合力总是做负功
C.在1~2 s内,合力不做功
D.在0~3 s内,合力总是做正功
解析:由v-t图知,0~1s内,v增加,动能增加,由动能定理可知合力做正功,A正确;1~2s内,v减小,动能减小,合力做负功,0~2s内合力先做正功,后做负功,整个过程做正功;0~3s内合力先做正功,后做负功,整个过程做功为零,B、C、D错误。
答案:A
3.(多选)如图所示,质量为m的物体在水平恒力F的推动下,从山坡底部A处由静止开始运动至高为h的坡顶B处,获得的速度为v,A、B间的水平距离为s,下列说法正确的是( )
A.物体克服重力所做的功是mgh
B.合力对物体做的功是mv2
C.推力对物体做的功是Fs-mgh
D.物体克服阻力做的功是mv2+mgh-Fs
解析:设物体克服阻力做的功为W,由动能定理得Fs-mgh-W=mv2-0,得W=Fs-mgh-mv2,故D错误;因为F是水平恒力,s是水平位移,推力对物体做的功可由W=Fs计算,故C错误;由动能定理知,B正确;物体克服重力所做的功为mgh,A正确。
答案:AB
4.如图所示,一半径为R的半圆形轨道竖直固定放置,轨道两端等高;质量为m的质点自轨道端点P由静止开始滑下,滑到最低点Q时,对轨道的正压力为2mg,重力加速度为g。质点自P滑到Q的过程中,克服摩擦力所做的功为( )
A.mgR B.mgR
C.mgR D.mgR
解析:在Q点质点受到竖直向下的重力和竖直向上的支持力,两力的合力充当向心力,所以有FN-mg=m,FN=2mg,联立解得v=。质点自P滑到Q的过程中,重力做正功,摩擦力做负功,根据动能定理可得mgR-Wf=mv2,解得Wf=mgR,所以质点克服摩擦力做功mgR,C正确。
答案:C
5.如图所示,粗糙水平轨道AB与半径为R的光滑半圆形轨道BC相切于B点,现有质量为m的小球(可看作质点)以初速度v0=,从A点开始向右运动,并进入半圆形轨道,若小球恰好能到达半圆形轨道的最高点C,最终又落回水平轨道上的A处,重力加速度为g,求:
(1)小球落到水平轨道上的A点时速度的大小vA;
(2)水平轨道与小球间的动摩擦因数μ。
解析:(1)由mg=m,得vC=,
从C到A由动能定理得
mg·2R=,得vA=。
(2)AB的距离为xAB=vCt==2R
从A出发回到A由动能定理得
-μmgxAB=,得μ=0.25。
答案:(1)
(2)0.25
6.现有一滑梯,高处水平台面距地面高h=1.5 m,倾斜槽倾角为37°,下端为水平槽,长l=0.5 m,厚度不计。倾斜部分和水平部分用一忽略大小的圆弧连接,示意图如下图所示,一质量为20 kg的小孩由静止从高处水平台面沿倾斜槽下滑,当滑到水平槽末端时,速度大小为v=2 m/s。(结果保留两位小数,重力加速度g取10 m/s2,sin 37°=0.6,cos 37°=0.8。)
(1)若滑梯的倾斜槽和水平槽与小孩间的动摩擦因数相同,求出动摩擦因数μ的值;
(2)当小孩滑到水平槽末端速度大于1 m/s时危险性较大,为了小孩能滑到水平槽且保证安全,在倾斜槽不变的情况下,对滑梯水平槽粗糙处理。请求出处理后水平槽与小孩间的动摩擦因数μ1的取值范围。
解析:(1)研究小孩的整个运动过程,利用动能定理得
mgh-μmgcos37°×-μmgl=mv2
解得μ=0.52。
(2)由题意可知小孩到达水平槽末端时的速度v'应小于等于1m/s,小孩到达斜槽末端的速度为v1,利用动能定理,在倾斜槽上有
mgh-μmgcos37°×
在水平槽上有mv'2-=-μ1mgl
联立得μ1=0.82
所以μ1≥0.82。
答案:(1)0.52
(2)μ1≥0.82
基础练
1.关于动能定理,下列说法正确的是( )
A.某过程中合力的总功等于各力做功的绝对值之和
B.只要合力对物体做功,物体的动能就一定改变
C.在物体动能不改变的过程中,动能定理不适用
D.动能定理只适用于受恒力作用而加速运动的过程
2.在水平路面上,有一辆以36 km/h的速度行驶的客车,在车厢后座有一位乘客甲,把一个质量为4 kg的行李以相对客车5 m/s的速度抛给前方座位的另一位乘客乙,则以地面为参考系行李的动能和以客车为参考系行李的动能分别是( )
A.200 J 50 J
B.450 J 50 J
C.50 J 50 J
D.450 J 450 J
3.一质量为m的小球,用长为l的轻绳悬挂于O点。小球在水平拉力F作用下,从平衡位置P点很缓慢地移动到Q点,如图所示,则拉力F所做的功为( )
A.mglcos θ
B.mgl(1-cos θ)
C.Flcos θ
D.Flsin θ
4.如图所示,某一足球比赛中,运动员大力踢出的点球恰好击中横梁。假定足球击中横梁时速度大小为20 m/s,足球的质量为450 g,球门高度约为2.4 m,不计空气阻力,则该运动员对足球所做的功的大小约为( )(g取10 m/s2)
A.45 J B.90 J
C.100 J D.180 J
5.如图所示,在水平桌面上的A点有一个质量为m的物体以初速度v0被抛出,不计空气阻力,当它到达B点时,其动能为( )
A.+mgh1
B.+mgh2
C.-mgh2
D.+mg(h1-h2)
6.右端连有光滑弧形槽的水平面AB长为l=1.5 m,如图所示。一个质量为m=0.5 kg的木块在F=1.5 N的水平拉力作用下,从水平面上A端由静止开始向右运动,木块到达B端时撤去拉力F。木块与水平面间的动摩擦因数μ=0.2,g取10 m/s2。求:
(1)木块沿弧形槽上升的最大高度;
(2)木块沿弧形槽滑回B端后,在水平面上滑动的距离。
7.如图所示,质量为m的小球自由下落d后,沿竖直面内的固定轨道ABC运动,AB段是半径为d的光滑圆弧,BC段是直径为d的粗糙半圆弧(B是轨道的最低点)。小球恰好能运动到C点。(重力加速度为g)求:
(1)小球运动到B处时对轨道的压力大小;
(2)小球在BC上运动过程中,摩擦力对小球做的功。
提升练
1.连接A、B两点的弧形轨道ACB和ADB关于A、B的连线对称,轨道材料相同,粗糙程度相同,如图所示,一个小物块由A点以一定的初速度v开始沿ACB轨道到达B点的速度为v1;若由A以大小相同的初速度v沿ADB轨道到达B点的速度为v2。v1和v2的大小关系为( )
A.v1>v2
B.v1=v2
C.v1
2.物体在合力作用下做直线运动的v-t图像如图所示,下列表述正确的是( )
A.在0~1 s内,合力做正功
B.在0~2 s内,合力总是做负功
C.在1~2 s内,合力不做功
D.在0~3 s内,合力总是做正功
3.(多选)如图所示,质量为m的物体在水平恒力F的推动下,从山坡底部A处由静止开始运动至高为h的坡顶B处,获得的速度为v,A、B间的水平距离为s,下列说法正确的是( )
A.物体克服重力所做的功是mgh
B.合力对物体做的功是mv2
C.推力对物体做的功是Fs-mgh
D.物体克服阻力做的功是mv2+mgh-Fs
4.如图所示,一半径为R的半圆形轨道竖直固定放置,轨道两端等高;质量为m的质点自轨道端点P由静止开始滑下,滑到最低点Q时,对轨道的正压力为2mg,重力加速度为g。质点自P滑到Q的过程中,克服摩擦力所做的功为( )
A.mgR B.mgR
C.mgR D.mgR
5.如图所示,粗糙水平轨道AB与半径为R的光滑半圆形轨道BC相切于B点,现有质量为m的小球(可看作质点)以初速度v0=,从A点开始向右运动,并进入半圆形轨道,若小球恰好能到达半圆形轨道的最高点C,最终又落回水平轨道上的A处,重力加速度为g,求:
(1)小球落到水平轨道上的A点时速度的大小vA;
(2)水平轨道与小球间的动摩擦因数μ。
6.现有一滑梯,高处水平台面距地面高h=1.5 m,倾斜槽倾角为37°,下端为水平槽,长l=0.5 m,厚度不计。倾斜部分和水平部分用一忽略大小的圆弧连接,示意图如下图所示,一质量为20 kg的小孩由静止从高处水平台面沿倾斜槽下滑,当滑到水平槽末端时,速度大小为v=2 m/s。(结果保留两位小数,重力加速度g取10 m/s2,sin 37°=0.6,cos 37°=0.8。)
(1)若滑梯的倾斜槽和水平槽与小孩间的动摩擦因数相同,求出动摩擦因数μ的值;
(2)当小孩滑到水平槽末端速度大于1 m/s时危险性较大,为了小孩能滑到水平槽且保证安全,在倾斜槽不变的情况下,对滑梯水平槽粗糙处理。请求出处理后水平槽与小孩间的动摩擦因数μ1的取值范围。
参考答案:
基础练
1.关于动能定理,下列说法正确的是( )
A.某过程中合力的总功等于各力做功的绝对值之和
B.只要合力对物体做功,物体的动能就一定改变
C.在物体动能不改变的过程中,动能定理不适用
D.动能定理只适用于受恒力作用而加速运动的过程
解析:公式W=ΔEk中,W为合力做的功,也可以是各力做功的代数和,A错误,B正确;动能不变,只能说明合力做的总功W=0,动能定理仍适用,C错误;动能定理既适用于恒力做功,也可适用于变力做功,D项错误。
答案:B
2.在水平路面上,有一辆以36 km/h的速度行驶的客车,在车厢后座有一位乘客甲,把一个质量为4 kg的行李以相对客车5 m/s的速度抛给前方座位的另一位乘客乙,则以地面为参考系行李的动能和以客车为参考系行李的动能分别是( )
A.200 J 50 J
B.450 J 50 J
C.50 J 50 J
D.450 J 450 J
解析:行李相对地面的速度v=v车+v相对=15m/s,所以行李的动能Ek=mv2=450J。行李相对客车的速度v'=5m/s,所以行李的动能Ek'=mv'2=50J。
答案:B
3.一质量为m的小球,用长为l的轻绳悬挂于O点。小球在水平拉力F作用下,从平衡位置P点很缓慢地移动到Q点,如图所示,则拉力F所做的功为( )
A.mglcos θ
B.mgl(1-cos θ)
C.Flcos θ
D.Flsin θ
解析:小球缓慢移动,时时都处于平衡状态,由平衡条件可知,F=mgtanθ,随着θ的增大,F也在增大,F是一个变化的力,不能直接用功的公式求它做的功,所以此题需要用动能定理求解。由于物体缓慢移动,动能保持不变,由动能定理得-mgl(1-cosθ)+W=0,所以W=mgl(1-cosθ),B正确。
答案:B
4.如图所示,某一足球比赛中,运动员大力踢出的点球恰好击中横梁。假定足球击中横梁时速度大小为20 m/s,足球的质量为450 g,球门高度约为2.4 m,不计空气阻力,则该运动员对足球所做的功的大小约为( )(g取10 m/s2)
A.45 J B.90 J
C.100 J D.180 J
解析:球门高度约为h=2.4m,对足球从运动员踢球到击中横梁的过程,根据动能定理得W-mgh=mv2-0,则W=mgh+mv2=0.45×10×2.4J+×0.45×202J=100.8J≈100J。
答案:C
5.如图所示,在水平桌面上的A点有一个质量为m的物体以初速度v0被抛出,不计空气阻力,当它到达B点时,其动能为( )
A.+mgh1
B.+mgh2
C.-mgh2
D.+mg(h1-h2)
解析:由A到B,合力对物体做的功W=mgh2,物体的动能变化ΔEk=Ek-,根据动能定理得物体在B点的动能Ek=+mgh2,B正确。
答案:B
6.右端连有光滑弧形槽的水平面AB长为l=1.5 m,如图所示。一个质量为m=0.5 kg的木块在F=1.5 N的水平拉力作用下,从水平面上A端由静止开始向右运动,木块到达B端时撤去拉力F。木块与水平面间的动摩擦因数μ=0.2,g取10 m/s2。求:
(1)木块沿弧形槽上升的最大高度;
(2)木块沿弧形槽滑回B端后,在水平面上滑动的距离。
解析:(1)设木块沿弧形槽上升的最大高度为h,对木块由A端运动到最大高度的过程,由动能定理得Fl-μmgl-mgh=0
解得h==0.15m。
(2)设木块沿弧形槽滑回B端后在水平面上滑行的距离为s,由动能定理得
mgh-μmgs=0
解得s==0.75m。
答案:(1)0.15 m (2)0.75 m
7.如图所示,质量为m的小球自由下落d后,沿竖直面内的固定轨道ABC运动,AB段是半径为d的光滑圆弧,BC段是直径为d的粗糙半圆弧(B是轨道的最低点)。小球恰好能运动到C点。(重力加速度为g)求:
(1)小球运动到B处时对轨道的压力大小;
(2)小球在BC上运动过程中,摩擦力对小球做的功。
解析:(1)小球下落到B的过程由动能定理得
2mgd=mv2,
在B点FN-mg=m,得FN=5mg,
根据牛顿第三定律得,FN'=FN=5mg。
(2)在C点,mg=m。小球从B运动到C的过程
-mgd+Wf=mv2,得Wf=-mgd。
答案:(1)5mg (2)-mgd
提升练
1.连接A、B两点的弧形轨道ACB和ADB关于A、B的连线对称,轨道材料相同,粗糙程度相同,如图所示,一个小物块由A点以一定的初速度v开始沿ACB轨道到达B点的速度为v1;若由A以大小相同的初速度v沿ADB轨道到达B点的速度为v2。v1和v2的大小关系为( )
A.v1>v2
B.v1=v2
C.v1
解析:弧形轨道ACB和ADB的长度相等,物块与两轨道间的动摩擦因数相同,物块在上面运动可认为做圆周运动,则物块在ADB上运动时对曲面的正压力大于在ACB上运动时对曲面的正压力,故在ADB上摩擦力做的功大于在ACB上摩擦力做的功,再由动能定理得出选项A正确。
答案:A
2.物体在合力作用下做直线运动的v-t图像如图所示,下列表述正确的是( )
A.在0~1 s内,合力做正功
B.在0~2 s内,合力总是做负功
C.在1~2 s内,合力不做功
D.在0~3 s内,合力总是做正功
解析:由v-t图知,0~1s内,v增加,动能增加,由动能定理可知合力做正功,A正确;1~2s内,v减小,动能减小,合力做负功,0~2s内合力先做正功,后做负功,整个过程做正功;0~3s内合力先做正功,后做负功,整个过程做功为零,B、C、D错误。
答案:A
3.(多选)如图所示,质量为m的物体在水平恒力F的推动下,从山坡底部A处由静止开始运动至高为h的坡顶B处,获得的速度为v,A、B间的水平距离为s,下列说法正确的是( )
A.物体克服重力所做的功是mgh
B.合力对物体做的功是mv2
C.推力对物体做的功是Fs-mgh
D.物体克服阻力做的功是mv2+mgh-Fs
解析:设物体克服阻力做的功为W,由动能定理得Fs-mgh-W=mv2-0,得W=Fs-mgh-mv2,故D错误;因为F是水平恒力,s是水平位移,推力对物体做的功可由W=Fs计算,故C错误;由动能定理知,B正确;物体克服重力所做的功为mgh,A正确。
答案:AB
4.如图所示,一半径为R的半圆形轨道竖直固定放置,轨道两端等高;质量为m的质点自轨道端点P由静止开始滑下,滑到最低点Q时,对轨道的正压力为2mg,重力加速度为g。质点自P滑到Q的过程中,克服摩擦力所做的功为( )
A.mgR B.mgR
C.mgR D.mgR
解析:在Q点质点受到竖直向下的重力和竖直向上的支持力,两力的合力充当向心力,所以有FN-mg=m,FN=2mg,联立解得v=。质点自P滑到Q的过程中,重力做正功,摩擦力做负功,根据动能定理可得mgR-Wf=mv2,解得Wf=mgR,所以质点克服摩擦力做功mgR,C正确。
答案:C
5.如图所示,粗糙水平轨道AB与半径为R的光滑半圆形轨道BC相切于B点,现有质量为m的小球(可看作质点)以初速度v0=,从A点开始向右运动,并进入半圆形轨道,若小球恰好能到达半圆形轨道的最高点C,最终又落回水平轨道上的A处,重力加速度为g,求:
(1)小球落到水平轨道上的A点时速度的大小vA;
(2)水平轨道与小球间的动摩擦因数μ。
解析:(1)由mg=m,得vC=,
从C到A由动能定理得
mg·2R=,得vA=。
(2)AB的距离为xAB=vCt==2R
从A出发回到A由动能定理得
-μmgxAB=,得μ=0.25。
答案:(1)
(2)0.25
6.现有一滑梯,高处水平台面距地面高h=1.5 m,倾斜槽倾角为37°,下端为水平槽,长l=0.5 m,厚度不计。倾斜部分和水平部分用一忽略大小的圆弧连接,示意图如下图所示,一质量为20 kg的小孩由静止从高处水平台面沿倾斜槽下滑,当滑到水平槽末端时,速度大小为v=2 m/s。(结果保留两位小数,重力加速度g取10 m/s2,sin 37°=0.6,cos 37°=0.8。)
(1)若滑梯的倾斜槽和水平槽与小孩间的动摩擦因数相同,求出动摩擦因数μ的值;
(2)当小孩滑到水平槽末端速度大于1 m/s时危险性较大,为了小孩能滑到水平槽且保证安全,在倾斜槽不变的情况下,对滑梯水平槽粗糙处理。请求出处理后水平槽与小孩间的动摩擦因数μ1的取值范围。
解析:(1)研究小孩的整个运动过程,利用动能定理得
mgh-μmgcos37°×-μmgl=mv2
解得μ=0.52。
(2)由题意可知小孩到达水平槽末端时的速度v'应小于等于1m/s,小孩到达斜槽末端的速度为v1,利用动能定理,在倾斜槽上有
mgh-μmgcos37°×
在水平槽上有mv'2-=-μ1mgl
联立得μ1=0.82
所以μ1≥0.82。
答案:(1)0.52
(2)μ1≥0.82
