2021-2022学年苏科版八年级数学上册 3.3勾股定理的简单应用 同步达标测评 (word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学上册 3.3勾股定理的简单应用 同步达标测评 (word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 327.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 19:01:45 | ||
图片预览


文档简介
2021-2022学年苏科版八年级数学上册《3.3勾股定理的简单应用》同步达标测评(附答案)
一.选择题
1.如图,一块三角形木板,测得AB=13,BC=5,AC=12,则三角形木板ABC的面积为( )
A.60 B.30 C.65 D.不能确定
2.如图,在一个高为3米,长为5米的楼梯表面铺地毯,则地毯长度为( )米
A.4米 B.5米 C.7米 D.8米
3.人在平地上以1.5米/秒的速度向东走了80秒,接着以2米/秒的速度向南走了45秒,这时他离开出发点( )
A.180米 B.150米 C.120米 D.100米
4.如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M表示的实数为( )
A.5 B. C. D.
5.国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口A处出发先往东走8km,又往北走2km,遇到障碍后又往西走3km,再向北走到6km处往东拐,仅走了1km,就找到了宝藏,则门口A到藏宝点B的直线距离是( )
A.20km B.14km C.11km D.10km
6.小明同学先向北行进千米,然后向东进千米,再向北行进千米,最后又向东行进一定距离,此时小明离出发点的距离是千米,小明最后向东行进了( )
A.3千米 B.4千米
C.5千米 D.6千米
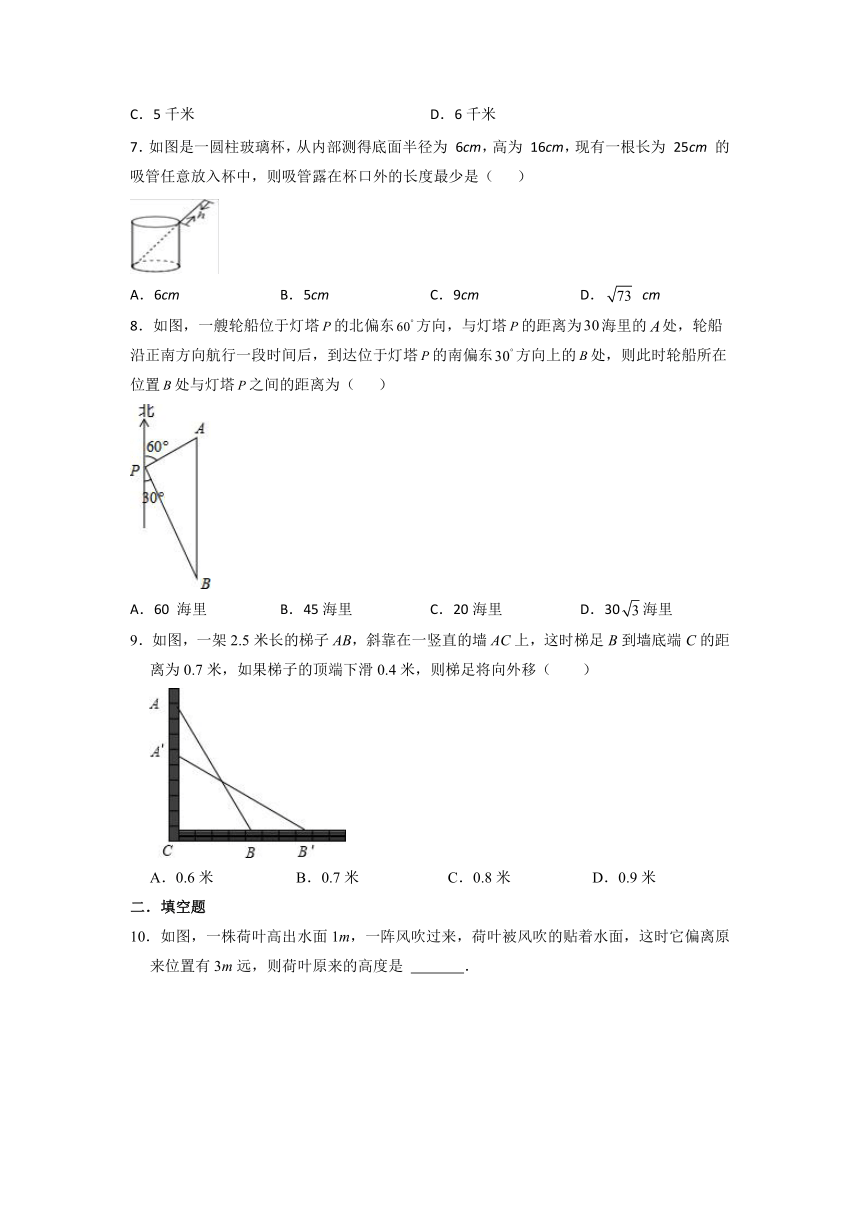
7.如图是一圆柱玻璃杯,从内部测得底面半径为 6cm,高为 16cm,现有一根长为 25cm 的吸管任意放入杯中,则吸管露在杯口外的长度最少是( )
A.6cm B.5cm C.9cm D. cm
8.如图,一艘轮船位于灯塔的北偏东方向,与灯塔的距离为海里的处,轮船沿正南方向航行一段时间后,到达位于灯塔的南偏东方向上的处,则此时轮船所在位置处与灯塔之间的距离为( )
A.60 海里 B.45海里 C.20海里 D.30海里
9.如图,一架2.5米长的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为0.7米,如果梯子的顶端下滑0.4米,则梯足将向外移( )
A.0.6米 B.0.7米 C.0.8米 D.0.9米
二.填空题
10.如图,一株荷叶高出水面1m,一阵风吹过来,荷叶被风吹的贴着水面,这时它偏离原来位置有3m远,则荷叶原来的高度是 .
11.已知一个三角形工件尺寸(单位:dm)如图所示,则高h是 dm,它的面积是 dm2.
12.如图,,,,一机器人在点B处看见一个小球从点A出发沿着方向匀速滚向点,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球,如果小球滚动的速度与机器人行走的速度相等,则机器人行走的路程BC为__________.
13.一艘轮船在小岛的北偏东方向距小岛海里的处,沿正西方向航行小时后到达小岛的北偏西的处,则该船行驶的速度为_____海里/小时.
14.如图,有一个三级台阶,它的每一级的长, 宽和高分别是,,,点和点是这个台阶两个相对的端点,点有一只蚂蚁,想到点去吃可口的食物,则蚂蚁沿着台阶表面爬到点的最短路程是____.
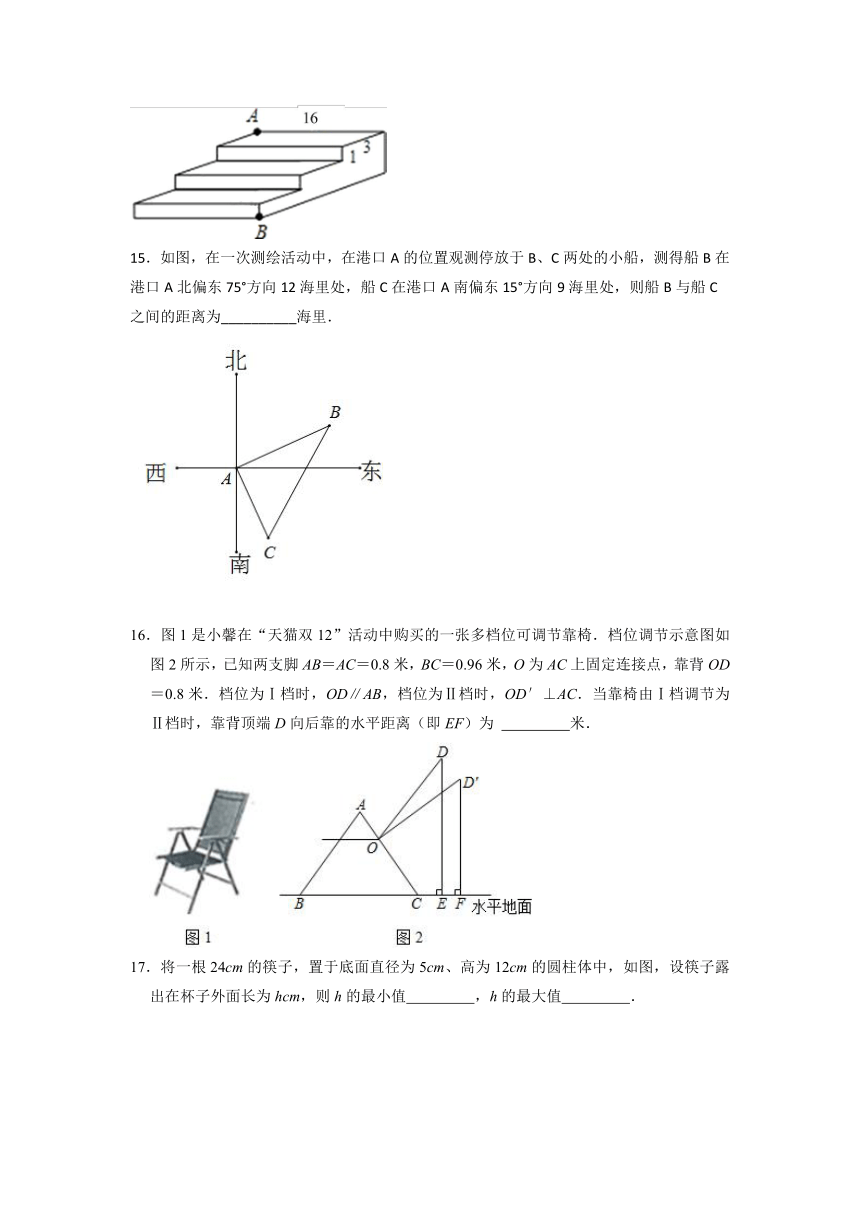
15.如图,在一次测绘活动中,在港口A的位置观测停放于B、C两处的小船,测得船B在港口A北偏东75°方向12海里处,船C在港口A南偏东15°方向9海里处,则船B与船C之间的距离为__________海里.
16.图1是小馨在“天猫双12”活动中购买的一张多档位可调节靠椅.档位调节示意图如图2所示,已知两支脚AB=AC=0.8米,BC=0.96米,O为AC上固定连接点,靠背OD=0.8米.档位为Ⅰ档时,OD∥AB,档位为Ⅱ档时,OD′⊥AC.当靠椅由Ⅰ档调节为Ⅱ档时,靠背顶端D向后靠的水平距离(即EF)为 米.
17.将一根24cm的筷子,置于底面直径为5cm、高为12cm的圆柱体中,如图,设筷子露出在杯子外面长为hcm,则h的最小值 ,h的最大值 .
三.解答题
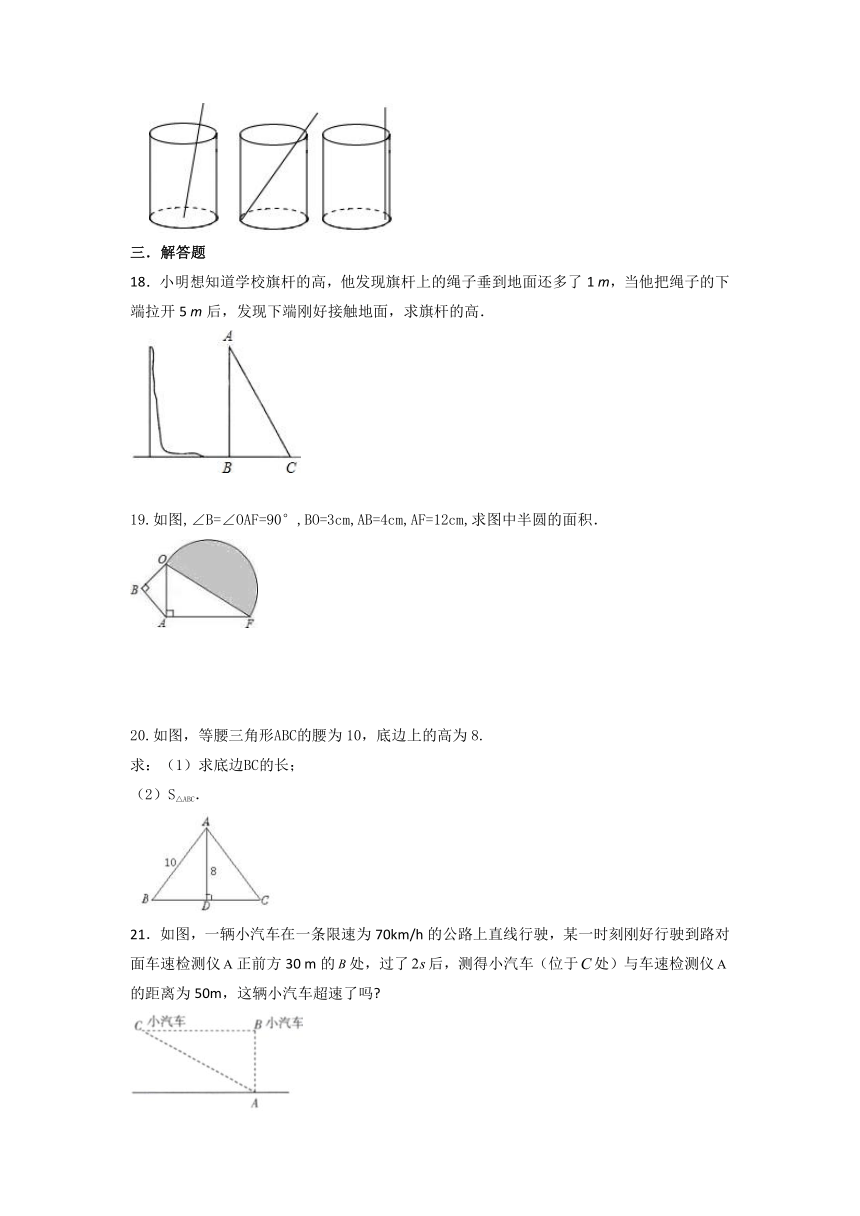
18.小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多了1 m,当他把绳子的下端拉开5 m后,发现下端刚好接触地面,求旗杆的高.
19.如图,∠B=∠OAF=90°,BO=3cm,AB=4cm,AF=12cm,求图中半圆的面积.
20.如图,等腰三角形ABC的腰为10,底边上的高为8.
求:(1)求底边BC的长;
(2)S△ABC.
21.如图,一辆小汽车在一条限速为70km/h的公路上直线行驶,某一时刻刚好行驶到路对面车速检测仪正前方30 m的处,过了后,测得小汽车(位于处)与车速检测仪的距离为50m,这辆小汽车超速了吗
22.如图1,A村和B村在一条大河CD的同侧,它们到河岸的距离AC、BD分别为1千米和4千米,又知道CD的长为4千米.
(1)现要在河岸CD上建一水厂向两村输送自来水.有两种方案备选
方案1:水厂建在C点,修自来水管道到A村,再到B村(即AC+AB).(如图2)
方案2:作A点关于直线CD的对称点A',连接A'B交CD于M点,水厂建在M点处,分别向两村修管道AM和BM.(即AM+BM)(如图3)
从节约建设资金方面考虑,将选择管道总长度较短的方案进行施工,请利用已有条件分别进行计算,判断哪种方案更合适.
(2)有一艘快艇Q从这条河中驶过,当快艇Q在CD中间,DQ为多少时?△ABQ为等腰三角形?
参考答案
一.选择题(共9小题,满分36分)
BCBDD BBD C
二.填空题(共8小题,满分32分)
10.5m.
11.12.
12.5m
13.
14.20
15.
16.解:过A作AG⊥BC于点G,过O作OH⊥BC于H,作OM⊥D'F于点M,交DE于点N,如图所示,
则OM=HE,ON=HE,
∵AB=AC=0.8米,BC=0.96米,
∴BG=CG=BC=0.48米,
∴AG=(米),
∵AB∥OD,BC∥OM,
∴∠ABG=∠DON,
在△ABG和△DON中,
,
∴△ABG≌△DON(AAS),
∴BG=ON=HE=0.48米,
∵OD'⊥AC.
∴∠D'OM+∠MOC=90°,
∵OM∥BC,
∴∠MOC=∠ACG,
∵∠ACG+∠CAG=90°,
∴∠CAG=∠D'OM,
在△ACG和△OD'M中,
,
∴△ACG≌△OD'M(AAS),
∴AG=OM=HF=0.64米,
∴EF=HF﹣HE=0.64﹣0.48=0.16(米),
故答案为:0.16.
17.解:当筷子与杯底垂直时h最大,h最大=24﹣12=12(cm).
当筷子与杯底及杯高构成直角三角形时h最小,
此时,在杯子内部分==13(cm),
故h=24﹣13=11(cm).
故h的取值范围是11≤h≤12.
故答案为:11cm;12cm.
三.解答题(共7小题,满分52分)
18.旗杆的高度为12米
【解析】解:设旗杆的高度为x米,则绳子的长度为(x+1)米,
根据勾股定理可得:x2+52=(x+1)2,
解得,x=12.
答:旗杆的高度为12米.
19.解:如图,∵在直角△ABO中,∠B=90°,BO=3cm,AB=4cm,
∴AO==5cm.
则在直角△AFO中,由勾股定理得到:FO==13cm,
∴图中半圆的面积=π×()2=π×=(cm2).
答:图中半圆的面积是cm2.
20.解:(1)在等腰三角形ABC中,
∵AD⊥BC于D,
∴BD=DC=0.5BC.
∴在Rt△ABD中,由勾股定理可得
AD2+BD2=AB2 , BD2=100-64=36.
∴BD=6
∴BC=BD×2=12.
21.这辆小汽车超速了.
【解析】在Rt△ABC中,AC=30m,AB=50m;
据勾股定理可得:
BC==40(m)
∴小汽车的速度为v==20(m/s)=20×3.6(km/h)=72(km/h);
∵72(km/h)>70(km/h);
∴这辆小汽车超速行驶.
答:这辆小汽车超速了.
22.解:(1)方案1:AC+AB=1+5=6,
方案2:AM+BM=A′B==,
∵6<,
∴方案1更合适;
(2)如图,①AQ1=AB=5或AQ4=AB=5时,
CQ1=CQ4==2,
∴QG=2+2(舍去)或2﹣2(舍去);
②AB=BQ2=5或AB=BQ5=5时,
DQ==3,
∴QG=3+2=5或3﹣2=1(舍去),
③G为CD中点时,当AQ3=BQ3时,
(GQ3+2)2+12=(2﹣GQ3)2+42,
解得:GQ3=,
DQ=.
故当DQ=3或时,△ABQ为等腰三角形.
一.选择题
1.如图,一块三角形木板,测得AB=13,BC=5,AC=12,则三角形木板ABC的面积为( )
A.60 B.30 C.65 D.不能确定
2.如图,在一个高为3米,长为5米的楼梯表面铺地毯,则地毯长度为( )米
A.4米 B.5米 C.7米 D.8米
3.人在平地上以1.5米/秒的速度向东走了80秒,接着以2米/秒的速度向南走了45秒,这时他离开出发点( )
A.180米 B.150米 C.120米 D.100米
4.如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M表示的实数为( )
A.5 B. C. D.
5.国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口A处出发先往东走8km,又往北走2km,遇到障碍后又往西走3km,再向北走到6km处往东拐,仅走了1km,就找到了宝藏,则门口A到藏宝点B的直线距离是( )
A.20km B.14km C.11km D.10km
6.小明同学先向北行进千米,然后向东进千米,再向北行进千米,最后又向东行进一定距离,此时小明离出发点的距离是千米,小明最后向东行进了( )
A.3千米 B.4千米
C.5千米 D.6千米
7.如图是一圆柱玻璃杯,从内部测得底面半径为 6cm,高为 16cm,现有一根长为 25cm 的吸管任意放入杯中,则吸管露在杯口外的长度最少是( )
A.6cm B.5cm C.9cm D. cm
8.如图,一艘轮船位于灯塔的北偏东方向,与灯塔的距离为海里的处,轮船沿正南方向航行一段时间后,到达位于灯塔的南偏东方向上的处,则此时轮船所在位置处与灯塔之间的距离为( )
A.60 海里 B.45海里 C.20海里 D.30海里
9.如图,一架2.5米长的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为0.7米,如果梯子的顶端下滑0.4米,则梯足将向外移( )
A.0.6米 B.0.7米 C.0.8米 D.0.9米
二.填空题
10.如图,一株荷叶高出水面1m,一阵风吹过来,荷叶被风吹的贴着水面,这时它偏离原来位置有3m远,则荷叶原来的高度是 .
11.已知一个三角形工件尺寸(单位:dm)如图所示,则高h是 dm,它的面积是 dm2.
12.如图,,,,一机器人在点B处看见一个小球从点A出发沿着方向匀速滚向点,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球,如果小球滚动的速度与机器人行走的速度相等,则机器人行走的路程BC为__________.
13.一艘轮船在小岛的北偏东方向距小岛海里的处,沿正西方向航行小时后到达小岛的北偏西的处,则该船行驶的速度为_____海里/小时.
14.如图,有一个三级台阶,它的每一级的长, 宽和高分别是,,,点和点是这个台阶两个相对的端点,点有一只蚂蚁,想到点去吃可口的食物,则蚂蚁沿着台阶表面爬到点的最短路程是____.
15.如图,在一次测绘活动中,在港口A的位置观测停放于B、C两处的小船,测得船B在港口A北偏东75°方向12海里处,船C在港口A南偏东15°方向9海里处,则船B与船C之间的距离为__________海里.
16.图1是小馨在“天猫双12”活动中购买的一张多档位可调节靠椅.档位调节示意图如图2所示,已知两支脚AB=AC=0.8米,BC=0.96米,O为AC上固定连接点,靠背OD=0.8米.档位为Ⅰ档时,OD∥AB,档位为Ⅱ档时,OD′⊥AC.当靠椅由Ⅰ档调节为Ⅱ档时,靠背顶端D向后靠的水平距离(即EF)为 米.
17.将一根24cm的筷子,置于底面直径为5cm、高为12cm的圆柱体中,如图,设筷子露出在杯子外面长为hcm,则h的最小值 ,h的最大值 .
三.解答题
18.小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多了1 m,当他把绳子的下端拉开5 m后,发现下端刚好接触地面,求旗杆的高.
19.如图,∠B=∠OAF=90°,BO=3cm,AB=4cm,AF=12cm,求图中半圆的面积.
20.如图,等腰三角形ABC的腰为10,底边上的高为8.
求:(1)求底边BC的长;
(2)S△ABC.
21.如图,一辆小汽车在一条限速为70km/h的公路上直线行驶,某一时刻刚好行驶到路对面车速检测仪正前方30 m的处,过了后,测得小汽车(位于处)与车速检测仪的距离为50m,这辆小汽车超速了吗
22.如图1,A村和B村在一条大河CD的同侧,它们到河岸的距离AC、BD分别为1千米和4千米,又知道CD的长为4千米.
(1)现要在河岸CD上建一水厂向两村输送自来水.有两种方案备选
方案1:水厂建在C点,修自来水管道到A村,再到B村(即AC+AB).(如图2)
方案2:作A点关于直线CD的对称点A',连接A'B交CD于M点,水厂建在M点处,分别向两村修管道AM和BM.(即AM+BM)(如图3)
从节约建设资金方面考虑,将选择管道总长度较短的方案进行施工,请利用已有条件分别进行计算,判断哪种方案更合适.
(2)有一艘快艇Q从这条河中驶过,当快艇Q在CD中间,DQ为多少时?△ABQ为等腰三角形?
参考答案
一.选择题(共9小题,满分36分)
BCBDD BBD C
二.填空题(共8小题,满分32分)
10.5m.
11.12.
12.5m
13.
14.20
15.
16.解:过A作AG⊥BC于点G,过O作OH⊥BC于H,作OM⊥D'F于点M,交DE于点N,如图所示,
则OM=HE,ON=HE,
∵AB=AC=0.8米,BC=0.96米,
∴BG=CG=BC=0.48米,
∴AG=(米),
∵AB∥OD,BC∥OM,
∴∠ABG=∠DON,
在△ABG和△DON中,
,
∴△ABG≌△DON(AAS),
∴BG=ON=HE=0.48米,
∵OD'⊥AC.
∴∠D'OM+∠MOC=90°,
∵OM∥BC,
∴∠MOC=∠ACG,
∵∠ACG+∠CAG=90°,
∴∠CAG=∠D'OM,
在△ACG和△OD'M中,
,
∴△ACG≌△OD'M(AAS),
∴AG=OM=HF=0.64米,
∴EF=HF﹣HE=0.64﹣0.48=0.16(米),
故答案为:0.16.
17.解:当筷子与杯底垂直时h最大,h最大=24﹣12=12(cm).
当筷子与杯底及杯高构成直角三角形时h最小,
此时,在杯子内部分==13(cm),
故h=24﹣13=11(cm).
故h的取值范围是11≤h≤12.
故答案为:11cm;12cm.
三.解答题(共7小题,满分52分)
18.旗杆的高度为12米
【解析】解:设旗杆的高度为x米,则绳子的长度为(x+1)米,
根据勾股定理可得:x2+52=(x+1)2,
解得,x=12.
答:旗杆的高度为12米.
19.解:如图,∵在直角△ABO中,∠B=90°,BO=3cm,AB=4cm,
∴AO==5cm.
则在直角△AFO中,由勾股定理得到:FO==13cm,
∴图中半圆的面积=π×()2=π×=(cm2).
答:图中半圆的面积是cm2.
20.解:(1)在等腰三角形ABC中,
∵AD⊥BC于D,
∴BD=DC=0.5BC.
∴在Rt△ABD中,由勾股定理可得
AD2+BD2=AB2 , BD2=100-64=36.
∴BD=6
∴BC=BD×2=12.
21.这辆小汽车超速了.
【解析】在Rt△ABC中,AC=30m,AB=50m;
据勾股定理可得:
BC==40(m)
∴小汽车的速度为v==20(m/s)=20×3.6(km/h)=72(km/h);
∵72(km/h)>70(km/h);
∴这辆小汽车超速行驶.
答:这辆小汽车超速了.
22.解:(1)方案1:AC+AB=1+5=6,
方案2:AM+BM=A′B==,
∵6<,
∴方案1更合适;
(2)如图,①AQ1=AB=5或AQ4=AB=5时,
CQ1=CQ4==2,
∴QG=2+2(舍去)或2﹣2(舍去);
②AB=BQ2=5或AB=BQ5=5时,
DQ==3,
∴QG=3+2=5或3﹣2=1(舍去),
③G为CD中点时,当AQ3=BQ3时,
(GQ3+2)2+12=(2﹣GQ3)2+42,
解得:GQ3=,
DQ=.
故当DQ=3或时,△ABQ为等腰三角形.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
