2021-2022学年沪科版九年级数学上册 第23章 解直角三角形 同步测试卷 (word版含答案)
文档属性
| 名称 | 2021-2022学年沪科版九年级数学上册 第23章 解直角三角形 同步测试卷 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 198.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 19:08:47 | ||
图片预览




文档简介
第23章解直角三角形同步测试卷 2021-2022学年度沪科版九年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
如图,在RtABC中,C=,AB=5,BC=3,则 B 的值为( )
A. B.
C. D.
在直角三角形中,根据下列条件,不能解三角形的是( )
A. 已知一直角边和一锐角 B. 已知斜边和一锐角
C. 已知两边 D. 已知两角
在RtABC中,C=,BC=1,AC=,那么B的度数是( )
A. B. C. D.
在RtABC中,C=,若AB=4,=,则斜边上的高等于( )
A. B. C. D.
已知锐角的正切值为,那么下列结论中正确的是( )
A. B. C. D.
在平面直角坐标系中,点A的坐标为(0,3),点B在x轴上,且OAB=,则点B的坐标为( )
A. B.
C. 或 D. 或
等腰三角形一腰上的高与腰长之比是1:2,则等腰三角形顶角的度数为( )
A. B. C. 或 D. 或
如图是边长为1的小正方形组成的网格图,其中点A,B,C均为格点,则为( )
A. B.
C. D.
在ABC中,ACB=,A=,D是AB的中点,则BCD+ACD等于( )
A. B. C. D.
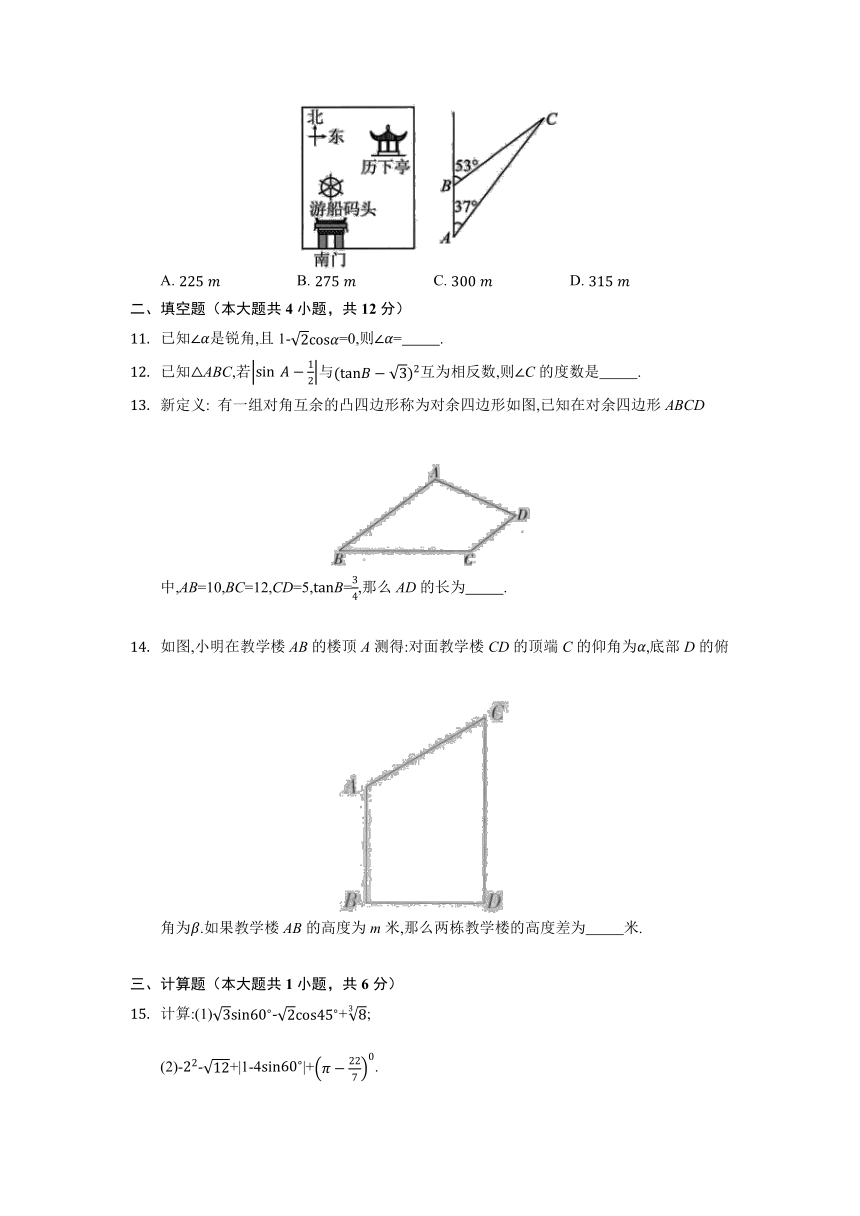
如图,某数学社团开展实践性研究,在大明湖南门A处测得历下亭C在北偏东方向,继续向北走105 m后到达游船码头B处,测得历下亭C在游船码头B的北偏东方向.请计算一下南门A与历下亭C之间的距离约为(参考数据:,)( )
A. B. C. D.
二、填空题(本大题共4小题,共12分)
已知是锐角,且1-=0,则= .
已知ABC,若与互为相反数,则C的度数是 .
新定义: 有一组对角互余的凸四边形称为对余四边形如图,已知在对余四边形ABCD中,AB=10,BC=12,CD=5,B=,那么AD的长为 .
如图,小明在教学楼AB的楼顶A测得:对面教学楼CD的顶端C的仰角为,底部D的俯角为.如果教学楼AB的高度为m米,那么两栋教学楼的高度差为 米.
三、计算题(本大题共1小题,共6分)
计算:(1)-+;
(2)--+|1-4|+.
四、解答题(本大题共7小题,共72分)
在RtABC中,C为直角,A,B,C所对的边分别为a,b,c,根据下列条件解直角三角形ABC.
(1)已知c=20,A=;
(2)已知a=,b=.
如图,在ABC中,AB=AC=10,B=.
(1)求BC的长;
(2)求A的值.
某公司举办气球表演来庆祝开业,如图,小敏、小亮从A,B两地观测空中C处一个气球,分别测得仰角为和,A、B两地相距10m.当气球沿与BA平行的直线飘移100秒后到达D处时,在A处测得气球的仰角为.
(1)求气球的高度;
(2)求气球飘移的平均速度.
(结果精确到0.01m.参考数据:0.60,0.80,0.75,1.73)
某数学小组开展了一次测量小山高度的活动,如图,该数学小组从地面A处出发,沿坡角为的山坡AB直线上行350米到达B处,再沿着坡角为的山坡BC直线上行600米到达C处.求小山的高度CD及该数学小组行进的水平距离AD(结果精确到1米).(参考数据:0.37,0.93,0.80,0.60)
如图,台风中心位于点O处,并沿北偏东方向(OC方向)以40千米/时的速度匀速移动,在距离台风中心50千米的区域内会受到台风的影响,在点O的正东方向,距离60千米的地方有一城市A.
(1)A市是否会受到此台风的影响 为什么
(2)在点O的北偏东方向上,距离80千米的地方还有一城市B,则B市是否会受到此台风的影响 若受到影响,请求出受到影响的时间;若不受影响,请说明理由.
如图,垂直于水平面的5G信号塔AB建在垂直于地面的悬崖的B点处(点A、B、C在同一直线上).某测量员从悬崖底C点出发沿水平方向前行60米到达D点,再沿斜坡DE方向前行65米到达E点(点A、B、C、D、E在同一平面内),在点E处测得5G信号塔顶端A的仰角为,悬崖BC的高为92米,斜坡DE的坡度i=1:2.4.
(1)求斜坡DE的高;
(2)求信号塔AB的高度.
(参考数据:0.60,0.80,0.75)
如图,山坡上有一棵与地面EF垂直的大树AB,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部B恰好落在山坡上的点D处,已知山坡的坡角AEF=,量得BAC=,大树被折断部分和坡面所成的角ADC=,AD=4m.
(1)求CAE的度数;
(2)求这棵大树折断前的高度.(结果保留整数,参考数据:1.4,1.7,2.4)
参考答案
1.【答案】A
2.【答案】D
3.【答案】D
4.【答案】D
5.【答案】C
6.【答案】C
7.【答案】D
8.【答案】D
9.【答案】A
10.【答案】C
11.【答案】
12.【答案】
13.【答案】9
14.【答案】
15.【答案】解:(1)原式=-+2=-1+2=.
(2)原式=-4-2+|1-4|+1
=-4-2+2-1+1=-4.
16.【答案】解: (1)A=,C为直角,
B=-=.
c=20,B=,
b=c=10.
a===10.
(2)C为直角,a=,b=,
c===2.
B===,
B=.A=-=.
17.【答案】解:(1)如图,过点A作ADBC于点D,
AB=AC=10,BC=2BD,
在RtABD中,ABD=,
AD=ABABD=10=8,
BD===6,
则BC=2BD=12.
(2)如图,过点B作BHAC于H,
=ACBH=CBAD,
BH===,
AH===,
BAC===.
18.【答案】解:(1)如图,过点C作CE直线AB于点E,
在RtACE中,
CAE=,CE=AE0.75AE,
即AE=CE,
在RtBCE中,CBE=,BE=CE,
AB=AE-BE=CE-CE=CE=10米,
CE=30(米).
答:气球的高度约为30米.
(2)如图,过点D作DF直线AB于点F,则四边形DFEC是矩形,
在RtADF中,
DAF=,AF=DF=CE=1017.3(米),
AE=CE=40(米),
CD=EF=40-17.3=22.7(米),
22.71000.23米/秒.
答:气球飘移的平均速度约为0.23米/秒.
19.【答案】解:如图,过B作BECD于E,过B作BHAD于H,则四边形BEDH是矩形,
DE=BH,BE=DH.
在RtBCE中,BC=600米,CBE=,
CE=BC6000.37=222(米),
BE=BC6000.93=558(米),
DH=BE=558(米).
在RtABH中,AB=350米,
BH=AB3500.80=280(米),
AH=AB3500.60=210(米),
CD=CE+DE=CE+BH=222+280=502(米),
AD=AH+DH=210+558=768(米).
答:小山的高度CD为502米,该数学小组行进的水平距离AD为768米.
20.【答案】解:(1)不会.理由:如图,过点A作AEOC于点E.
在RtAOE中,=,
AE=60=60(千米).
60千米>50千米,
A市不会受到此台风的影响.
(2)会.如图,过点B作BFOC于点F.
在RtBOF中,
BOF=-=,=,
BF=80=40(千米).
40千米<50千米,B市会受到台风的影响.
如图,以点B为圆心,50千米为半径作圆交OC于点G,H.
在RtBGF中,BF=40千米,
GF==30(千米).
同理,FH=30千米.
GH=60千米,则6040=1.5(时),
B市受到台风影响的时间为1.5小时.
21.【答案】解:(1)过点E作EMAC于点M,
斜坡DE的坡度i=1:2.4,
设EH=x米,则DH=2.4x米.
在RtDEH中,DE=65米,
+=,即+=,
解得x=25(负值舍去),EH=25米.
答:斜坡DE的高为25米.
(2)由(1)得DH=2.425=60(米),
CH=DH+DC=60+60=120(米).
EMAC,ACCD,EHCD,
四边形EHCM是矩形,
EM=CH=120米,CM=EH=25米.
在RtAEM中,AEM=,
AM=EM1200.75=90(米),
AC=AM+CM=90+25=115(米).
AB=AC-BC=115-92=23(米).
答:信号塔AB的高度约为23米.
22.【答案】解:(1)延长BA交EF于点G,在RtAGE中,
AEF=,GAE=.
又BAC=,CAE=--=.
(2)过点A作AHCD,垂足为H.
在ADH中,ADC=,AD=4m,
DH=ADADC=4=2(m),AH=ADADC=4=2(m).
在RtACD中,C=--=,
CH=AH=2m,
AC===2(m),
AB=AC+CD=2+2+210(m).
答:这棵大树折断前的高度约为10m.
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
如图,在RtABC中,C=,AB=5,BC=3,则 B 的值为( )
A. B.
C. D.
在直角三角形中,根据下列条件,不能解三角形的是( )
A. 已知一直角边和一锐角 B. 已知斜边和一锐角
C. 已知两边 D. 已知两角
在RtABC中,C=,BC=1,AC=,那么B的度数是( )
A. B. C. D.
在RtABC中,C=,若AB=4,=,则斜边上的高等于( )
A. B. C. D.
已知锐角的正切值为,那么下列结论中正确的是( )
A. B. C. D.
在平面直角坐标系中,点A的坐标为(0,3),点B在x轴上,且OAB=,则点B的坐标为( )
A. B.
C. 或 D. 或
等腰三角形一腰上的高与腰长之比是1:2,则等腰三角形顶角的度数为( )
A. B. C. 或 D. 或
如图是边长为1的小正方形组成的网格图,其中点A,B,C均为格点,则为( )
A. B.
C. D.
在ABC中,ACB=,A=,D是AB的中点,则BCD+ACD等于( )
A. B. C. D.
如图,某数学社团开展实践性研究,在大明湖南门A处测得历下亭C在北偏东方向,继续向北走105 m后到达游船码头B处,测得历下亭C在游船码头B的北偏东方向.请计算一下南门A与历下亭C之间的距离约为(参考数据:,)( )
A. B. C. D.
二、填空题(本大题共4小题,共12分)
已知是锐角,且1-=0,则= .
已知ABC,若与互为相反数,则C的度数是 .
新定义: 有一组对角互余的凸四边形称为对余四边形如图,已知在对余四边形ABCD中,AB=10,BC=12,CD=5,B=,那么AD的长为 .
如图,小明在教学楼AB的楼顶A测得:对面教学楼CD的顶端C的仰角为,底部D的俯角为.如果教学楼AB的高度为m米,那么两栋教学楼的高度差为 米.
三、计算题(本大题共1小题,共6分)
计算:(1)-+;
(2)--+|1-4|+.
四、解答题(本大题共7小题,共72分)
在RtABC中,C为直角,A,B,C所对的边分别为a,b,c,根据下列条件解直角三角形ABC.
(1)已知c=20,A=;
(2)已知a=,b=.
如图,在ABC中,AB=AC=10,B=.
(1)求BC的长;
(2)求A的值.
某公司举办气球表演来庆祝开业,如图,小敏、小亮从A,B两地观测空中C处一个气球,分别测得仰角为和,A、B两地相距10m.当气球沿与BA平行的直线飘移100秒后到达D处时,在A处测得气球的仰角为.
(1)求气球的高度;
(2)求气球飘移的平均速度.
(结果精确到0.01m.参考数据:0.60,0.80,0.75,1.73)
某数学小组开展了一次测量小山高度的活动,如图,该数学小组从地面A处出发,沿坡角为的山坡AB直线上行350米到达B处,再沿着坡角为的山坡BC直线上行600米到达C处.求小山的高度CD及该数学小组行进的水平距离AD(结果精确到1米).(参考数据:0.37,0.93,0.80,0.60)
如图,台风中心位于点O处,并沿北偏东方向(OC方向)以40千米/时的速度匀速移动,在距离台风中心50千米的区域内会受到台风的影响,在点O的正东方向,距离60千米的地方有一城市A.
(1)A市是否会受到此台风的影响 为什么
(2)在点O的北偏东方向上,距离80千米的地方还有一城市B,则B市是否会受到此台风的影响 若受到影响,请求出受到影响的时间;若不受影响,请说明理由.
如图,垂直于水平面的5G信号塔AB建在垂直于地面的悬崖的B点处(点A、B、C在同一直线上).某测量员从悬崖底C点出发沿水平方向前行60米到达D点,再沿斜坡DE方向前行65米到达E点(点A、B、C、D、E在同一平面内),在点E处测得5G信号塔顶端A的仰角为,悬崖BC的高为92米,斜坡DE的坡度i=1:2.4.
(1)求斜坡DE的高;
(2)求信号塔AB的高度.
(参考数据:0.60,0.80,0.75)
如图,山坡上有一棵与地面EF垂直的大树AB,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部B恰好落在山坡上的点D处,已知山坡的坡角AEF=,量得BAC=,大树被折断部分和坡面所成的角ADC=,AD=4m.
(1)求CAE的度数;
(2)求这棵大树折断前的高度.(结果保留整数,参考数据:1.4,1.7,2.4)
参考答案
1.【答案】A
2.【答案】D
3.【答案】D
4.【答案】D
5.【答案】C
6.【答案】C
7.【答案】D
8.【答案】D
9.【答案】A
10.【答案】C
11.【答案】
12.【答案】
13.【答案】9
14.【答案】
15.【答案】解:(1)原式=-+2=-1+2=.
(2)原式=-4-2+|1-4|+1
=-4-2+2-1+1=-4.
16.【答案】解: (1)A=,C为直角,
B=-=.
c=20,B=,
b=c=10.
a===10.
(2)C为直角,a=,b=,
c===2.
B===,
B=.A=-=.
17.【答案】解:(1)如图,过点A作ADBC于点D,
AB=AC=10,BC=2BD,
在RtABD中,ABD=,
AD=ABABD=10=8,
BD===6,
则BC=2BD=12.
(2)如图,过点B作BHAC于H,
=ACBH=CBAD,
BH===,
AH===,
BAC===.
18.【答案】解:(1)如图,过点C作CE直线AB于点E,
在RtACE中,
CAE=,CE=AE0.75AE,
即AE=CE,
在RtBCE中,CBE=,BE=CE,
AB=AE-BE=CE-CE=CE=10米,
CE=30(米).
答:气球的高度约为30米.
(2)如图,过点D作DF直线AB于点F,则四边形DFEC是矩形,
在RtADF中,
DAF=,AF=DF=CE=1017.3(米),
AE=CE=40(米),
CD=EF=40-17.3=22.7(米),
22.71000.23米/秒.
答:气球飘移的平均速度约为0.23米/秒.
19.【答案】解:如图,过B作BECD于E,过B作BHAD于H,则四边形BEDH是矩形,
DE=BH,BE=DH.
在RtBCE中,BC=600米,CBE=,
CE=BC6000.37=222(米),
BE=BC6000.93=558(米),
DH=BE=558(米).
在RtABH中,AB=350米,
BH=AB3500.80=280(米),
AH=AB3500.60=210(米),
CD=CE+DE=CE+BH=222+280=502(米),
AD=AH+DH=210+558=768(米).
答:小山的高度CD为502米,该数学小组行进的水平距离AD为768米.
20.【答案】解:(1)不会.理由:如图,过点A作AEOC于点E.
在RtAOE中,=,
AE=60=60(千米).
60千米>50千米,
A市不会受到此台风的影响.
(2)会.如图,过点B作BFOC于点F.
在RtBOF中,
BOF=-=,=,
BF=80=40(千米).
40千米<50千米,B市会受到台风的影响.
如图,以点B为圆心,50千米为半径作圆交OC于点G,H.
在RtBGF中,BF=40千米,
GF==30(千米).
同理,FH=30千米.
GH=60千米,则6040=1.5(时),
B市受到台风影响的时间为1.5小时.
21.【答案】解:(1)过点E作EMAC于点M,
斜坡DE的坡度i=1:2.4,
设EH=x米,则DH=2.4x米.
在RtDEH中,DE=65米,
+=,即+=,
解得x=25(负值舍去),EH=25米.
答:斜坡DE的高为25米.
(2)由(1)得DH=2.425=60(米),
CH=DH+DC=60+60=120(米).
EMAC,ACCD,EHCD,
四边形EHCM是矩形,
EM=CH=120米,CM=EH=25米.
在RtAEM中,AEM=,
AM=EM1200.75=90(米),
AC=AM+CM=90+25=115(米).
AB=AC-BC=115-92=23(米).
答:信号塔AB的高度约为23米.
22.【答案】解:(1)延长BA交EF于点G,在RtAGE中,
AEF=,GAE=.
又BAC=,CAE=--=.
(2)过点A作AHCD,垂足为H.
在ADH中,ADC=,AD=4m,
DH=ADADC=4=2(m),AH=ADADC=4=2(m).
在RtACD中,C=--=,
CH=AH=2m,
AC===2(m),
AB=AC+CD=2+2+210(m).
答:这棵大树折断前的高度约为10m.
第1页,共1页
