7.1 行星的运动练习(Word版含解析)
文档属性
| 名称 | 7.1 行星的运动练习(Word版含解析) | 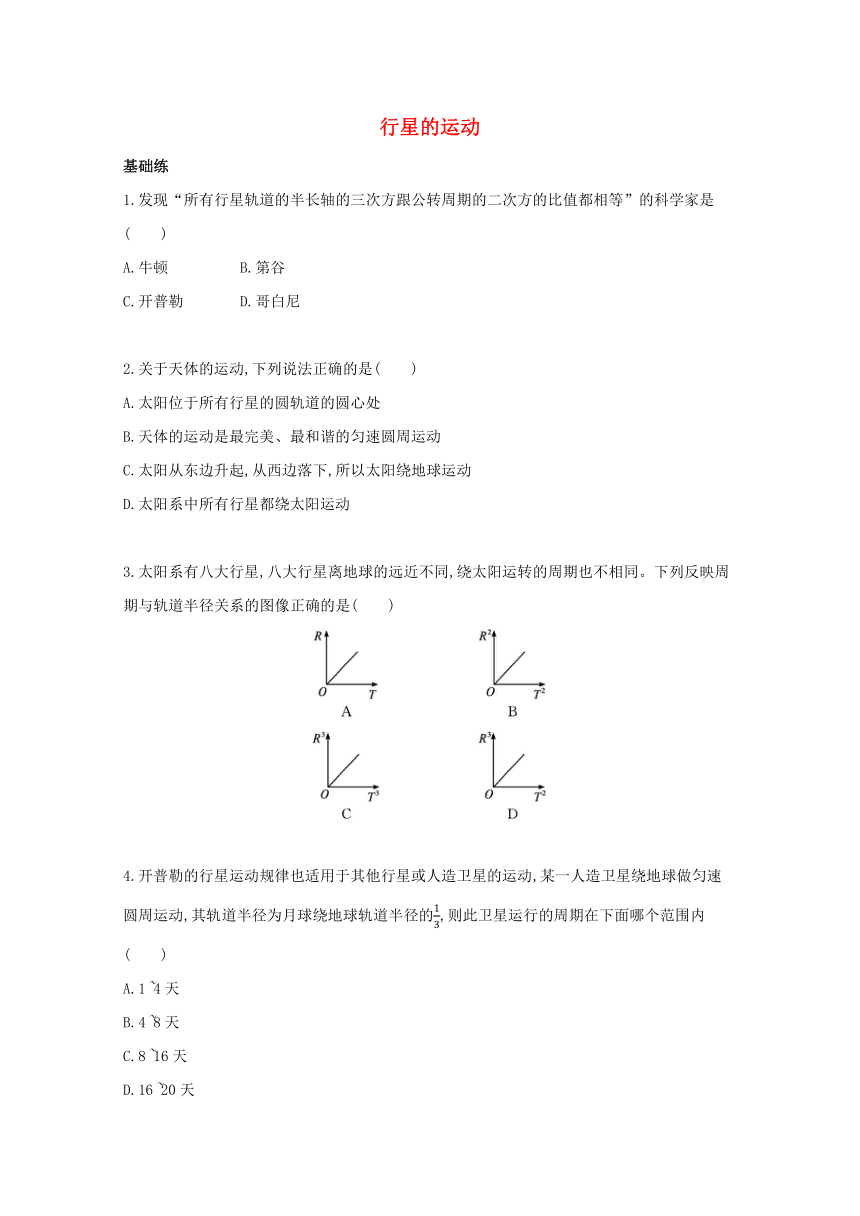 | |
| 格式 | docx | ||
| 文件大小 | 182.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-11-23 15:41:19 | ||
图片预览




文档简介
行星的运动
基础练
1.发现“所有行星轨道的半长轴的三次方跟公转周期的二次方的比值都相等”的科学家是( )
A.牛顿 B.第谷
C.开普勒 D.哥白尼
2.关于天体的运动,下列说法正确的是( )
A.太阳位于所有行星的圆轨道的圆心处
B.天体的运动是最完美、最和谐的匀速圆周运动
C.太阳从东边升起,从西边落下,所以太阳绕地球运动
D.太阳系中所有行星都绕太阳运动
3.太阳系有八大行星,八大行星离地球的远近不同,绕太阳运转的周期也不相同。下列反映周期与轨道半径关系的图像正确的是( )
4.开普勒的行星运动规律也适用于其他行星或人造卫星的运动,某一人造卫星绕地球做匀速圆周运动,其轨道半径为月球绕地球轨道半径的,则此卫星运行的周期在下面哪个范围内( )
A.1~4天
B.4~8天
C.8~16天
D.16~20天
5.地球公转轨道的半径在天文学上常用来作为长度单位,叫作天文单位,用来量度太阳系内行星与太阳的距离。已知火星公转的周期是1.84年,根据开普勒第三定律,火星公转轨道半径是多少天文单位 (将地球和火星绕太阳公转的轨道近似成圆形轨道。)
6.土星直径为119 300 km,是太阳系中第二大行星,其自转周期为10 h 39 min,公转周期为29.4年,距离太阳1.432×109 km。土星最引人注目的是绕着其赤道的巨大光环。在地球上人们只需要一架小型望远镜就能清楚地看到光环,环的外沿直径约为274 000 km。请由上面提供的信息,估算地球距太阳有多远。(保留3位有效数字)
提升练
1.某行星绕太阳沿椭圆轨道运行,如图所示,在这颗行星的轨道上有a、b、c、d四个对称点,若行星运动周期为T,则该行星( )
A.从a到b的运动时间等于从c到d的运动时间
B.从d经a到b的运动时间等于从b经c到d的运动时间
C.从a到b的时间tab>
D.从c到d的时间tcd>
2.如图所示,某行星沿椭圆轨道运行,远日点离太阳的距离为a,近日点离太阳的距离为b,过远日点时行星的速率为va,则过近日点时的速率为( )
A.vb=va B.vb=va
C.vb=va D.vb=va
3.对开普勒第一定律的理解,下列说法正确的是( )
A.在行星绕太阳运动一周的时间内,它离太阳的距离是不变的
B.在行星绕太阳运动一周的时间内,它离太阳的距离是变化的
C.太阳不一定在所有行星运动椭圆轨迹的焦点上
D.某个行星绕太阳运动的轨道一定不在一个固定的平面内
4.2016年8月16日凌晨,被命名为墨子号的中国首颗量子科学实验卫星开启星际之旅,其运行轨道为如图所示的椭圆轨道,地球E位于椭圆的一个焦点上。轨道上标记了墨子卫星经过相等时间间隔(Δt=,T为轨道周期)的位置。下列说法正确的是( )
A.面积S1>S2
B.卫星在轨道A点的速度小于在B点的速度
C.T2=Ca3,其中C为常数,a为椭圆半长轴
D.T2=C'b3,其中C'为常数,b为椭圆半短轴
5.月球环绕地球运动的轨道半径约为地球半径的60倍,运行周期约为27天。应用开普勒定律计算:在赤道平面内离地多高时,人造地球卫星随地球一起转动,就像停留在天空中一样。结果保留三位有效数字,取R地=6 400 km。
6.地球的公转轨道接近圆,但彗星的运动轨道则是一个非常扁的椭圆,天文学家哈雷曾经在1682年跟踪过一颗彗星,他算出这颗彗星轨道的半长轴约等于地球轨道半径的18倍,并预言这颗彗星将每隔一定时间就会出现,哈雷的预言得到证实,该彗星被命名为哈雷彗星。哈雷彗星最近出现的时间是1986年,请你根据开普勒第三定律即=k,其中T为行星绕太阳公转的周期,r为轨道的半长轴估算,如果忽略其他影响,它下次飞近地球大约在哪一年
参考答案:
基础练
1.发现“所有行星轨道的半长轴的三次方跟公转周期的二次方的比值都相等”的科学家是( )
A.牛顿 B.第谷
C.开普勒 D.哥白尼
解析:所有行星轨道的半长轴的三次方跟公转周期的二次方的比值都相等,也就是开普勒第三定律,是开普勒发现的。
答案:C
2.关于天体的运动,下列说法正确的是( )
A.太阳位于所有行星的圆轨道的圆心处
B.天体的运动是最完美、最和谐的匀速圆周运动
C.太阳从东边升起,从西边落下,所以太阳绕地球运动
D.太阳系中所有行星都绕太阳运动
解析:天体的运动轨道都是椭圆,而不是圆,故A、B错误。太阳从东边升起,又从西边落下,是地球自转的结果,故C错误。
答案:D
3.太阳系有八大行星,八大行星离地球的远近不同,绕太阳运转的周期也不相同。下列反映周期与轨道半径关系的图像正确的是( )
解析:由开普勒第三定律知=k,所以R3=kT2,D正确。
答案:D
4.开普勒的行星运动规律也适用于其他行星或人造卫星的运动,某一人造卫星绕地球做匀速圆周运动,其轨道半径为月球绕地球轨道半径的,则此卫星运行的周期在下面哪个范围内( )
A.1~4天
B.4~8天
C.8~16天
D.16~20天
解析:由开普勒第三定律=k,得,所以T星=T月=×27天=5.2天,B正确。
答案:B
5.地球公转轨道的半径在天文学上常用来作为长度单位,叫作天文单位,用来量度太阳系内行星与太阳的距离。已知火星公转的周期是1.84年,根据开普勒第三定律,火星公转轨道半径是多少天文单位 (将地球和火星绕太阳公转的轨道近似成圆形轨道。)
解析:设地球和火星的轨道半径分别为r1、r2,公转周期分别为T1、T2。
根据开普勒第三定律得,
得r2=·r1=1.5天文单位。
答案:1.5
6.土星直径为119 300 km,是太阳系中第二大行星,其自转周期为10 h 39 min,公转周期为29.4年,距离太阳1.432×109 km。土星最引人注目的是绕着其赤道的巨大光环。在地球上人们只需要一架小型望远镜就能清楚地看到光环,环的外沿直径约为274 000 km。请由上面提供的信息,估算地球距太阳有多远。(保留3位有效数字)
解析:根据开普勒第三定律有=k,k只与太阳质量有关。则,其中T为公转周期,R为行星到太阳的距离。代入数值,解得R地=1.50×1011m=1.50×108km。
答案:约1.50×108 km
提升练
1.某行星绕太阳沿椭圆轨道运行,如图所示,在这颗行星的轨道上有a、b、c、d四个对称点,若行星运动周期为T,则该行星( )
A.从a到b的运动时间等于从c到d的运动时间
B.从d经a到b的运动时间等于从b经c到d的运动时间
C.从a到b的时间tab>
D.从c到d的时间tcd>
解析:根据开普勒第二定律知行星在近日点速度最大,远日点速度最小。行星由a到b运动的平均速度大于由c到d运动的平均速度,而弧长ab等于弧长cd,故A错误;同理可知B错误;在整个椭圆轨道上tab=tda<,tcd=tbc>,故C错误,D正确。
答案:D
2.如图所示,某行星沿椭圆轨道运行,远日点离太阳的距离为a,近日点离太阳的距离为b,过远日点时行星的速率为va,则过近日点时的速率为( )
A.vb=va B.vb=va
C.vb=va D.vb=va
解析:若行星从轨道的A点经足够短的时间t运动到A'点,则与太阳的连线扫过的面积可看作扇形,其面积SA=;若行星从轨道的B点也经时间t运动到B'点,则与太阳的连线扫过的面积SB=;根据开普勒第二定律得,即vb=va,C正确。
答案:C
3.对开普勒第一定律的理解,下列说法正确的是( )
A.在行星绕太阳运动一周的时间内,它离太阳的距离是不变的
B.在行星绕太阳运动一周的时间内,它离太阳的距离是变化的
C.太阳不一定在所有行星运动椭圆轨迹的焦点上
D.某个行星绕太阳运动的轨道一定不在一个固定的平面内
解析:根据开普勒第一定律的内容可以判定,行星绕太阳运动的轨道是椭圆,有时远离太阳,行星有时靠近太阳,所以它离太阳的距离是变化的,A错误,B正确;太阳一定在所有行星运动的椭圆轨迹的焦点上,C错误;行星绕太阳运动的轨道一定在一个固定的平面内,D错误。
答案:B
4.2016年8月16日凌晨,被命名为墨子号的中国首颗量子科学实验卫星开启星际之旅,其运行轨道为如图所示的椭圆轨道,地球E位于椭圆的一个焦点上。轨道上标记了墨子卫星经过相等时间间隔(Δt=,T为轨道周期)的位置。下列说法正确的是( )
A.面积S1>S2
B.卫星在轨道A点的速度小于在B点的速度
C.T2=Ca3,其中C为常数,a为椭圆半长轴
D.T2=C'b3,其中C'为常数,b为椭圆半短轴
解析:根据开普勒第二定律可知,卫星与地球的连线在相同时间内扫过的面积相等,故面积S1=S2,选项A错误;根据开普勒第二定律可知,卫星在轨道A点的速度大于在B点的速度,选项B错误;根据开普勒第三定律可知=C,故选项C正确,D错误。
答案:C
5.月球环绕地球运动的轨道半径约为地球半径的60倍,运行周期约为27天。应用开普勒定律计算:在赤道平面内离地多高时,人造地球卫星随地球一起转动,就像停留在天空中一样。结果保留三位有效数字,取R地=6 400 km。
解析:月球和人造地球卫星都环绕地球运动,故可用开普勒第三定律求解。当人造地球卫星相对地球不动时,人造地球卫星的周期与地球自转周期相同。
设人造地球卫星轨道半径为R、周期为T。
根据题意知月球轨道半径为60R地,
周期为T0=27天,则有
,整理得
R=×60R地=×60R地=6.67R地。
卫星离地高度h=R-R地=5.67R地=5.67×6400km=3.63×104km。
答案:3.63×104 km
6.地球的公转轨道接近圆,但彗星的运动轨道则是一个非常扁的椭圆,天文学家哈雷曾经在1682年跟踪过一颗彗星,他算出这颗彗星轨道的半长轴约等于地球轨道半径的18倍,并预言这颗彗星将每隔一定时间就会出现,哈雷的预言得到证实,该彗星被命名为哈雷彗星。哈雷彗星最近出现的时间是1986年,请你根据开普勒第三定律即=k,其中T为行星绕太阳公转的周期,r为轨道的半长轴估算,如果忽略其他影响,它下次飞近地球大约在哪一年
解析:=k,其中T为行星绕太阳公转的周期,r为轨道的半长轴,k是对太阳系中的任何行星都适用的常量。可以根据已知条件列方程求解。
将地球的公转轨道近似成圆形轨道,其周期为T1,半径为r1;哈雷彗星的周期为T2,轨道半长轴为r2,则根据开普勒第三定律有
因为r2=18r1,地球公转周期为1年,所以可知哈雷彗星的周期为
T2=×T1=76.4年
所以它下次飞近地球大约是在2062年。
答案:2062年
基础练
1.发现“所有行星轨道的半长轴的三次方跟公转周期的二次方的比值都相等”的科学家是( )
A.牛顿 B.第谷
C.开普勒 D.哥白尼
2.关于天体的运动,下列说法正确的是( )
A.太阳位于所有行星的圆轨道的圆心处
B.天体的运动是最完美、最和谐的匀速圆周运动
C.太阳从东边升起,从西边落下,所以太阳绕地球运动
D.太阳系中所有行星都绕太阳运动
3.太阳系有八大行星,八大行星离地球的远近不同,绕太阳运转的周期也不相同。下列反映周期与轨道半径关系的图像正确的是( )
4.开普勒的行星运动规律也适用于其他行星或人造卫星的运动,某一人造卫星绕地球做匀速圆周运动,其轨道半径为月球绕地球轨道半径的,则此卫星运行的周期在下面哪个范围内( )
A.1~4天
B.4~8天
C.8~16天
D.16~20天
5.地球公转轨道的半径在天文学上常用来作为长度单位,叫作天文单位,用来量度太阳系内行星与太阳的距离。已知火星公转的周期是1.84年,根据开普勒第三定律,火星公转轨道半径是多少天文单位 (将地球和火星绕太阳公转的轨道近似成圆形轨道。)
6.土星直径为119 300 km,是太阳系中第二大行星,其自转周期为10 h 39 min,公转周期为29.4年,距离太阳1.432×109 km。土星最引人注目的是绕着其赤道的巨大光环。在地球上人们只需要一架小型望远镜就能清楚地看到光环,环的外沿直径约为274 000 km。请由上面提供的信息,估算地球距太阳有多远。(保留3位有效数字)
提升练
1.某行星绕太阳沿椭圆轨道运行,如图所示,在这颗行星的轨道上有a、b、c、d四个对称点,若行星运动周期为T,则该行星( )
A.从a到b的运动时间等于从c到d的运动时间
B.从d经a到b的运动时间等于从b经c到d的运动时间
C.从a到b的时间tab>
D.从c到d的时间tcd>
2.如图所示,某行星沿椭圆轨道运行,远日点离太阳的距离为a,近日点离太阳的距离为b,过远日点时行星的速率为va,则过近日点时的速率为( )
A.vb=va B.vb=va
C.vb=va D.vb=va
3.对开普勒第一定律的理解,下列说法正确的是( )
A.在行星绕太阳运动一周的时间内,它离太阳的距离是不变的
B.在行星绕太阳运动一周的时间内,它离太阳的距离是变化的
C.太阳不一定在所有行星运动椭圆轨迹的焦点上
D.某个行星绕太阳运动的轨道一定不在一个固定的平面内
4.2016年8月16日凌晨,被命名为墨子号的中国首颗量子科学实验卫星开启星际之旅,其运行轨道为如图所示的椭圆轨道,地球E位于椭圆的一个焦点上。轨道上标记了墨子卫星经过相等时间间隔(Δt=,T为轨道周期)的位置。下列说法正确的是( )
A.面积S1>S2
B.卫星在轨道A点的速度小于在B点的速度
C.T2=Ca3,其中C为常数,a为椭圆半长轴
D.T2=C'b3,其中C'为常数,b为椭圆半短轴
5.月球环绕地球运动的轨道半径约为地球半径的60倍,运行周期约为27天。应用开普勒定律计算:在赤道平面内离地多高时,人造地球卫星随地球一起转动,就像停留在天空中一样。结果保留三位有效数字,取R地=6 400 km。
6.地球的公转轨道接近圆,但彗星的运动轨道则是一个非常扁的椭圆,天文学家哈雷曾经在1682年跟踪过一颗彗星,他算出这颗彗星轨道的半长轴约等于地球轨道半径的18倍,并预言这颗彗星将每隔一定时间就会出现,哈雷的预言得到证实,该彗星被命名为哈雷彗星。哈雷彗星最近出现的时间是1986年,请你根据开普勒第三定律即=k,其中T为行星绕太阳公转的周期,r为轨道的半长轴估算,如果忽略其他影响,它下次飞近地球大约在哪一年
参考答案:
基础练
1.发现“所有行星轨道的半长轴的三次方跟公转周期的二次方的比值都相等”的科学家是( )
A.牛顿 B.第谷
C.开普勒 D.哥白尼
解析:所有行星轨道的半长轴的三次方跟公转周期的二次方的比值都相等,也就是开普勒第三定律,是开普勒发现的。
答案:C
2.关于天体的运动,下列说法正确的是( )
A.太阳位于所有行星的圆轨道的圆心处
B.天体的运动是最完美、最和谐的匀速圆周运动
C.太阳从东边升起,从西边落下,所以太阳绕地球运动
D.太阳系中所有行星都绕太阳运动
解析:天体的运动轨道都是椭圆,而不是圆,故A、B错误。太阳从东边升起,又从西边落下,是地球自转的结果,故C错误。
答案:D
3.太阳系有八大行星,八大行星离地球的远近不同,绕太阳运转的周期也不相同。下列反映周期与轨道半径关系的图像正确的是( )
解析:由开普勒第三定律知=k,所以R3=kT2,D正确。
答案:D
4.开普勒的行星运动规律也适用于其他行星或人造卫星的运动,某一人造卫星绕地球做匀速圆周运动,其轨道半径为月球绕地球轨道半径的,则此卫星运行的周期在下面哪个范围内( )
A.1~4天
B.4~8天
C.8~16天
D.16~20天
解析:由开普勒第三定律=k,得,所以T星=T月=×27天=5.2天,B正确。
答案:B
5.地球公转轨道的半径在天文学上常用来作为长度单位,叫作天文单位,用来量度太阳系内行星与太阳的距离。已知火星公转的周期是1.84年,根据开普勒第三定律,火星公转轨道半径是多少天文单位 (将地球和火星绕太阳公转的轨道近似成圆形轨道。)
解析:设地球和火星的轨道半径分别为r1、r2,公转周期分别为T1、T2。
根据开普勒第三定律得,
得r2=·r1=1.5天文单位。
答案:1.5
6.土星直径为119 300 km,是太阳系中第二大行星,其自转周期为10 h 39 min,公转周期为29.4年,距离太阳1.432×109 km。土星最引人注目的是绕着其赤道的巨大光环。在地球上人们只需要一架小型望远镜就能清楚地看到光环,环的外沿直径约为274 000 km。请由上面提供的信息,估算地球距太阳有多远。(保留3位有效数字)
解析:根据开普勒第三定律有=k,k只与太阳质量有关。则,其中T为公转周期,R为行星到太阳的距离。代入数值,解得R地=1.50×1011m=1.50×108km。
答案:约1.50×108 km
提升练
1.某行星绕太阳沿椭圆轨道运行,如图所示,在这颗行星的轨道上有a、b、c、d四个对称点,若行星运动周期为T,则该行星( )
A.从a到b的运动时间等于从c到d的运动时间
B.从d经a到b的运动时间等于从b经c到d的运动时间
C.从a到b的时间tab>
D.从c到d的时间tcd>
解析:根据开普勒第二定律知行星在近日点速度最大,远日点速度最小。行星由a到b运动的平均速度大于由c到d运动的平均速度,而弧长ab等于弧长cd,故A错误;同理可知B错误;在整个椭圆轨道上tab=tda<,tcd=tbc>,故C错误,D正确。
答案:D
2.如图所示,某行星沿椭圆轨道运行,远日点离太阳的距离为a,近日点离太阳的距离为b,过远日点时行星的速率为va,则过近日点时的速率为( )
A.vb=va B.vb=va
C.vb=va D.vb=va
解析:若行星从轨道的A点经足够短的时间t运动到A'点,则与太阳的连线扫过的面积可看作扇形,其面积SA=;若行星从轨道的B点也经时间t运动到B'点,则与太阳的连线扫过的面积SB=;根据开普勒第二定律得,即vb=va,C正确。
答案:C
3.对开普勒第一定律的理解,下列说法正确的是( )
A.在行星绕太阳运动一周的时间内,它离太阳的距离是不变的
B.在行星绕太阳运动一周的时间内,它离太阳的距离是变化的
C.太阳不一定在所有行星运动椭圆轨迹的焦点上
D.某个行星绕太阳运动的轨道一定不在一个固定的平面内
解析:根据开普勒第一定律的内容可以判定,行星绕太阳运动的轨道是椭圆,有时远离太阳,行星有时靠近太阳,所以它离太阳的距离是变化的,A错误,B正确;太阳一定在所有行星运动的椭圆轨迹的焦点上,C错误;行星绕太阳运动的轨道一定在一个固定的平面内,D错误。
答案:B
4.2016年8月16日凌晨,被命名为墨子号的中国首颗量子科学实验卫星开启星际之旅,其运行轨道为如图所示的椭圆轨道,地球E位于椭圆的一个焦点上。轨道上标记了墨子卫星经过相等时间间隔(Δt=,T为轨道周期)的位置。下列说法正确的是( )
A.面积S1>S2
B.卫星在轨道A点的速度小于在B点的速度
C.T2=Ca3,其中C为常数,a为椭圆半长轴
D.T2=C'b3,其中C'为常数,b为椭圆半短轴
解析:根据开普勒第二定律可知,卫星与地球的连线在相同时间内扫过的面积相等,故面积S1=S2,选项A错误;根据开普勒第二定律可知,卫星在轨道A点的速度大于在B点的速度,选项B错误;根据开普勒第三定律可知=C,故选项C正确,D错误。
答案:C
5.月球环绕地球运动的轨道半径约为地球半径的60倍,运行周期约为27天。应用开普勒定律计算:在赤道平面内离地多高时,人造地球卫星随地球一起转动,就像停留在天空中一样。结果保留三位有效数字,取R地=6 400 km。
解析:月球和人造地球卫星都环绕地球运动,故可用开普勒第三定律求解。当人造地球卫星相对地球不动时,人造地球卫星的周期与地球自转周期相同。
设人造地球卫星轨道半径为R、周期为T。
根据题意知月球轨道半径为60R地,
周期为T0=27天,则有
,整理得
R=×60R地=×60R地=6.67R地。
卫星离地高度h=R-R地=5.67R地=5.67×6400km=3.63×104km。
答案:3.63×104 km
6.地球的公转轨道接近圆,但彗星的运动轨道则是一个非常扁的椭圆,天文学家哈雷曾经在1682年跟踪过一颗彗星,他算出这颗彗星轨道的半长轴约等于地球轨道半径的18倍,并预言这颗彗星将每隔一定时间就会出现,哈雷的预言得到证实,该彗星被命名为哈雷彗星。哈雷彗星最近出现的时间是1986年,请你根据开普勒第三定律即=k,其中T为行星绕太阳公转的周期,r为轨道的半长轴估算,如果忽略其他影响,它下次飞近地球大约在哪一年
解析:=k,其中T为行星绕太阳公转的周期,r为轨道的半长轴,k是对太阳系中的任何行星都适用的常量。可以根据已知条件列方程求解。
将地球的公转轨道近似成圆形轨道,其周期为T1,半径为r1;哈雷彗星的周期为T2,轨道半长轴为r2,则根据开普勒第三定律有
因为r2=18r1,地球公转周期为1年,所以可知哈雷彗星的周期为
T2=×T1=76.4年
所以它下次飞近地球大约是在2062年。
答案:2062年
