人教新课标A版必修5第三章 不等式 单元练习(含答案)
文档属性
| 名称 | 人教新课标A版必修5第三章 不等式 单元练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 111.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 15:03:50 | ||
图片预览




文档简介
人教新课标A版必修5第三章
不等式
一、单选题
1.(2021高二下·杭州期中)已知实数 , 满足 ,设 ,则 的最大值为( )
A. 6 B. 3 C. 0 D. -3
2.(2019高二上·阳江月考)已知x、y满足条件 则2x+4y的最小值为( )
A. -6 B. 6 C. 12 D. -12
3.(2020高一下·大庆期中)若不等式 对一切 恒成立,则实数a取值的集合( )
A. B. C. D.
4.(2020高一下·宣城月考)若 , , ,则 的最小值为( )
A. B. 4 C. D. 3
5.(2019高一上·重庆月考)已知不等式 的解集为 ,则不等式 的解集为( )
A. B. C. D.
6.(2019高三上·安徽月考)已知正数 , 满足 ,则 的最小值是( )
A. 2 B. 3 C. 4 D. 5
7.(2019高一下·大庆期中)已知正项等比数列 的公比为 ,若 ,则 的最小值等于( )
A. B. C. D.
8.(2020高一上·泉州月考)若两个正实数 满足 ,且不等式 有解,则实数 的取值范围是( )
A. B. 或
C. D. 或
9.(2019高一下·广东期中)在 中, , 分别为 , 的中点, 为 上的任一点,实数 , 满足 ,设 、 、 、 的面积分别为 、 、 、 ,记 ( ),则 取到最大值时, 的值为( )
A. -1 B. 1 C. D.
二、填空题
10.(2020高二上·峨山月考)设 满足约束条件 则 的最大值为 .
11.(2020高一上·南京月考)设集合 中的最大、最小元素分别为M、m,则 的值是________,当x取最小元素m时, 的值是________.
12.(2021高一下·抚州期末)设 , ,且 恒成立,则n的最大值为 .
13.(2020高一上·上海期中)已知关于 的不等式 解集为空集,则实数 的取值范围是________
14.(2019高一下·合肥期中)已知实数 , 满足不等式组 ,则 的最小值为________.
15.(2019高二上·蛟河期中)已知 则 的最小值是________.
16.(2019高三上·镇江期中)若 ,则 的最小值是 .
17.(2019高一下·黑龙江月考)若函数 有两个极值点 ,其中 ,且 ,则方程 的实根个数为________.
18.(2020高二上·徐州期中)若 ,且 ,则 的最小值为________.
三、解答题
19.(2020高一上·启东月考)经过长期观测得到:在交通繁忙的时段内某公路汽车的车流量 (千辆/时)与汽车的平均速度 (千米/时)之间的函数关系为 .
(1)在该时段内,当汽车的平均速度 为多少时,车流量最大?最大车流量是多少(精确到 千辆/时)?
(2)若要求在该时段内车流量超过 千辆/时,则汽车的平均速度应该在什么范围内?
20.(2019高一上·长沙月考)某工厂去年的某产品的年销售量为100万只,每只产品的销售价为10元,每只产品固定成本为8元.今年,工厂第一次投入100万元(科技成本),并计划以后每年比上一年多投入100万元(科技成本),预计销售量从今年开始每年比上一年增加10万只,第n次投入后,每只产品的固定成本为 (k>0,k为常数, 且n≥0),若产品销售价保持不变,第n次投入后的年利润为 万元.
(Ⅰ)求k的值,并求出 的表达式;
(Ⅱ)若今年是第1年,问第几年年利润最高 最高利润为多少万元
(2019高一上·上海月考)若抛物线 与x轴的两个交点在y轴的同侧,求实数a的取值范围.
22.(2020高一上·金华期末)已知函数 是奇函数, .
(1)求 的值;
(2)对任意的 ,不等式 恒成立,求实数 的取值范围.
答案解析部分
一、单选题
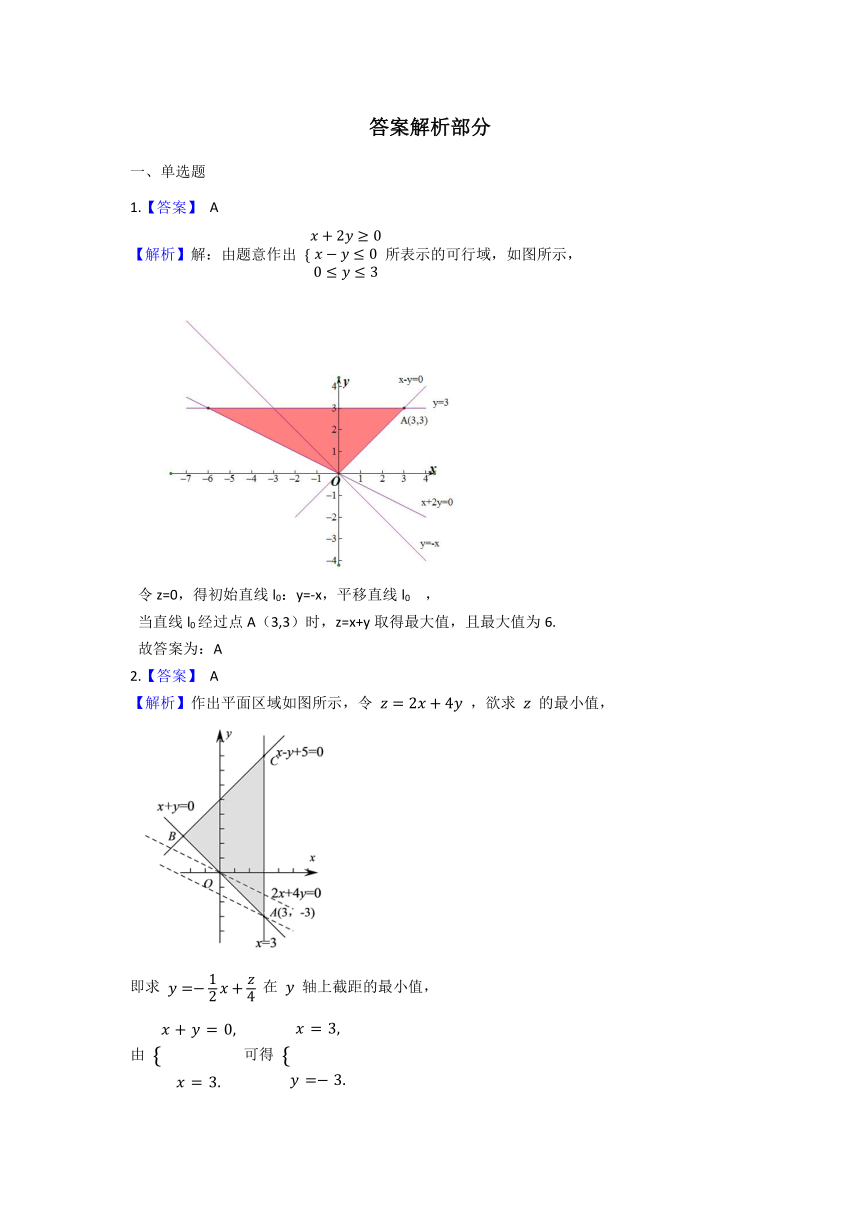
1.【答案】 A
【解析】解:由题意作出 所表示的可行域,如图所示,
令z=0,得初始直线l0:y=-x,平移直线l0 ,
当直线l0经过点A(3,3)时,z=x+y取得最大值,且最大值为6.
故答案为:A
2.【答案】 A
【解析】作出平面区域如图所示,令 ,欲求 的最小值,
即求 在 轴上截距的最小值,
由 可得
平移直线 ,
可以看出当直线过点 时,纵截距最小,
,
故答案为:A.
3.【答案】 C
【解析】解:① 时,不等式化为 对一切 恒成立,因此 满足题意;
② 时,要使不等式 对一切 恒成立,则必有 解得 .
综上①②可知:实数a取值的集合是 .
故答案为:C.
4.【答案】 A
【解析】解:∵ ,∴
∴ ,
当且仅当 即 , 时,取等号,
故答案为:A.
5.【答案】 B
【解析】 可化为:
可得
不等式 的解集为
, 是方程
代入
得: 即
即
根据用数轴标根法可得: 或
不等式 的解集为:
故答案为:B.
6.【答案】 A
【解析】设 ,则
(当且仅当 ,即 时取等号)
且 ,解得: ,即
的最小值为
故选:
7.【答案】 C
【解析】∵正项等比数列 的公比为3,且
∴
∴
∴ ,当且仅当 时取等号,
故答案为:C.
8.【答案】 B
【解析】因为 ,
取等号时 ,所以 ,
因为不等式 有解,所以 ,
所以 或 ,
故答案为:B.
9.【答案】 D
【解析】如图所示:
因为 是△ 的中位线,
所以 到 的距离等于△ 的 边上高的一半,
所以 ,
由此可得 ,
当且仅当 时,即 为 的中点时,等号成立,
所以 ,
由平行四边形法则可得 , ,
将以上两式相加可得 ,
所以 ,
又已知 ,
根据平面向量基本定理可得 ,
从而 .
故答案为:D.
二、填空题
10.【答案】 14
【解析】由约束条件 作出可行域,
化目标函数 为
,
由图可知,当直线 过点 时,直线在 轴上的截距最小,
有最大值为:14
故答案为:14
11.【答案】 ;
【解析】 ,
取最小值为1,b取最大值为2.
所以最大值 ,
又 ,
当且仅当 时取到等号,
即 时,
有最小值 ,
所以 ,
当x取最小元素m时 的值是 .
故答案为: , .
12.【答案】 4
【解析】解:由 ,可得 , , ,
由 ,可得 ,
则
,
当 时,上式取得等号,
由题意可得 ,
即 的最大值为4.
故答案为:4.
13.【答案】 [0,4)
【解析】由题意,关于 的不等式 解集为空集,
当 时,不等式 ,此时解集为空集,符合题意;
当 时,要使得不等式 解集为空集,则满足 ,
解得 ,
综上可得,实数 的取值范围是[0,4).
故答案为:[0,4).
14.【答案】 -6
【解析】解:由题得不等式组对应的平面区域为如图所示的△ABC,
当直线 经过点A(0,3)时,直线的纵截距 最大,z最小,所以 故填-6。
15.【答案】 1
【解析】根据限制条件画出可行域,如图所示,可知 内部含边界是可行域,
将目标函数 ,转化成 ,可知 是斜率为 的一簇平行线在 轴上截距,所以过 点时, 最小.
解 ,得 ,代入到 得 的最小值是 .
16.【答案】 25
【解析】解:由 ,得
所以 ,可得 .
则 ,当且仅当 时取等号.
故答案为:25.
17.【答案】 5
【解析】∵函数f(x)=﹣lnx+ax2+bx﹣a﹣2b有两个极值点x1 , x2 ,
∴f′(x)=﹣ +2ax+b= ,
即为2ax2+bx﹣1=0有两个不相等的正根,
∴△=b2+8a>0.解得x= .
∵x1<x2 , ﹣ ,b>0,
∴x1= ,x2= .
而方程2a(f(x))2+bf(x)﹣1=0的△1=△>0,
∴此方程有两解且f(x)=x1或x2
即有0<x1<x2 , :∵x1 , x2>0又x1x2=﹣ >1
∴x2>1,∵f(1)=﹣b<0∴f(x1)<0,
f(x2)>0.
①根据f′(x)画出f(x)的简图,
∵f(x2)=x2 , 由图象可知方程f(x)=x2有两解,方程f(x)=x1有三解.
综上①②可知:方程f(x)=x1或f(x)=x2共有5个实数解.
即关于x的方程2a(f(x))2+bf(x)﹣1=0的共有5不同实根.
故答案为:5
18.【答案】
【解析】令 ,则
, ,即 ,
, , ,
当 取得最小值时, 也取得最小值,
又 ,当且仅当 ,即 时,等号成立,
,即 的最小值为 ,
故答案为: 。
三、解答题
19.【答案】 (1)解:依题意 ,当且仅当 等号成立,
最大车流量 (千辆/时);
(2)解:由条件得 ,整理得 ,解得 .
故汽车的平均速度应该在 范围内.
20.【答案】 解:(Ⅰ)由 ,当n=0时,由题意,可得k=8,
所以 .
(Ⅱ)由
.
当且仅当 ,即n=8时取等号,
所以第8年工厂的利润最高,最高为520万元.
21.【答案】 解:设 的两根为 ,
由题得 ,(1), ,(2),
解(1)(2)得 或 .
所以实数 的取值范围为 .
22.【答案】 (1)解: ,
则 或 ,
因为 是奇函数,
故 , ,
即 ,
所以 ;
(2)解: ,
令 , ,
所以 , .
易知 ,当 时取等号,
所以 ,
又由 ,
故 ,
所以 .
不等式
一、单选题
1.(2021高二下·杭州期中)已知实数 , 满足 ,设 ,则 的最大值为( )
A. 6 B. 3 C. 0 D. -3
2.(2019高二上·阳江月考)已知x、y满足条件 则2x+4y的最小值为( )
A. -6 B. 6 C. 12 D. -12
3.(2020高一下·大庆期中)若不等式 对一切 恒成立,则实数a取值的集合( )
A. B. C. D.
4.(2020高一下·宣城月考)若 , , ,则 的最小值为( )
A. B. 4 C. D. 3
5.(2019高一上·重庆月考)已知不等式 的解集为 ,则不等式 的解集为( )
A. B. C. D.
6.(2019高三上·安徽月考)已知正数 , 满足 ,则 的最小值是( )
A. 2 B. 3 C. 4 D. 5
7.(2019高一下·大庆期中)已知正项等比数列 的公比为 ,若 ,则 的最小值等于( )
A. B. C. D.
8.(2020高一上·泉州月考)若两个正实数 满足 ,且不等式 有解,则实数 的取值范围是( )
A. B. 或
C. D. 或
9.(2019高一下·广东期中)在 中, , 分别为 , 的中点, 为 上的任一点,实数 , 满足 ,设 、 、 、 的面积分别为 、 、 、 ,记 ( ),则 取到最大值时, 的值为( )
A. -1 B. 1 C. D.
二、填空题
10.(2020高二上·峨山月考)设 满足约束条件 则 的最大值为 .
11.(2020高一上·南京月考)设集合 中的最大、最小元素分别为M、m,则 的值是________,当x取最小元素m时, 的值是________.
12.(2021高一下·抚州期末)设 , ,且 恒成立,则n的最大值为 .
13.(2020高一上·上海期中)已知关于 的不等式 解集为空集,则实数 的取值范围是________
14.(2019高一下·合肥期中)已知实数 , 满足不等式组 ,则 的最小值为________.
15.(2019高二上·蛟河期中)已知 则 的最小值是________.
16.(2019高三上·镇江期中)若 ,则 的最小值是 .
17.(2019高一下·黑龙江月考)若函数 有两个极值点 ,其中 ,且 ,则方程 的实根个数为________.
18.(2020高二上·徐州期中)若 ,且 ,则 的最小值为________.
三、解答题
19.(2020高一上·启东月考)经过长期观测得到:在交通繁忙的时段内某公路汽车的车流量 (千辆/时)与汽车的平均速度 (千米/时)之间的函数关系为 .
(1)在该时段内,当汽车的平均速度 为多少时,车流量最大?最大车流量是多少(精确到 千辆/时)?
(2)若要求在该时段内车流量超过 千辆/时,则汽车的平均速度应该在什么范围内?
20.(2019高一上·长沙月考)某工厂去年的某产品的年销售量为100万只,每只产品的销售价为10元,每只产品固定成本为8元.今年,工厂第一次投入100万元(科技成本),并计划以后每年比上一年多投入100万元(科技成本),预计销售量从今年开始每年比上一年增加10万只,第n次投入后,每只产品的固定成本为 (k>0,k为常数, 且n≥0),若产品销售价保持不变,第n次投入后的年利润为 万元.
(Ⅰ)求k的值,并求出 的表达式;
(Ⅱ)若今年是第1年,问第几年年利润最高 最高利润为多少万元
(2019高一上·上海月考)若抛物线 与x轴的两个交点在y轴的同侧,求实数a的取值范围.
22.(2020高一上·金华期末)已知函数 是奇函数, .
(1)求 的值;
(2)对任意的 ,不等式 恒成立,求实数 的取值范围.
答案解析部分
一、单选题
1.【答案】 A
【解析】解:由题意作出 所表示的可行域,如图所示,
令z=0,得初始直线l0:y=-x,平移直线l0 ,
当直线l0经过点A(3,3)时,z=x+y取得最大值,且最大值为6.
故答案为:A
2.【答案】 A
【解析】作出平面区域如图所示,令 ,欲求 的最小值,
即求 在 轴上截距的最小值,
由 可得
平移直线 ,
可以看出当直线过点 时,纵截距最小,
,
故答案为:A.
3.【答案】 C
【解析】解:① 时,不等式化为 对一切 恒成立,因此 满足题意;
② 时,要使不等式 对一切 恒成立,则必有 解得 .
综上①②可知:实数a取值的集合是 .
故答案为:C.
4.【答案】 A
【解析】解:∵ ,∴
∴ ,
当且仅当 即 , 时,取等号,
故答案为:A.
5.【答案】 B
【解析】 可化为:
可得
不等式 的解集为
, 是方程
代入
得: 即
即
根据用数轴标根法可得: 或
不等式 的解集为:
故答案为:B.
6.【答案】 A
【解析】设 ,则
(当且仅当 ,即 时取等号)
且 ,解得: ,即
的最小值为
故选:
7.【答案】 C
【解析】∵正项等比数列 的公比为3,且
∴
∴
∴ ,当且仅当 时取等号,
故答案为:C.
8.【答案】 B
【解析】因为 ,
取等号时 ,所以 ,
因为不等式 有解,所以 ,
所以 或 ,
故答案为:B.
9.【答案】 D
【解析】如图所示:
因为 是△ 的中位线,
所以 到 的距离等于△ 的 边上高的一半,
所以 ,
由此可得 ,
当且仅当 时,即 为 的中点时,等号成立,
所以 ,
由平行四边形法则可得 , ,
将以上两式相加可得 ,
所以 ,
又已知 ,
根据平面向量基本定理可得 ,
从而 .
故答案为:D.
二、填空题
10.【答案】 14
【解析】由约束条件 作出可行域,
化目标函数 为
,
由图可知,当直线 过点 时,直线在 轴上的截距最小,
有最大值为:14
故答案为:14
11.【答案】 ;
【解析】 ,
取最小值为1,b取最大值为2.
所以最大值 ,
又 ,
当且仅当 时取到等号,
即 时,
有最小值 ,
所以 ,
当x取最小元素m时 的值是 .
故答案为: , .
12.【答案】 4
【解析】解:由 ,可得 , , ,
由 ,可得 ,
则
,
当 时,上式取得等号,
由题意可得 ,
即 的最大值为4.
故答案为:4.
13.【答案】 [0,4)
【解析】由题意,关于 的不等式 解集为空集,
当 时,不等式 ,此时解集为空集,符合题意;
当 时,要使得不等式 解集为空集,则满足 ,
解得 ,
综上可得,实数 的取值范围是[0,4).
故答案为:[0,4).
14.【答案】 -6
【解析】解:由题得不等式组对应的平面区域为如图所示的△ABC,
当直线 经过点A(0,3)时,直线的纵截距 最大,z最小,所以 故填-6。
15.【答案】 1
【解析】根据限制条件画出可行域,如图所示,可知 内部含边界是可行域,
将目标函数 ,转化成 ,可知 是斜率为 的一簇平行线在 轴上截距,所以过 点时, 最小.
解 ,得 ,代入到 得 的最小值是 .
16.【答案】 25
【解析】解:由 ,得
所以 ,可得 .
则 ,当且仅当 时取等号.
故答案为:25.
17.【答案】 5
【解析】∵函数f(x)=﹣lnx+ax2+bx﹣a﹣2b有两个极值点x1 , x2 ,
∴f′(x)=﹣ +2ax+b= ,
即为2ax2+bx﹣1=0有两个不相等的正根,
∴△=b2+8a>0.解得x= .
∵x1<x2 , ﹣ ,b>0,
∴x1= ,x2= .
而方程2a(f(x))2+bf(x)﹣1=0的△1=△>0,
∴此方程有两解且f(x)=x1或x2
即有0<x1<x2 , :∵x1 , x2>0又x1x2=﹣ >1
∴x2>1,∵f(1)=﹣b<0∴f(x1)<0,
f(x2)>0.
①根据f′(x)画出f(x)的简图,
∵f(x2)=x2 , 由图象可知方程f(x)=x2有两解,方程f(x)=x1有三解.
综上①②可知:方程f(x)=x1或f(x)=x2共有5个实数解.
即关于x的方程2a(f(x))2+bf(x)﹣1=0的共有5不同实根.
故答案为:5
18.【答案】
【解析】令 ,则
, ,即 ,
, , ,
当 取得最小值时, 也取得最小值,
又 ,当且仅当 ,即 时,等号成立,
,即 的最小值为 ,
故答案为: 。
三、解答题
19.【答案】 (1)解:依题意 ,当且仅当 等号成立,
最大车流量 (千辆/时);
(2)解:由条件得 ,整理得 ,解得 .
故汽车的平均速度应该在 范围内.
20.【答案】 解:(Ⅰ)由 ,当n=0时,由题意,可得k=8,
所以 .
(Ⅱ)由
.
当且仅当 ,即n=8时取等号,
所以第8年工厂的利润最高,最高为520万元.
21.【答案】 解:设 的两根为 ,
由题得 ,(1), ,(2),
解(1)(2)得 或 .
所以实数 的取值范围为 .
22.【答案】 (1)解: ,
则 或 ,
因为 是奇函数,
故 , ,
即 ,
所以 ;
(2)解: ,
令 , ,
所以 , .
易知 ,当 时取等号,
所以 ,
又由 ,
故 ,
所以 .
