人教新课标A版必修2 综合复习与测试(含答案)
文档属性
| 名称 | 人教新课标A版必修2 综合复习与测试(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 354.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 00:00:00 | ||
图片预览




文档简介
人教新课标A版必修2
综合复习与测试
一、单选题
1.(2020高二上·遵义月考)若直线经过 两点,则直线 的倾斜角为( )
A. 30 B. 45 C. 60 D. 120
2.(2019高二下·青浦期末)已知空间不重合的三条直线l、m、n及一个平面 ,下列命题中的假命题是( ).
A. 若 , ,则 B. 若 , ,则
C. 若 , ,则 D. 若 , ,则
3.(2020高三上·宁波期末)如图,正方体 中, ,点 在侧面 内.若 ,则点 的轨迹为( )
A. 线段 B. 圆弧 C. 抛物线一部分 D. 椭圆一部分
4.(2019高一下·韶关期末)如图是正方体的展开图,则在这个正方体中:
① 与 平行;② 与 是异面直线;③ 与 成60°角;④ 与 垂直.以上四个命题中,正确命题的序号是( )
A. ①②③ B. ②④ C. ③④ D. ②③④
5.(2019高一下·韶关期末)已知直线 与圆 交于A、B两点,O是坐标原点,向量 、 满足 ,则实数a的值是( )
A. 2 B. -2 C. 或 D. 2或-2
6.(2019·云南模拟)已知直三棱柱 的顶点都在球 的球面上, , ,若球 的表面积为 ,则这个直三棱柱的体积是( )
A. 16 B. 15 C. D.
7.(2020高二上·朝阳期末)如图,将边长为4的正方形折成一个正四棱柱的侧面,则异面直线AK和LM所成角的大小为( )
A. 30° B. 45° C. 60° D. 90°
8.(2021高三上·河南月考)我国南北朝时期的数学家祖暅提出了一个原理“幂势既同,则积不容异”,即夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.现有某几何体和一个圆锥满足祖暅原理的条件,若该圆锥的侧面展开图是半径为2的一个半圆,则该几何体的体积为( )
A. B. C. D.
9.(2020·江西模拟)在平面五边形 中, , , , ,且 .将五边形 沿对角线 折起,使平面 与平面 所成的二面角为 ,则沿对角线 折起后所得几何体的外接球的表面积为( )
A. B. C. D.
10.(2019高三上·广东月考)已知三棱锥 的四个顶点在球 的球面上,点 分别是 的中点, ,则球 的表面积为( )
A. B. C. D.
11.(2019高三上·柳州月考)已知三棱锥 的四个顶点均在球 的球面上, 和 所在平面互相垂直, , , ,则球 的体积为( )
A. B. C. D.
二、填空题
12.点 关于直线 的对称点是 , 关于原点O的对称点是 ,则 ________.
13.(2020高二上·重庆月考)已知△ABC和直线l,若l⊥AB,l⊥BC,则l和AC的关系是________.
14.(2020高二上·四川月考)α、β是两个不同的平面,m、n是平面α及β之外的两条不同直线,
给出四个论断:
① m ^ n ②α^β ③ m ^β ④ n ^α
以其中三个论断作为条件,余下一个论断作为结论,写出你认为
正确的一个命题:________.
15.(2020高二上·成都月考)已知直线 和圆 相交于 、 两点,则弦长 ________.
16.(2021·衡阳模拟)设圆锥的顶点为 , 为圆锥底面圆 的直径,点 为圆 上的一点(异于 、 ),若 ,三棱锥 的外接球表面积为 ,则圆锥的体积为 .
17.(2020高二上·安徽期中)在平行四边形ABCD中, , ,将此平行四边形沿对角线BD折叠,使平面 平面CBD,则三棱锥A-BCD外接球的体积是________.
18.(2019高三上·杨浦期中)已知圆锥的侧面展开图是一个扇形,若此扇形的圆心角为 、面积为 ,则该圆锥的体积为 .
19.(2019·全国Ⅱ卷理)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为________.
20.(2020高三上·兴宁期末)已知空间四边形 中, , , ,若平面 平面 ,则该几何体的外接球表面积为________.
三、解答题
21.(2020·盐城模拟)在极坐标系中,已知圆 和直线 相交于 两点,求线段 的长.
22.(2019高一下·广东期末)已知直线 : ,过点 且圆心在x轴上的圆C与y轴相切.
(1)求圆C的方程;
(2)求直线l被圆C截得的弦长.
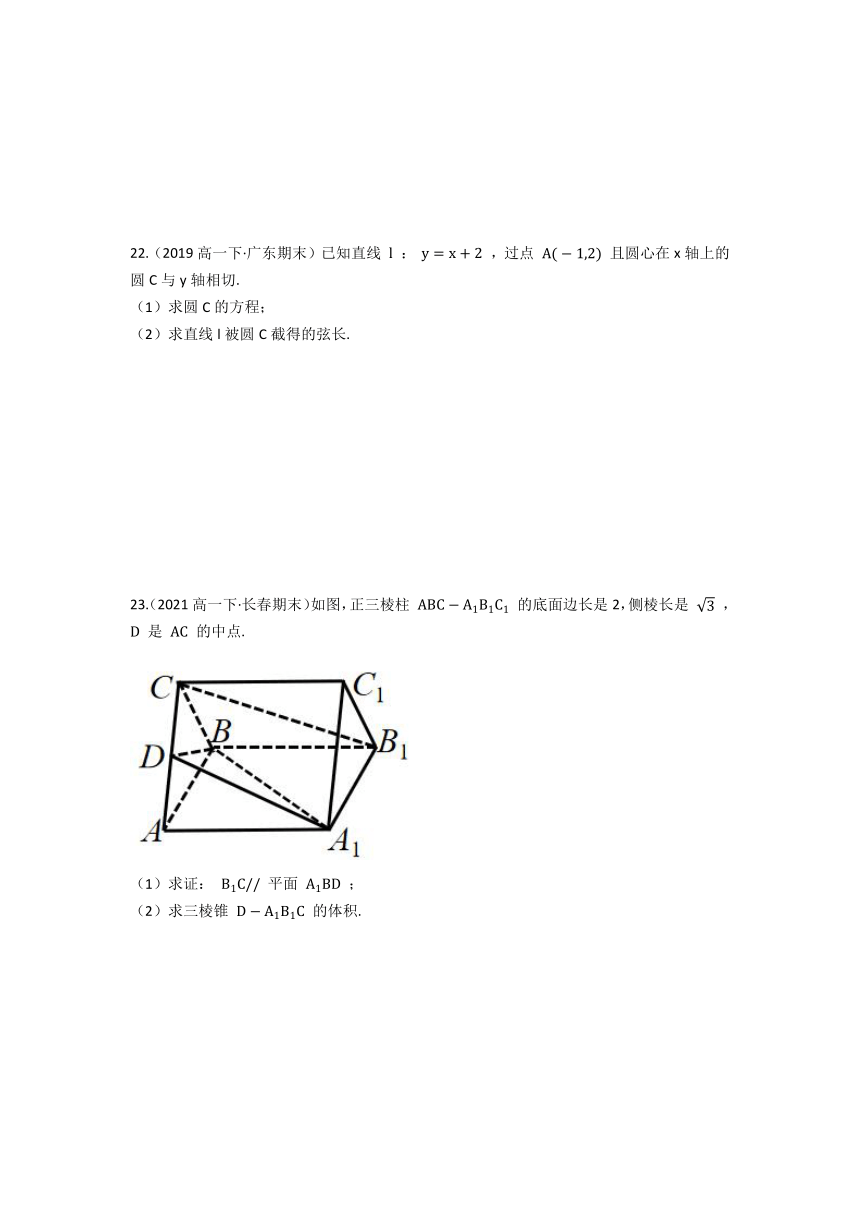
23.(2021高一下·长春期末)如图,正三棱柱 的底面边长是2,侧棱长是 , 是 的中点.
(1)求证: 平面 ;
(2)求三棱锥 的体积.
24.(2019高一下·石河子月考)如图,
(I)求证
(II)设
答案解析部分
一、单选题
1.【答案】 A
【解析】设直线AB的倾斜角为 ,由两点斜率公式的直线AB的斜率 所以 ,
故答案为:A.
2.【答案】 B
【解析】对于A选项,根据平行公理可知,A选项正确.
对于B选项,两条直线平行与同一个平面,这两条直线可以相交、平行或异面,B选项是假命题.
对于C选项,由于 , ,根据空间角的定义可知, ,C选项正确.
对于D选项,由于 ,所以 平行于平面 内一条直线 ,而 ,所以 ,所以 ,即D选项正确.
故答案为:B.
3.【答案】 A
【解析】如图建立空间直角坐标系,
设棱长为3, , , , , , ,
,整理为: ,
所以点 的轨迹方程是关于 的二元一次方程,所以点M的轨迹是平面 平面内,直线 内的一段线段。
故答案为:A
4.【答案】 C
【解析】将正方体的展开图还原为正方体ABCD﹣EFMN后,
可得AF,CN异面;BM,AN平行;
连接AN,NF,可得∠FAN为AF,BM所成角,且为60°;
BN⊥DE,DE⊥AB可得DE⊥平面ABN,可得DE⊥BN,
可得③④正确,
故答案为:C.
5.【答案】 D
【解析】由 ,两边平方,得 ,
所以 ,则 为等腰直角三角形,
而圆 的半径AO=2,
则原点O到直线x+y=a的距离为 ,
所以 ,解得a的值为2或-2。
故答案为:D.
6.【答案】 A
【解析】由题, ,
因为 , ,易知三角形ABC为等腰直角三角形,
故三棱柱的高
故体积
故答案为:A
7.【答案】 D
【解析】由题知,折叠后的正四棱锥如图所示,
易知K为 的四等分点,L为 的中点,M为 的四等分点, ,
取 的中点N,易证 ,
则异面直线AK和LM所成角即直线AK和KN所成角 ,
在 中, , ,
故
故答案为:D
8.【答案】 C
【解析】圆锥底面周长为 ,
所以圆锥的底面半径 ,圆锥的高 ,
所以圆锥的体积为 ,
由祖暅原理,该几何体的体积也为 .
故答案为:C
9.【答案】 C
【解析】设 的中心为 ,矩形 的中心为 ,
过 作垂直于平面 的直线 ,
过 作垂直于平面 的直线 ,
则由球的性质可知,直线 与 的交点 ,
即几何体 外接球的球心..取 的中点 ,
连接 , ,由条件得 ,
.连接 ,因为 ,
从而 .连接 ,则 为所得几何体外接球的半径.
又 ,则 ,
故所得几何体外接球的表面积等于 .
故答案为:C.
10.【答案】 C
【解析】
,
平面 平面 ,
点 分别是 的中点, ,
设球 半径为
,
故答案为:C
11.【答案】 D
【解析】解:
, , ,
,
,
的外接圆的半径为
和 所在平面互相垂直,
球心在 边的高上,
设球心到平面 的距离为 ,
则
,
球 体积 .
故答案为:D
二、填空题
12.【答案】
【解析】因为点 关于直线 的对称点是
所以 ,
又因为 关于原点O的对称点是
所以 ,
所以 .
故答案为:
13.【答案】 垂直
【解析】 ,
则 平面 平面
所以
故 和 的关系是垂直
14.【答案】 或
【解析】若① ,② ,③ 成立,则 与 可能平行也可能相交,也可能 ,即④ 不一定成立;若① ,② ,④ 成立,则 与 可能平行也可能相交,也可能 ,即③ 不一定成立;若① ,③ ,④ 成立,则② 成立;若② ,③ ,④ 成立,则① 成立,故答案为 或 .
15.【答案】
【解析】由圆 方可知其圆心坐标为 ,半径 ,弦心距 ,∴ ,故答案为 .
16.【答案】 24π或8π
【解析】设圆锥 的外接球球心为 ,则 在直线 上,
设球 的半径为 ,则 ,解得 .
由勾股定理得 ,即 ,可得 ,
即 ,解得 或 .
当 时,圆锥 的体积为 ;
当 时,圆锥 的体积为 .
故答案为:24π或8π.
17.【答案】
【解析】如图所示,
因为平面 平面ABD,所以 平面BDC, 平面ABD,
可得 , ,
取AC的中点O,则 ,
于是外接球的球心是O, ,则 ,
又由 ,
所以半径 ,
所以外接球的体积为 .
故答案为:
18.【答案】
【解析】解:由扇形的面积公式 有: ,解得 ,
由弧长公式有 ,即 ,即该圆锥的母线长为 ,底面圆周长为 ,
即底面圆半径为3,由勾股定理可得圆锥的高为 ,
由圆锥的体积公式可得 ,
故答案为: .
19.【答案】 26;
【解析】结合图形的对称性数一数即可得到面的个数为26个。
根据题意补全该半正多面体的正方体,其俯视图为,
设该半正多面体的棱长为a,则有正方体的棱
长为 , ∴ .
20.【答案】
【解析】如图:
由于 是等边三角形,所以到A,B,D三点距离相等的点在重心O且垂直是平面ABD的直线上,又因为 ,所以到B,C,D三点距离相等的点在过BD中点E且与平面BCD垂直的直线上,两直线的交点是O,所以球心为O.半径R= , 。填 。
三、解答题
21.【答案】 解:圆C: 直角坐标方程为 ,即
直线 : 的直角坐标方程为
圆心 到直线 的距离
所以 ,
22.【答案】 (1)解:∵圆心 在 轴上且该圆与 轴相切,
∴设圆心 ,半径 , ,
设圆的方程为 ,将点 代入得 ,
∴ ,
∴所求圆C的方程为 .
(2)解:∵圆心 到直线 : 的距离
,
∴直线 被圆截得的弦长为 .
23.【答案】 (1)设 与 相交于点 ,则 为 中点,连接 ,
∵ 为 中点,∴ ,
又∵ 平面 ,∴ 平面 ;
(2)连接 ,则 ,
在正三棱柱 中, 平面 ,
则 与 到平面 的距离相等,
∵ 为 的中点,∴ ,
又平面 平面 ,且平面 平面 ,
∴ 平面 ,
在等边三角形 中,由 ,得 ,
又正三棱柱的侧棱长为 ,∴ ,
∴ .
24.【答案】 解:(I) ,
,
(II)
, , ,
综合复习与测试
一、单选题
1.(2020高二上·遵义月考)若直线经过 两点,则直线 的倾斜角为( )
A. 30 B. 45 C. 60 D. 120
2.(2019高二下·青浦期末)已知空间不重合的三条直线l、m、n及一个平面 ,下列命题中的假命题是( ).
A. 若 , ,则 B. 若 , ,则
C. 若 , ,则 D. 若 , ,则
3.(2020高三上·宁波期末)如图,正方体 中, ,点 在侧面 内.若 ,则点 的轨迹为( )
A. 线段 B. 圆弧 C. 抛物线一部分 D. 椭圆一部分
4.(2019高一下·韶关期末)如图是正方体的展开图,则在这个正方体中:
① 与 平行;② 与 是异面直线;③ 与 成60°角;④ 与 垂直.以上四个命题中,正确命题的序号是( )
A. ①②③ B. ②④ C. ③④ D. ②③④
5.(2019高一下·韶关期末)已知直线 与圆 交于A、B两点,O是坐标原点,向量 、 满足 ,则实数a的值是( )
A. 2 B. -2 C. 或 D. 2或-2
6.(2019·云南模拟)已知直三棱柱 的顶点都在球 的球面上, , ,若球 的表面积为 ,则这个直三棱柱的体积是( )
A. 16 B. 15 C. D.
7.(2020高二上·朝阳期末)如图,将边长为4的正方形折成一个正四棱柱的侧面,则异面直线AK和LM所成角的大小为( )
A. 30° B. 45° C. 60° D. 90°
8.(2021高三上·河南月考)我国南北朝时期的数学家祖暅提出了一个原理“幂势既同,则积不容异”,即夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.现有某几何体和一个圆锥满足祖暅原理的条件,若该圆锥的侧面展开图是半径为2的一个半圆,则该几何体的体积为( )
A. B. C. D.
9.(2020·江西模拟)在平面五边形 中, , , , ,且 .将五边形 沿对角线 折起,使平面 与平面 所成的二面角为 ,则沿对角线 折起后所得几何体的外接球的表面积为( )
A. B. C. D.
10.(2019高三上·广东月考)已知三棱锥 的四个顶点在球 的球面上,点 分别是 的中点, ,则球 的表面积为( )
A. B. C. D.
11.(2019高三上·柳州月考)已知三棱锥 的四个顶点均在球 的球面上, 和 所在平面互相垂直, , , ,则球 的体积为( )
A. B. C. D.
二、填空题
12.点 关于直线 的对称点是 , 关于原点O的对称点是 ,则 ________.
13.(2020高二上·重庆月考)已知△ABC和直线l,若l⊥AB,l⊥BC,则l和AC的关系是________.
14.(2020高二上·四川月考)α、β是两个不同的平面,m、n是平面α及β之外的两条不同直线,
给出四个论断:
① m ^ n ②α^β ③ m ^β ④ n ^α
以其中三个论断作为条件,余下一个论断作为结论,写出你认为
正确的一个命题:________.
15.(2020高二上·成都月考)已知直线 和圆 相交于 、 两点,则弦长 ________.
16.(2021·衡阳模拟)设圆锥的顶点为 , 为圆锥底面圆 的直径,点 为圆 上的一点(异于 、 ),若 ,三棱锥 的外接球表面积为 ,则圆锥的体积为 .
17.(2020高二上·安徽期中)在平行四边形ABCD中, , ,将此平行四边形沿对角线BD折叠,使平面 平面CBD,则三棱锥A-BCD外接球的体积是________.
18.(2019高三上·杨浦期中)已知圆锥的侧面展开图是一个扇形,若此扇形的圆心角为 、面积为 ,则该圆锥的体积为 .
19.(2019·全国Ⅱ卷理)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为________.
20.(2020高三上·兴宁期末)已知空间四边形 中, , , ,若平面 平面 ,则该几何体的外接球表面积为________.
三、解答题
21.(2020·盐城模拟)在极坐标系中,已知圆 和直线 相交于 两点,求线段 的长.
22.(2019高一下·广东期末)已知直线 : ,过点 且圆心在x轴上的圆C与y轴相切.
(1)求圆C的方程;
(2)求直线l被圆C截得的弦长.
23.(2021高一下·长春期末)如图,正三棱柱 的底面边长是2,侧棱长是 , 是 的中点.
(1)求证: 平面 ;
(2)求三棱锥 的体积.
24.(2019高一下·石河子月考)如图,
(I)求证
(II)设
答案解析部分
一、单选题
1.【答案】 A
【解析】设直线AB的倾斜角为 ,由两点斜率公式的直线AB的斜率 所以 ,
故答案为:A.
2.【答案】 B
【解析】对于A选项,根据平行公理可知,A选项正确.
对于B选项,两条直线平行与同一个平面,这两条直线可以相交、平行或异面,B选项是假命题.
对于C选项,由于 , ,根据空间角的定义可知, ,C选项正确.
对于D选项,由于 ,所以 平行于平面 内一条直线 ,而 ,所以 ,所以 ,即D选项正确.
故答案为:B.
3.【答案】 A
【解析】如图建立空间直角坐标系,
设棱长为3, , , , , , ,
,整理为: ,
所以点 的轨迹方程是关于 的二元一次方程,所以点M的轨迹是平面 平面内,直线 内的一段线段。
故答案为:A
4.【答案】 C
【解析】将正方体的展开图还原为正方体ABCD﹣EFMN后,
可得AF,CN异面;BM,AN平行;
连接AN,NF,可得∠FAN为AF,BM所成角,且为60°;
BN⊥DE,DE⊥AB可得DE⊥平面ABN,可得DE⊥BN,
可得③④正确,
故答案为:C.
5.【答案】 D
【解析】由 ,两边平方,得 ,
所以 ,则 为等腰直角三角形,
而圆 的半径AO=2,
则原点O到直线x+y=a的距离为 ,
所以 ,解得a的值为2或-2。
故答案为:D.
6.【答案】 A
【解析】由题, ,
因为 , ,易知三角形ABC为等腰直角三角形,
故三棱柱的高
故体积
故答案为:A
7.【答案】 D
【解析】由题知,折叠后的正四棱锥如图所示,
易知K为 的四等分点,L为 的中点,M为 的四等分点, ,
取 的中点N,易证 ,
则异面直线AK和LM所成角即直线AK和KN所成角 ,
在 中, , ,
故
故答案为:D
8.【答案】 C
【解析】圆锥底面周长为 ,
所以圆锥的底面半径 ,圆锥的高 ,
所以圆锥的体积为 ,
由祖暅原理,该几何体的体积也为 .
故答案为:C
9.【答案】 C
【解析】设 的中心为 ,矩形 的中心为 ,
过 作垂直于平面 的直线 ,
过 作垂直于平面 的直线 ,
则由球的性质可知,直线 与 的交点 ,
即几何体 外接球的球心..取 的中点 ,
连接 , ,由条件得 ,
.连接 ,因为 ,
从而 .连接 ,则 为所得几何体外接球的半径.
又 ,则 ,
故所得几何体外接球的表面积等于 .
故答案为:C.
10.【答案】 C
【解析】
,
平面 平面 ,
点 分别是 的中点, ,
设球 半径为
,
故答案为:C
11.【答案】 D
【解析】解:
, , ,
,
,
的外接圆的半径为
和 所在平面互相垂直,
球心在 边的高上,
设球心到平面 的距离为 ,
则
,
球 体积 .
故答案为:D
二、填空题
12.【答案】
【解析】因为点 关于直线 的对称点是
所以 ,
又因为 关于原点O的对称点是
所以 ,
所以 .
故答案为:
13.【答案】 垂直
【解析】 ,
则 平面 平面
所以
故 和 的关系是垂直
14.【答案】 或
【解析】若① ,② ,③ 成立,则 与 可能平行也可能相交,也可能 ,即④ 不一定成立;若① ,② ,④ 成立,则 与 可能平行也可能相交,也可能 ,即③ 不一定成立;若① ,③ ,④ 成立,则② 成立;若② ,③ ,④ 成立,则① 成立,故答案为 或 .
15.【答案】
【解析】由圆 方可知其圆心坐标为 ,半径 ,弦心距 ,∴ ,故答案为 .
16.【答案】 24π或8π
【解析】设圆锥 的外接球球心为 ,则 在直线 上,
设球 的半径为 ,则 ,解得 .
由勾股定理得 ,即 ,可得 ,
即 ,解得 或 .
当 时,圆锥 的体积为 ;
当 时,圆锥 的体积为 .
故答案为:24π或8π.
17.【答案】
【解析】如图所示,
因为平面 平面ABD,所以 平面BDC, 平面ABD,
可得 , ,
取AC的中点O,则 ,
于是外接球的球心是O, ,则 ,
又由 ,
所以半径 ,
所以外接球的体积为 .
故答案为:
18.【答案】
【解析】解:由扇形的面积公式 有: ,解得 ,
由弧长公式有 ,即 ,即该圆锥的母线长为 ,底面圆周长为 ,
即底面圆半径为3,由勾股定理可得圆锥的高为 ,
由圆锥的体积公式可得 ,
故答案为: .
19.【答案】 26;
【解析】结合图形的对称性数一数即可得到面的个数为26个。
根据题意补全该半正多面体的正方体,其俯视图为,
设该半正多面体的棱长为a,则有正方体的棱
长为 , ∴ .
20.【答案】
【解析】如图:
由于 是等边三角形,所以到A,B,D三点距离相等的点在重心O且垂直是平面ABD的直线上,又因为 ,所以到B,C,D三点距离相等的点在过BD中点E且与平面BCD垂直的直线上,两直线的交点是O,所以球心为O.半径R= , 。填 。
三、解答题
21.【答案】 解:圆C: 直角坐标方程为 ,即
直线 : 的直角坐标方程为
圆心 到直线 的距离
所以 ,
22.【答案】 (1)解:∵圆心 在 轴上且该圆与 轴相切,
∴设圆心 ,半径 , ,
设圆的方程为 ,将点 代入得 ,
∴ ,
∴所求圆C的方程为 .
(2)解:∵圆心 到直线 : 的距离
,
∴直线 被圆截得的弦长为 .
23.【答案】 (1)设 与 相交于点 ,则 为 中点,连接 ,
∵ 为 中点,∴ ,
又∵ 平面 ,∴ 平面 ;
(2)连接 ,则 ,
在正三棱柱 中, 平面 ,
则 与 到平面 的距离相等,
∵ 为 的中点,∴ ,
又平面 平面 ,且平面 平面 ,
∴ 平面 ,
在等边三角形 中,由 ,得 ,
又正三棱柱的侧棱长为 ,∴ ,
∴ .
24.【答案】 解:(I) ,
,
(II)
, , ,
