人教新课标A版必修5 综合复习与测试 (含答案)
文档属性
| 名称 | 人教新课标A版必修5 综合复习与测试 (含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 66.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 15:06:38 | ||
图片预览



文档简介
人教新课标A版必修5
综合复习与测试
一、单选题
1.(2021高二上·子洲开学考)已知圆 ,若圆 刚好被直线 平分,则 的最小值为( )
A. B. C.18 D.
2.(2020高二下·成都期中)直线 过抛物线 的焦点 且与抛物线交于 , 两点,若线段 的长分别为 ,则 的最小值是( )
A. 10 B. 9 C. 8 D. 7
3.(2019高一下·上杭期中)若点 都在函数 图象上,则数列 的前n项和最小时的n等于( )
A. 7或8 B. 7 C. 8 D. 8或9
4.(2019高一下·鹤岗月考)已知 , 都为正实数, ,则 的最大值是( )
A. B. C. D.
5.(2019高二上·湖南月考)已知正数a,b满足a+b=3.则 的最小值为( )
A. B. C. D.
6.(2019高二上·邵阳期中)设变量 满足约束条件 ,则目标函数 的最小值为( )
A. B. C. D.
7.(2019高一下·重庆期中)已知数列 满足: , ,则 ( )
A. B. C. D.
8.(2019高一下·安徽月考)对于数列 ,若任意 ,都有 ( 为常数)成立,则称数列 满足 级收敛,若数列 的通项公式为 ,且满足 级收敛,则 的最大值为( )
A. 6 B. 3 C. 2 D. 0
9.(2021·日照模拟)在棱长为 的正方体 中,球 同时与以 为公共顶点的三个面相切,球 同时与以 为公共顶点的三个面相切,且两球相切于点 ,若球 , 的半径分别为 , ,则( )
A.
B.
C. 这两个球的体积之和的最小值是
D. 这两个球的表面积之和的最小值是
10.(2021高三上·南溪月考)已知函数 , , ,则 的最小值等于( )
A. B. C. D.
二、填空题
11.(2020高一下·长春期中)记等差数列 的前n项和为 ,已知 , ,则 ________.
12.(2020高一上·丰台期中)函数 的最小值是________,此时 ________.
13.(2020高二上·大荔期末)已知正数 满足 ,则 的最小值为________.
14.(2020·宝山模拟)已知 、 均是等差数列, ,若 前三项是7、9、9,则 ________
15.(2020高一上·东丽期末)设 , 在 ________时y的最小值等于________.
16.(2020高二上·天津月考)若直线 始终平分圆 的周长,则 的最小值为________.
17.(2019高一上·静海月考)若 , , ,则 的最小值为________.
18.(2019高三上·吉林月考)直线 ( , )过圆 : 的圆心,则 的最小值是________.
19.(2019高三上·深圳期末)等差数列 的前n项和为 , , , 对一切 恒成立,则 的取值范围为________.
20.(2021·义乌模拟)已知数列 ,则数列 的前 项和 .
三、解答题
21.(2020高二上·常熟期中)已知关于x的不等式 的解集为空集,函数 在 上的值域为B.
(1)求实数a的取值集合A及函数 的值域B;
(2)对(1)中的集合A,B,若 是 的必要不充分条件,求实数m的取值范围.
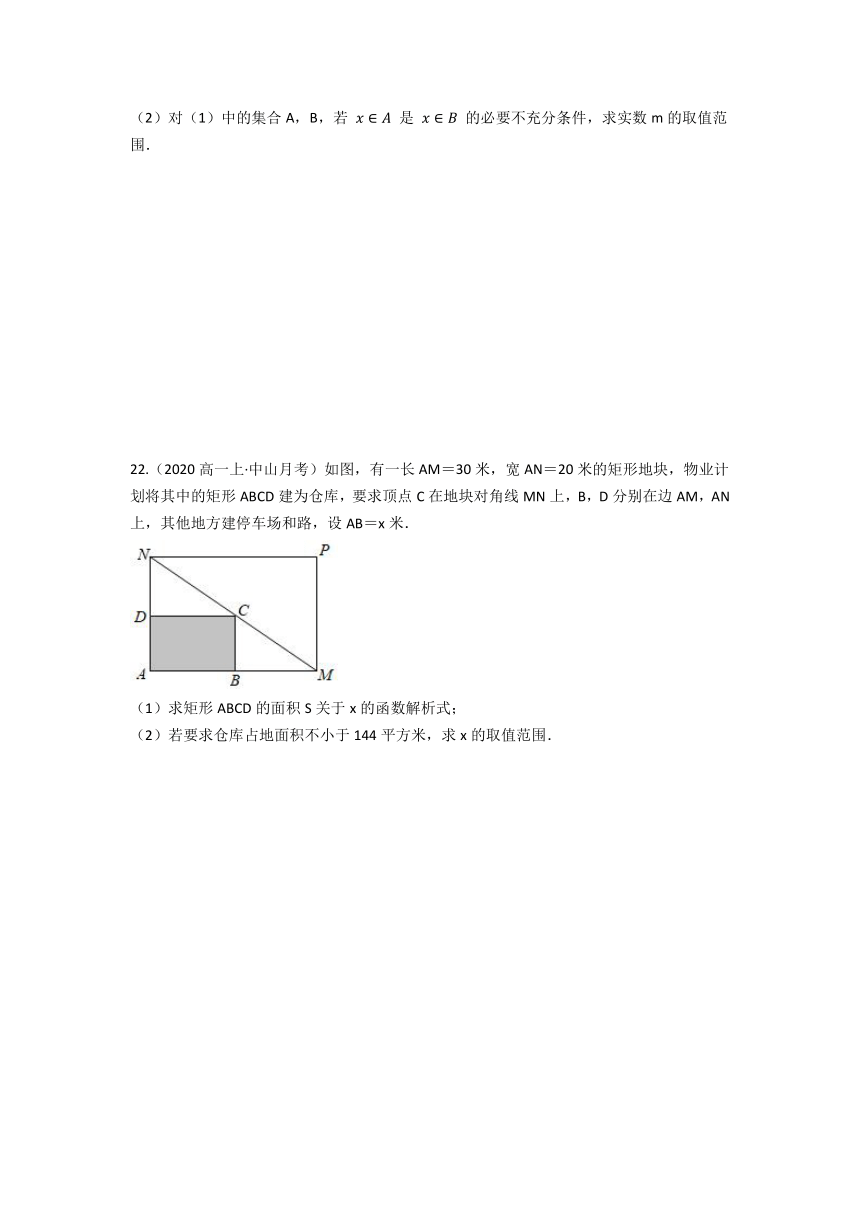
22.(2020高一上·中山月考)如图,有一长AM=30米,宽AN=20米的矩形地块,物业计划将其中的矩形ABCD建为仓库,要求顶点C在地块对角线MN上,B,D分别在边AM,AN上,其他地方建停车场和路,设AB=x米.
(1)求矩形ABCD的面积S关于x的函数解析式;
(2)若要求仓库占地面积不小于144平方米,求x的取值范围.
23.(2020高三上·海口月考)已知函数 ,( , , )的最小正周期为 .
(1)从① ;② ;③ ,都有 这三个条件中,选择合适的两个条件,求函数 的解析式;
(2)求(1)中所求得的函数 在区间 上的最大值和最小值.
24.(2019高二上·山西月考)已知 是递增数列,其前 项和为 , ,且 , .
(Ⅰ)求数列 的通项 ;
(Ⅱ)是否存在 使得 成立?若存在,写出一组符合条件的 的值;若不存在,请说明理由;
(Ⅲ)设 ,若对于任意的 ,不等式
恒成立,求正整数 的最大值.
答案解析部分
一、单选题
1.【答案】 C
【解析】根据题意,有圆心在直线上,所以有 ,
所以有 ,
故答案为:C.
2.【答案】 B
【解析】抛物线的焦点为 ,准线为 ,如图,过 作 于 ,过 作 于 ,过 作 于 ,交 轴于 点,准线 与 轴交于点 ,
则 , , ,
∴ , ,
由 得 ,∴ ,
∴ ,当且仅当 ,即 时等号成立.
故答案为:B.
3.【答案】 A
【解析】由题得 ,则 的前n项 = ,对称轴为x= ,故 的前n项和最小时的n等于7或8
故答案为:A
4.【答案】 B
【解析】因为 , 都为正实数, ,
所以 ,
当且仅当 ,即 时, 取最大值 .
故答案为:B
5.【答案】 A
【解析】依题意 ,所以 ,当且仅当 等号成立.
故答案为:A.
6.【答案】 A
【解析】画出变量 满足的可行域(见下图阴影部分),
目标函数 可化为 ,显然直线 在 轴上的截距最小时, 最小,
平移直线 经过点 时, 最小,
联立 ,解得 ,此时 .
故答案为:A.
7.【答案】 B
【解析】数列 满足: , ,
是以 为首项 为公差的等差数列,
故答案为:B.
8.【答案】 D
【解析】由题意: 对任意的 恒成立, ,且 级收敛,则 恒成立,即 恒成立,据此可知数列 是递增数列或常数列,令 ,根据数列是单调递增的得到
据此可得: 恒成立,故 , 的最大值为0.
故答案为:D.
9.【答案】 C
【解析】球 同时与以 为公共顶点的三个面相切,以 为对角线可构造一个正方体,边长为 , 所以 ,同理
,
则 ,
所以 ,
故这两个球的体积之和为: ,
因为 ,所以 ,
即 ,当且仅当 时等号成立,
这两个球的表面积之和 ,
当且仅当 时等号成立,
A,B,D项均错误.
故答案为:C.
10.【答案】 B
【解析】解:∵ , , ,
∴lgm=-lgn
∴ , 即mn=1
∴
当且仅当时,等号成立
则 的最小值为
故答案为:B
二、填空题
11.【答案】 36
【解析】由 , ,
则 ,解得 , ,
所以 .
故答案为:36
12.【答案】 3;2
【解析】∵ ,
∴ ,
由基本不等式可得 ,
当且仅当 即 时,函数取得最小值 .
故答案为:①3;②2.
13.【答案】 9
【解析】因为正数 满足 ,
所以 ,即 ,
所以 ,
当且仅当 ,即 , 时,等号成立.
故答案为:9
14.【答案】 -47
【解析】解:因为 、 均是等差数列,其通项公式均为关于 的一次式,所以 为关于 的二次式,
故设 ,
, ,
则 ,解得
,
故答案为: .
15.【答案】 2;3
【解析】因为 ,所以 ,
,
当且仅当 即 时等号成立,
所以在 时y的最小值等于 ,
故答案为:2;3 。
16.【答案】
【解析】由题意 ,
所以 ,
当且仅当 时等号成立.
17.【答案】 7
【解析】 =
当且仅当 时,等号成立.
18.【答案】
【解析】圆 : 的标准方程为 ,圆心为 ,
由题意 ,即 ,
∴ ,当且仅当 ,即 时等号成立,
故答案为: .
19.【答案】
【解析】 , ,
所以 , ,
, ,
由 得 ,
由函数 的单调性及 知,
当 或 时, 最小值为30,故 .
20.【答案】
【解析】设数列 的前 项和为 ,
当 , ,解得: ,
当 时, ,当 ,
当 时, ,
当 时, ,
所以 .
故答案为:
三、解答题
21.【答案】 (1)1°若 ,则 不符合;
2°若 ,则 ,则 或 ,∴ ;
3°若 不成立;
综上, ,∴ .
令 ,则 .
∴ .
当且仅当 即 时等号成立,此时 .
∴ .
(2)∵ 是 的必要不充分条件,
∴B是A的真子集,则 ,解得 .
22.【答案】 (1)∵△NDC∽△NAM,∴ ,即 ,∴ ,
∴ ,
(2)根据题意,得 ,即 ,
解得 ,所以 的取值范围是 .
23.【答案】 (1)解:因为 的最小正周期为 ,
所以 ,解得 .
选①②:
因为 ,所以 ,
解得 , .
因为 ,所以 .
又因为 ,
所以 ,即 ,
所以 .
所以 .
选②③:
因为 ,都有 ,
所以 时, 取得最大值,即 ,
所以 , ,
所以 ,所以 .
又因为 ,
所以 ,即 ,
所以 .
所以
(2)解:因为 ,
所以 ,
所以 ,
当 时, 取得最小值为-1;
当 时, 取得最大值为 ;
所以 取得最小值为-1,最大值为 .
24.【答案】 解:(Ⅰ) ,得 ,解得 ,或 .
由于 ,所以 .
因为 ,所以 .
故 ,
整理,得 ,即 .
因为 是递增数列,且 ,故 ,因此 .
则数列 是以2为首项, 为公差的等差数列.
所以
(Ⅱ)满足条件的正整数 不存在,证明如下:
假设存在 ,使得 ,
则 .
整理,得 , ①
显然,左边为整数,所以①式不成立.
故满足条件的正整数 不存在.
(Ⅲ) ,
不等式 可转化为
.
设 ,
则
.
所以 ,即当 增大时, 也增大.
要使不等式 对于任意的 恒成立,只需 即可.
因为 ,所以 .
即 .
所以,正整数 的最大值为8.
综合复习与测试
一、单选题
1.(2021高二上·子洲开学考)已知圆 ,若圆 刚好被直线 平分,则 的最小值为( )
A. B. C.18 D.
2.(2020高二下·成都期中)直线 过抛物线 的焦点 且与抛物线交于 , 两点,若线段 的长分别为 ,则 的最小值是( )
A. 10 B. 9 C. 8 D. 7
3.(2019高一下·上杭期中)若点 都在函数 图象上,则数列 的前n项和最小时的n等于( )
A. 7或8 B. 7 C. 8 D. 8或9
4.(2019高一下·鹤岗月考)已知 , 都为正实数, ,则 的最大值是( )
A. B. C. D.
5.(2019高二上·湖南月考)已知正数a,b满足a+b=3.则 的最小值为( )
A. B. C. D.
6.(2019高二上·邵阳期中)设变量 满足约束条件 ,则目标函数 的最小值为( )
A. B. C. D.
7.(2019高一下·重庆期中)已知数列 满足: , ,则 ( )
A. B. C. D.
8.(2019高一下·安徽月考)对于数列 ,若任意 ,都有 ( 为常数)成立,则称数列 满足 级收敛,若数列 的通项公式为 ,且满足 级收敛,则 的最大值为( )
A. 6 B. 3 C. 2 D. 0
9.(2021·日照模拟)在棱长为 的正方体 中,球 同时与以 为公共顶点的三个面相切,球 同时与以 为公共顶点的三个面相切,且两球相切于点 ,若球 , 的半径分别为 , ,则( )
A.
B.
C. 这两个球的体积之和的最小值是
D. 这两个球的表面积之和的最小值是
10.(2021高三上·南溪月考)已知函数 , , ,则 的最小值等于( )
A. B. C. D.
二、填空题
11.(2020高一下·长春期中)记等差数列 的前n项和为 ,已知 , ,则 ________.
12.(2020高一上·丰台期中)函数 的最小值是________,此时 ________.
13.(2020高二上·大荔期末)已知正数 满足 ,则 的最小值为________.
14.(2020·宝山模拟)已知 、 均是等差数列, ,若 前三项是7、9、9,则 ________
15.(2020高一上·东丽期末)设 , 在 ________时y的最小值等于________.
16.(2020高二上·天津月考)若直线 始终平分圆 的周长,则 的最小值为________.
17.(2019高一上·静海月考)若 , , ,则 的最小值为________.
18.(2019高三上·吉林月考)直线 ( , )过圆 : 的圆心,则 的最小值是________.
19.(2019高三上·深圳期末)等差数列 的前n项和为 , , , 对一切 恒成立,则 的取值范围为________.
20.(2021·义乌模拟)已知数列 ,则数列 的前 项和 .
三、解答题
21.(2020高二上·常熟期中)已知关于x的不等式 的解集为空集,函数 在 上的值域为B.
(1)求实数a的取值集合A及函数 的值域B;
(2)对(1)中的集合A,B,若 是 的必要不充分条件,求实数m的取值范围.
22.(2020高一上·中山月考)如图,有一长AM=30米,宽AN=20米的矩形地块,物业计划将其中的矩形ABCD建为仓库,要求顶点C在地块对角线MN上,B,D分别在边AM,AN上,其他地方建停车场和路,设AB=x米.
(1)求矩形ABCD的面积S关于x的函数解析式;
(2)若要求仓库占地面积不小于144平方米,求x的取值范围.
23.(2020高三上·海口月考)已知函数 ,( , , )的最小正周期为 .
(1)从① ;② ;③ ,都有 这三个条件中,选择合适的两个条件,求函数 的解析式;
(2)求(1)中所求得的函数 在区间 上的最大值和最小值.
24.(2019高二上·山西月考)已知 是递增数列,其前 项和为 , ,且 , .
(Ⅰ)求数列 的通项 ;
(Ⅱ)是否存在 使得 成立?若存在,写出一组符合条件的 的值;若不存在,请说明理由;
(Ⅲ)设 ,若对于任意的 ,不等式
恒成立,求正整数 的最大值.
答案解析部分
一、单选题
1.【答案】 C
【解析】根据题意,有圆心在直线上,所以有 ,
所以有 ,
故答案为:C.
2.【答案】 B
【解析】抛物线的焦点为 ,准线为 ,如图,过 作 于 ,过 作 于 ,过 作 于 ,交 轴于 点,准线 与 轴交于点 ,
则 , , ,
∴ , ,
由 得 ,∴ ,
∴ ,当且仅当 ,即 时等号成立.
故答案为:B.
3.【答案】 A
【解析】由题得 ,则 的前n项 = ,对称轴为x= ,故 的前n项和最小时的n等于7或8
故答案为:A
4.【答案】 B
【解析】因为 , 都为正实数, ,
所以 ,
当且仅当 ,即 时, 取最大值 .
故答案为:B
5.【答案】 A
【解析】依题意 ,所以 ,当且仅当 等号成立.
故答案为:A.
6.【答案】 A
【解析】画出变量 满足的可行域(见下图阴影部分),
目标函数 可化为 ,显然直线 在 轴上的截距最小时, 最小,
平移直线 经过点 时, 最小,
联立 ,解得 ,此时 .
故答案为:A.
7.【答案】 B
【解析】数列 满足: , ,
是以 为首项 为公差的等差数列,
故答案为:B.
8.【答案】 D
【解析】由题意: 对任意的 恒成立, ,且 级收敛,则 恒成立,即 恒成立,据此可知数列 是递增数列或常数列,令 ,根据数列是单调递增的得到
据此可得: 恒成立,故 , 的最大值为0.
故答案为:D.
9.【答案】 C
【解析】球 同时与以 为公共顶点的三个面相切,以 为对角线可构造一个正方体,边长为 , 所以 ,同理
,
则 ,
所以 ,
故这两个球的体积之和为: ,
因为 ,所以 ,
即 ,当且仅当 时等号成立,
这两个球的表面积之和 ,
当且仅当 时等号成立,
A,B,D项均错误.
故答案为:C.
10.【答案】 B
【解析】解:∵ , , ,
∴lgm=-lgn
∴ , 即mn=1
∴
当且仅当时,等号成立
则 的最小值为
故答案为:B
二、填空题
11.【答案】 36
【解析】由 , ,
则 ,解得 , ,
所以 .
故答案为:36
12.【答案】 3;2
【解析】∵ ,
∴ ,
由基本不等式可得 ,
当且仅当 即 时,函数取得最小值 .
故答案为:①3;②2.
13.【答案】 9
【解析】因为正数 满足 ,
所以 ,即 ,
所以 ,
当且仅当 ,即 , 时,等号成立.
故答案为:9
14.【答案】 -47
【解析】解:因为 、 均是等差数列,其通项公式均为关于 的一次式,所以 为关于 的二次式,
故设 ,
, ,
则 ,解得
,
故答案为: .
15.【答案】 2;3
【解析】因为 ,所以 ,
,
当且仅当 即 时等号成立,
所以在 时y的最小值等于 ,
故答案为:2;3 。
16.【答案】
【解析】由题意 ,
所以 ,
当且仅当 时等号成立.
17.【答案】 7
【解析】 =
当且仅当 时,等号成立.
18.【答案】
【解析】圆 : 的标准方程为 ,圆心为 ,
由题意 ,即 ,
∴ ,当且仅当 ,即 时等号成立,
故答案为: .
19.【答案】
【解析】 , ,
所以 , ,
, ,
由 得 ,
由函数 的单调性及 知,
当 或 时, 最小值为30,故 .
20.【答案】
【解析】设数列 的前 项和为 ,
当 , ,解得: ,
当 时, ,当 ,
当 时, ,
当 时, ,
所以 .
故答案为:
三、解答题
21.【答案】 (1)1°若 ,则 不符合;
2°若 ,则 ,则 或 ,∴ ;
3°若 不成立;
综上, ,∴ .
令 ,则 .
∴ .
当且仅当 即 时等号成立,此时 .
∴ .
(2)∵ 是 的必要不充分条件,
∴B是A的真子集,则 ,解得 .
22.【答案】 (1)∵△NDC∽△NAM,∴ ,即 ,∴ ,
∴ ,
(2)根据题意,得 ,即 ,
解得 ,所以 的取值范围是 .
23.【答案】 (1)解:因为 的最小正周期为 ,
所以 ,解得 .
选①②:
因为 ,所以 ,
解得 , .
因为 ,所以 .
又因为 ,
所以 ,即 ,
所以 .
所以 .
选②③:
因为 ,都有 ,
所以 时, 取得最大值,即 ,
所以 , ,
所以 ,所以 .
又因为 ,
所以 ,即 ,
所以 .
所以
(2)解:因为 ,
所以 ,
所以 ,
当 时, 取得最小值为-1;
当 时, 取得最大值为 ;
所以 取得最小值为-1,最大值为 .
24.【答案】 解:(Ⅰ) ,得 ,解得 ,或 .
由于 ,所以 .
因为 ,所以 .
故 ,
整理,得 ,即 .
因为 是递增数列,且 ,故 ,因此 .
则数列 是以2为首项, 为公差的等差数列.
所以
(Ⅱ)满足条件的正整数 不存在,证明如下:
假设存在 ,使得 ,
则 .
整理,得 , ①
显然,左边为整数,所以①式不成立.
故满足条件的正整数 不存在.
(Ⅲ) ,
不等式 可转化为
.
设 ,
则
.
所以 ,即当 增大时, 也增大.
要使不等式 对于任意的 恒成立,只需 即可.
因为 ,所以 .
即 .
所以,正整数 的最大值为8.
