北师大版八年级数学上册 4.3 一次函数的图像和性质(1)课件(共19张PPT)
文档属性
| 名称 | 北师大版八年级数学上册 4.3 一次函数的图像和性质(1)课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 20:52:10 | ||
图片预览





文档简介
(共19张PPT)
一次函数的图像和性质
x
y
0
提问复习,引入新课
1、什么叫正比例函数、一次函数?它们之间有什么关系?
2、正比例函数的图象是什么形状?
一般地,形如 的函数,叫做正比例函数;
一般地,形如 的函数,叫做一次函数。
当b=0时,y=kx+b就变成了 ,所以说正比例函数是一种特殊的一次函数。
正比例函数的图象是( )
y=kx(k是常数,k≠0)
y=kx+b(k,b是常数,k≠0)
y=kx
经过原点的一条直线
y=kx
图 象 性 质
K>0 y
x
K<0
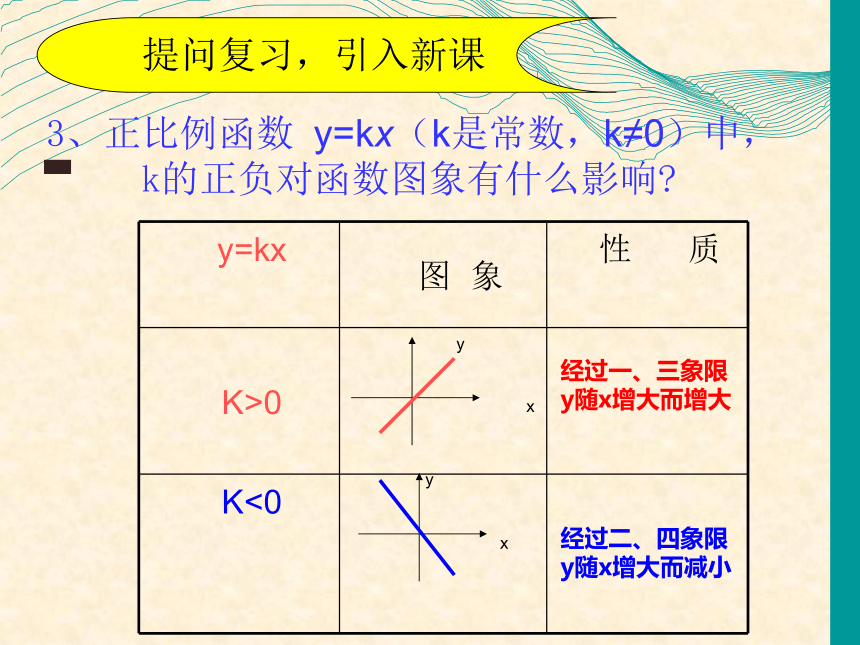
经过一、三象限
y随x增大而增大
经过二、四象限
y随x增大而减小
3、正比例函数 y=kx(k是常数,k≠0)中,
k的正负对函数图象有什么影响
提问复习,引入新课
y
x
既然正比例函数是特殊的一次函数,正比例函数的图象是直线,那么一次函数的图象也会是一条直线吗? 它们图象之间有什么关系 一次函数又有什么性质呢
提问复习,引入新课
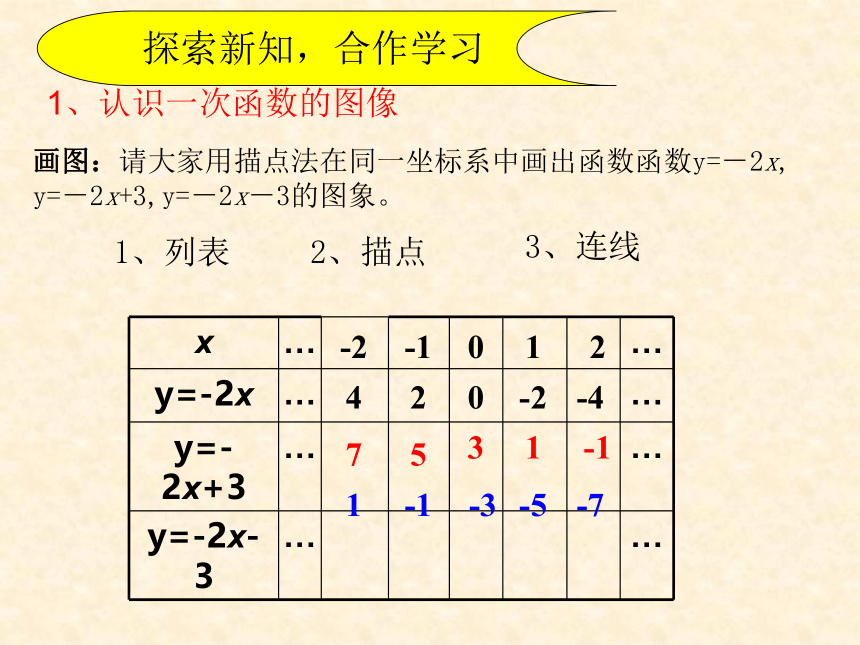
画图:请大家用描点法在同一坐标系中画出函数函数y=-2x, y=-2x+3,y=-2x-3的图象。
1、列表
2、描点
3、连线
x … …
y=-2x … …
y=-2x+3 … …
y=-2x-3 … …
4
7
-1
2
5
1
0
3
-3
-2
1
-5
-4
-1
-7
-2
-1
0
2
1
1、认识一次函数的图像
探索新知,合作学习
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y=-2x
y=-2x+3
y=-2x-3
比一比:正比例函数y=-2x与一次函数y=-2x+3 、y=-2x-3图象有什么异同点.
观察:比较上面三个函数的相同点与不同点,根据你的观察结果回答下列问题:
(1)这三个函数的图象形状都是___,并且倾斜程度___;
(2)函数y=-2x图象经过原点,一次函数y=-2x+3 的图象与y轴交于点____,即它可以看作由直线y=-2x向__平移__单位长度而得到;
一次函数y=-2x-3的图象与y轴交于点____,即它可以看作由直线y=-2x向__平移__单位长度而得到;
直线
相同
(0,3)
上
3个
(0,-3)
下
3个
推广:
(1) 所有一次函数y=kx+b的图象都是________
(2)直线 y=kx+b与直线y=kx__________;
(3)直线 y=kx+b可以看作由直线y=kx___________
而得到
一条直线;
互相平行
平移 个单位
当b>0,向上平移b个单位;
当b<0,向下平移b个单位。
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
实践:用两点法在同一坐标系中画出函数y=2x-1
与y=-0.5x+1的图象.
x
y=2x-1
x
y= -0.5x+1
2、用两点法画一次函数图像
总结:
画一次函数的图像时,只要描出合适关系式的两点,再连接两点即可,我们通常选
取(0,b)和(- ,0 )这两个点,也就
是选取图像与x轴和y轴的交点坐标。
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
实践:用两点法在同一坐标系中画出函数y=2x-1
与y=-0.5x+1的图象.
x
y=2x-1
x
y= -0.5x+1
0
0
-1
0
0.5
0
1
2
经过(0,-1)和(0.5,0)两点
经过(0,1)和(2,0)两点
y=2x-1
y=-0.5x+1
2、用两点法画一次函数图像
体验:在同一坐标系中用两点法画出函数
y=x+1,
y=-x+1,
y=2x+1
y=-2x+1的图象.
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y=x+1
y=-x+1
y=2x+1
y=-2x+1
3、学习一次函数性质
6.探究:观察上面四个一次函数的图象,类比正比例函数y=kx中k的正负对图象的影响,表述一次函数的性质.
当K>0时,图象呈上升趋势,y随x增大而增大
当K<0时,图象呈下降趋势,y随x增大而减小
小结:
(1)一次函数的图象
由于一次函数y=kx+b(k,b为常数,k≠0)的图象是一条直线,所以一次函数y=kx+b的图象也称为直线y=kx+b.
由于两点确定一条直线,因此在今后作一次函数图象时,只要描出适合关系式的两点,再连成直线即可,一般选取两个特殊点:直线与y轴的交点(0,b),直线与x轴的交点(-,0).但也不必一定选取这两个特殊点.画正比例函数y=kx的图象时,只要描出点(0,0),(1,k)即可.
(2)一次函数y=kx+b(k,b为常数,k≠0)的性质
(1)k的正负决定直线的倾斜方向;
①k>0时,y的值随x值的增大而增大;
②k﹤O时,y的值随x值的增大而减小.
(2)|k|大小决定直线的倾斜程度,即|k|越大,直线与x轴相交的锐角度数越大(直线陡),|k|越小,直线与x轴相交的锐角度数越小(直线缓);
(3)b的正、负决定直线与y轴交点的位置;
①当b>0时,直线与y轴交于正半轴上;
②当b<0时,直线与y轴交于负半轴上;
③当b=0时,直线经过原点,是正比例函数.
题型
1.已知一次函数y=2x﹣3的大致图象为( )
(2)已知函数y=kx+b的图象如图,则y=2kx+b的图象可能是( )
(3)关于x的一次函数y=kx+k2+1的图象可能正确的是( )
如果实数k,b满足kb<0且不等式kx<b的解集是
那么函数y=kx+b的图象只可能是( )
课后
思考:
一次函数的图像和性质
x
y
0
提问复习,引入新课
1、什么叫正比例函数、一次函数?它们之间有什么关系?
2、正比例函数的图象是什么形状?
一般地,形如 的函数,叫做正比例函数;
一般地,形如 的函数,叫做一次函数。
当b=0时,y=kx+b就变成了 ,所以说正比例函数是一种特殊的一次函数。
正比例函数的图象是( )
y=kx(k是常数,k≠0)
y=kx+b(k,b是常数,k≠0)
y=kx
经过原点的一条直线
y=kx
图 象 性 质
K>0 y
x
K<0
经过一、三象限
y随x增大而增大
经过二、四象限
y随x增大而减小
3、正比例函数 y=kx(k是常数,k≠0)中,
k的正负对函数图象有什么影响
提问复习,引入新课
y
x
既然正比例函数是特殊的一次函数,正比例函数的图象是直线,那么一次函数的图象也会是一条直线吗? 它们图象之间有什么关系 一次函数又有什么性质呢
提问复习,引入新课
画图:请大家用描点法在同一坐标系中画出函数函数y=-2x, y=-2x+3,y=-2x-3的图象。
1、列表
2、描点
3、连线
x … …
y=-2x … …
y=-2x+3 … …
y=-2x-3 … …
4
7
-1
2
5
1
0
3
-3
-2
1
-5
-4
-1
-7
-2
-1
0
2
1
1、认识一次函数的图像
探索新知,合作学习
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y=-2x
y=-2x+3
y=-2x-3
比一比:正比例函数y=-2x与一次函数y=-2x+3 、y=-2x-3图象有什么异同点.
观察:比较上面三个函数的相同点与不同点,根据你的观察结果回答下列问题:
(1)这三个函数的图象形状都是___,并且倾斜程度___;
(2)函数y=-2x图象经过原点,一次函数y=-2x+3 的图象与y轴交于点____,即它可以看作由直线y=-2x向__平移__单位长度而得到;
一次函数y=-2x-3的图象与y轴交于点____,即它可以看作由直线y=-2x向__平移__单位长度而得到;
直线
相同
(0,3)
上
3个
(0,-3)
下
3个
推广:
(1) 所有一次函数y=kx+b的图象都是________
(2)直线 y=kx+b与直线y=kx__________;
(3)直线 y=kx+b可以看作由直线y=kx___________
而得到
一条直线;
互相平行
平移 个单位
当b>0,向上平移b个单位;
当b<0,向下平移b个单位。
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
实践:用两点法在同一坐标系中画出函数y=2x-1
与y=-0.5x+1的图象.
x
y=2x-1
x
y= -0.5x+1
2、用两点法画一次函数图像
总结:
画一次函数的图像时,只要描出合适关系式的两点,再连接两点即可,我们通常选
取(0,b)和(- ,0 )这两个点,也就
是选取图像与x轴和y轴的交点坐标。
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
实践:用两点法在同一坐标系中画出函数y=2x-1
与y=-0.5x+1的图象.
x
y=2x-1
x
y= -0.5x+1
0
0
-1
0
0.5
0
1
2
经过(0,-1)和(0.5,0)两点
经过(0,1)和(2,0)两点
y=2x-1
y=-0.5x+1
2、用两点法画一次函数图像
体验:在同一坐标系中用两点法画出函数
y=x+1,
y=-x+1,
y=2x+1
y=-2x+1的图象.
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y=x+1
y=-x+1
y=2x+1
y=-2x+1
3、学习一次函数性质
6.探究:观察上面四个一次函数的图象,类比正比例函数y=kx中k的正负对图象的影响,表述一次函数的性质.
当K>0时,图象呈上升趋势,y随x增大而增大
当K<0时,图象呈下降趋势,y随x增大而减小
小结:
(1)一次函数的图象
由于一次函数y=kx+b(k,b为常数,k≠0)的图象是一条直线,所以一次函数y=kx+b的图象也称为直线y=kx+b.
由于两点确定一条直线,因此在今后作一次函数图象时,只要描出适合关系式的两点,再连成直线即可,一般选取两个特殊点:直线与y轴的交点(0,b),直线与x轴的交点(-,0).但也不必一定选取这两个特殊点.画正比例函数y=kx的图象时,只要描出点(0,0),(1,k)即可.
(2)一次函数y=kx+b(k,b为常数,k≠0)的性质
(1)k的正负决定直线的倾斜方向;
①k>0时,y的值随x值的增大而增大;
②k﹤O时,y的值随x值的增大而减小.
(2)|k|大小决定直线的倾斜程度,即|k|越大,直线与x轴相交的锐角度数越大(直线陡),|k|越小,直线与x轴相交的锐角度数越小(直线缓);
(3)b的正、负决定直线与y轴交点的位置;
①当b>0时,直线与y轴交于正半轴上;
②当b<0时,直线与y轴交于负半轴上;
③当b=0时,直线经过原点,是正比例函数.
题型
1.已知一次函数y=2x﹣3的大致图象为( )
(2)已知函数y=kx+b的图象如图,则y=2kx+b的图象可能是( )
(3)关于x的一次函数y=kx+k2+1的图象可能正确的是( )
如果实数k,b满足kb<0且不等式kx<b的解集是
那么函数y=kx+b的图象只可能是( )
课后
思考:
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
