2021-2022学年鲁教版(五四制)六年级数学上册3.7探索与表达规律 同步达标测评(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)六年级数学上册3.7探索与表达规律 同步达标测评(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 251.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 13:38:19 | ||
图片预览




文档简介
2021-2022学年鲁教版六年级数学上册《3.7探索与表达规律》同步达标测评(附答案)
一.选择题(共10小题,满分40分)
1.观察下面三行数:
﹣2、4、﹣8、16、﹣32、64、……①
0、6、﹣6、18、﹣30、66、……②
﹣1、2、﹣4、8、﹣16、32、……③
设x、y、z分别为第①②③行的第10个数,则2x﹣y﹣2z的值为( )
A.22001 B.0 C.﹣2 D.2
2.如图各正方形中的四个数字之间都有相同的规律,根据这种规律,m的值是( )
A.74 B.104 C.126 D.144
3.如图所示:下列各三角形中的三个数均有相同的规律,由此规律最后一个三角形中,y的值是( )
A.380 B.382 C.384 D.386
4.若a≠2,则我们把称为a的“友好数”,如3的“友好数”是,﹣2的“友好数”是,已知a1=3,a2是a1的“友好数”,a3是a2的“友好数”,a4是a3的“友好数”,……,依此类推,则a2021=( )
A.3 B.﹣2 C. D.
5.右边是一个按某种规律排列的数阵:根据规律,自然数2021应该排在从上向下数的第m行,是该行中的从左向右数的第n个数,那么m+n的值是( )
A.131 B.130 C.129 D.128
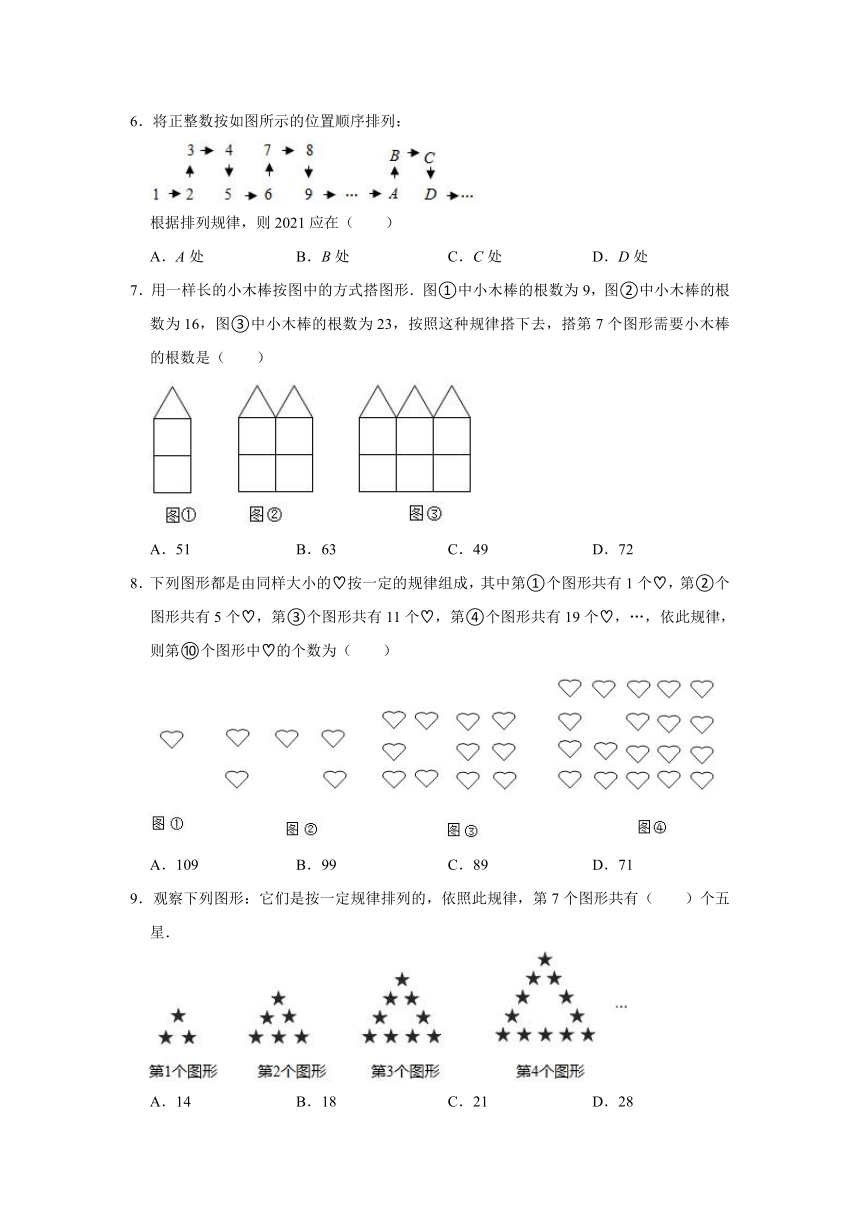
6.将正整数按如图所示的位置顺序排列:
根据排列规律,则2021应在( )
A.A处 B.B处 C.C处 D.D处
7.用一样长的小木棒按图中的方式搭图形.图①中小木棒的根数为9,图②中小木棒的根数为16,图③中小木棒的根数为23,按照这种规律搭下去,搭第7个图形需要小木棒的根数是( )
A.51 B.63 C.49 D.72
8.下列图形都是由同样大小的 按一定的规律组成,其中第①个图形共有1个 ,第②个图形共有5个 ,第③个图形共有11个 ,第④个图形共有19个 ,…,依此规律,则第⑩个图形中 的个数为( )
A.109 B.99 C.89 D.71
9.观察下列图形:它们是按一定规律排列的,依照此规律,第7个图形共有( )个五星.
A.14 B.18 C.21 D.28
10.如图所示,将形状大小完全相同的“ ”按照一定规律摆成下列图形,第1幅图中“ ”的个数为a1,第2幅图中“ ”的个数为a2,第3幅图中“ ”的个数为a3,…,以此类推,的值为( )
A. B. C. D.
二.填空题(共6小题,满分30分)
11.(1+3+5+…+2017+2019+2021)﹣(2+4+6+…+2018+2022)= .
12.观察下面两行数:
﹣2,4,﹣8,16,﹣32,64,…
1,7,﹣5,19,﹣29,67,…
根据你发现的规律,取每行数的第9个数,它们的和等于 .
13.如图所示,在这个数据运算程序中,若开始输入的x值为2,结果输出的是1,返回进行第二次运算则输出的是﹣4,…,则第2021次输出的结果是 .
14.如图图形是由同样大小的棋子按照一定规律排列而成的,其中图①中有5个棋子,图②中有10个棋子,图③中有16个棋子,…,则图中有 个棋子.
15.如图,第一个图形中有1个正方形;第二个图形中有5个正方形;第三个图形中有14个正方形;则按此规律第八个图形有 个正方形.
16.观察下列的“蜂窝图”,则第5个图案中的“六边形”的个数是 ,第n个图案中的“六边形”的个数是 .(用含有n的代数式表示)
三.解答题(共6小题,满分50分)
17.阅读材料,回答问题:求值1+2+22+23+…+22020.
解:设S=1+2+22+23+…+22020.①
将等式两边同时乘2得,2S=2+22+23+…+22020+22021.②
②﹣①得,2S﹣S=22021﹣1,即S=1+2+22+23+…+22020=22021﹣1.
请你仿照此法计算:
(1)1+2+22+23+…+210;
(2)1+3+32+33+…+3n(其中n为正整数).
18.阅读下列材料:
∵=(1﹣),
=(﹣),
=(﹣),
……
=(﹣),
∴+++…+
=(1﹣)+(﹣)+(﹣)+……+(﹣)
=(1﹣+﹣+﹣+……+﹣)
=(1﹣)
=.
解答下列问题:
(1)在+++...中,第6项为 ,第n项是 .
(2)求的值.
19.观察图,解答下列问题.
(1)图中的小圆圈被折线隔开分成六层,第一层有1个小圆圈,第二层有3个圆圈,第三层有5个圆圈,…,第六层有11个圆圈.如果要你继续画下去,第n层有 个小圆圈.
(2)某一层上有65个圆圈,这是第 层.
(3)数图中的圆圈个数可以有多种不同的方法.
比如:前两层的圆圈个数和为(1+3)或22,
由此得,1+3=22.
同样:
由前三层的圆圈个数和得:1+3+5=32.
由前四层的圆圈个数和得:1+3+5+7=42.
…
根据上述规律,从1开始的n个连续奇数之和是多少?用n的代数式把它表示出来 .
(4)运用(3)中的规律计算:73+75+77+…+153.
20.图1为奇数排成的数表,用十字框任意框出5个数,记框内中间这个数为m,其它四个数分别记为a,b,c,d(如图2);图3为按某一规律排成的另一个数表,用十字框任意框出5个数,记框内中间这个数为n,其它四个数记为e,f,g,h(如图4).
(1)请用含m的代数式表示b.
(2)请用含n的代数式表示e.
(3)若a+b+c+d=km,e+f+g+h=pn,求k+3p的值.
21.我国著名数学家华罗庚先生说过:“数形结合百股好,隔裂分家万事休”,数形结合的思想方法在数学中应用极为广泛.
【规律探索】用同样大小的两种不同颜色的正方形纸片,按如图方式拼成长方形:
第(1)个图形中有2张正方形纸片;
第(2)个图形中有2(1+2)=2+4=6张正方形纸片;
第(3)个图形中有2(1+2+3)=2+4+6=12张正方形纸片;
第(4)个图形中有2(1+2+3+4)=2+4+6+8=20张正方形纸片;
…
请你观察上述图形与算式,完成下列问题:
【规律归纳】
(1)第(7)个图形中有 张正方形纸片(直接写出结果);
(2)根据上面的发现我们可以猜想:2+4+6+2n= (用含n的代数式表示);
【规律应用】
根据你的发现计算:
①2+4+6+…+2000;
②202+204+206+…+600.
22.某市民广场地面铺设地砖,决定采用黑白2种地砖,按如下方案铺设:首先在广场中央铺2块黑色砖(如图①),然后在黑色砖的四周铺上白色砖(如图②),再在白色砖的四周铺上黑色砖(如图③),再在黑色砖的四周铺上白色砖(如图④).这样反复更换地砖的颜色,直至铺满整个广场.观察图,解决下列问题:
(1)填表:
图形序号数 ① ② ③ ④ …
地砖总数(包括黑白地砖) 2 12 …
(2)按照这种规律第n个图形一共用去地砖多少块?(用含n的代数式表示)
参考答案
一.选择题(共10小题,满分40分)
1.解:由题知,第①行的数是以2为底数,指数从1开始连续的自然数,奇数位置为负,偶数位置为正,
∴第①行的第10个数为210,
即x=210,
第②行的数比第①行对应的数大2,
∴第②行的第10个数为210+2,
即y=210+2,
第③行的数是第①行对应数除以2所得,奇数位置为负,偶数位置为正,
∴第③行的第10个数为210÷2=29,
即z=29,
∴2x﹣y﹣2z=2×210﹣(210+2)﹣2×29=﹣2,
故选:C.
2.解:由题意可得第二行第二个的规律分别是:3×10,5×12,7×14,
∴m=9×16=144,
故选:D.
3.解:由题意可得,19右侧的数是20,
y=19×20+2=382,
故选:B.
4.解:∵a1=3,a2是a1的“友好数”,
∴a2==﹣2,
∵a3是a2的“友好数”,
∴a3==,
∵a4是a3的“友好数”,
∴a4==,
∵a5是a4的“友好数”,
∴a5==3,
……
∴每四个数是一组循环,
∵2021÷4=505…1,
∴a2021=a1=3,
故选:A.
5.解:∵每行的最后一个数是这个行的行数m的平方,
第m行的数字的个数是 2m﹣1,
∵442=1936,
所以2021在第45行,
∵452=2025,
∴45行最后一个数字是2025,
第45行有2×45﹣1=89个数字,从2025往前数4个数据得到2021,从而得出2021是第85个数据,
∴m=45,n=85,
∴m+n=45+85=130.
故选:B.
6.解:2021÷4=505…1,
∴2021应在1的位置,也就是在D处.
故选:D.
7.解:∵第①个图形需要的小木棒的根数为9,
第②个图形需要的小木棒的根数为16=9+7=9+7×1,
第③个图形需要的小木棒的根数为23=9+7+7=9+7×2,
...,
∴第n个图形需要的小木棒的根数为9+7(n﹣1)=7n+2,
∴第⑦个图形需要的小木棒的根数为7×7+2=51.
故选:A.
8.解:由图形可以得出:第①个图形 的个数为1×2﹣1,
第②个图形 的个数为2×3﹣1,
第③个图形 的个数为3×4﹣1,
第④个图形 的个数为4×5﹣1,
…,
则第n个图形 的个数为n(n+1)﹣1,
∴第⑩个图形中 的个数为10×(10+1)﹣1=109.
故选:A.
9.解:由图知,
第一个图形有3个五星,
第二个图形有3×2个五星,
第三个图形有3×3个五星,
…,
第n个图形有3n个五星,
∴第7个图形共有3×7=21个五星,
故选:C.
10.解:由图形知a1=1×2,a2=2×3,a3=3×4,
∴an=n(n+1),
∵+…+
=+++…+
=2×(1﹣+﹣+﹣+……+﹣),
=2×(1﹣)
=2×
=,
故选:A.
二.填空题(共6小题,满分30分)
11.解:(1+3+5+…+2019+2021)﹣(2+4+6+…+2018+2022)
=1+3+5+……+2017+2019+2021﹣2﹣4﹣6﹣…﹣2018﹣2022
=(1﹣2)+(3﹣4)+(5﹣6)+…+(2017﹣2018)+(2019﹣2020)+(2021﹣2022)
=
=﹣1×1011
=﹣1011.
故答案:﹣1011.
12.解:由题意得:第一行的第n个数为:(﹣2)n;
第二行的第n个数为:(﹣2)n+3;
∴第一行第9个数为:(﹣2)9=﹣512;
第二行第9个数为:﹣512+3=﹣509,
∴这两个数的和为:﹣512+(﹣509)=﹣1011.
故答案为:﹣1011.
13.解:由题知第一次输出1;
第二次输出﹣4;
第三次输出为﹣2;
第四次输出为﹣1;
第五次输出为﹣6;
第六次输出为﹣3;
第七次输出为﹣8;
第八次输出为﹣4;.....
∴从第二次开始每六次循环一次,
(2021﹣1)÷6=336......4,
∴第2021次的输出结果为﹣6,
故答案为:﹣6.
14.解:∵图①中棋子有5=1+2+1×2个,
图②中棋子有10=1+2+3+2×2个,
图③中棋子有16=1+2+3+4+3×2个,…,
∴图n中棋子有1+2+3+4+…+n+(n+1)+2n=,
∴图21中的棋子数为:=295.
故答案为:295.
15.解:由题意知,第八个图形中正方形有12+22+32+42+52+62+72+82=204(个),
故答案为:204.
16.解:∵第1个图有“六边形”的个数为:4,
第2个图有“六边形”的个数为:7=4+3=4+3×1,
第3个图有“六边形”的个数为:10=4+3+3=4+3×2,
第4个图有“六边形”的个数为:13=4+3+3+3=4+3×3,
...
∴第n个图有“六边形”的个数为:4+3(n﹣1)=3n+1,
∴第5个图有“六边形”的个数为:3×5+1=16.
故答案为:16;3n+1.
三.解答题(共6小题,满分50分)
17.解:(1)设S=1+2+22+23+…+210,
则2S=2+22+23+…+210+211,
2S﹣S=211﹣1,
S=211﹣1,
即1+2+22+23+…+210=211﹣1;
(2)设S=1+3+32+33+34+…+3n.
则3S=3+32+33+34+…+3n+3n+1,
3S﹣S=3n+1﹣1,
2S=3n+1﹣1,
S=,
即1+3+32+33+34+…+3n=.
18.解:(1)由题意知,在和式+++…中第6项为,第n项为,
故答案为:,,
(2)
=
=
=
=.
19.解:(1)第n层有(2n﹣1)个小圆圈;
故答案为:(2n﹣1);
(2)令2n﹣1=65,
解得n=33.
所以这是第33层;
故答案为:33;
(3)1+3+5+…+(2n﹣1)=n2;
故答案为:n2;
(4)(1+3+5+…+153)﹣(1+3+5+…+71)
=()2﹣()2
=772﹣362
=4633.
20.解:(1)由图1和图2得:b=m﹣18;
(2)如图3,分两种情况:
①当n>0时,e=﹣n+2,
②当n<0时,e=﹣n﹣2;
(3)由图1和图2得:a=m﹣2,b=m﹣18,c=m+2,d=m+18,
∵a+b+c+d=km,
∴m﹣2+m﹣18+m+2+m+18=km,
4m=km,
k=4,
由图3和图4得:分两种情况:
①当n>0时,e=﹣n+2,f=﹣n+18,g=﹣n﹣2,h=﹣n﹣18,
∵e+f+g+h=pn,
∴﹣n+2﹣n+18﹣n﹣2﹣n﹣18=pn,
﹣4n=pn,
p=﹣4,
∴k+3p=4+3×(﹣4)=﹣8.
②当n<0时,e=﹣n﹣2,f=﹣n﹣18,g=﹣n+2,h=﹣n+18,
∵e+f+g+h=pn,
∴﹣n﹣2﹣n﹣18﹣n+2﹣n+18=pn,
﹣4n=pn,
p=﹣4,
∴k+3p=4+3×(﹣4)=﹣8.
21.解:【规律探索】
第(1)个图形中有2=1×2张正方形纸片;
第(2)个图形中有2(1+2)=2+4=6=2×3张正方形纸片;
第(3)个图形中有2(1+2+3)=2+4+6=12=3×4张正方形纸片;
第(4)个图形中有2(1+2+3+4)=2+4+6+8=20=4×5张正方形纸片;
…
【规律归纳】
第(7)个图形中有张正方形纸片7×8=56张正方形纸片;
故答案为:56;
(2)根据上面的发现猜想:2+4+6+2n=n(n+1);
故答案为:n(n+1);
【规律应用】
①2+4+6+…+2000
=1000×1001
=1001000;
②202+204+206+…+600
=(2+4+6+…+600)﹣(2+4+6+…+200)
=300×301﹣100×101
=80200.
22.解:(1)填表:
图形序号数 ① ② ③ ④ …
地砖总数(包括黑白地砖) 2 12 30 56 …
故答案为:30,56;
(2)由图形可知:2n(2n﹣1)=4n2﹣2n,
则按照这种规律第n个图形一共用去地砖(4n2﹣2n)块.
一.选择题(共10小题,满分40分)
1.观察下面三行数:
﹣2、4、﹣8、16、﹣32、64、……①
0、6、﹣6、18、﹣30、66、……②
﹣1、2、﹣4、8、﹣16、32、……③
设x、y、z分别为第①②③行的第10个数,则2x﹣y﹣2z的值为( )
A.22001 B.0 C.﹣2 D.2
2.如图各正方形中的四个数字之间都有相同的规律,根据这种规律,m的值是( )
A.74 B.104 C.126 D.144
3.如图所示:下列各三角形中的三个数均有相同的规律,由此规律最后一个三角形中,y的值是( )
A.380 B.382 C.384 D.386
4.若a≠2,则我们把称为a的“友好数”,如3的“友好数”是,﹣2的“友好数”是,已知a1=3,a2是a1的“友好数”,a3是a2的“友好数”,a4是a3的“友好数”,……,依此类推,则a2021=( )
A.3 B.﹣2 C. D.
5.右边是一个按某种规律排列的数阵:根据规律,自然数2021应该排在从上向下数的第m行,是该行中的从左向右数的第n个数,那么m+n的值是( )
A.131 B.130 C.129 D.128
6.将正整数按如图所示的位置顺序排列:
根据排列规律,则2021应在( )
A.A处 B.B处 C.C处 D.D处
7.用一样长的小木棒按图中的方式搭图形.图①中小木棒的根数为9,图②中小木棒的根数为16,图③中小木棒的根数为23,按照这种规律搭下去,搭第7个图形需要小木棒的根数是( )
A.51 B.63 C.49 D.72
8.下列图形都是由同样大小的 按一定的规律组成,其中第①个图形共有1个 ,第②个图形共有5个 ,第③个图形共有11个 ,第④个图形共有19个 ,…,依此规律,则第⑩个图形中 的个数为( )
A.109 B.99 C.89 D.71
9.观察下列图形:它们是按一定规律排列的,依照此规律,第7个图形共有( )个五星.
A.14 B.18 C.21 D.28
10.如图所示,将形状大小完全相同的“ ”按照一定规律摆成下列图形,第1幅图中“ ”的个数为a1,第2幅图中“ ”的个数为a2,第3幅图中“ ”的个数为a3,…,以此类推,的值为( )
A. B. C. D.
二.填空题(共6小题,满分30分)
11.(1+3+5+…+2017+2019+2021)﹣(2+4+6+…+2018+2022)= .
12.观察下面两行数:
﹣2,4,﹣8,16,﹣32,64,…
1,7,﹣5,19,﹣29,67,…
根据你发现的规律,取每行数的第9个数,它们的和等于 .
13.如图所示,在这个数据运算程序中,若开始输入的x值为2,结果输出的是1,返回进行第二次运算则输出的是﹣4,…,则第2021次输出的结果是 .
14.如图图形是由同样大小的棋子按照一定规律排列而成的,其中图①中有5个棋子,图②中有10个棋子,图③中有16个棋子,…,则图中有 个棋子.
15.如图,第一个图形中有1个正方形;第二个图形中有5个正方形;第三个图形中有14个正方形;则按此规律第八个图形有 个正方形.
16.观察下列的“蜂窝图”,则第5个图案中的“六边形”的个数是 ,第n个图案中的“六边形”的个数是 .(用含有n的代数式表示)
三.解答题(共6小题,满分50分)
17.阅读材料,回答问题:求值1+2+22+23+…+22020.
解:设S=1+2+22+23+…+22020.①
将等式两边同时乘2得,2S=2+22+23+…+22020+22021.②
②﹣①得,2S﹣S=22021﹣1,即S=1+2+22+23+…+22020=22021﹣1.
请你仿照此法计算:
(1)1+2+22+23+…+210;
(2)1+3+32+33+…+3n(其中n为正整数).
18.阅读下列材料:
∵=(1﹣),
=(﹣),
=(﹣),
……
=(﹣),
∴+++…+
=(1﹣)+(﹣)+(﹣)+……+(﹣)
=(1﹣+﹣+﹣+……+﹣)
=(1﹣)
=.
解答下列问题:
(1)在+++...中,第6项为 ,第n项是 .
(2)求的值.
19.观察图,解答下列问题.
(1)图中的小圆圈被折线隔开分成六层,第一层有1个小圆圈,第二层有3个圆圈,第三层有5个圆圈,…,第六层有11个圆圈.如果要你继续画下去,第n层有 个小圆圈.
(2)某一层上有65个圆圈,这是第 层.
(3)数图中的圆圈个数可以有多种不同的方法.
比如:前两层的圆圈个数和为(1+3)或22,
由此得,1+3=22.
同样:
由前三层的圆圈个数和得:1+3+5=32.
由前四层的圆圈个数和得:1+3+5+7=42.
…
根据上述规律,从1开始的n个连续奇数之和是多少?用n的代数式把它表示出来 .
(4)运用(3)中的规律计算:73+75+77+…+153.
20.图1为奇数排成的数表,用十字框任意框出5个数,记框内中间这个数为m,其它四个数分别记为a,b,c,d(如图2);图3为按某一规律排成的另一个数表,用十字框任意框出5个数,记框内中间这个数为n,其它四个数记为e,f,g,h(如图4).
(1)请用含m的代数式表示b.
(2)请用含n的代数式表示e.
(3)若a+b+c+d=km,e+f+g+h=pn,求k+3p的值.
21.我国著名数学家华罗庚先生说过:“数形结合百股好,隔裂分家万事休”,数形结合的思想方法在数学中应用极为广泛.
【规律探索】用同样大小的两种不同颜色的正方形纸片,按如图方式拼成长方形:
第(1)个图形中有2张正方形纸片;
第(2)个图形中有2(1+2)=2+4=6张正方形纸片;
第(3)个图形中有2(1+2+3)=2+4+6=12张正方形纸片;
第(4)个图形中有2(1+2+3+4)=2+4+6+8=20张正方形纸片;
…
请你观察上述图形与算式,完成下列问题:
【规律归纳】
(1)第(7)个图形中有 张正方形纸片(直接写出结果);
(2)根据上面的发现我们可以猜想:2+4+6+2n= (用含n的代数式表示);
【规律应用】
根据你的发现计算:
①2+4+6+…+2000;
②202+204+206+…+600.
22.某市民广场地面铺设地砖,决定采用黑白2种地砖,按如下方案铺设:首先在广场中央铺2块黑色砖(如图①),然后在黑色砖的四周铺上白色砖(如图②),再在白色砖的四周铺上黑色砖(如图③),再在黑色砖的四周铺上白色砖(如图④).这样反复更换地砖的颜色,直至铺满整个广场.观察图,解决下列问题:
(1)填表:
图形序号数 ① ② ③ ④ …
地砖总数(包括黑白地砖) 2 12 …
(2)按照这种规律第n个图形一共用去地砖多少块?(用含n的代数式表示)
参考答案
一.选择题(共10小题,满分40分)
1.解:由题知,第①行的数是以2为底数,指数从1开始连续的自然数,奇数位置为负,偶数位置为正,
∴第①行的第10个数为210,
即x=210,
第②行的数比第①行对应的数大2,
∴第②行的第10个数为210+2,
即y=210+2,
第③行的数是第①行对应数除以2所得,奇数位置为负,偶数位置为正,
∴第③行的第10个数为210÷2=29,
即z=29,
∴2x﹣y﹣2z=2×210﹣(210+2)﹣2×29=﹣2,
故选:C.
2.解:由题意可得第二行第二个的规律分别是:3×10,5×12,7×14,
∴m=9×16=144,
故选:D.
3.解:由题意可得,19右侧的数是20,
y=19×20+2=382,
故选:B.
4.解:∵a1=3,a2是a1的“友好数”,
∴a2==﹣2,
∵a3是a2的“友好数”,
∴a3==,
∵a4是a3的“友好数”,
∴a4==,
∵a5是a4的“友好数”,
∴a5==3,
……
∴每四个数是一组循环,
∵2021÷4=505…1,
∴a2021=a1=3,
故选:A.
5.解:∵每行的最后一个数是这个行的行数m的平方,
第m行的数字的个数是 2m﹣1,
∵442=1936,
所以2021在第45行,
∵452=2025,
∴45行最后一个数字是2025,
第45行有2×45﹣1=89个数字,从2025往前数4个数据得到2021,从而得出2021是第85个数据,
∴m=45,n=85,
∴m+n=45+85=130.
故选:B.
6.解:2021÷4=505…1,
∴2021应在1的位置,也就是在D处.
故选:D.
7.解:∵第①个图形需要的小木棒的根数为9,
第②个图形需要的小木棒的根数为16=9+7=9+7×1,
第③个图形需要的小木棒的根数为23=9+7+7=9+7×2,
...,
∴第n个图形需要的小木棒的根数为9+7(n﹣1)=7n+2,
∴第⑦个图形需要的小木棒的根数为7×7+2=51.
故选:A.
8.解:由图形可以得出:第①个图形 的个数为1×2﹣1,
第②个图形 的个数为2×3﹣1,
第③个图形 的个数为3×4﹣1,
第④个图形 的个数为4×5﹣1,
…,
则第n个图形 的个数为n(n+1)﹣1,
∴第⑩个图形中 的个数为10×(10+1)﹣1=109.
故选:A.
9.解:由图知,
第一个图形有3个五星,
第二个图形有3×2个五星,
第三个图形有3×3个五星,
…,
第n个图形有3n个五星,
∴第7个图形共有3×7=21个五星,
故选:C.
10.解:由图形知a1=1×2,a2=2×3,a3=3×4,
∴an=n(n+1),
∵+…+
=+++…+
=2×(1﹣+﹣+﹣+……+﹣),
=2×(1﹣)
=2×
=,
故选:A.
二.填空题(共6小题,满分30分)
11.解:(1+3+5+…+2019+2021)﹣(2+4+6+…+2018+2022)
=1+3+5+……+2017+2019+2021﹣2﹣4﹣6﹣…﹣2018﹣2022
=(1﹣2)+(3﹣4)+(5﹣6)+…+(2017﹣2018)+(2019﹣2020)+(2021﹣2022)
=
=﹣1×1011
=﹣1011.
故答案:﹣1011.
12.解:由题意得:第一行的第n个数为:(﹣2)n;
第二行的第n个数为:(﹣2)n+3;
∴第一行第9个数为:(﹣2)9=﹣512;
第二行第9个数为:﹣512+3=﹣509,
∴这两个数的和为:﹣512+(﹣509)=﹣1011.
故答案为:﹣1011.
13.解:由题知第一次输出1;
第二次输出﹣4;
第三次输出为﹣2;
第四次输出为﹣1;
第五次输出为﹣6;
第六次输出为﹣3;
第七次输出为﹣8;
第八次输出为﹣4;.....
∴从第二次开始每六次循环一次,
(2021﹣1)÷6=336......4,
∴第2021次的输出结果为﹣6,
故答案为:﹣6.
14.解:∵图①中棋子有5=1+2+1×2个,
图②中棋子有10=1+2+3+2×2个,
图③中棋子有16=1+2+3+4+3×2个,…,
∴图n中棋子有1+2+3+4+…+n+(n+1)+2n=,
∴图21中的棋子数为:=295.
故答案为:295.
15.解:由题意知,第八个图形中正方形有12+22+32+42+52+62+72+82=204(个),
故答案为:204.
16.解:∵第1个图有“六边形”的个数为:4,
第2个图有“六边形”的个数为:7=4+3=4+3×1,
第3个图有“六边形”的个数为:10=4+3+3=4+3×2,
第4个图有“六边形”的个数为:13=4+3+3+3=4+3×3,
...
∴第n个图有“六边形”的个数为:4+3(n﹣1)=3n+1,
∴第5个图有“六边形”的个数为:3×5+1=16.
故答案为:16;3n+1.
三.解答题(共6小题,满分50分)
17.解:(1)设S=1+2+22+23+…+210,
则2S=2+22+23+…+210+211,
2S﹣S=211﹣1,
S=211﹣1,
即1+2+22+23+…+210=211﹣1;
(2)设S=1+3+32+33+34+…+3n.
则3S=3+32+33+34+…+3n+3n+1,
3S﹣S=3n+1﹣1,
2S=3n+1﹣1,
S=,
即1+3+32+33+34+…+3n=.
18.解:(1)由题意知,在和式+++…中第6项为,第n项为,
故答案为:,,
(2)
=
=
=
=.
19.解:(1)第n层有(2n﹣1)个小圆圈;
故答案为:(2n﹣1);
(2)令2n﹣1=65,
解得n=33.
所以这是第33层;
故答案为:33;
(3)1+3+5+…+(2n﹣1)=n2;
故答案为:n2;
(4)(1+3+5+…+153)﹣(1+3+5+…+71)
=()2﹣()2
=772﹣362
=4633.
20.解:(1)由图1和图2得:b=m﹣18;
(2)如图3,分两种情况:
①当n>0时,e=﹣n+2,
②当n<0时,e=﹣n﹣2;
(3)由图1和图2得:a=m﹣2,b=m﹣18,c=m+2,d=m+18,
∵a+b+c+d=km,
∴m﹣2+m﹣18+m+2+m+18=km,
4m=km,
k=4,
由图3和图4得:分两种情况:
①当n>0时,e=﹣n+2,f=﹣n+18,g=﹣n﹣2,h=﹣n﹣18,
∵e+f+g+h=pn,
∴﹣n+2﹣n+18﹣n﹣2﹣n﹣18=pn,
﹣4n=pn,
p=﹣4,
∴k+3p=4+3×(﹣4)=﹣8.
②当n<0时,e=﹣n﹣2,f=﹣n﹣18,g=﹣n+2,h=﹣n+18,
∵e+f+g+h=pn,
∴﹣n﹣2﹣n﹣18﹣n+2﹣n+18=pn,
﹣4n=pn,
p=﹣4,
∴k+3p=4+3×(﹣4)=﹣8.
21.解:【规律探索】
第(1)个图形中有2=1×2张正方形纸片;
第(2)个图形中有2(1+2)=2+4=6=2×3张正方形纸片;
第(3)个图形中有2(1+2+3)=2+4+6=12=3×4张正方形纸片;
第(4)个图形中有2(1+2+3+4)=2+4+6+8=20=4×5张正方形纸片;
…
【规律归纳】
第(7)个图形中有张正方形纸片7×8=56张正方形纸片;
故答案为:56;
(2)根据上面的发现猜想:2+4+6+2n=n(n+1);
故答案为:n(n+1);
【规律应用】
①2+4+6+…+2000
=1000×1001
=1001000;
②202+204+206+…+600
=(2+4+6+…+600)﹣(2+4+6+…+200)
=300×301﹣100×101
=80200.
22.解:(1)填表:
图形序号数 ① ② ③ ④ …
地砖总数(包括黑白地砖) 2 12 30 56 …
故答案为:30,56;
(2)由图形可知:2n(2n﹣1)=4n2﹣2n,
则按照这种规律第n个图形一共用去地砖(4n2﹣2n)块.
