2021-2022学年鲁教版(五四制)六年级数学上册3.7探索与表达规律 同步达标训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)六年级数学上册3.7探索与表达规律 同步达标训练(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 255.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 13:40:38 | ||
图片预览




文档简介
2021-2022学年鲁教版六年级数学上册《3.7探索与表达规律》同步达标训练(附答案)
1.如图所示,第一个图形共6个小圆圈,第二个图形共12个小圆圈,第三个图形共20个小圆圈,则按此规律,第8个图形共( )个小圆圈.
A.56 B.72 C.64 D.90
2.观察图中正方形四个顶点所标的数字规律,可知数2025应标在( )
A.第507个正方形的左上角
B.第507个正方形的右下角
C.第506个正方形的左上角
D.第506个正方形的右下角
3.通过对现象的观察、分析,从特殊到一般地探索这类现象的规律、提出猜想的思想方法称为归纳.请用归纳思想解决下列问题:三角形有3个顶点,如果在它的内部再画n个点,并以(n+3)个点为顶点画三角形,那么最多可以剪得的三角形个数为( )
三角形内点的个数 图形 最多剪出的小三角形个数
1 3
2 5
3 7
… … …
A.2n﹣3 B.2n﹣1 C.2n+1 D.2n+3
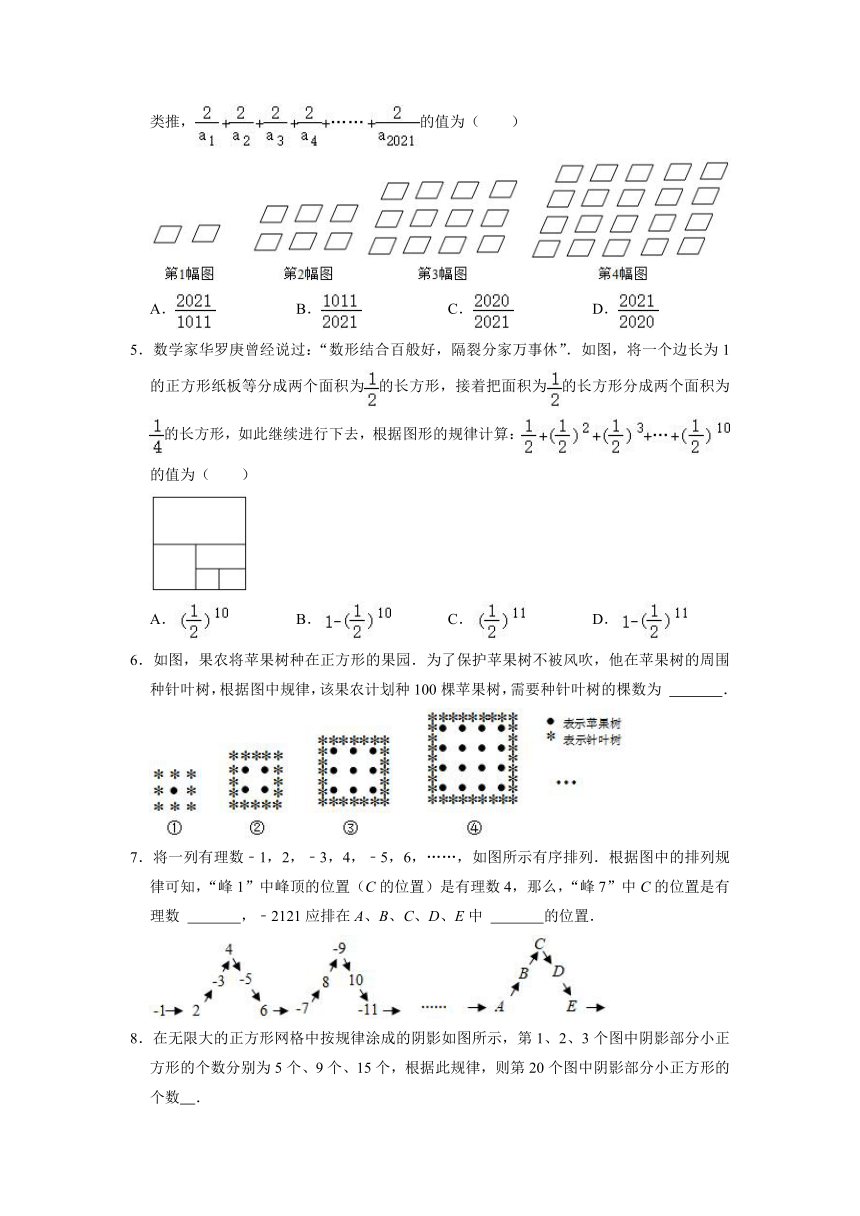
4.如图所示,将形状大小完全相同的“ ”按照一定规律摆成下列图形,第1幅图中“ ”的个数为a1,第2幅图中“ ”的个数为a2,第3幅图中“ ”的个数为a3,…,以此类推,的值为( )
A. B. C. D.
5.数学家华罗庚曾经说过:“数形结合百般好,隔裂分家万事休”.如图,将一个边长为1的正方形纸板等分成两个面积为的长方形,接着把面积为的长方形分成两个面积为的长方形,如此继续进行下去,根据图形的规律计算:的值为( )
A. B. C. D.
6.如图,果农将苹果树种在正方形的果园.为了保护苹果树不被风吹,他在苹果树的周围种针叶树,根据图中规律,该果农计划种100棵苹果树,需要种针叶树的棵数为 .
7.将一列有理数﹣1,2,﹣3,4,﹣5,6,……,如图所示有序排列.根据图中的排列规律可知,“峰1”中峰顶的位置(C的位置)是有理数4,那么,“峰7”中C的位置是有理数 ,﹣2121应排在A、B、C、D、E中 的位置.
在无限大的正方形网格中按规律涂成的阴影如图所示,第1、2、3个图中阴影部分小正方形的个数分别为5个、9个、15个,根据此规律,则第20个图中阴影部分小正方形的个数 .
9.如图,在正方形ABC B1中,AB=1,AB与直线l的夹角为30°,延长C B1交直线l于点 A1,做正方形 A1B1C1B2,延长 C1B2交直线l于点 A2,做正方形 A2B2C2B3;延长 C2B3交直线l于点 A3,…,依次规律,则 A2021B2021= .
10.探索规律,观察图中由※组成的图案和算式,解答问题:(1)请猜想1+3+5+7+9+…+19= ;
(2)请猜想1+3+5+7+9+…+(2n﹣1)= .
11.观察图1至图5中小黑点的摆放规律,并按照这样的规律继续摆放.
解答下列问题:
(1)填表:(n代表第n个图形)
n 1 2 3 4 5 … n
黑点个数 1 3 7 13 …
(2)当n=100时,黑点个数为 ;
(3)当n= 时,黑点个数为381.
12.某市民广场地面铺设地砖,决定采用黑白2种地砖,按如下方案铺设:首先在广场中央铺2块黑色砖(如图①),然后在黑色砖的四周铺上白色砖(如图②),再在白色砖的四周铺上黑色砖(如图③),再在黑色砖的四周铺上白色砖(如图④).这样反复更换地砖的颜色,直至铺满整个广场.观察图,解决下列问题:
(1)填表:
图形序号数 ① ② ③ ④ …
地砖总数(包括黑白地砖) 2 12 …
(2)按照这种规律第n个图形一共用去地砖多少块?(用含n的代数式表示)
13.(1)仔细观察下列式子:(a×b)2=a2×b2,(a×b)3=a3×b3,(a×b)4=a4×b4.
猜一猜:(a×b)100= .归纳得出:(a×b)n= .
请应用上述性质计算:(﹣)2021×42022= .
(2)如图是由从1开始的连续自然数组成的数表,观察规律并完成各题的解答.
①表中第8行的最后一个数是 ,它是自然数 的平方,第8行共有 个数;
②用含n的代数式表示:第n行的第一个数是 ,最后一个数是 ,第n行共有 个数.
14.观察下列由棱长为1的小正方体摆成的图形,寻找规律,如图①共有1个小立方体,其中1个看得见,0个看不见;如图②:共有8个小立方体,其中7个看得见,1个看不见;如图③:共有27个小立方体,其中19个看得见,8个看不见…
(1)写出第⑥个图中看不见的小立方体有 个;
(2)猜想并写出与第n个图形中看不见的小立方体的个数.
15.将正整数1至2024按一定规律排列成如图所示的8列,规定从上到下依次为第1行,第2行,第3行,…从左往右依次为第1列至第8列.
(1)数56在第 行 列;
(2)平移图中带阴影的方框,使方框框住相邻的三个数,若被框住的三个数中最大的一个数为x,则被框的三个数的和能否等于2019?若能,请求出x;若不能,请说明理由.
16.我国著名数学家华罗庚先生说过:“数形结合百股好,隔裂分家万事休”,数形结合的思想方法在数学中应用极为广泛.
【规律探索】用同样大小的两种不同颜色的正方形纸片,按如图方式拼成长方形:
第(1)个图形中有2张正方形纸片;
第(2)个图形中有2(1+2)=2+4=6张正方形纸片;
第(3)个图形中有2(1+2+3)=2+4+6=12张正方形纸片;
第(4)个图形中有2(1+2+3+4)=2+4+6+8=20张正方形纸片;
…
请你观察上述图形与算式,完成下列问题:
【规律归纳】
(1)第(7)个图形中有 张正方形纸片(直接写出结果);
(2)根据上面的发现我们可以猜想:2+4+6+2n= (用含n的代数式表示);
【规律应用】
根据你的发现计算:
①2+4+6+…+2000;
②202+204+206+…+600.
17.观察图,解答下列问题.
(1)图中的小圆圈被折线隔开分成六层,第一层有1个小圆圈,第二层有3个圆圈,第三层有5个圆圈,…,第六层有11个圆圈.如果要你继续画下去,第n层有 个小圆圈.
(2)某一层上有65个圆圈,这是第 层.
(3)数图中的圆圈个数可以有多种不同的方法.
比如:前两层的圆圈个数和为(1+3)或22,
由此得,1+3=22.
同样:
由前三层的圆圈个数和得:1+3+5=32.
由前四层的圆圈个数和得:1+3+5+7=42.
…
根据上述规律,从1开始的n个连续奇数之和是多少?用n的代数式把它表示出来 .
(4)运用(3)中的规律计算:73+75+77+…+153.
18.图1为奇数排成的数表,用十字框任意框出5个数,记框内中间这个数为m,其它四个数分别记为a,b,c,d(如图2);图3为按某一规律排成的另一个数表,用十字框任意框出5个数,记框内中间这个数为n,其它四个数记为e,f,g,h(如图4).
(1)请用含m的代数式表示b.
(2)请用含n的代数式表示e.
(3)若a+b+c+d=km,e+f+g+h=pn,求k+3p的值.
19.观察图形,解答问题:
(1)按下表已填写的形式填写表中的空格:
图① 图② 图③
三个角上三个数的积 1×(﹣1)×2=﹣2 (﹣3)×(﹣4)×(﹣5)=﹣60
三个角上三个数的和 1+(﹣1)+2=2 (﹣3)+(﹣4)+(﹣5)=﹣12
积与和的商 (﹣2)÷2=﹣1
(2)请用你发现的规律求出图④中的数x和图⑤中的数y.
参考答案
1.解:由图知,
第1个图形共有小圆圈的个数为:6=2×3,
第2个图形共有小圆圈的个数为:12=3×4,
第3个图形共有小圆圈的个数为:20=4×5,
第4个图形共有小圆圈的个数为:30=5×6,
...,
第n个图形共有小圆圈的个数为:(n+1)(n+2),
∴第8个图形共有小圆圈的个数为:9×10=90,
故选:D.
2.解:根据图形的变化可知,每四个数一个正方形,且四个数在正方形上的相对位置是相同的,
∵2025÷4=506......1,
∴2025在第507个正方形右下角位置上,
故选:B.
3.解:∵当三角形内点的个数为1时,最多可以剪得3个三角形;
当三角形内点的个数为2时,最多可以剪得5个三角形;
当三角形内点的个数为3时,最多可以剪得7个三角形;
当三角形内点的个数为4时,最多可以剪得9个三角形;
∴变化规律是:三角形内的点每增加1个,最多剪得的三角形增加2个;
∴当三角形内点的个数为n时,最多可以剪得(2n+1)个三角形;
故选:C.
4.解:由图形知a1=1×2,a2=2×3,a3=3×4,
∴an=n(n+1),
∵+…+
=+++…+
=2×(1﹣+﹣+﹣+……+﹣),
=2×(1﹣)
=2×
=,
故选:A.
5.解:=,
故选:B.
6.解:∵第1个图形中苹果树的棵数是1,针叶树的棵数是8,
第2个图形中苹果树的棵数是4=22,针叶树的棵数是16=8×2,
第3个图形中苹果树的棵数是9=32,针叶树的棵数为是24=8×3,
第4个图形中苹果树的棵数为是16=42,针叶树的棵数是32=8×4,
…,
∴第n个图形中苹果树的棵数是n2,针叶树的棵数是8n,
∴当有100棵苹果树时,即n2=100,解得:n=10,
∴需要种针叶树的数量为:8×10=80(棵).
故答案为:80.
7.解:由图知,每五个数一个峰,且第奇数个峰值是正偶数,第偶数个峰值是负奇数,
故“峰7”中C的位置是7×5﹣1=34,
∵(2121﹣1)÷5=424,
∴﹣2121在E位置,
故答案为:34,E.
8.解:根据所给的图形可得:
第一个图有:5=1+1+3(个),
第二个图有:9=4+2+3(个),
第三个图有:15=9+3+3(个),
…,
则第n个为n2+n+3,
第20个图有:400+20+3=423(个),
故答案为:423.
9.解:∵四边形ABCB1为正方形,
∴AB1=AB=1,
∵A1C∥AB,
∴∠B1A1A=30°,
∴A1B1=AB1=,AA1=2AB1=2,
∵四边形A1B1C1B2为正方形,
∴A1B2=A1B1=,
∵A2C1∥A1B1,
∴∠B2A2A1=30°,
∴A2B2=A1B2=×=()2,
……
∴A2021B2021=()2021,
故答案为:()2021.
10.解:(1)由1+3=4=22,
1+3+5=9=32,
1+3+5+7=16=42,
1+3+5+7+9=25=52,
…,
∵1+3+5+7+9+…+19共有10个数,
∴1+3+5+7+9+…+19=102=100.
故答案为:100;
(2)由(1)得,1+3+5+7+9+…+(2n﹣1)=n2.
故答案为:n2.
11.解:(1)图1黑点的个数是:1;
图2黑点的个数是:3=1+(2﹣1)×2;
图3黑点的个数是:7=1+(3﹣1)×3;
…
图n黑点的个数为:1+(n﹣1) n=n2﹣n+1;
故图5中黑点的个数为:52﹣5+1=21,
故答案为:21;n2﹣n+1;
(2)当n=100时,1002﹣100+1=9901;
故答案为:9901;
(3)由题意得:n2﹣n+1=381,
解得:n=20,n=﹣19(舍去),
故答案为:20.
12.解:(1)填表:
图形序号数 ① ② ③ ④ …
地砖总数(包括黑白地砖) 2 12 30 56 …
故答案为:30,56;
(2)由图形可知:2n(2n﹣1)=4n2﹣2n,
则按照这种规律第n个图形一共用去地砖(4n2﹣2n)块.
13.解:(1)(a×b)100=a100×b100.
归纳得出:(a×b)n=an×bn.
(﹣)2021×42022=﹣()2021×42022=﹣(×4)2021×4=﹣12021×4=﹣4;
故答案为:a100×b100,an×bn,﹣4.
(2)①表中第8行的最后一个数是64,它是自然数8的平方,第8行共有15个数;
②用含n的代数式表示:第n行的第一个数是(n﹣1)2+1,最后一个数是n2,第n行共有(2n﹣1)个数.
故答案为:64,8,15;(n﹣1)2+1,n2,(2n﹣1).
14.解:(1)当高有1个立方体时,1=1,0=(1﹣1)3=03;
当高有2个立方体时,8=23,1=13=(2﹣1)3;
当高有3个立方体时,27=33,8=(3﹣1)3=23;
当高有4个立方体时,64=43,27=(4﹣1)3=33;
当高有5个立方体时,125=53,64=(5﹣1)3=43;
当高有6个立方体时,216=63,125=(6﹣1)3=53;
故答案为:125.
(2)由(1)可知,当高有n个立方体时,看不见的小立方体的个数为(n﹣1)3个.
15.解:(1)∵56=7×8,
∴数56在第7行8列;
故答案为:7;8;
(2)∵设被框住的三个数中,最大的一个数为x,则另外两个数为x﹣2,x﹣1,
∴三个数之和为x﹣2+x﹣1+x=3x﹣3.
根据题意得:3x﹣3=2019,
解得:x=674,
∵674=84×8+2,
∴数674在第85行2列,不符合题意,
∴三个数的和不可以等于2019,此时x的值为672;
3x﹣3=2019,
解得:x=674,
∵674=84×8+2,
∴数674在第85行2列,
∵方框框住相邻的三个数中最大的数x,至少位于第3列,
∴三个数的和不可以等于2019.
16.解:【规律探索】
第(1)个图形中有2=1×2张正方形纸片;
第(2)个图形中有2(1+2)=2+4=6=2×3张正方形纸片;
第(3)个图形中有2(1+2+3)=2+4+6=12=3×4张正方形纸片;
第(4)个图形中有2(1+2+3+4)=2+4+6+8=20=4×5张正方形纸片;
…
【规律归纳】
第(7)个图形中有张正方形纸片7×8=56张正方形纸片;
故答案为:56;
(2)根据上面的发现猜想:2+4+6+2n=n(n+1);
故答案为:n(n+1);
【规律应用】
①2+4+6+…+2000
=1000×1001
=1001000;
②202+204+206+…+600
=(2+4+6+…+600)﹣(2+4+6+…+200)
=300×301﹣100×101
=80200.
17.解:(1)第n层有(2n﹣1)个小圆圈;
故答案为:(2n﹣1);
(2)令2n﹣1=65,
解得n=33.
所以这是第33层;
故答案为:33;
(3)1+3+5+…+(2n﹣1)=n2;
故答案为:n2;
(4)(1+3+5+…+153)﹣(1+3+5+…+71)
=()2﹣()2
=772﹣362
=4633.
18.解:(1)由图1和图2得:b=m﹣18;
(2)如图3,分两种情况:
①当n>0时,e=﹣n+2,
②当n<0时,e=﹣n﹣2;
(3)由图1和图2得:a=m﹣2,b=m﹣18,c=m+2,d=m+18,
∵a+b+c+d=km,
∴m﹣2+m﹣18+m+2+m+18=km,
4m=km,
k=4,
由图3和图4得:分两种情况:
①当n>0时,e=﹣n+2,f=﹣n+18,g=﹣n﹣2,h=﹣n﹣18,
∵e+f+g+h=pn,
∴﹣n+2﹣n+18﹣n﹣2﹣n﹣18=pn,
﹣4n=pn,
p=﹣4,
∴k+3p=4+3×(﹣4)=﹣8.
②当n<0时,e=﹣n﹣2,f=﹣n﹣18,g=﹣n+2,h=﹣n+18,
∵e+f+g+h=pn,
∴﹣n﹣2﹣n﹣18﹣n+2﹣n+18=pn,
﹣4n=pn,
p=﹣4,
∴k+3p=4+3×(﹣4)=﹣8.
19.解:(1)图②:(﹣60)÷(﹣12)=5,
图③:(﹣2)×(﹣5)×17=170,
(﹣2)+(﹣5)+17=10,
170÷10=17.
图① 图② 图③
三个角上三个数的积 1×(﹣1)×2=﹣2 (﹣3)×(﹣4)×(﹣5)=﹣60 (﹣2)×(﹣5)×17=170
三个角上三个数的和 1+(﹣1)+2=2 (﹣3)+(﹣4)+(﹣5)=﹣12 (﹣2)+(﹣5)+17=10
积与和的商 ﹣2÷2=﹣1, (﹣60)÷(﹣12)=5, 170÷10=17
(2)图④:5×(﹣8)×(﹣9)=360,
5+(﹣8)+(﹣9)=﹣12,
x=360÷(﹣12)×2=﹣60,
图⑤:1×3×(﹣6)=﹣18,
1+3+(﹣6)=﹣2,
y=﹣18÷(﹣2)×2=18.
1.如图所示,第一个图形共6个小圆圈,第二个图形共12个小圆圈,第三个图形共20个小圆圈,则按此规律,第8个图形共( )个小圆圈.
A.56 B.72 C.64 D.90
2.观察图中正方形四个顶点所标的数字规律,可知数2025应标在( )
A.第507个正方形的左上角
B.第507个正方形的右下角
C.第506个正方形的左上角
D.第506个正方形的右下角
3.通过对现象的观察、分析,从特殊到一般地探索这类现象的规律、提出猜想的思想方法称为归纳.请用归纳思想解决下列问题:三角形有3个顶点,如果在它的内部再画n个点,并以(n+3)个点为顶点画三角形,那么最多可以剪得的三角形个数为( )
三角形内点的个数 图形 最多剪出的小三角形个数
1 3
2 5
3 7
… … …
A.2n﹣3 B.2n﹣1 C.2n+1 D.2n+3
4.如图所示,将形状大小完全相同的“ ”按照一定规律摆成下列图形,第1幅图中“ ”的个数为a1,第2幅图中“ ”的个数为a2,第3幅图中“ ”的个数为a3,…,以此类推,的值为( )
A. B. C. D.
5.数学家华罗庚曾经说过:“数形结合百般好,隔裂分家万事休”.如图,将一个边长为1的正方形纸板等分成两个面积为的长方形,接着把面积为的长方形分成两个面积为的长方形,如此继续进行下去,根据图形的规律计算:的值为( )
A. B. C. D.
6.如图,果农将苹果树种在正方形的果园.为了保护苹果树不被风吹,他在苹果树的周围种针叶树,根据图中规律,该果农计划种100棵苹果树,需要种针叶树的棵数为 .
7.将一列有理数﹣1,2,﹣3,4,﹣5,6,……,如图所示有序排列.根据图中的排列规律可知,“峰1”中峰顶的位置(C的位置)是有理数4,那么,“峰7”中C的位置是有理数 ,﹣2121应排在A、B、C、D、E中 的位置.
在无限大的正方形网格中按规律涂成的阴影如图所示,第1、2、3个图中阴影部分小正方形的个数分别为5个、9个、15个,根据此规律,则第20个图中阴影部分小正方形的个数 .
9.如图,在正方形ABC B1中,AB=1,AB与直线l的夹角为30°,延长C B1交直线l于点 A1,做正方形 A1B1C1B2,延长 C1B2交直线l于点 A2,做正方形 A2B2C2B3;延长 C2B3交直线l于点 A3,…,依次规律,则 A2021B2021= .
10.探索规律,观察图中由※组成的图案和算式,解答问题:(1)请猜想1+3+5+7+9+…+19= ;
(2)请猜想1+3+5+7+9+…+(2n﹣1)= .
11.观察图1至图5中小黑点的摆放规律,并按照这样的规律继续摆放.
解答下列问题:
(1)填表:(n代表第n个图形)
n 1 2 3 4 5 … n
黑点个数 1 3 7 13 …
(2)当n=100时,黑点个数为 ;
(3)当n= 时,黑点个数为381.
12.某市民广场地面铺设地砖,决定采用黑白2种地砖,按如下方案铺设:首先在广场中央铺2块黑色砖(如图①),然后在黑色砖的四周铺上白色砖(如图②),再在白色砖的四周铺上黑色砖(如图③),再在黑色砖的四周铺上白色砖(如图④).这样反复更换地砖的颜色,直至铺满整个广场.观察图,解决下列问题:
(1)填表:
图形序号数 ① ② ③ ④ …
地砖总数(包括黑白地砖) 2 12 …
(2)按照这种规律第n个图形一共用去地砖多少块?(用含n的代数式表示)
13.(1)仔细观察下列式子:(a×b)2=a2×b2,(a×b)3=a3×b3,(a×b)4=a4×b4.
猜一猜:(a×b)100= .归纳得出:(a×b)n= .
请应用上述性质计算:(﹣)2021×42022= .
(2)如图是由从1开始的连续自然数组成的数表,观察规律并完成各题的解答.
①表中第8行的最后一个数是 ,它是自然数 的平方,第8行共有 个数;
②用含n的代数式表示:第n行的第一个数是 ,最后一个数是 ,第n行共有 个数.
14.观察下列由棱长为1的小正方体摆成的图形,寻找规律,如图①共有1个小立方体,其中1个看得见,0个看不见;如图②:共有8个小立方体,其中7个看得见,1个看不见;如图③:共有27个小立方体,其中19个看得见,8个看不见…
(1)写出第⑥个图中看不见的小立方体有 个;
(2)猜想并写出与第n个图形中看不见的小立方体的个数.
15.将正整数1至2024按一定规律排列成如图所示的8列,规定从上到下依次为第1行,第2行,第3行,…从左往右依次为第1列至第8列.
(1)数56在第 行 列;
(2)平移图中带阴影的方框,使方框框住相邻的三个数,若被框住的三个数中最大的一个数为x,则被框的三个数的和能否等于2019?若能,请求出x;若不能,请说明理由.
16.我国著名数学家华罗庚先生说过:“数形结合百股好,隔裂分家万事休”,数形结合的思想方法在数学中应用极为广泛.
【规律探索】用同样大小的两种不同颜色的正方形纸片,按如图方式拼成长方形:
第(1)个图形中有2张正方形纸片;
第(2)个图形中有2(1+2)=2+4=6张正方形纸片;
第(3)个图形中有2(1+2+3)=2+4+6=12张正方形纸片;
第(4)个图形中有2(1+2+3+4)=2+4+6+8=20张正方形纸片;
…
请你观察上述图形与算式,完成下列问题:
【规律归纳】
(1)第(7)个图形中有 张正方形纸片(直接写出结果);
(2)根据上面的发现我们可以猜想:2+4+6+2n= (用含n的代数式表示);
【规律应用】
根据你的发现计算:
①2+4+6+…+2000;
②202+204+206+…+600.
17.观察图,解答下列问题.
(1)图中的小圆圈被折线隔开分成六层,第一层有1个小圆圈,第二层有3个圆圈,第三层有5个圆圈,…,第六层有11个圆圈.如果要你继续画下去,第n层有 个小圆圈.
(2)某一层上有65个圆圈,这是第 层.
(3)数图中的圆圈个数可以有多种不同的方法.
比如:前两层的圆圈个数和为(1+3)或22,
由此得,1+3=22.
同样:
由前三层的圆圈个数和得:1+3+5=32.
由前四层的圆圈个数和得:1+3+5+7=42.
…
根据上述规律,从1开始的n个连续奇数之和是多少?用n的代数式把它表示出来 .
(4)运用(3)中的规律计算:73+75+77+…+153.
18.图1为奇数排成的数表,用十字框任意框出5个数,记框内中间这个数为m,其它四个数分别记为a,b,c,d(如图2);图3为按某一规律排成的另一个数表,用十字框任意框出5个数,记框内中间这个数为n,其它四个数记为e,f,g,h(如图4).
(1)请用含m的代数式表示b.
(2)请用含n的代数式表示e.
(3)若a+b+c+d=km,e+f+g+h=pn,求k+3p的值.
19.观察图形,解答问题:
(1)按下表已填写的形式填写表中的空格:
图① 图② 图③
三个角上三个数的积 1×(﹣1)×2=﹣2 (﹣3)×(﹣4)×(﹣5)=﹣60
三个角上三个数的和 1+(﹣1)+2=2 (﹣3)+(﹣4)+(﹣5)=﹣12
积与和的商 (﹣2)÷2=﹣1
(2)请用你发现的规律求出图④中的数x和图⑤中的数y.
参考答案
1.解:由图知,
第1个图形共有小圆圈的个数为:6=2×3,
第2个图形共有小圆圈的个数为:12=3×4,
第3个图形共有小圆圈的个数为:20=4×5,
第4个图形共有小圆圈的个数为:30=5×6,
...,
第n个图形共有小圆圈的个数为:(n+1)(n+2),
∴第8个图形共有小圆圈的个数为:9×10=90,
故选:D.
2.解:根据图形的变化可知,每四个数一个正方形,且四个数在正方形上的相对位置是相同的,
∵2025÷4=506......1,
∴2025在第507个正方形右下角位置上,
故选:B.
3.解:∵当三角形内点的个数为1时,最多可以剪得3个三角形;
当三角形内点的个数为2时,最多可以剪得5个三角形;
当三角形内点的个数为3时,最多可以剪得7个三角形;
当三角形内点的个数为4时,最多可以剪得9个三角形;
∴变化规律是:三角形内的点每增加1个,最多剪得的三角形增加2个;
∴当三角形内点的个数为n时,最多可以剪得(2n+1)个三角形;
故选:C.
4.解:由图形知a1=1×2,a2=2×3,a3=3×4,
∴an=n(n+1),
∵+…+
=+++…+
=2×(1﹣+﹣+﹣+……+﹣),
=2×(1﹣)
=2×
=,
故选:A.
5.解:=,
故选:B.
6.解:∵第1个图形中苹果树的棵数是1,针叶树的棵数是8,
第2个图形中苹果树的棵数是4=22,针叶树的棵数是16=8×2,
第3个图形中苹果树的棵数是9=32,针叶树的棵数为是24=8×3,
第4个图形中苹果树的棵数为是16=42,针叶树的棵数是32=8×4,
…,
∴第n个图形中苹果树的棵数是n2,针叶树的棵数是8n,
∴当有100棵苹果树时,即n2=100,解得:n=10,
∴需要种针叶树的数量为:8×10=80(棵).
故答案为:80.
7.解:由图知,每五个数一个峰,且第奇数个峰值是正偶数,第偶数个峰值是负奇数,
故“峰7”中C的位置是7×5﹣1=34,
∵(2121﹣1)÷5=424,
∴﹣2121在E位置,
故答案为:34,E.
8.解:根据所给的图形可得:
第一个图有:5=1+1+3(个),
第二个图有:9=4+2+3(个),
第三个图有:15=9+3+3(个),
…,
则第n个为n2+n+3,
第20个图有:400+20+3=423(个),
故答案为:423.
9.解:∵四边形ABCB1为正方形,
∴AB1=AB=1,
∵A1C∥AB,
∴∠B1A1A=30°,
∴A1B1=AB1=,AA1=2AB1=2,
∵四边形A1B1C1B2为正方形,
∴A1B2=A1B1=,
∵A2C1∥A1B1,
∴∠B2A2A1=30°,
∴A2B2=A1B2=×=()2,
……
∴A2021B2021=()2021,
故答案为:()2021.
10.解:(1)由1+3=4=22,
1+3+5=9=32,
1+3+5+7=16=42,
1+3+5+7+9=25=52,
…,
∵1+3+5+7+9+…+19共有10个数,
∴1+3+5+7+9+…+19=102=100.
故答案为:100;
(2)由(1)得,1+3+5+7+9+…+(2n﹣1)=n2.
故答案为:n2.
11.解:(1)图1黑点的个数是:1;
图2黑点的个数是:3=1+(2﹣1)×2;
图3黑点的个数是:7=1+(3﹣1)×3;
…
图n黑点的个数为:1+(n﹣1) n=n2﹣n+1;
故图5中黑点的个数为:52﹣5+1=21,
故答案为:21;n2﹣n+1;
(2)当n=100时,1002﹣100+1=9901;
故答案为:9901;
(3)由题意得:n2﹣n+1=381,
解得:n=20,n=﹣19(舍去),
故答案为:20.
12.解:(1)填表:
图形序号数 ① ② ③ ④ …
地砖总数(包括黑白地砖) 2 12 30 56 …
故答案为:30,56;
(2)由图形可知:2n(2n﹣1)=4n2﹣2n,
则按照这种规律第n个图形一共用去地砖(4n2﹣2n)块.
13.解:(1)(a×b)100=a100×b100.
归纳得出:(a×b)n=an×bn.
(﹣)2021×42022=﹣()2021×42022=﹣(×4)2021×4=﹣12021×4=﹣4;
故答案为:a100×b100,an×bn,﹣4.
(2)①表中第8行的最后一个数是64,它是自然数8的平方,第8行共有15个数;
②用含n的代数式表示:第n行的第一个数是(n﹣1)2+1,最后一个数是n2,第n行共有(2n﹣1)个数.
故答案为:64,8,15;(n﹣1)2+1,n2,(2n﹣1).
14.解:(1)当高有1个立方体时,1=1,0=(1﹣1)3=03;
当高有2个立方体时,8=23,1=13=(2﹣1)3;
当高有3个立方体时,27=33,8=(3﹣1)3=23;
当高有4个立方体时,64=43,27=(4﹣1)3=33;
当高有5个立方体时,125=53,64=(5﹣1)3=43;
当高有6个立方体时,216=63,125=(6﹣1)3=53;
故答案为:125.
(2)由(1)可知,当高有n个立方体时,看不见的小立方体的个数为(n﹣1)3个.
15.解:(1)∵56=7×8,
∴数56在第7行8列;
故答案为:7;8;
(2)∵设被框住的三个数中,最大的一个数为x,则另外两个数为x﹣2,x﹣1,
∴三个数之和为x﹣2+x﹣1+x=3x﹣3.
根据题意得:3x﹣3=2019,
解得:x=674,
∵674=84×8+2,
∴数674在第85行2列,不符合题意,
∴三个数的和不可以等于2019,此时x的值为672;
3x﹣3=2019,
解得:x=674,
∵674=84×8+2,
∴数674在第85行2列,
∵方框框住相邻的三个数中最大的数x,至少位于第3列,
∴三个数的和不可以等于2019.
16.解:【规律探索】
第(1)个图形中有2=1×2张正方形纸片;
第(2)个图形中有2(1+2)=2+4=6=2×3张正方形纸片;
第(3)个图形中有2(1+2+3)=2+4+6=12=3×4张正方形纸片;
第(4)个图形中有2(1+2+3+4)=2+4+6+8=20=4×5张正方形纸片;
…
【规律归纳】
第(7)个图形中有张正方形纸片7×8=56张正方形纸片;
故答案为:56;
(2)根据上面的发现猜想:2+4+6+2n=n(n+1);
故答案为:n(n+1);
【规律应用】
①2+4+6+…+2000
=1000×1001
=1001000;
②202+204+206+…+600
=(2+4+6+…+600)﹣(2+4+6+…+200)
=300×301﹣100×101
=80200.
17.解:(1)第n层有(2n﹣1)个小圆圈;
故答案为:(2n﹣1);
(2)令2n﹣1=65,
解得n=33.
所以这是第33层;
故答案为:33;
(3)1+3+5+…+(2n﹣1)=n2;
故答案为:n2;
(4)(1+3+5+…+153)﹣(1+3+5+…+71)
=()2﹣()2
=772﹣362
=4633.
18.解:(1)由图1和图2得:b=m﹣18;
(2)如图3,分两种情况:
①当n>0时,e=﹣n+2,
②当n<0时,e=﹣n﹣2;
(3)由图1和图2得:a=m﹣2,b=m﹣18,c=m+2,d=m+18,
∵a+b+c+d=km,
∴m﹣2+m﹣18+m+2+m+18=km,
4m=km,
k=4,
由图3和图4得:分两种情况:
①当n>0时,e=﹣n+2,f=﹣n+18,g=﹣n﹣2,h=﹣n﹣18,
∵e+f+g+h=pn,
∴﹣n+2﹣n+18﹣n﹣2﹣n﹣18=pn,
﹣4n=pn,
p=﹣4,
∴k+3p=4+3×(﹣4)=﹣8.
②当n<0时,e=﹣n﹣2,f=﹣n﹣18,g=﹣n+2,h=﹣n+18,
∵e+f+g+h=pn,
∴﹣n﹣2﹣n﹣18﹣n+2﹣n+18=pn,
﹣4n=pn,
p=﹣4,
∴k+3p=4+3×(﹣4)=﹣8.
19.解:(1)图②:(﹣60)÷(﹣12)=5,
图③:(﹣2)×(﹣5)×17=170,
(﹣2)+(﹣5)+17=10,
170÷10=17.
图① 图② 图③
三个角上三个数的积 1×(﹣1)×2=﹣2 (﹣3)×(﹣4)×(﹣5)=﹣60 (﹣2)×(﹣5)×17=170
三个角上三个数的和 1+(﹣1)+2=2 (﹣3)+(﹣4)+(﹣5)=﹣12 (﹣2)+(﹣5)+17=10
积与和的商 ﹣2÷2=﹣1, (﹣60)÷(﹣12)=5, 170÷10=17
(2)图④:5×(﹣8)×(﹣9)=360,
5+(﹣8)+(﹣9)=﹣12,
x=360÷(﹣12)×2=﹣60,
图⑤:1×3×(﹣6)=﹣18,
1+3+(﹣6)=﹣2,
y=﹣18÷(﹣2)×2=18.
