2021-2022学年鲁教版(五四制)七年级数学上册第5章位置与坐标 单元综合达标测试(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)七年级数学上册第5章位置与坐标 单元综合达标测试(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 00:00:00 | ||
图片预览


文档简介
2021-2022学年鲁教版七年级数学上册《第5章位置与坐标》单元综合达标测试(附答案)
一、单选题(满分30分)
1.已知点在第四象限,且到轴的距离为,则点的坐标为( )
A. B. C. D.
2.点P的坐标为(3a-2,8-2a),若点P到两坐标轴的距离相等,则a的值是( )
A.或4 B.-2或6 C.或-4 D.2或-6
3.在平面直角坐标系中,点不可能在( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.平面直角坐标系中,已知点,,轴,线段的长是( )
A. B. C. D.
5.如图,小手盖住的点的坐标可能为( )
A.(﹣2,﹣1) B.(﹣2,1) C.(2,1) D.(2,﹣1)
6.如图,A,B的坐标为A,B(2,0),(0,1),若将线段AB平移至A1B1,点A对应点A1(3,b),点B对应点B1(a,3),则的值为( )
A.-1 B.1 C.3 D.5
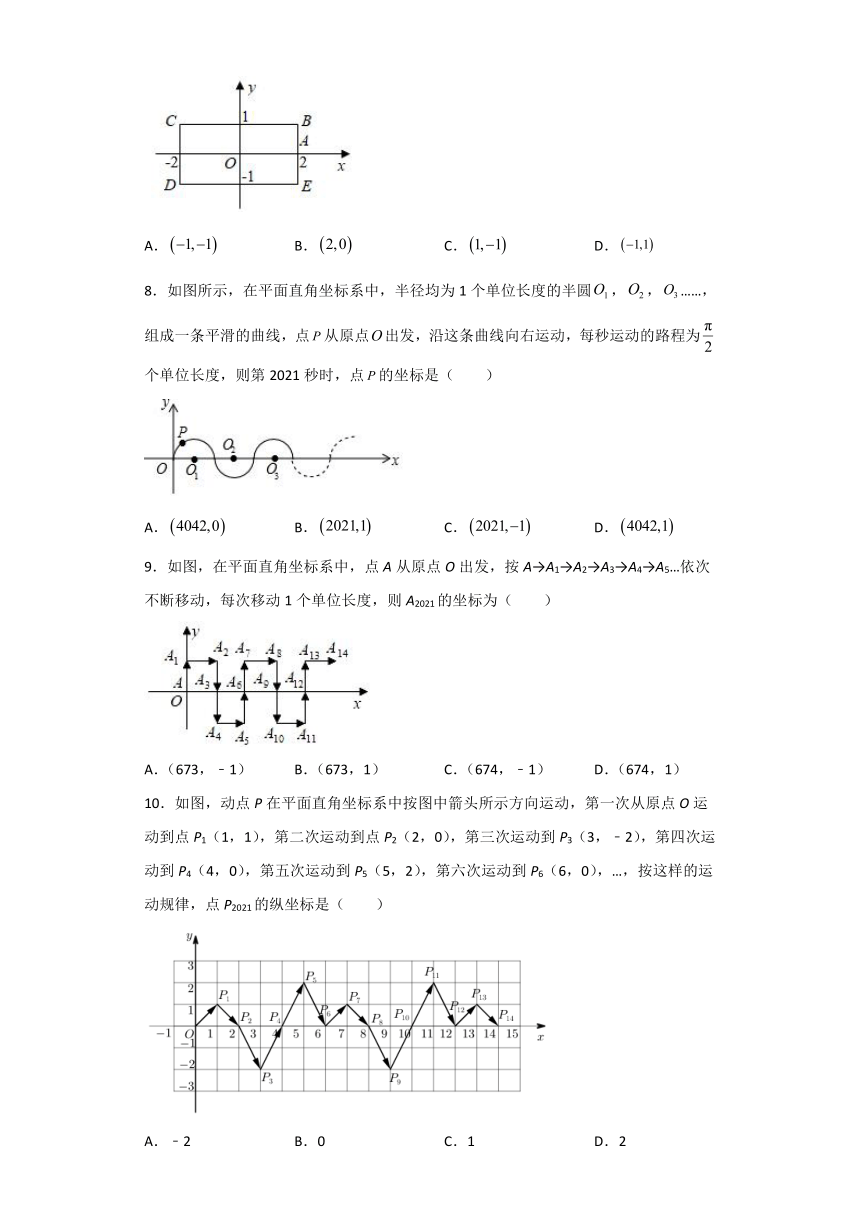
7.如图,长方形的各边分别平行于轴、轴,物体甲和物体乙由点同时出发,沿长方形的边做环绕运动,物体甲按逆时针方向以每秒1个单位长度的速度匀速运动,物体乙按顺时针方向以每秒2个单位长度的速度匀速运动则两个物体运动后的第2021次相遇地点的坐标是( )
A. B. C. D.
8.如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆,,……,组成一条平滑的曲线,点从原点出发,沿这条曲线向右运动,每秒运动的路程为个单位长度,则第2021秒时,点的坐标是( )
A. B. C. D.
9.如图,在平面直角坐标系中,点A从原点O出发,按A→A1→A2→A3→A4→A5…依次不断移动,每次移动1个单位长度,则A2021的坐标为( )
A.(673,﹣1) B.(673,1) C.(674,﹣1) D.(674,1)
10.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),第四次运动到P4(4,0),第五次运动到P5(5,2),第六次运动到P6(6,0),…,按这样的运动规律,点P2021的纵坐标是( )
A.﹣2 B.0 C.1 D.2
二、填空题(满分30分)
11.在平面直角坐标系中,点,中将线段平移得到线段,点的对应点在轴负半轴上,连接交轴于点,当时,则点的坐标为______.
12.已知,则向上平移3个单位长度,再向右平移7个单位长度后的坐标是______.
13.已知点到轴的距离是它到轴距离的,则点的坐标为__.
14.平面直角坐标系内任意一点经过向右平移5个单位再向上平移3个单位后对应点,则的值为______.
15.点P(m+2,2m+1)向右平移1个单位长度后,正好落在y轴上,则P(m+2,2m+1)在第____象限.
16.点B(﹣5,﹣2)到x轴的距离是a,到y轴的距离是b,则a+b=___.
17.在平面直角坐标系中,点,点关于x轴对称,则的值为______.
18.一只电子玩具在第一象限及x,y轴上跳动,第一次它从原点跳到(0,1),然后按图中箭头所示方向跳动(0,0)→(0,1)→(1,1)→(1,0)→……,每次跳一个单位长度,则第2021次跳到点______.
19.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次运动到点(2,0),第3次运动到点(3,﹣1),…,按照这样的运动规律,点P第2021次运动到点________.
20.如图所示,已知A1(1,0),A2(1,﹣1)、A3(﹣1,﹣1),A4(﹣1,1),A5(2,1),…,按一定规律排列,则点A2021的坐标是________.
三、解答题(满分60分)
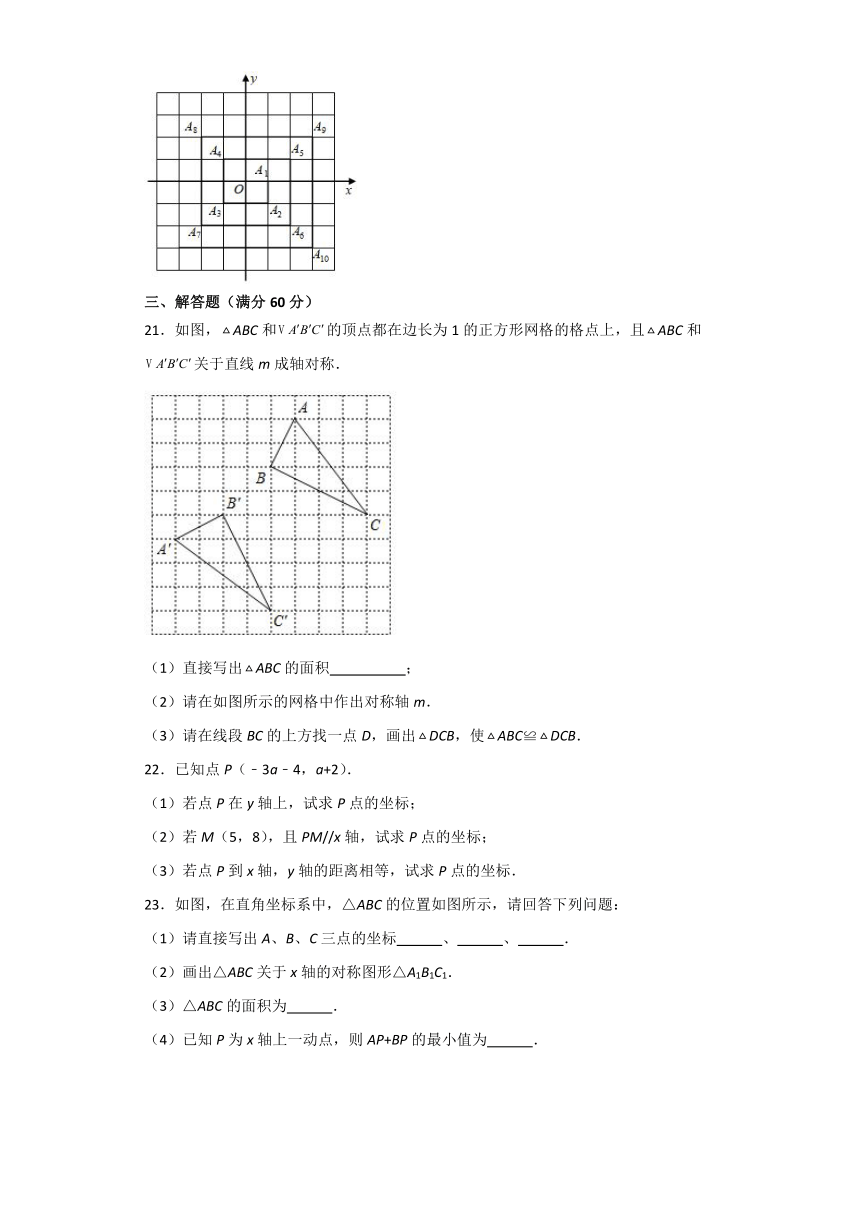
21.如图,ABC和的顶点都在边长为1的正方形网格的格点上,且ABC和关于直线m成轴对称.
(1)直接写出ABC的面积 ;
(2)请在如图所示的网格中作出对称轴m.
(3)请在线段BC的上方找一点D,画出DCB,使ABC≌DCB.
22.已知点P(﹣3a﹣4,a+2).
(1)若点P在y轴上,试求P点的坐标;
(2)若M(5,8),且PM//x轴,试求P点的坐标;
(3)若点P到x轴,y轴的距离相等,试求P点的坐标.
23.如图,在直角坐标系中,△ABC的位置如图所示,请回答下列问题:
(1)请直接写出A、B、C三点的坐标 、 、 .
(2)画出△ABC关于x轴的对称图形△A1B1C1.
(3)△ABC的面积为 .
(4)已知P为x轴上一动点,则AP+BP的最小值为 .
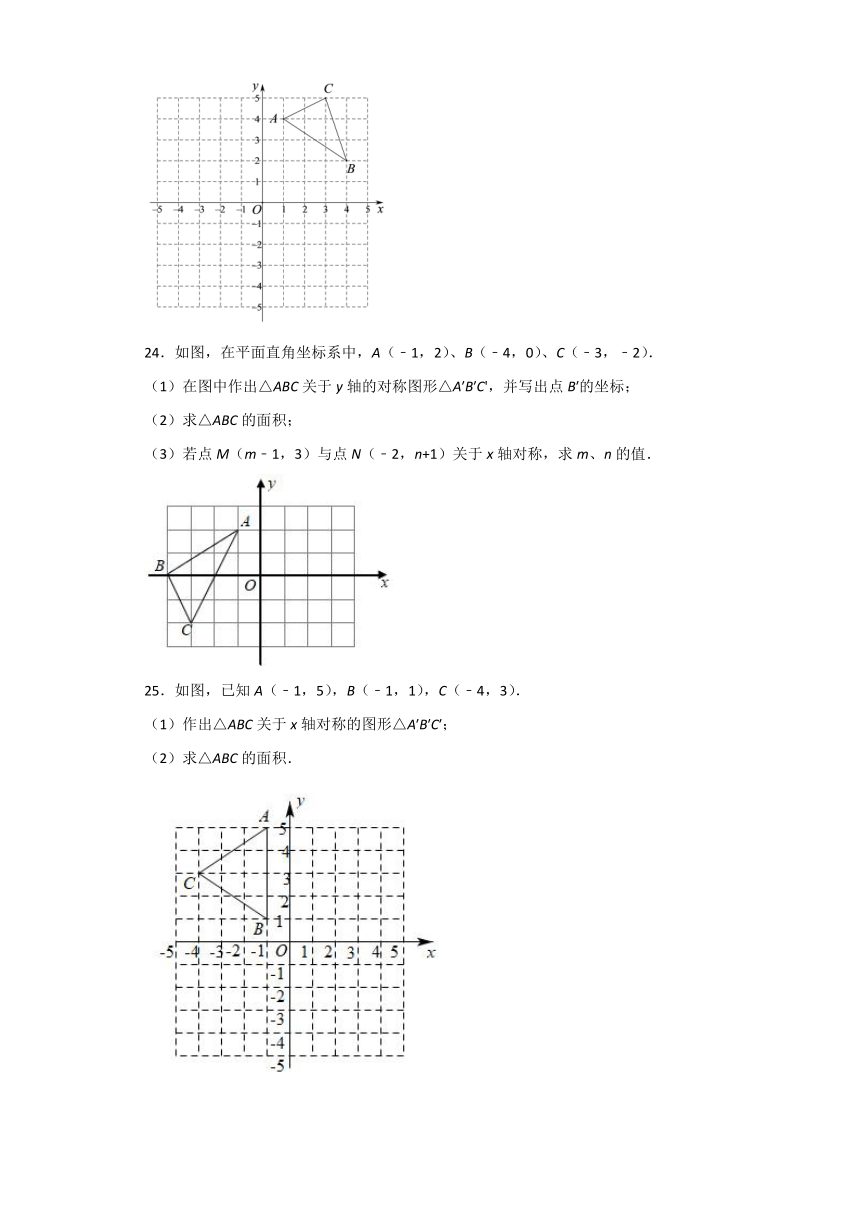
24.如图,在平面直角坐标系中,A(﹣1,2)、B(﹣4,0)、C(﹣3,﹣2).
(1)在图中作出△ABC关于y轴的对称图形△A′B′C',并写出点B′的坐标;
(2)求△ABC的面积;
(3)若点M(m﹣1,3)与点N(﹣2,n+1)关于x轴对称,求m、n的值.
25.如图,已知A(﹣1,5),B(﹣1,1),C(﹣4,3).
(1)作出△ABC关于x轴对称的图形△A′B′C′;
(2)求△ABC的面积.
26.如图,在平面直角坐标系中,直线是第一、三象限的角平分线.
实验与探究:
(1)由图观察易知关于直线的对称点的坐标为,请在图中分别标明、关于直线的对称点、的位置,并写出他们的坐标:______、______;
归纳与发现:
(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点关于第一、三象限的角平分线的对称点的坐标为_________(不必证明);
运用与拓广:
(3)已知两点、,试在直线上确定一点Q,使点Q到D、E两点的距离之和最小.
参考答案
1.A
解:∵点在第四象限,且到x轴的距离为2,
∴,
解得,
∴,
,
∴点P的坐标为(4,-2).
故选:A.
2.D
解:由题意得:,解得:或.
故选D
3.B
解:① 当时,则,,
∴此时P在第一象限;
②当时,则,,
∴此时P在第四象限;
③当时,则,,
∴此时P在第三象限;
④当时,则,,
∴此时P在y轴上;
⑤当时,则,,
∴此时P在x轴上;
∴综上所述,P不可能在第二象限,
故选B.
4.A
解:∵AB//x轴,
∴AB===
故选:A.
5.A
解:由手盖住的点在第三象限,且四个选项中仅有A(-2,-1)在第三象限.
故选A.
6.C
解:∵A,B的坐标为(2,0),(0,1)平移后点A对应点A1(3,b),点B对应点B1(a,3),
∴将线段AB向右平移1个单位,向上平移2个单位,
∴a=0+1=1,b=0+2=2,
∴a+b=1+2=3,
故选:C.
7.A
解:由已知,矩形周长为12,
∵甲、乙速度分别为1单位/秒,2单位/秒
则两个物体每次相遇时间间隔为秒,
则两个物体相遇点依次为(-1,1)、(-1,-1)、(2,0),
∵2021=3×673+2,
∴第2021次两个物体相遇位置为(-1,-1),
故选:A.
8.B
解:半径为1个单位长度的半圆的周长为×2π×1=π,
∵点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,
∴点P每秒走个半圆,
当点P从原点O出发,沿这条曲线向右运动,运动时间为1秒时,点P的坐标为(1,1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为2秒时,点P的坐标为(2,0),
当点P从原点O出发,沿这条曲线向右运动,运动时间为3秒时,点P的坐标为(3,-1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为4秒时,点P的坐标为(4,0),
当点P从原点O出发,沿这条曲线向右运动,运动时间为5秒时,点P的坐标为(5,1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为6秒时,点P的坐标为(6,0),
…,
∵2021÷4=505……1,
∴P的坐标是(2021,1),
故选:B.
9.C
解:A1(0,1),A2(1,1),A3(1,0),A4(1,﹣1),A5(2,﹣1),A6(2,0),A7(2,1),…,
点坐标运动规律可以看作每移动6次一个循环,每个循环向右移动2个单位,
则2021÷6=336…5,
所以,前336次循环运动点共向右运动336×2=672个单位,且在x轴上,
再运动5次即向右移动2个单位,向下移动一个单位,
则A2021的坐标是(674,﹣1).
故选:C.
10.D
解:观察图象,结合动点P第一次从原点O运动到点P1(1,1),
第二次运动到点P2(2,0),
第三次运动到P3(3,-2),
第四次运动到P4(4,0),
第五运动到P5(5,2),
第六次运动到P6(6,0),
…,
结合运动后的点的坐标特点,
可知由图象可得纵坐标每6次运动组成一个循环:1,0,-2,0,2,0;
∵2021÷6=336…5,
∴经过第2021次运动后,动点P的纵坐标是2,
故选:D.
11.或
解:设N(0,m),则M( 1,m+1),
设BM的解析式为y=kx+b,则有
,
解得,
∴,
如图,当H位于x轴上方时,
∵
∴,
解得:;
如图:当H位于x轴下方时,
∵
∴,
解得:,
综上:点的坐标为或,
故答案为:或.
12.(15,﹣21)
解:∵,
∴a﹣8=0,b+24=0,
∴a=8,b=﹣24,
∴(8,﹣24)向上平移3个单位长度,再向右平移7个单位长度后的坐标是(15,﹣21),
故答案为:(15,﹣21).
13.或
解:∵点,
∴点到轴的距离为:;
点到轴的距离为:;
∴,
解得:或,
∴或;
或;
∴点P为或;
故答案为:或.
14.-2
解:由题意得:a+5=c,b+3=d,
∴,
∴=,
故答案为:-2.
15.三
解:点P(m+2,2m+1)向右平移1个单位长度后,正好落在y轴上,
,
,
,
点P的坐标为(-1,-5),
故答案为:三.
16.7
解:∵点B(﹣5,﹣2)到x轴的距离是a,到y轴的距离是b,
∴a=2,b=5,
a+b=2+5=7,
故答案为:7.
17.3
解:点 与点关于轴对称,
,,
则的值是:3,
故答案为:3.
18.(3,44)
解:由题可知,电子玩具是每次跳一个单位长度,
则(0,1)用的次数是1次,即次,
(0,2)用的次数是8次,即次,
(0,3)用的次数是9次,即次,
(0,4)用的次数是24次,即次,
(0,5)用的次数是25次,即次,…
以此类推,(0,45)用的次数是2025次,即次,
2025-1-3=2021,
∴第2021次时电子玩具所在位置的坐标是(3,44).
故答案为:(3,44).
19.(2021,1)
解:第一次运动后的坐标为:(1,1),
第二次运动后的坐标为:(2,0),
第三次运动后的坐标为:(3,-1),
第四次运动后的坐标为:(4,0),
第五次运动后的坐标为:(5,1),
得出规律:点P的横坐标为运动次数,纵坐标每4次一轮,分别为1,0,-1,0;
P点的横坐标是运动次数即2021,纵坐标与第一次运动到达的点的纵坐标相同即1,
,第2021次运动后的坐标为:(2021,1),
故答案为:(2021,1).
20.(506,505)
解:根据题意得4的整数倍的各点如A4,A8,A12等点在第二象限,
∵2021÷4=505…1;
∴A2021的坐标在第一象限,
横坐标为|(2021﹣1)÷4+1|=506;纵坐标为505,
∴点A2021的坐标是(506,505).
故答案为:(506,505).
21.(1)5;(2);(3)
解:(1)的面积;
故答案是:5.
(2)如图,直线m为所作;
(3)如图,为所作;
22.(1)P(0,);(2)P(-22,8);(3)P(,)或P(-1,1).
解:(1)∵点P在y轴上,
∴,
∴,
∴
∴P(0,).
(2)∵PM//x轴,
∴,
∴,此时,,
∴P(-22,8)
(3)∵若点P到x轴,y轴的距离相等,
∴,
∴或,
解得:或,
当时,﹣3a﹣4=,a+2=,
∴P(,),
当时,﹣3a﹣4=-1,a+2=1,
∴P(-1,1),
综上所述:P(,)或P(-1,1).
23.(1);(2)见解析;(3);(4)
解:(1)由平面直角坐标系中点的位置可知
故答案为:;
(2)根据题意作的各顶点关于轴对称的点,顺次连接即可,即为所求作三角形;
(3);
(4)连接,根据,
即AP+BP的最小值为.
故答案是:
24.(1)图,点B′的坐标为(4,0);(2)4;(3)m= 1,n= 4.
解:(1)如图,△A′B′C'即为所求,点B′的坐标为(4,0);
(2)△ABC的面积为:3×4 ×2×3 ×2×4 ×1×2=12 3 4 1=4;
(3)∵点M(m 1,3)与点N( 2,n+1)关于x轴对称,
∴m 1= 2,n+1= 3,
解得m= 1,n= 4.
25.(1);(2)6
解:(1)如图所示, 即为所求;
(2)如图所示:.
26.(1),,;(2)(b,a);(3)
解:(1)B(5,3)、C(-2,5)关于直线l的对称点B′、C′的位置如图所示.
B′(3,5),C′(5,-2).
故答案为B′(3,5),C′(5,-2).
(2)由(1)可知点P(a,b)关于第一、三象限的角平分线l的对称点P′的坐标为P′(b,a).
(3)作点D关于直线l的对称点D′(-3,1),连接ED′交直线l于Q,此时QE+QD的值最小.
试卷第1页,共3页
一、单选题(满分30分)
1.已知点在第四象限,且到轴的距离为,则点的坐标为( )
A. B. C. D.
2.点P的坐标为(3a-2,8-2a),若点P到两坐标轴的距离相等,则a的值是( )
A.或4 B.-2或6 C.或-4 D.2或-6
3.在平面直角坐标系中,点不可能在( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.平面直角坐标系中,已知点,,轴,线段的长是( )
A. B. C. D.
5.如图,小手盖住的点的坐标可能为( )
A.(﹣2,﹣1) B.(﹣2,1) C.(2,1) D.(2,﹣1)
6.如图,A,B的坐标为A,B(2,0),(0,1),若将线段AB平移至A1B1,点A对应点A1(3,b),点B对应点B1(a,3),则的值为( )
A.-1 B.1 C.3 D.5
7.如图,长方形的各边分别平行于轴、轴,物体甲和物体乙由点同时出发,沿长方形的边做环绕运动,物体甲按逆时针方向以每秒1个单位长度的速度匀速运动,物体乙按顺时针方向以每秒2个单位长度的速度匀速运动则两个物体运动后的第2021次相遇地点的坐标是( )
A. B. C. D.
8.如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆,,……,组成一条平滑的曲线,点从原点出发,沿这条曲线向右运动,每秒运动的路程为个单位长度,则第2021秒时,点的坐标是( )
A. B. C. D.
9.如图,在平面直角坐标系中,点A从原点O出发,按A→A1→A2→A3→A4→A5…依次不断移动,每次移动1个单位长度,则A2021的坐标为( )
A.(673,﹣1) B.(673,1) C.(674,﹣1) D.(674,1)
10.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),第四次运动到P4(4,0),第五次运动到P5(5,2),第六次运动到P6(6,0),…,按这样的运动规律,点P2021的纵坐标是( )
A.﹣2 B.0 C.1 D.2
二、填空题(满分30分)
11.在平面直角坐标系中,点,中将线段平移得到线段,点的对应点在轴负半轴上,连接交轴于点,当时,则点的坐标为______.
12.已知,则向上平移3个单位长度,再向右平移7个单位长度后的坐标是______.
13.已知点到轴的距离是它到轴距离的,则点的坐标为__.
14.平面直角坐标系内任意一点经过向右平移5个单位再向上平移3个单位后对应点,则的值为______.
15.点P(m+2,2m+1)向右平移1个单位长度后,正好落在y轴上,则P(m+2,2m+1)在第____象限.
16.点B(﹣5,﹣2)到x轴的距离是a,到y轴的距离是b,则a+b=___.
17.在平面直角坐标系中,点,点关于x轴对称,则的值为______.
18.一只电子玩具在第一象限及x,y轴上跳动,第一次它从原点跳到(0,1),然后按图中箭头所示方向跳动(0,0)→(0,1)→(1,1)→(1,0)→……,每次跳一个单位长度,则第2021次跳到点______.
19.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次运动到点(2,0),第3次运动到点(3,﹣1),…,按照这样的运动规律,点P第2021次运动到点________.
20.如图所示,已知A1(1,0),A2(1,﹣1)、A3(﹣1,﹣1),A4(﹣1,1),A5(2,1),…,按一定规律排列,则点A2021的坐标是________.
三、解答题(满分60分)
21.如图,ABC和的顶点都在边长为1的正方形网格的格点上,且ABC和关于直线m成轴对称.
(1)直接写出ABC的面积 ;
(2)请在如图所示的网格中作出对称轴m.
(3)请在线段BC的上方找一点D,画出DCB,使ABC≌DCB.
22.已知点P(﹣3a﹣4,a+2).
(1)若点P在y轴上,试求P点的坐标;
(2)若M(5,8),且PM//x轴,试求P点的坐标;
(3)若点P到x轴,y轴的距离相等,试求P点的坐标.
23.如图,在直角坐标系中,△ABC的位置如图所示,请回答下列问题:
(1)请直接写出A、B、C三点的坐标 、 、 .
(2)画出△ABC关于x轴的对称图形△A1B1C1.
(3)△ABC的面积为 .
(4)已知P为x轴上一动点,则AP+BP的最小值为 .
24.如图,在平面直角坐标系中,A(﹣1,2)、B(﹣4,0)、C(﹣3,﹣2).
(1)在图中作出△ABC关于y轴的对称图形△A′B′C',并写出点B′的坐标;
(2)求△ABC的面积;
(3)若点M(m﹣1,3)与点N(﹣2,n+1)关于x轴对称,求m、n的值.
25.如图,已知A(﹣1,5),B(﹣1,1),C(﹣4,3).
(1)作出△ABC关于x轴对称的图形△A′B′C′;
(2)求△ABC的面积.
26.如图,在平面直角坐标系中,直线是第一、三象限的角平分线.
实验与探究:
(1)由图观察易知关于直线的对称点的坐标为,请在图中分别标明、关于直线的对称点、的位置,并写出他们的坐标:______、______;
归纳与发现:
(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点关于第一、三象限的角平分线的对称点的坐标为_________(不必证明);
运用与拓广:
(3)已知两点、,试在直线上确定一点Q,使点Q到D、E两点的距离之和最小.
参考答案
1.A
解:∵点在第四象限,且到x轴的距离为2,
∴,
解得,
∴,
,
∴点P的坐标为(4,-2).
故选:A.
2.D
解:由题意得:,解得:或.
故选D
3.B
解:① 当时,则,,
∴此时P在第一象限;
②当时,则,,
∴此时P在第四象限;
③当时,则,,
∴此时P在第三象限;
④当时,则,,
∴此时P在y轴上;
⑤当时,则,,
∴此时P在x轴上;
∴综上所述,P不可能在第二象限,
故选B.
4.A
解:∵AB//x轴,
∴AB===
故选:A.
5.A
解:由手盖住的点在第三象限,且四个选项中仅有A(-2,-1)在第三象限.
故选A.
6.C
解:∵A,B的坐标为(2,0),(0,1)平移后点A对应点A1(3,b),点B对应点B1(a,3),
∴将线段AB向右平移1个单位,向上平移2个单位,
∴a=0+1=1,b=0+2=2,
∴a+b=1+2=3,
故选:C.
7.A
解:由已知,矩形周长为12,
∵甲、乙速度分别为1单位/秒,2单位/秒
则两个物体每次相遇时间间隔为秒,
则两个物体相遇点依次为(-1,1)、(-1,-1)、(2,0),
∵2021=3×673+2,
∴第2021次两个物体相遇位置为(-1,-1),
故选:A.
8.B
解:半径为1个单位长度的半圆的周长为×2π×1=π,
∵点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,
∴点P每秒走个半圆,
当点P从原点O出发,沿这条曲线向右运动,运动时间为1秒时,点P的坐标为(1,1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为2秒时,点P的坐标为(2,0),
当点P从原点O出发,沿这条曲线向右运动,运动时间为3秒时,点P的坐标为(3,-1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为4秒时,点P的坐标为(4,0),
当点P从原点O出发,沿这条曲线向右运动,运动时间为5秒时,点P的坐标为(5,1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为6秒时,点P的坐标为(6,0),
…,
∵2021÷4=505……1,
∴P的坐标是(2021,1),
故选:B.
9.C
解:A1(0,1),A2(1,1),A3(1,0),A4(1,﹣1),A5(2,﹣1),A6(2,0),A7(2,1),…,
点坐标运动规律可以看作每移动6次一个循环,每个循环向右移动2个单位,
则2021÷6=336…5,
所以,前336次循环运动点共向右运动336×2=672个单位,且在x轴上,
再运动5次即向右移动2个单位,向下移动一个单位,
则A2021的坐标是(674,﹣1).
故选:C.
10.D
解:观察图象,结合动点P第一次从原点O运动到点P1(1,1),
第二次运动到点P2(2,0),
第三次运动到P3(3,-2),
第四次运动到P4(4,0),
第五运动到P5(5,2),
第六次运动到P6(6,0),
…,
结合运动后的点的坐标特点,
可知由图象可得纵坐标每6次运动组成一个循环:1,0,-2,0,2,0;
∵2021÷6=336…5,
∴经过第2021次运动后,动点P的纵坐标是2,
故选:D.
11.或
解:设N(0,m),则M( 1,m+1),
设BM的解析式为y=kx+b,则有
,
解得,
∴,
如图,当H位于x轴上方时,
∵
∴,
解得:;
如图:当H位于x轴下方时,
∵
∴,
解得:,
综上:点的坐标为或,
故答案为:或.
12.(15,﹣21)
解:∵,
∴a﹣8=0,b+24=0,
∴a=8,b=﹣24,
∴(8,﹣24)向上平移3个单位长度,再向右平移7个单位长度后的坐标是(15,﹣21),
故答案为:(15,﹣21).
13.或
解:∵点,
∴点到轴的距离为:;
点到轴的距离为:;
∴,
解得:或,
∴或;
或;
∴点P为或;
故答案为:或.
14.-2
解:由题意得:a+5=c,b+3=d,
∴,
∴=,
故答案为:-2.
15.三
解:点P(m+2,2m+1)向右平移1个单位长度后,正好落在y轴上,
,
,
,
点P的坐标为(-1,-5),
故答案为:三.
16.7
解:∵点B(﹣5,﹣2)到x轴的距离是a,到y轴的距离是b,
∴a=2,b=5,
a+b=2+5=7,
故答案为:7.
17.3
解:点 与点关于轴对称,
,,
则的值是:3,
故答案为:3.
18.(3,44)
解:由题可知,电子玩具是每次跳一个单位长度,
则(0,1)用的次数是1次,即次,
(0,2)用的次数是8次,即次,
(0,3)用的次数是9次,即次,
(0,4)用的次数是24次,即次,
(0,5)用的次数是25次,即次,…
以此类推,(0,45)用的次数是2025次,即次,
2025-1-3=2021,
∴第2021次时电子玩具所在位置的坐标是(3,44).
故答案为:(3,44).
19.(2021,1)
解:第一次运动后的坐标为:(1,1),
第二次运动后的坐标为:(2,0),
第三次运动后的坐标为:(3,-1),
第四次运动后的坐标为:(4,0),
第五次运动后的坐标为:(5,1),
得出规律:点P的横坐标为运动次数,纵坐标每4次一轮,分别为1,0,-1,0;
P点的横坐标是运动次数即2021,纵坐标与第一次运动到达的点的纵坐标相同即1,
,第2021次运动后的坐标为:(2021,1),
故答案为:(2021,1).
20.(506,505)
解:根据题意得4的整数倍的各点如A4,A8,A12等点在第二象限,
∵2021÷4=505…1;
∴A2021的坐标在第一象限,
横坐标为|(2021﹣1)÷4+1|=506;纵坐标为505,
∴点A2021的坐标是(506,505).
故答案为:(506,505).
21.(1)5;(2);(3)
解:(1)的面积;
故答案是:5.
(2)如图,直线m为所作;
(3)如图,为所作;
22.(1)P(0,);(2)P(-22,8);(3)P(,)或P(-1,1).
解:(1)∵点P在y轴上,
∴,
∴,
∴
∴P(0,).
(2)∵PM//x轴,
∴,
∴,此时,,
∴P(-22,8)
(3)∵若点P到x轴,y轴的距离相等,
∴,
∴或,
解得:或,
当时,﹣3a﹣4=,a+2=,
∴P(,),
当时,﹣3a﹣4=-1,a+2=1,
∴P(-1,1),
综上所述:P(,)或P(-1,1).
23.(1);(2)见解析;(3);(4)
解:(1)由平面直角坐标系中点的位置可知
故答案为:;
(2)根据题意作的各顶点关于轴对称的点,顺次连接即可,即为所求作三角形;
(3);
(4)连接,根据,
即AP+BP的最小值为.
故答案是:
24.(1)图,点B′的坐标为(4,0);(2)4;(3)m= 1,n= 4.
解:(1)如图,△A′B′C'即为所求,点B′的坐标为(4,0);
(2)△ABC的面积为:3×4 ×2×3 ×2×4 ×1×2=12 3 4 1=4;
(3)∵点M(m 1,3)与点N( 2,n+1)关于x轴对称,
∴m 1= 2,n+1= 3,
解得m= 1,n= 4.
25.(1);(2)6
解:(1)如图所示, 即为所求;
(2)如图所示:.
26.(1),,;(2)(b,a);(3)
解:(1)B(5,3)、C(-2,5)关于直线l的对称点B′、C′的位置如图所示.
B′(3,5),C′(5,-2).
故答案为B′(3,5),C′(5,-2).
(2)由(1)可知点P(a,b)关于第一、三象限的角平分线l的对称点P′的坐标为P′(b,a).
(3)作点D关于直线l的对称点D′(-3,1),连接ED′交直线l于Q,此时QE+QD的值最小.
试卷第1页,共3页
