4.4.3不同函数增长的差异课件-2021-2022学年高一上学期数学人教A版(2019)必修第一册(24张PPT)
文档属性
| 名称 | 4.4.3不同函数增长的差异课件-2021-2022学年高一上学期数学人教A版(2019)必修第一册(24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 872.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 21:34:38 | ||
图片预览






文档简介
(共24张PPT)
4.4.3
不同函数的增长差异
高一数学必修第一册 第四章 指数函数和对数函数
理解直线上升、指数爆炸、对数增长
的含义;
2.区分指数函数、对数函数以及一次函数增长的差异;
3.会选择适当的函数模型分析和解决一些实际问题.
4.核心素养:数学建模、逻辑推理、数学运算.
学习目标
生态故事:“一群兔子引发的危机”
有一大群喝水、嬉戏的兔子,但是这群兔子曾使澳大利亚伤透了脑筋.1859年,有人从欧洲带进澳洲几只兔子,由于澳洲有茂盛的牧草,而且没有兔子的天敌,兔子数量不断增加,不到100年,兔子们占领了整个澳大利亚,数量达到75亿只.可爱的兔子变得可恶起来,75亿只兔子吃掉了相当于75亿只羊所吃的牧草,草原的载畜率大大降低,而牛羊是澳大利亚的主要牲口.这使澳大利亚头痛不已,他们采用各种方法消灭这些兔子,直至二十世纪五十年代,科学家采用载液瘤病毒杀死了百分之九十的野兔,澳大利亚人才算松了一口气.
材料:澳大利亚兔子数“爆炸”
x
y
o
x
y
o
1
(a > 1)
x
o
y
1
(a > 1)
x
x
y
o
y=x3
x
y
o
一、回顾基本函数的图象
x
y
o
>
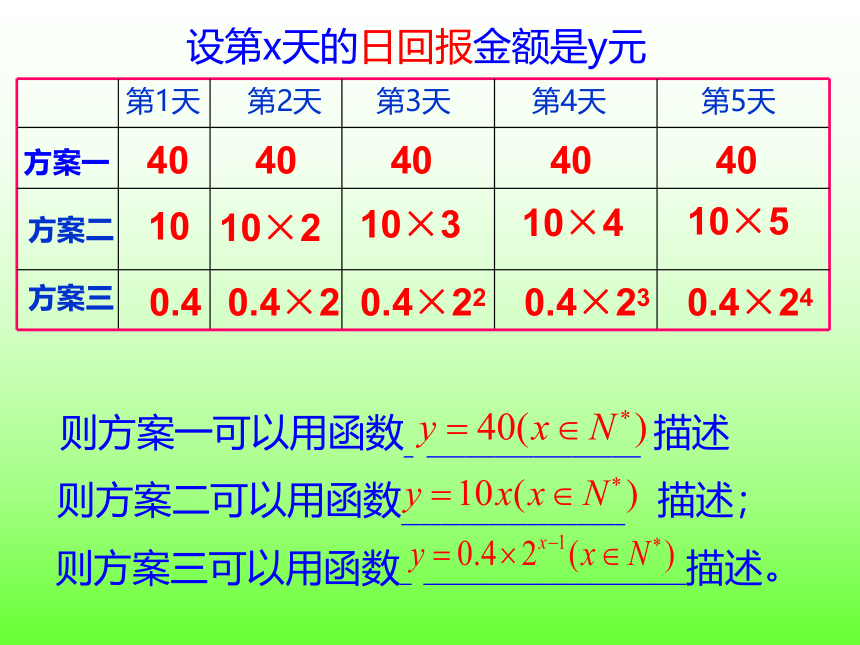
1.例1.假如你有一笔资金用于投资,现有三种方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番.
请问,你会选择哪种投资方案?
回报量
日回报量
累计回报量
选择投资方案
的标准
二、探究不同函数增长的差异
设第x天的日回报金额是y元
则方案一可以用函数_ ______________________ 描述
则方案二可以用函数_______________________ 描述;
则方案三可以用函数_ ______________________描述。
方案一
方案二
方案三
第1天
第3天
第2天
第4天
第5天
40
40
40
40
40
10
10×2
10×3
10×4
10×5
0.4
0.4×2
0.4×22
0.4×23
0.4×24
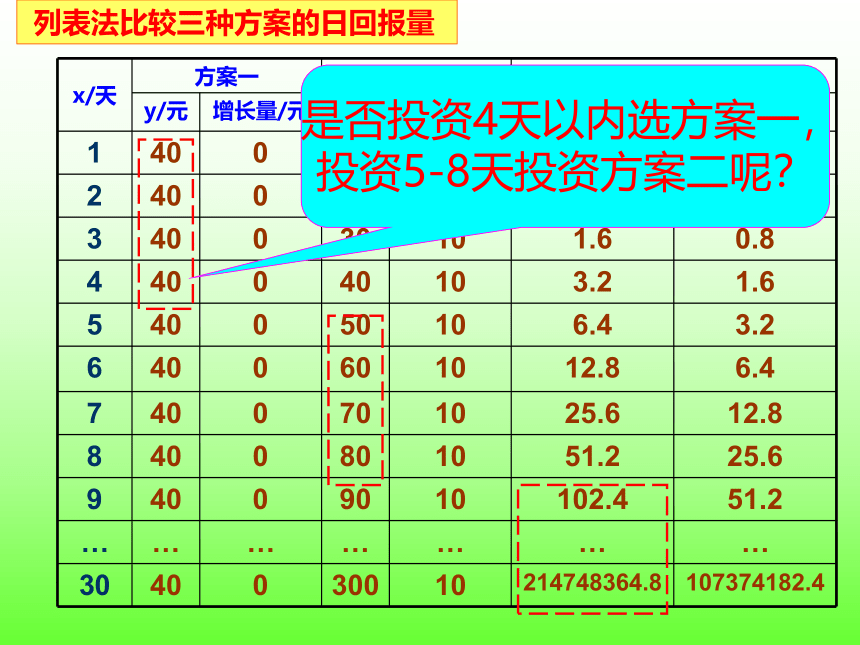
x/天 方案一 方案二 方案三
y/元 增长量/元 y/元 增长量/元 y/元 增长量/元
1 40 0 10 0.4
2 40 0 20 10 0.8 0.4
3 40 0 30 10 1.6 0.8
4 40 0 40 10 3.2 1.6
5 40 0 50 10 6.4 3.2
6 40 0 60 10 12.8 6.4
7 40 0 70 10 25.6 12.8
8 40 0 80 10 51.2 25.6
9 40 0 90 10 102.4 51.2
… … … … … … …
30 40 0 300 10 214748364.8 107374182.4
是否投资4天以内选方案一,
投资5-8天投资方案二呢?
列表法比较三种方案的日回报量
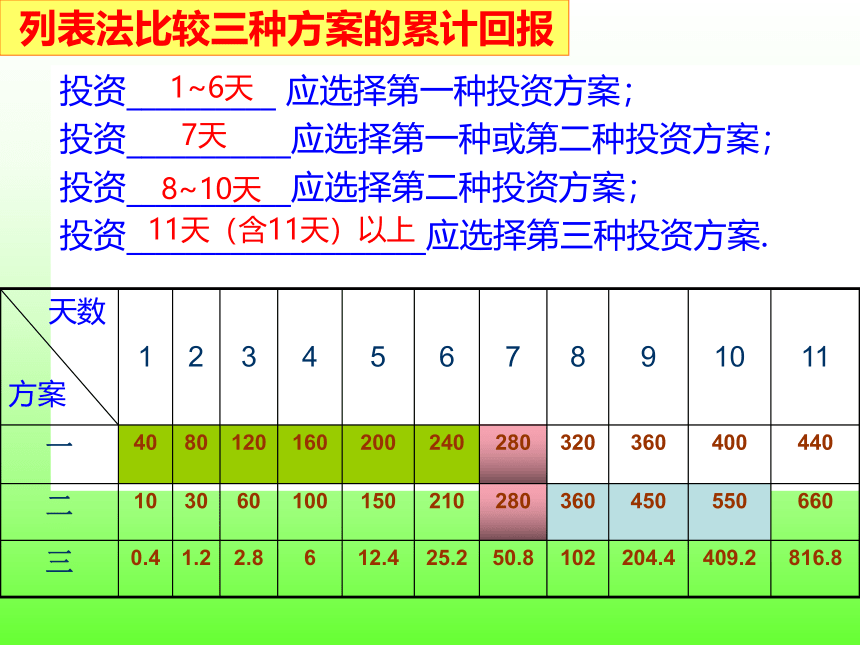
投资__________ 应选择第一种投资方案;
投资___________应选择第一种或第二种投资方案;
投资___________应选择第二种投资方案;
投资____________________应选择第三种投资方案.
1~6天
7天
列表法比较三种方案的累计回报
8~10天
11天(含11天)以上
天数
方案 1 2 3 4 5 6 7 8 9 10 11
一 40 80 120 160 200 240 280 320 360 400 440
二 10 30 60 100 150 210 280 360 450 550 660
三 0.4 1.2 2.8 6 12.4 25.2 50.8 102 204.4 409.2 816.8
匀速增长
急剧增长
没有增长
比较函数的增长差异?
2.探究:函数 的增长情况并分析差异
0 1 0
0.5 1.414 1
1 2 2
1.5 2.828 3
2 4 4
2.5 5.657 5
3 8 6
··· ··· ···
2
3
4
5
6
7
8
1
2
3
1
o
这两个函数在[0,+∞)上单调递增,但它们的增长速度不同,函数y=2x的增长速度保持不变,而函数y=2x的增长速度在变化.
2.探究:在更大的范围内观察函数 的增长情况
0 1 0
2 4 4
4 16 8
6 64 12
8 256 16
10 1240 20
12 4096 24
··· ··· ···
200
400
600
800
5
10
15
o
当自变量x越来越大时,y=2x的图象就像与x轴垂直的一样,2x的值快速增长,而函数y=2x的增长速度依然保持不变,而与函数y=2x的增长速度相比几乎微不足道.
3.通过以上探究可以发现:
一般地,对于指数函数y=ax (a>1)和一次函数y=kx (k>0)增长的差异为:
在区间(0,+∞)上都单调递增,但它们增长速度不同,无论k比a大多少,尽管在x的一定范围内,ax会小kx,但随着x的增大一次函数y=kx (k>0)保持固定的增长速度,而指数函数y=ax (a>1)快速增长,因此ax的增长快于kx的增长,那么总存在一个x0,当x>x0时,恒有ax>kx.因此,指数函数的增长会越来越快,呈爆炸性增长.
4.探究:在区间[0,+∞)函数 的增长差异及对数函数的增长特点
0 不存在 0
10 1 1
20 1.301 2
30 1.477 3
40 1.602 4
50 1.699 5
60 1.778 6
··· ··· ···
1
2
3
4
10
20
40
o
5
6
30
50
60
这两个函数在[0,+∞)上单调递增,但它们的增长速度不同,函数 的增长速度保持不变,而函数y=lgx的增长速度在变化,增长的速度较慢.
一般地,对于指数函数y=logax (a>1)和一次
函数y=kx (k>0)的增长差异为:
在区间(0,+∞)上都单调递增,但它们的增长速度不同,随着x的增大,一次函数y=kx (k>0)保持固定的增长速度,而对数函数y= logax (a>1)增大得越来越慢,图象就像是渐渐地与x轴平行一样.尽管在x的一定范围内, logax可能会大于kx,但由于logax的增长慢于kx的增长,因此总存在一个x0,当x>x0时,就会有logax5.通过以上探究可以发现:
6.例2、某公司2009年为了实现1000万元总利润的目标,他准备制定一个激励销售部门的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随着销售利润x (单位:万元)的增加而增加,但奖金数不超过5万元,同时奖金不超过利润的25%.现有三个奖励模型:
y=0.25x,y=log7x+1,y=1.002x,
其中哪个模型能符合公司的要求呢?
1.函数变量x,y满足什么条件才算符合公司要求?
2.根据函数图象讨论哪个函数符合条件?
400
600
800
1000
200
1
2
3
4
5
6
7
8
x
y
o
y=0.25x
根据函数图象讨论哪个函数符合条件
400
600
800
1000
200
1
2
3
4
5
6
7
8
x
y
o
指数爆炸
y=0.25x
观察图象比较三种函数的增长情况
直线上升
对数平稳
7总结三种函数的增长的差异
(1).在区间(0,+∞)上,y=ax (a>1),y=logax (a>1)
和y=kx (k>0)都是增函数.
(2).随着x的增大, y=ax (a>1)的增长速度越来越
快,会远远大于y=kx (k>0)的增长速度.
(3).随着x的增大, y=logax (a>1)的增长速度越来
越慢,会远远小于y=kx (k>0)的增长速度.
总存在一个x0,当x>x0时,就有
logax1).四个变量y1,y2,y3,y4随变量x变化的数据如下
关于x成指数型变化的变量是_______
y2
1.005
1.0151
1.0461
1.1407
1.4295
2.3107
5
155
130
105
80
55
30
5
33733
1758.2
94.478
5
4505
3130
2005
1130
505
130
5
30
25
20
15
10
5
0
8巩固练习
2).当x越来越大时,增长速度最快的是( )
D
4).趣味游戏一张纸的厚度大约为0.01cm,请计算将一张纸对折n次的厚度.
3).观察下表,某人身高用一次函数、指数型函数、对数型函数哪个刻画比较好,为什么?
世界最高峰——珠峰海拔高度最新测量结果8844.43米,请问对折几次即可超过珠峰高度?
某人的年龄和身高
年龄
身高
21
23
25
27
160
162
163
163.5
1.几种常见函数的增长差异:
没有增长
直线上升
指数爆炸
缓慢增长
2.解决实际问题的步骤:
实际问题
读懂问题
抽象概括
数学问题
数学问题的解
还原说明
实际问题的解
演算
推理
常数函数
一次函数
指数函数
对数函数
三、课堂小结
作业: 课本P141 习题4.4 11题
4.4.3
不同函数的增长差异
高一数学必修第一册 第四章 指数函数和对数函数
理解直线上升、指数爆炸、对数增长
的含义;
2.区分指数函数、对数函数以及一次函数增长的差异;
3.会选择适当的函数模型分析和解决一些实际问题.
4.核心素养:数学建模、逻辑推理、数学运算.
学习目标
生态故事:“一群兔子引发的危机”
有一大群喝水、嬉戏的兔子,但是这群兔子曾使澳大利亚伤透了脑筋.1859年,有人从欧洲带进澳洲几只兔子,由于澳洲有茂盛的牧草,而且没有兔子的天敌,兔子数量不断增加,不到100年,兔子们占领了整个澳大利亚,数量达到75亿只.可爱的兔子变得可恶起来,75亿只兔子吃掉了相当于75亿只羊所吃的牧草,草原的载畜率大大降低,而牛羊是澳大利亚的主要牲口.这使澳大利亚头痛不已,他们采用各种方法消灭这些兔子,直至二十世纪五十年代,科学家采用载液瘤病毒杀死了百分之九十的野兔,澳大利亚人才算松了一口气.
材料:澳大利亚兔子数“爆炸”
x
y
o
x
y
o
1
(a > 1)
x
o
y
1
(a > 1)
x
x
y
o
y=x3
x
y
o
一、回顾基本函数的图象
x
y
o
>
1.例1.假如你有一笔资金用于投资,现有三种方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番.
请问,你会选择哪种投资方案?
回报量
日回报量
累计回报量
选择投资方案
的标准
二、探究不同函数增长的差异
设第x天的日回报金额是y元
则方案一可以用函数_ ______________________ 描述
则方案二可以用函数_______________________ 描述;
则方案三可以用函数_ ______________________描述。
方案一
方案二
方案三
第1天
第3天
第2天
第4天
第5天
40
40
40
40
40
10
10×2
10×3
10×4
10×5
0.4
0.4×2
0.4×22
0.4×23
0.4×24
x/天 方案一 方案二 方案三
y/元 增长量/元 y/元 增长量/元 y/元 增长量/元
1 40 0 10 0.4
2 40 0 20 10 0.8 0.4
3 40 0 30 10 1.6 0.8
4 40 0 40 10 3.2 1.6
5 40 0 50 10 6.4 3.2
6 40 0 60 10 12.8 6.4
7 40 0 70 10 25.6 12.8
8 40 0 80 10 51.2 25.6
9 40 0 90 10 102.4 51.2
… … … … … … …
30 40 0 300 10 214748364.8 107374182.4
是否投资4天以内选方案一,
投资5-8天投资方案二呢?
列表法比较三种方案的日回报量
投资__________ 应选择第一种投资方案;
投资___________应选择第一种或第二种投资方案;
投资___________应选择第二种投资方案;
投资____________________应选择第三种投资方案.
1~6天
7天
列表法比较三种方案的累计回报
8~10天
11天(含11天)以上
天数
方案 1 2 3 4 5 6 7 8 9 10 11
一 40 80 120 160 200 240 280 320 360 400 440
二 10 30 60 100 150 210 280 360 450 550 660
三 0.4 1.2 2.8 6 12.4 25.2 50.8 102 204.4 409.2 816.8
匀速增长
急剧增长
没有增长
比较函数的增长差异?
2.探究:函数 的增长情况并分析差异
0 1 0
0.5 1.414 1
1 2 2
1.5 2.828 3
2 4 4
2.5 5.657 5
3 8 6
··· ··· ···
2
3
4
5
6
7
8
1
2
3
1
o
这两个函数在[0,+∞)上单调递增,但它们的增长速度不同,函数y=2x的增长速度保持不变,而函数y=2x的增长速度在变化.
2.探究:在更大的范围内观察函数 的增长情况
0 1 0
2 4 4
4 16 8
6 64 12
8 256 16
10 1240 20
12 4096 24
··· ··· ···
200
400
600
800
5
10
15
o
当自变量x越来越大时,y=2x的图象就像与x轴垂直的一样,2x的值快速增长,而函数y=2x的增长速度依然保持不变,而与函数y=2x的增长速度相比几乎微不足道.
3.通过以上探究可以发现:
一般地,对于指数函数y=ax (a>1)和一次函数y=kx (k>0)增长的差异为:
在区间(0,+∞)上都单调递增,但它们增长速度不同,无论k比a大多少,尽管在x的一定范围内,ax会小kx,但随着x的增大一次函数y=kx (k>0)保持固定的增长速度,而指数函数y=ax (a>1)快速增长,因此ax的增长快于kx的增长,那么总存在一个x0,当x>x0时,恒有ax>kx.因此,指数函数的增长会越来越快,呈爆炸性增长.
4.探究:在区间[0,+∞)函数 的增长差异及对数函数的增长特点
0 不存在 0
10 1 1
20 1.301 2
30 1.477 3
40 1.602 4
50 1.699 5
60 1.778 6
··· ··· ···
1
2
3
4
10
20
40
o
5
6
30
50
60
这两个函数在[0,+∞)上单调递增,但它们的增长速度不同,函数 的增长速度保持不变,而函数y=lgx的增长速度在变化,增长的速度较慢.
一般地,对于指数函数y=logax (a>1)和一次
函数y=kx (k>0)的增长差异为:
在区间(0,+∞)上都单调递增,但它们的增长速度不同,随着x的增大,一次函数y=kx (k>0)保持固定的增长速度,而对数函数y= logax (a>1)增大得越来越慢,图象就像是渐渐地与x轴平行一样.尽管在x的一定范围内, logax可能会大于kx,但由于logax的增长慢于kx的增长,因此总存在一个x0,当x>x0时,就会有logax
6.例2、某公司2009年为了实现1000万元总利润的目标,他准备制定一个激励销售部门的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随着销售利润x (单位:万元)的增加而增加,但奖金数不超过5万元,同时奖金不超过利润的25%.现有三个奖励模型:
y=0.25x,y=log7x+1,y=1.002x,
其中哪个模型能符合公司的要求呢?
1.函数变量x,y满足什么条件才算符合公司要求?
2.根据函数图象讨论哪个函数符合条件?
400
600
800
1000
200
1
2
3
4
5
6
7
8
x
y
o
y=0.25x
根据函数图象讨论哪个函数符合条件
400
600
800
1000
200
1
2
3
4
5
6
7
8
x
y
o
指数爆炸
y=0.25x
观察图象比较三种函数的增长情况
直线上升
对数平稳
7总结三种函数的增长的差异
(1).在区间(0,+∞)上,y=ax (a>1),y=logax (a>1)
和y=kx (k>0)都是增函数.
(2).随着x的增大, y=ax (a>1)的增长速度越来越
快,会远远大于y=kx (k>0)的增长速度.
(3).随着x的增大, y=logax (a>1)的增长速度越来
越慢,会远远小于y=kx (k>0)的增长速度.
总存在一个x0,当x>x0时,就有
logax
关于x成指数型变化的变量是_______
y2
1.005
1.0151
1.0461
1.1407
1.4295
2.3107
5
155
130
105
80
55
30
5
33733
1758.2
94.478
5
4505
3130
2005
1130
505
130
5
30
25
20
15
10
5
0
8巩固练习
2).当x越来越大时,增长速度最快的是( )
D
4).趣味游戏一张纸的厚度大约为0.01cm,请计算将一张纸对折n次的厚度.
3).观察下表,某人身高用一次函数、指数型函数、对数型函数哪个刻画比较好,为什么?
世界最高峰——珠峰海拔高度最新测量结果8844.43米,请问对折几次即可超过珠峰高度?
某人的年龄和身高
年龄
身高
21
23
25
27
160
162
163
163.5
1.几种常见函数的增长差异:
没有增长
直线上升
指数爆炸
缓慢增长
2.解决实际问题的步骤:
实际问题
读懂问题
抽象概括
数学问题
数学问题的解
还原说明
实际问题的解
演算
推理
常数函数
一次函数
指数函数
对数函数
三、课堂小结
作业: 课本P141 习题4.4 11题
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
