4.4.3不同函数增长的差异 课件-2021-2022学年高一上学期数学人教A版(2019)必修第一册(20张PPT)
文档属性
| 名称 | 4.4.3不同函数增长的差异 课件-2021-2022学年高一上学期数学人教A版(2019)必修第一册(20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 21:42:35 | ||
图片预览








文档简介
(共20张PPT)
4.4.3 不同函数增长的差异
| 常见函数模型的比较
y=ax(a>1) y=logax(a>1) y=kx(k>0)
在(0,+∞) 上的增减性 ① 单调递增 ② 单调递增 ③ 单调递增
图象的变化 随x的增大逐渐变“陡” 随x的增大逐渐变“缓” 增长速度不变
增长速度 y=ax(a>1)的增长速度远远④ 快于 y=kx(k>0)的增长速度,y=kx(k>0)的增
长速度⑤ 快于 y=logax(a>1)的增长速度
结果 存在一个x0,当x>x0时,有⑥ ax>kx>logax
1.当x每增加一个单位时,y增加或减少的量为定值(不为0),则y是x的一次函数.
( √ )
2. 函数y=x2比y=2x增长的速度更快些. ( )
3.不存在一个实数m,使得当x>m时,1.1x>x100. ( )
提示:由于底数大于1的指数函数增长速度大于幂函数,因此存在一个实数m,使得
当x>m时,1.1x>x100.
4.对数函数y=logax(a>1)和幂函数y=xn(n>0)在区间(0,+∞)上,总存在一个x0,当x>x0
时,有logax5.在函数y=3x,y=log3x,y=3x,y=x3中,增长速度最快的是y=3x. ( √ )
提示:在这几类函数中,指数函数的增长速度最快.
判断正误,正确的画“ √” ,错误的画“ ” .
1 | 几类函数模型增长的差异
假如某公司每天向你投资1万元,共投资30天.该公司要求你给他的回报是第
一天给公司1分钱,第二天给公司2分钱,以后每天给的钱都是前一天的2倍,共30天.
问题
1.你认为这样的交易对你有利吗
提示:公司给你的总投资为30万元;
你给公司的回报为 0.01+0.01×2+0.01×22+…+0.01×229=10 737 418.23≈1 074(万
元).
由此可见,这样的交易对你没有利.
2.上述问题中,你发现了什么问题
提示:函数y=ax(a>1)与y=kx(k>0)都是增函数,随着x的增大,指数函数的增长速度越
来越快,相比指数函数,一次函数增长得较慢.
常见的函数模型及增长特点
1.线性函数模型y=kx+b(k>0)的增长特点是增长速度不变,可称为“直线上升”.
2.指数函数模型y=ax(a>1)的增长特点是随着自变量的增大,函数值增大的速度越
来越快,即增长速度急剧,形象地称为“指数爆炸”.
3.对数函数模型y=logax(a>1)的增长特点是随着自变量的增大,函数值增大的速度
越来越慢,即增长速度平缓,可称为“对数增长”.
甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程fi(x)
(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为f1(x)=2x-1, f2(x)=x2, f3(x)=x, f4(x)=
log2(x+1),有以下结论:
①当x>1时,甲在最前面;
②当x>1时,乙在最前面;
③当01时,丁在最后面;
④丙不可能在最前面,也不可能在最后面;
⑤如果它们一直运动下去,那么最终在最前面的是甲.
其中,所有正确结论的序号为 ③④⑤ .
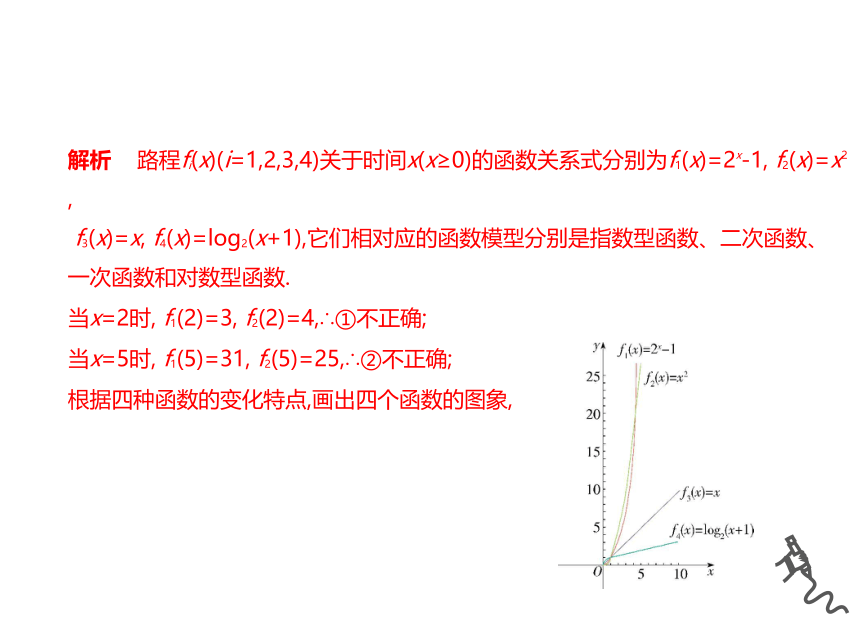
解析 路程fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为f1(x)=2x-1, f2(x)=x2,
f3(x)=x, f4(x)=log2(x+1),它们相对应的函数模型分别是指数型函数、二次函数、
一次函数和对数型函数.
当x=2时, f1(2)=3, f2(2)=4,∴①不正确;
当x=5时, f1(5)=31, f2(5)=25,∴②不正确;
根据四种函数的变化特点,画出四个函数的图象,
可知当x=1时,甲、乙、丙、丁四个物体的路程相等,而对数型函数的增长速度是
先快后慢,从而当01时,丁在最后面,∴③正确;
结合各函数图象的变化情况,可知丙不可能在最前面,也不可能在最后面,∴④正
确;
指数函数的增长速度急剧,故若运动的时间足够长,则最前面的物体一定是按照
指数型函数运动的物体,即一定是甲,∴⑤正确.
2 | 几种常见的函数模型的选择
不同的函数模型能刻画现实世界中不同的变化规律:
(1)线性函数模型适合描述增长速度不变的变化规律;
(2)指数函数模型适合描述增长速度急剧的变化规律;
(3)对数函数、幂函数模型适合描述增长速度平缓的变化规律.
因此,需抓住题中蕴含的数学信息,恰当、准确地建立相应变化规律的函数模型
来解决实际问题.
某皮鞋厂今年1月份开始投产,并且前4个月的产量分别为1万双,1.2万双,1.3
万双,1.37万双.由于产品质量好、款式新颖,前几个月的销售情况良好.为了推销
员在推销产品时接受订单不至于过多或过少,需要估计以后几个月的产量,且厂
里暂时不准备增加设备和工人.假如你是厂长,就月份为x,产量为y给出三种函数
模型:y=ax+b,y=ax2+bx+c,y=abx+c,其中a≠0,你将利用哪一种模型去估算以后几个
月的产量
解析 由题意知,将产量随时间变化的数据分别表示为A(1,1),B(2,1.2),C(3,1.3),
D(4,1.37).
(1)若选择函数y=ax+b,
将B,C两点的坐标代入函数解析式,
得 解得
∴y=0.1x+1.
由此可得结论:在不增加工人和设备的条件下,产量会每月增加1 000双,这是不太
可能的.
(2)若选择函数y=ax2+bx+c,将A,B,C三点的坐标代入函数解析式,
得
解得
∴y=-0.05x2+0.35x+0.7.
由此式计算得4月份的产量为1.3万双,比实际产量少700双,而且由二次函数的性
质可知,产量自4月份开始每月下降,不符合实际.
(3)若选择函数y=abx+c,
将A,B,C三点的坐标代入函数解析式,
得
由①得ab=1-c,代入②③,
得 解得
则a= =-0.8,
∴y=-0.8×0.5x+1.4.
把x=4代入,得y=-0.8×0.54+1.4=1.35.故在三个函数模型中y=abx+c的误差最小.
随着工人技术和管理效益逐渐提高,一段时间内产量会明显上升,但经过一段时
间之后,如果不增加设备和工人,产量必然趋于稳定,而y=-0.8×0.5x+1.4恰好反映了
这种趋势.
因此选用函数模型y=-0.8×0.5x+1.4比较接近客观实际.
题组一 不同函数增长的差异
1.下列函数中,增长速度越来越慢的是 ( B )
A.y=6x B.y=log6x C.y=x6 D.y=6x
2.某校甲、乙两食堂某年1月份的营业额相等,甲食堂的营业额逐月增加,并且每月的增加值相同;乙食堂的营业额也逐月增加,且每月增加的百分率相同.已知同年9月份两食堂的营业额又相等,则同年5月份 ( A )
A.甲食堂的营业额较高 B.乙食堂的营业额较高
C.甲、乙两食堂的营业额相同 D.不能确定甲、乙哪个食堂的营业额较高
3.(2020湖南醴陵一中高一上期中)已知函数y1=2x,y2=x2,y3=log2x,在区间(0,+∞)上一定存在x0,当x>x0时( A )
A.2x>x2>log2x B.x2>2x>log2x C.log2x>2x>x2 D.log2x>x2>2x
4.某小型贸易公司为了实现年终10万元利润的目标,特制订了一个销售人员年终绩效奖励方案:当销售利润为x万元(4≤x≤10)时,奖金y(万元)随销售利润x(万元)的增加而增加,但奖金总数不超过2万元,同时不超过销售利润的,则下列函数中,符合该公司奖励方案的函数模型是(参考数据:lg 2≈0.3,lg 3≈0.48,lg 5≈0.7) ( B )
A.y=0.4x B.y=lg x+1 C.y= D.y=1.125x
题组二 图象信息迁移问题
5.向高为H的水瓶内注水,一直到注满为止,如果注水量V与水深h的函数图象如图所示,那么水瓶的形状大致是 ( B )
6.(2021山东德州、烟台高一上期中联考)某高三学生于2020年9月第二个周末乘高铁赴济南参加全国高中数学联赛(山东省赛区)的比赛活动.早上他乘坐出租车从家里出发,离开家不久,发现身份证忘在家里了,于是回到家取上身份证,然后乘坐出租车以更快的速度赶往高铁站,令x(单位:分钟)表示他离开家的时间,y(单位:千米)表示离开家的距离,其中等待红绿灯及在家取身份证的时间忽略不计,出租车匀速行驶,则下列图象中与上述事件吻合最好的是 ( C )
7.(多选)如图所示的是某受污染的湖泊在自然净化的过程中某种有害物质的剩余量y与净化时间t(月)之间满足的函数关系:y=at(t≥0,a>0,a≠1)的图象.若有害物质的初始量为1,则以下说法中正确的是 ( ACD) )
A.第4个月时,剩余量就会低于
B.每月减少的有害物质的量都相等
C.有害物质每月的衰减率为
D.当剩余量为,, 时,所经过的时间分别是t1,t2,t3,则t1+t2=t3
C
4.4.3 不同函数增长的差异
| 常见函数模型的比较
y=ax(a>1) y=logax(a>1) y=kx(k>0)
在(0,+∞) 上的增减性 ① 单调递增 ② 单调递增 ③ 单调递增
图象的变化 随x的增大逐渐变“陡” 随x的增大逐渐变“缓” 增长速度不变
增长速度 y=ax(a>1)的增长速度远远④ 快于 y=kx(k>0)的增长速度,y=kx(k>0)的增
长速度⑤ 快于 y=logax(a>1)的增长速度
结果 存在一个x0,当x>x0时,有⑥ ax>kx>logax
1.当x每增加一个单位时,y增加或减少的量为定值(不为0),则y是x的一次函数.
( √ )
2. 函数y=x2比y=2x增长的速度更快些. ( )
3.不存在一个实数m,使得当x>m时,1.1x>x100. ( )
提示:由于底数大于1的指数函数增长速度大于幂函数,因此存在一个实数m,使得
当x>m时,1.1x>x100.
4.对数函数y=logax(a>1)和幂函数y=xn(n>0)在区间(0,+∞)上,总存在一个x0,当x>x0
时,有logax
提示:在这几类函数中,指数函数的增长速度最快.
判断正误,正确的画“ √” ,错误的画“ ” .
1 | 几类函数模型增长的差异
假如某公司每天向你投资1万元,共投资30天.该公司要求你给他的回报是第
一天给公司1分钱,第二天给公司2分钱,以后每天给的钱都是前一天的2倍,共30天.
问题
1.你认为这样的交易对你有利吗
提示:公司给你的总投资为30万元;
你给公司的回报为 0.01+0.01×2+0.01×22+…+0.01×229=10 737 418.23≈1 074(万
元).
由此可见,这样的交易对你没有利.
2.上述问题中,你发现了什么问题
提示:函数y=ax(a>1)与y=kx(k>0)都是增函数,随着x的增大,指数函数的增长速度越
来越快,相比指数函数,一次函数增长得较慢.
常见的函数模型及增长特点
1.线性函数模型y=kx+b(k>0)的增长特点是增长速度不变,可称为“直线上升”.
2.指数函数模型y=ax(a>1)的增长特点是随着自变量的增大,函数值增大的速度越
来越快,即增长速度急剧,形象地称为“指数爆炸”.
3.对数函数模型y=logax(a>1)的增长特点是随着自变量的增大,函数值增大的速度
越来越慢,即增长速度平缓,可称为“对数增长”.
甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程fi(x)
(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为f1(x)=2x-1, f2(x)=x2, f3(x)=x, f4(x)=
log2(x+1),有以下结论:
①当x>1时,甲在最前面;
②当x>1时,乙在最前面;
③当0
④丙不可能在最前面,也不可能在最后面;
⑤如果它们一直运动下去,那么最终在最前面的是甲.
其中,所有正确结论的序号为 ③④⑤ .
解析 路程fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为f1(x)=2x-1, f2(x)=x2,
f3(x)=x, f4(x)=log2(x+1),它们相对应的函数模型分别是指数型函数、二次函数、
一次函数和对数型函数.
当x=2时, f1(2)=3, f2(2)=4,∴①不正确;
当x=5时, f1(5)=31, f2(5)=25,∴②不正确;
根据四种函数的变化特点,画出四个函数的图象,
可知当x=1时,甲、乙、丙、丁四个物体的路程相等,而对数型函数的增长速度是
先快后慢,从而当0
结合各函数图象的变化情况,可知丙不可能在最前面,也不可能在最后面,∴④正
确;
指数函数的增长速度急剧,故若运动的时间足够长,则最前面的物体一定是按照
指数型函数运动的物体,即一定是甲,∴⑤正确.
2 | 几种常见的函数模型的选择
不同的函数模型能刻画现实世界中不同的变化规律:
(1)线性函数模型适合描述增长速度不变的变化规律;
(2)指数函数模型适合描述增长速度急剧的变化规律;
(3)对数函数、幂函数模型适合描述增长速度平缓的变化规律.
因此,需抓住题中蕴含的数学信息,恰当、准确地建立相应变化规律的函数模型
来解决实际问题.
某皮鞋厂今年1月份开始投产,并且前4个月的产量分别为1万双,1.2万双,1.3
万双,1.37万双.由于产品质量好、款式新颖,前几个月的销售情况良好.为了推销
员在推销产品时接受订单不至于过多或过少,需要估计以后几个月的产量,且厂
里暂时不准备增加设备和工人.假如你是厂长,就月份为x,产量为y给出三种函数
模型:y=ax+b,y=ax2+bx+c,y=abx+c,其中a≠0,你将利用哪一种模型去估算以后几个
月的产量
解析 由题意知,将产量随时间变化的数据分别表示为A(1,1),B(2,1.2),C(3,1.3),
D(4,1.37).
(1)若选择函数y=ax+b,
将B,C两点的坐标代入函数解析式,
得 解得
∴y=0.1x+1.
由此可得结论:在不增加工人和设备的条件下,产量会每月增加1 000双,这是不太
可能的.
(2)若选择函数y=ax2+bx+c,将A,B,C三点的坐标代入函数解析式,
得
解得
∴y=-0.05x2+0.35x+0.7.
由此式计算得4月份的产量为1.3万双,比实际产量少700双,而且由二次函数的性
质可知,产量自4月份开始每月下降,不符合实际.
(3)若选择函数y=abx+c,
将A,B,C三点的坐标代入函数解析式,
得
由①得ab=1-c,代入②③,
得 解得
则a= =-0.8,
∴y=-0.8×0.5x+1.4.
把x=4代入,得y=-0.8×0.54+1.4=1.35.故在三个函数模型中y=abx+c的误差最小.
随着工人技术和管理效益逐渐提高,一段时间内产量会明显上升,但经过一段时
间之后,如果不增加设备和工人,产量必然趋于稳定,而y=-0.8×0.5x+1.4恰好反映了
这种趋势.
因此选用函数模型y=-0.8×0.5x+1.4比较接近客观实际.
题组一 不同函数增长的差异
1.下列函数中,增长速度越来越慢的是 ( B )
A.y=6x B.y=log6x C.y=x6 D.y=6x
2.某校甲、乙两食堂某年1月份的营业额相等,甲食堂的营业额逐月增加,并且每月的增加值相同;乙食堂的营业额也逐月增加,且每月增加的百分率相同.已知同年9月份两食堂的营业额又相等,则同年5月份 ( A )
A.甲食堂的营业额较高 B.乙食堂的营业额较高
C.甲、乙两食堂的营业额相同 D.不能确定甲、乙哪个食堂的营业额较高
3.(2020湖南醴陵一中高一上期中)已知函数y1=2x,y2=x2,y3=log2x,在区间(0,+∞)上一定存在x0,当x>x0时( A )
A.2x>x2>log2x B.x2>2x>log2x C.log2x>2x>x2 D.log2x>x2>2x
4.某小型贸易公司为了实现年终10万元利润的目标,特制订了一个销售人员年终绩效奖励方案:当销售利润为x万元(4≤x≤10)时,奖金y(万元)随销售利润x(万元)的增加而增加,但奖金总数不超过2万元,同时不超过销售利润的,则下列函数中,符合该公司奖励方案的函数模型是(参考数据:lg 2≈0.3,lg 3≈0.48,lg 5≈0.7) ( B )
A.y=0.4x B.y=lg x+1 C.y= D.y=1.125x
题组二 图象信息迁移问题
5.向高为H的水瓶内注水,一直到注满为止,如果注水量V与水深h的函数图象如图所示,那么水瓶的形状大致是 ( B )
6.(2021山东德州、烟台高一上期中联考)某高三学生于2020年9月第二个周末乘高铁赴济南参加全国高中数学联赛(山东省赛区)的比赛活动.早上他乘坐出租车从家里出发,离开家不久,发现身份证忘在家里了,于是回到家取上身份证,然后乘坐出租车以更快的速度赶往高铁站,令x(单位:分钟)表示他离开家的时间,y(单位:千米)表示离开家的距离,其中等待红绿灯及在家取身份证的时间忽略不计,出租车匀速行驶,则下列图象中与上述事件吻合最好的是 ( C )
7.(多选)如图所示的是某受污染的湖泊在自然净化的过程中某种有害物质的剩余量y与净化时间t(月)之间满足的函数关系:y=at(t≥0,a>0,a≠1)的图象.若有害物质的初始量为1,则以下说法中正确的是 ( ACD) )
A.第4个月时,剩余量就会低于
B.每月减少的有害物质的量都相等
C.有害物质每月的衰减率为
D.当剩余量为,, 时,所经过的时间分别是t1,t2,t3,则t1+t2=t3
C
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
