1.4.2 用空间向量研究距离、夹角问题课件-2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(47张PPT)
文档属性
| 名称 | 1.4.2 用空间向量研究距离、夹角问题课件-2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(47张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 21:43:54 | ||
图片预览





文档简介
(共47张PPT)
1.4.2 用空间向量研究距离、夹角问题
——距离问题
空间的距离问题有:线线距、线面距、面面距
我们知道,立体几何中的距离问题包括点到直线、点到平面、两条平行直线以及两个平行平面的距离问题等,如何用空间向量解决这些距离问题呢
下面我们先研究用向量方法求直线l外一点P到直线l的距离.
探究 已知直线l的单位方向向量为 , A是直线l上的定点,P是直线l外一点. 如何利用这些条件求点P到直线l的距离
A
l
P
Q
如图示,向量 在直线l上的投影向量为 ,则△APQ是直角三角形,因为A,P都是定点,所以 与 的夹角∠PAQ都是确定的. 于 是可求 再利用勾股定理,可以求出点P到直线l的距离PQ.
设 ,则向量 在直线l上的投影向量
在Rt△APQ中,由勾股定理,得
若直线l的法向量为 ,则点P到直线l的距离为
d
1. 点到直线的距离:
3. 向量法.
立体几何中点到平面距离的求法:
1. 直接法;
2. 等体积法;
下面我们探究用空间向量求平面α外一点P到平面α的距离.
如图示,已知平面α的法向量为 ,A是平面α内的定点,P是平面α外一点. 过点P作平面α的垂线l,交平面α于点Q,则 是直线l的方向向量,且点P到平面α的距离d就是AP在直线l上的投影向量 的长度. 因此
α
A
l
Q
P
d
思考 类比点到直线的距离的求法,如何求两条平行直线之间的距离
2. 两平行直线间的距离:
两条平行直线之间的距离可转化为点到直线距离求解.
m
n
A
d
3. 点到平面的距离:
4. 直线到平面的距离:
直线到平面的距离可转化为点到平面的距离求解.
3. 两个平行平面之间的距离:
α
A
l
Q
d
P
两个平行平面之间的距离也可转化为点到平面的距离求解.
α
A
Q
d
P
β
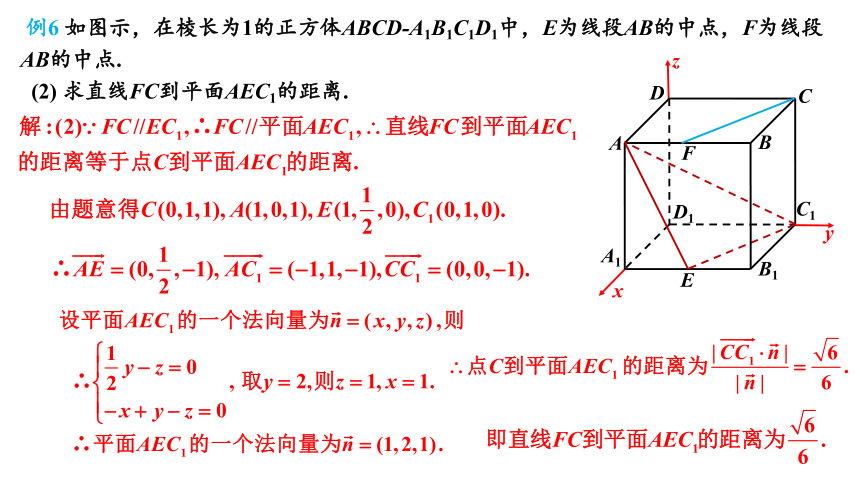
例6 如图示,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段AB的中点,F为线段AB的中点.
(1) 求点B到直线AC1的距离;
(2) 求直线FC到平面AEC1的距离.
x
y
z
B
A
A1
B1
C1
D1
C
D
E
F
例6 如图示,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段AB的中点,F为线段AB的中点.
(2) 求直线FC到平面AEC1的距离.
x
y
z
B
A
A1
B1
C1
D1
C
D
E
F
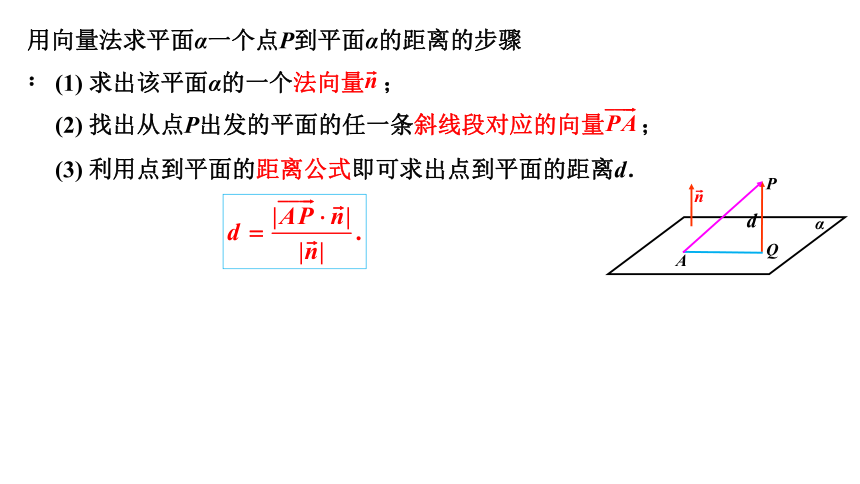
用向量法求平面α一个点P到平面α的距离的步骤:
(3) 利用点到平面的距离公式即可求出点到平面的距离d.
(1) 求出该平面α的一个法向量 ;
α
A
Q
P
d
(2) 找出从点P出发的平面的任一条斜线段对应的向量 ;
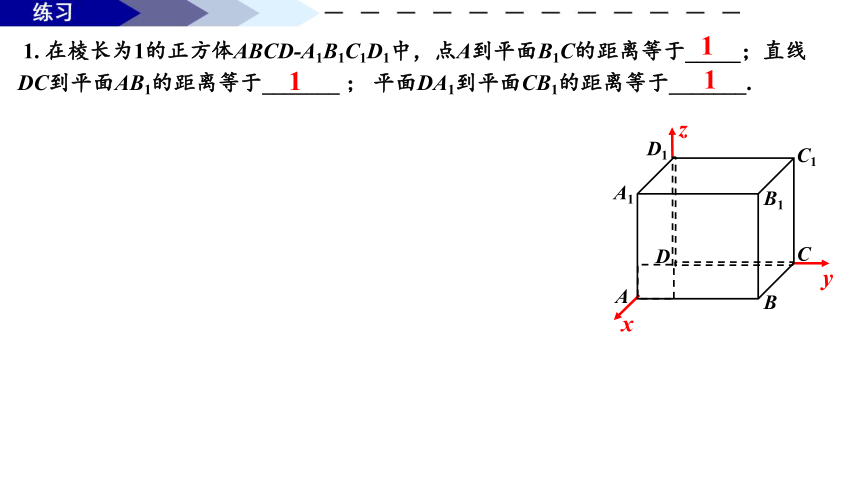
1. 在棱长为1的正方体ABCD-A1B1C1D1中,点A到平面B1C的距离等于_____;直线DC到平面AB1的距离等于_______ ; 平面DA1到平面CB1的距离等于_______.
x
y
z
A1
D1
B1
D
B
C
C1
A
1
1
1
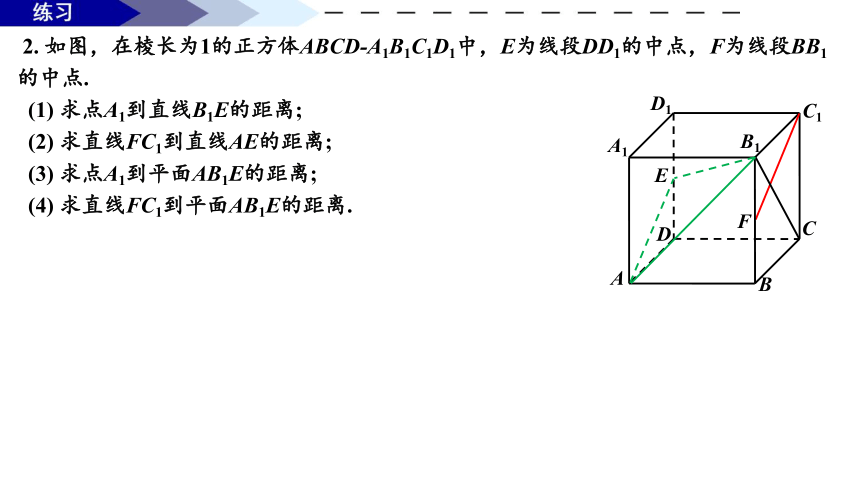
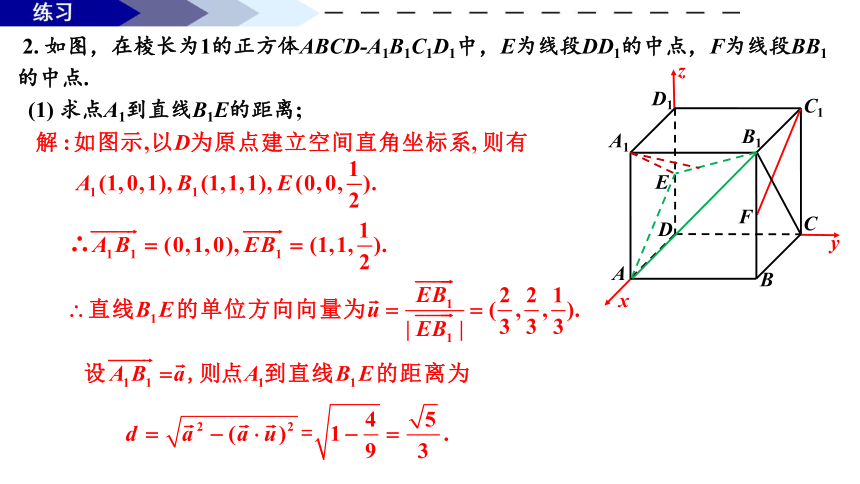
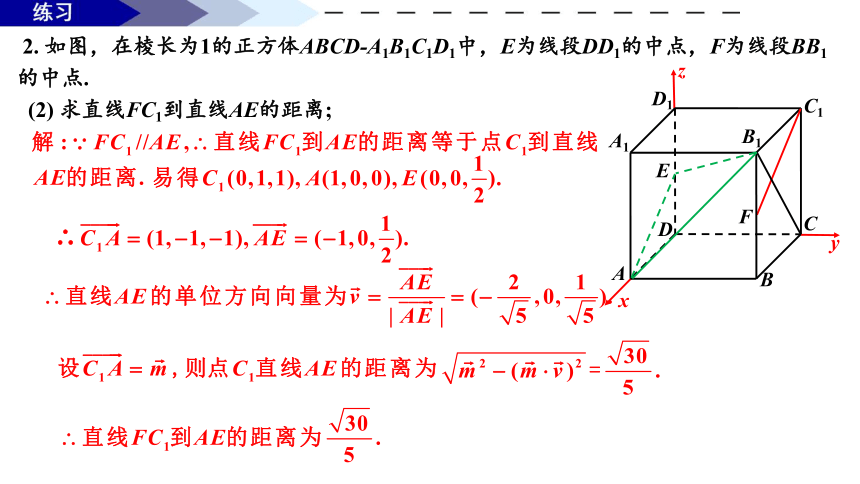
2. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点.
(1) 求点A1到直线B1E的距离;
(2) 求直线FC1到直线AE的距离;
(3) 求点A1到平面AB1E的距离;
(4) 求直线FC1到平面AB1E的距离.
B
A
A1
B1
C1
D1
C
D
E
F
2. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点.
(1) 求点A1到直线B1E的距离;
x
y
z
B
A
A1
B1
C1
D1
C
D
E
F
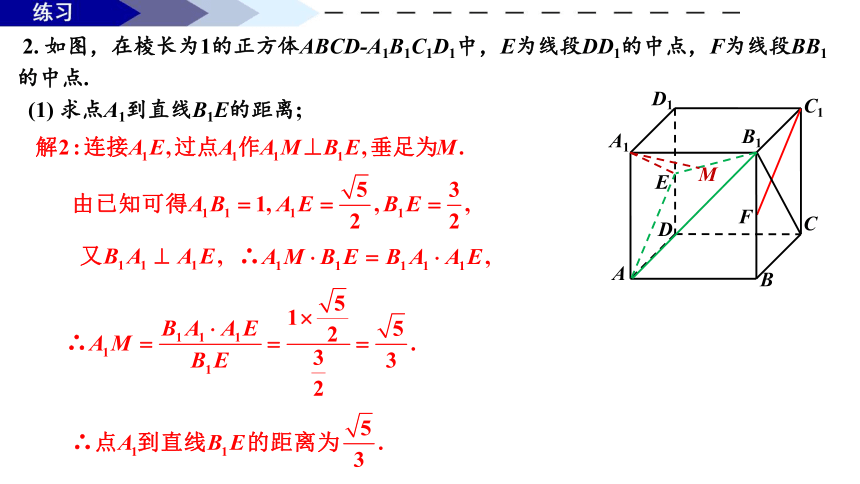
2. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点.
(1) 求点A1到直线B1E的距离;
B
A
A1
B1
C1
D1
C
D
E
F
M
2. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点.
(2) 求直线FC1到直线AE的距离;
x
y
z
B
A
A1
B1
C1
D1
C
D
E
F
2. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点.
(3) 求点A1到平面AB1E的距离;
x
y
z
B
A
A1
B1
C1
D1
C
D
E
F
2. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点.
(4) 求直线FC1到平面AB1E的距离.
x
y
z
B
A
A1
B1
C1
D1
C
D
E
F
3. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,求平面A1DB与平面D1CB1的距离.
x
y
z
B
A
A1
B1
C1
D1
C
D
x
y
z
【巩固训练1】已知正方形ABCD的边长为4,CG⊥平面ABCD,CG=2,E, F分别是AB, AD的中点,求点B到平面GEF的距离.
D
A
B
C
G
F
E
解:如图,建立空间直角坐标系Cxyz.由题设得
B(0,4,0), E(2,4,0), F(4,2,0), G(0,0,2).则
设平面EFG的一个法向量为
设点B到平面GEF的距离为d,则
∴点B到平面GEF的距离为
取x=1, 则y=1, z=3.
【巩固训练2】已知正方形ABCD的边长为4,CG⊥平面ABCD,CG=2,E, F分别是AB, AD的中点,求点BD到平面GEF的距离.
x
y
z
D
A
B
C
G
F
E
x
y
z
【巩固训练3】如图,正方体ABCD和ABEF的边长都是1,且它们所在平面互相垂直,点M在AC上,点N在BF上,若CM = BN = ,求MN的长.
解1:建立如图所示的空间直角坐标系. 则有
【巩固训练3】如图,正方体ABCD和ABEF的边长都是1,且它们所在平面互相垂直,点M在AC上,点N在BF上,若CM = BN = ,求MN的长.
解2:
【巩固训练4】如图,两条异面直线a, b所成的角为θ,在直线a, b上分别取点A′, E和点A, F,使AA′⊥a,且AA′⊥b (AA′称为异面直线a, b的公垂线). 已知A′E=m, AF=n,EF=l,求公垂线AA′的长.
A′
A
b
a
F
E
1.4.2 用空间向量研究距离、夹角问题
——夹角问题
空间的角常见的有:线线角、线面角、面面角
1. 线线角 (异面直线所成的角)
距离类似,角度是立体几何中另一个重要的度量. 下 面我们用向量方法研究直线与直线所成的角、直线与平面所成的角以及平面与平面的夹角,先看线线角.
一般地,两条异面直线所成的角,可以转化为两条异面直线的方向向量的夹角来求得. 也就是说,若异面直线l1, l2所成的角为θ,其方向向量分别是 则
l1
l2
l1
l2
例7 如图示,在棱长为1的正四面体(四个面都是正三角形) ABCD中,M, N分别为BC, AD的中点,求直线AM和CN夹角的余弦值.
A
C
D
B
M
N
1. 在直三棱柱ABC-A1B1C1中,∠BCA=90°,D1, F1分别是A1B1, A1C1的中点,BC=CA =CC1. 则BD1与AF1所成角的余弦值是( ).
A
C
B
A1
C1
B1
F1
D1
x
y
z
A
1. 在直三棱柱ABC-A1B1C1中,∠BCA=90°,D1, F1分别是A1B1, A1C1的中点,BC=CA =CC1. 则BD1与AF1所成角的余弦值是( ).
A
C
B
A1
C1
B1
F1
D1
A
2. 线面角 (直线与平面所成的角)
类似地,直线与平面所成的角,可以转化为直线的方向向量与平面的法向量的夹角.如图示,直线AB与平面α相交于点B,设直线AB与平面α所成的角为θ,直线AB的方向向量 ,平面α的法向量为 ,则
α
A
B
C
【例题】在长方体ABCD-A1B1C1D1中, AB=6, AD=8, AA1=6,M是B1C1上的一 点,且B1M=2,点N在线段A1D上, A1N=5, 求AD与平面ANM所成角的正弦值.
z
y
x
A
B
C
A1
B1
C1
D1
D
N
M
3.如图,在三棱锥O-ABC中,OA, OB, OC两两垂直,OA=OC=3,OB=2. 求直线OB与平面ABC所成角的正弦值. (P41练习3)
B
O
C
A
x
y
z
2. PA, PB, PC是从点P出发的三条射线,每两条射线的夹角均为60°,那么直线PC与平面PAB所成角的余弦值是( ). (P38练习2)
P
B
C
A
D
O
F
E
解: 过PC上任取一点D并作PO⊥平面APB ,则∠DPO就是直线PC与平面PAB所成的角.
过点O作OE⊥PA, OF⊥PB, ∵ DO⊥平面APB, 则DE⊥PA, DF⊥PB. ∴△DEP≌△DFP, ∴EP=FP,∴△OEP≌△OFP.
∴点O在∠APB的平分线上, 即∠OPE=30° .
2. PA, PB, PC是从点P出发的三条射线,每两条射线的夹角均为60°,那么直线PC与平面PAB所成角的余弦值是( ). (P38练习2)
解2:如图示, 建立空间直角坐标系, 设正方体棱长为1, 则
P
C
B
A
x
y
z
O
3. 面面角 (平面与平面的夹角)
如图示,平面α与平面β相交,形成四个二面角,我们把这四个二面角中不大于90°的二面角称为平面α与平面β的夹角.
类似于两条异面直线所成的角,若平面α, β的法向量分别是 和 ,则平面α与平面β的夹角即为向量 和 的夹角或其补角,设平面α与平面β的夹角为θ,则
思考 右图中有几个二面角 两个平面的夹角与这两个平面形成的二面角有什么关系
相等或互补
设二面角α-l-β的平面角为θ0,则有
例8 如图 示,在直三棱柱ABC-A1B1C1中,AC=CB=2,AA1=3,∠ACB=90°,P为BC的中点,点Q, R分别在棱AA1,BB1上,A1Q= 2AQ,BR= 2RB1. 求平面PQR与平面A1B1C1夹角的余弦值.
A
C
B
A1
C1
B1
Q
P
R
x
y
z
3.如图,正三棱柱ABC-A1B1C1的所有棱长都为2,求平面AA1B与平面A1BC1夹角的余弦值. (P38练习3)
A
C
B
A1
C1
B1
x
y
z
O
4. 如图,△ABC和△DBC所在平面垂直,且AB= BC=BD,∠CBA=∠DBC=120°. 求:
(1) 直线AD与直线BC所成角的大小;
D
B
C
A
x
y
z
O
4. 如图,△ABC和△DBC所在平面垂直,且AB= BC=BD,∠CBA=∠DBC=120°. 求:
(2) 直线AD与平面BCD所成角的大小;
D
B
C
A
x
y
z
O
4. 如图,△ABC和△DBC所在平面垂直,且AB= BC=BD,∠CBA=∠DBC=120°. 求:
(3) 平面ABD和平面BDC的夹角的余弦值.
D
B
C
A
x
y
z
O
例9 某种礼物降落伞的示意图如图示,其中有8根绳子和伞面连接,每根绳子和水平面的法向量的夹角均为30°. 已知礼物的质量为1kg,每根绳子的拉力大小相同. 求降落伞在匀速下落的过程中每根绳子拉力的大小(重力加速度g取9.8 m/s2,精确到0. 01 N).
如图示,设水平面的单位法向量为 ,其中每一根绳子的拉力均为 . 因为 =30°,所以 在 上的投影向量为 .
所以8根绳子拉力的合力为
又因为降落伞匀速下落,所以
∴ 每根绳子拉力的大小为1.41 N.
解:
例10 如图示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1) 求证: PA//平面EDB;
(2) 求证: PB⊥平面EFD;
(3) 求平面CPB与平面PBD的夹角的大小.
B
C
D
A
P
E
F
x
y
z
(1) 证明: 连接AC, 交BD于点G, 连接EG. 依题意得
如图,以D为原点建立空间直角坐标系Dxyz,设DC= 2.
解:
G
因为底面ABCD是正方形, 所以点G是它的中心,
故点G的坐标为(1,1,0), 且
A(2,0,0), P(0,0,2), E(0,1,1).
即PA//EG.
而EG 平面EDB,且PA 平面EDB, 因此PA//平面EDB.
例10 如图示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1) 求证: PA//平面EDB;
(2) 求证: PB⊥平面EFD;
(3) 求平面CPB与平面PBD的夹角的大小.
B
C
D
A
P
E
F
x
y
z
依题意得 B(2,2,0).
G
∴PB⊥DE.
由已知EF⊥PB,且EF∩DE=E,
∴PB⊥平面EFD.
(2) 证明:
例10 如图示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1) 求证: PA//平面EDB;
(2) 求证: PB⊥平面EFD;
(3) 求平面CPB与平面PBD的夹角的大小.
B
C
D
A
P
E
F
x
y
z
已知PB⊥EF,由(2)可知PB⊥DF,故∠EFD是平面CPB与平面PBD的夹角. 设F(x,y,z), 则
G
∴ ∠EFD=60°.
(3) 解1:
∴平面CPB与平面PBD的夹角的大小为60°.
(3) 解2:
例10 如图示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(3) 求平面CPB与平面PBD的夹角的大小.
B
C
D
A
P
E
F
x
y
z
G
1. 如图, 二面角α-l-β的棱上有两个点A, B, 线段BD与AC分别在这个二面角的两个面内, 并且都垂直于棱l. 若AB=4, AC=6, BD=8, CD= , 求平面α与平面β的夹角.
α
l
β
A
B
C
D
1. 如图, 二面角α-l-β的棱上有两个点A, B, 线段BD与AC分别在这个二面角的两个面内, 并且都垂直于棱l. 若AB=4, AC=6, BD=8, CD= , 求平面α与平面β的夹角.
α
l
β
A
B
C
D
E
2. 如图,在三棱锥A-BCD中,AB=AC=BD=CD=3,AD=BC=2,M, N分别是AD,BC的中点,求异面直线AN, CM所成角的余弦值.
A
C
D
B
N
M
E
x
y
z
A
B
C
A1
B1
C1
D1
D
F
E
K
G
H
L
x
y
z
A
B
C
A1
B1
C1
D1
D
F
E
K
G
H
L
x
y
z
A
B
C
A1
B1
C1
D1
D
F
E
K
G
H
L
1.4.2 用空间向量研究距离、夹角问题
——距离问题
空间的距离问题有:线线距、线面距、面面距
我们知道,立体几何中的距离问题包括点到直线、点到平面、两条平行直线以及两个平行平面的距离问题等,如何用空间向量解决这些距离问题呢
下面我们先研究用向量方法求直线l外一点P到直线l的距离.
探究 已知直线l的单位方向向量为 , A是直线l上的定点,P是直线l外一点. 如何利用这些条件求点P到直线l的距离
A
l
P
Q
如图示,向量 在直线l上的投影向量为 ,则△APQ是直角三角形,因为A,P都是定点,所以 与 的夹角∠PAQ都是确定的. 于 是可求 再利用勾股定理,可以求出点P到直线l的距离PQ.
设 ,则向量 在直线l上的投影向量
在Rt△APQ中,由勾股定理,得
若直线l的法向量为 ,则点P到直线l的距离为
d
1. 点到直线的距离:
3. 向量法.
立体几何中点到平面距离的求法:
1. 直接法;
2. 等体积法;
下面我们探究用空间向量求平面α外一点P到平面α的距离.
如图示,已知平面α的法向量为 ,A是平面α内的定点,P是平面α外一点. 过点P作平面α的垂线l,交平面α于点Q,则 是直线l的方向向量,且点P到平面α的距离d就是AP在直线l上的投影向量 的长度. 因此
α
A
l
Q
P
d
思考 类比点到直线的距离的求法,如何求两条平行直线之间的距离
2. 两平行直线间的距离:
两条平行直线之间的距离可转化为点到直线距离求解.
m
n
A
d
3. 点到平面的距离:
4. 直线到平面的距离:
直线到平面的距离可转化为点到平面的距离求解.
3. 两个平行平面之间的距离:
α
A
l
Q
d
P
两个平行平面之间的距离也可转化为点到平面的距离求解.
α
A
Q
d
P
β
例6 如图示,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段AB的中点,F为线段AB的中点.
(1) 求点B到直线AC1的距离;
(2) 求直线FC到平面AEC1的距离.
x
y
z
B
A
A1
B1
C1
D1
C
D
E
F
例6 如图示,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段AB的中点,F为线段AB的中点.
(2) 求直线FC到平面AEC1的距离.
x
y
z
B
A
A1
B1
C1
D1
C
D
E
F
用向量法求平面α一个点P到平面α的距离的步骤:
(3) 利用点到平面的距离公式即可求出点到平面的距离d.
(1) 求出该平面α的一个法向量 ;
α
A
Q
P
d
(2) 找出从点P出发的平面的任一条斜线段对应的向量 ;
1. 在棱长为1的正方体ABCD-A1B1C1D1中,点A到平面B1C的距离等于_____;直线DC到平面AB1的距离等于_______ ; 平面DA1到平面CB1的距离等于_______.
x
y
z
A1
D1
B1
D
B
C
C1
A
1
1
1
2. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点.
(1) 求点A1到直线B1E的距离;
(2) 求直线FC1到直线AE的距离;
(3) 求点A1到平面AB1E的距离;
(4) 求直线FC1到平面AB1E的距离.
B
A
A1
B1
C1
D1
C
D
E
F
2. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点.
(1) 求点A1到直线B1E的距离;
x
y
z
B
A
A1
B1
C1
D1
C
D
E
F
2. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点.
(1) 求点A1到直线B1E的距离;
B
A
A1
B1
C1
D1
C
D
E
F
M
2. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点.
(2) 求直线FC1到直线AE的距离;
x
y
z
B
A
A1
B1
C1
D1
C
D
E
F
2. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点.
(3) 求点A1到平面AB1E的距离;
x
y
z
B
A
A1
B1
C1
D1
C
D
E
F
2. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点.
(4) 求直线FC1到平面AB1E的距离.
x
y
z
B
A
A1
B1
C1
D1
C
D
E
F
3. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,求平面A1DB与平面D1CB1的距离.
x
y
z
B
A
A1
B1
C1
D1
C
D
x
y
z
【巩固训练1】已知正方形ABCD的边长为4,CG⊥平面ABCD,CG=2,E, F分别是AB, AD的中点,求点B到平面GEF的距离.
D
A
B
C
G
F
E
解:如图,建立空间直角坐标系Cxyz.由题设得
B(0,4,0), E(2,4,0), F(4,2,0), G(0,0,2).则
设平面EFG的一个法向量为
设点B到平面GEF的距离为d,则
∴点B到平面GEF的距离为
取x=1, 则y=1, z=3.
【巩固训练2】已知正方形ABCD的边长为4,CG⊥平面ABCD,CG=2,E, F分别是AB, AD的中点,求点BD到平面GEF的距离.
x
y
z
D
A
B
C
G
F
E
x
y
z
【巩固训练3】如图,正方体ABCD和ABEF的边长都是1,且它们所在平面互相垂直,点M在AC上,点N在BF上,若CM = BN = ,求MN的长.
解1:建立如图所示的空间直角坐标系. 则有
【巩固训练3】如图,正方体ABCD和ABEF的边长都是1,且它们所在平面互相垂直,点M在AC上,点N在BF上,若CM = BN = ,求MN的长.
解2:
【巩固训练4】如图,两条异面直线a, b所成的角为θ,在直线a, b上分别取点A′, E和点A, F,使AA′⊥a,且AA′⊥b (AA′称为异面直线a, b的公垂线). 已知A′E=m, AF=n,EF=l,求公垂线AA′的长.
A′
A
b
a
F
E
1.4.2 用空间向量研究距离、夹角问题
——夹角问题
空间的角常见的有:线线角、线面角、面面角
1. 线线角 (异面直线所成的角)
距离类似,角度是立体几何中另一个重要的度量. 下 面我们用向量方法研究直线与直线所成的角、直线与平面所成的角以及平面与平面的夹角,先看线线角.
一般地,两条异面直线所成的角,可以转化为两条异面直线的方向向量的夹角来求得. 也就是说,若异面直线l1, l2所成的角为θ,其方向向量分别是 则
l1
l2
l1
l2
例7 如图示,在棱长为1的正四面体(四个面都是正三角形) ABCD中,M, N分别为BC, AD的中点,求直线AM和CN夹角的余弦值.
A
C
D
B
M
N
1. 在直三棱柱ABC-A1B1C1中,∠BCA=90°,D1, F1分别是A1B1, A1C1的中点,BC=CA =CC1. 则BD1与AF1所成角的余弦值是( ).
A
C
B
A1
C1
B1
F1
D1
x
y
z
A
1. 在直三棱柱ABC-A1B1C1中,∠BCA=90°,D1, F1分别是A1B1, A1C1的中点,BC=CA =CC1. 则BD1与AF1所成角的余弦值是( ).
A
C
B
A1
C1
B1
F1
D1
A
2. 线面角 (直线与平面所成的角)
类似地,直线与平面所成的角,可以转化为直线的方向向量与平面的法向量的夹角.如图示,直线AB与平面α相交于点B,设直线AB与平面α所成的角为θ,直线AB的方向向量 ,平面α的法向量为 ,则
α
A
B
C
【例题】在长方体ABCD-A1B1C1D1中, AB=6, AD=8, AA1=6,M是B1C1上的一 点,且B1M=2,点N在线段A1D上, A1N=5, 求AD与平面ANM所成角的正弦值.
z
y
x
A
B
C
A1
B1
C1
D1
D
N
M
3.如图,在三棱锥O-ABC中,OA, OB, OC两两垂直,OA=OC=3,OB=2. 求直线OB与平面ABC所成角的正弦值. (P41练习3)
B
O
C
A
x
y
z
2. PA, PB, PC是从点P出发的三条射线,每两条射线的夹角均为60°,那么直线PC与平面PAB所成角的余弦值是( ). (P38练习2)
P
B
C
A
D
O
F
E
解: 过PC上任取一点D并作PO⊥平面APB ,则∠DPO就是直线PC与平面PAB所成的角.
过点O作OE⊥PA, OF⊥PB, ∵ DO⊥平面APB, 则DE⊥PA, DF⊥PB. ∴△DEP≌△DFP, ∴EP=FP,∴△OEP≌△OFP.
∴点O在∠APB的平分线上, 即∠OPE=30° .
2. PA, PB, PC是从点P出发的三条射线,每两条射线的夹角均为60°,那么直线PC与平面PAB所成角的余弦值是( ). (P38练习2)
解2:如图示, 建立空间直角坐标系, 设正方体棱长为1, 则
P
C
B
A
x
y
z
O
3. 面面角 (平面与平面的夹角)
如图示,平面α与平面β相交,形成四个二面角,我们把这四个二面角中不大于90°的二面角称为平面α与平面β的夹角.
类似于两条异面直线所成的角,若平面α, β的法向量分别是 和 ,则平面α与平面β的夹角即为向量 和 的夹角或其补角,设平面α与平面β的夹角为θ,则
思考 右图中有几个二面角 两个平面的夹角与这两个平面形成的二面角有什么关系
相等或互补
设二面角α-l-β的平面角为θ0,则有
例8 如图 示,在直三棱柱ABC-A1B1C1中,AC=CB=2,AA1=3,∠ACB=90°,P为BC的中点,点Q, R分别在棱AA1,BB1上,A1Q= 2AQ,BR= 2RB1. 求平面PQR与平面A1B1C1夹角的余弦值.
A
C
B
A1
C1
B1
Q
P
R
x
y
z
3.如图,正三棱柱ABC-A1B1C1的所有棱长都为2,求平面AA1B与平面A1BC1夹角的余弦值. (P38练习3)
A
C
B
A1
C1
B1
x
y
z
O
4. 如图,△ABC和△DBC所在平面垂直,且AB= BC=BD,∠CBA=∠DBC=120°. 求:
(1) 直线AD与直线BC所成角的大小;
D
B
C
A
x
y
z
O
4. 如图,△ABC和△DBC所在平面垂直,且AB= BC=BD,∠CBA=∠DBC=120°. 求:
(2) 直线AD与平面BCD所成角的大小;
D
B
C
A
x
y
z
O
4. 如图,△ABC和△DBC所在平面垂直,且AB= BC=BD,∠CBA=∠DBC=120°. 求:
(3) 平面ABD和平面BDC的夹角的余弦值.
D
B
C
A
x
y
z
O
例9 某种礼物降落伞的示意图如图示,其中有8根绳子和伞面连接,每根绳子和水平面的法向量的夹角均为30°. 已知礼物的质量为1kg,每根绳子的拉力大小相同. 求降落伞在匀速下落的过程中每根绳子拉力的大小(重力加速度g取9.8 m/s2,精确到0. 01 N).
如图示,设水平面的单位法向量为 ,其中每一根绳子的拉力均为 . 因为 =30°,所以 在 上的投影向量为 .
所以8根绳子拉力的合力为
又因为降落伞匀速下落,所以
∴ 每根绳子拉力的大小为1.41 N.
解:
例10 如图示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1) 求证: PA//平面EDB;
(2) 求证: PB⊥平面EFD;
(3) 求平面CPB与平面PBD的夹角的大小.
B
C
D
A
P
E
F
x
y
z
(1) 证明: 连接AC, 交BD于点G, 连接EG. 依题意得
如图,以D为原点建立空间直角坐标系Dxyz,设DC= 2.
解:
G
因为底面ABCD是正方形, 所以点G是它的中心,
故点G的坐标为(1,1,0), 且
A(2,0,0), P(0,0,2), E(0,1,1).
即PA//EG.
而EG 平面EDB,且PA 平面EDB, 因此PA//平面EDB.
例10 如图示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1) 求证: PA//平面EDB;
(2) 求证: PB⊥平面EFD;
(3) 求平面CPB与平面PBD的夹角的大小.
B
C
D
A
P
E
F
x
y
z
依题意得 B(2,2,0).
G
∴PB⊥DE.
由已知EF⊥PB,且EF∩DE=E,
∴PB⊥平面EFD.
(2) 证明:
例10 如图示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1) 求证: PA//平面EDB;
(2) 求证: PB⊥平面EFD;
(3) 求平面CPB与平面PBD的夹角的大小.
B
C
D
A
P
E
F
x
y
z
已知PB⊥EF,由(2)可知PB⊥DF,故∠EFD是平面CPB与平面PBD的夹角. 设F(x,y,z), 则
G
∴ ∠EFD=60°.
(3) 解1:
∴平面CPB与平面PBD的夹角的大小为60°.
(3) 解2:
例10 如图示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(3) 求平面CPB与平面PBD的夹角的大小.
B
C
D
A
P
E
F
x
y
z
G
1. 如图, 二面角α-l-β的棱上有两个点A, B, 线段BD与AC分别在这个二面角的两个面内, 并且都垂直于棱l. 若AB=4, AC=6, BD=8, CD= , 求平面α与平面β的夹角.
α
l
β
A
B
C
D
1. 如图, 二面角α-l-β的棱上有两个点A, B, 线段BD与AC分别在这个二面角的两个面内, 并且都垂直于棱l. 若AB=4, AC=6, BD=8, CD= , 求平面α与平面β的夹角.
α
l
β
A
B
C
D
E
2. 如图,在三棱锥A-BCD中,AB=AC=BD=CD=3,AD=BC=2,M, N分别是AD,BC的中点,求异面直线AN, CM所成角的余弦值.
A
C
D
B
N
M
E
x
y
z
A
B
C
A1
B1
C1
D1
D
F
E
K
G
H
L
x
y
z
A
B
C
A1
B1
C1
D1
D
F
E
K
G
H
L
x
y
z
A
B
C
A1
B1
C1
D1
D
F
E
K
G
H
L
