4.5 牛顿运动定律的应用 学案(word版含答案)
文档属性
| 名称 | 4.5 牛顿运动定律的应用 学案(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 333.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-11-23 00:00:00 | ||
图片预览


文档简介
《运动和力的关系》
“牛顿运动定律的应用”章节考点归纳&典例示范
1.从受力确定运动情况
如果已知物体的受力情况,可以由牛顿第二定律求出物体的加速度,再通过运动学的规律确定物体的运动情况。
(1)从受力确定运动情况的一般求解步骤
(2)解题方法
(1)合成法:物体只受两个力的作用产生加速度时,合力的方向就是加速度的方向,解题时要求准确作出力的平行四边形,然后运用几何知识求合力F合。反之,若知道加速度方向就知道合力方向。
(2)正交分解法:当物体受到两个以上的力作用而产生加速度时,通常用正交分解法解答,一般把力正交分解为沿加速度方向和垂直于加速度方向的两个分量。即沿加速度方向:Fx=ma,垂直于加速度方向:Fy=0。
2.从运动情况确定受力
如果已知物体的运动情况,根据运动学规律求出物体的加速度,结合受力分析,再根据牛顿第二定律求出力。
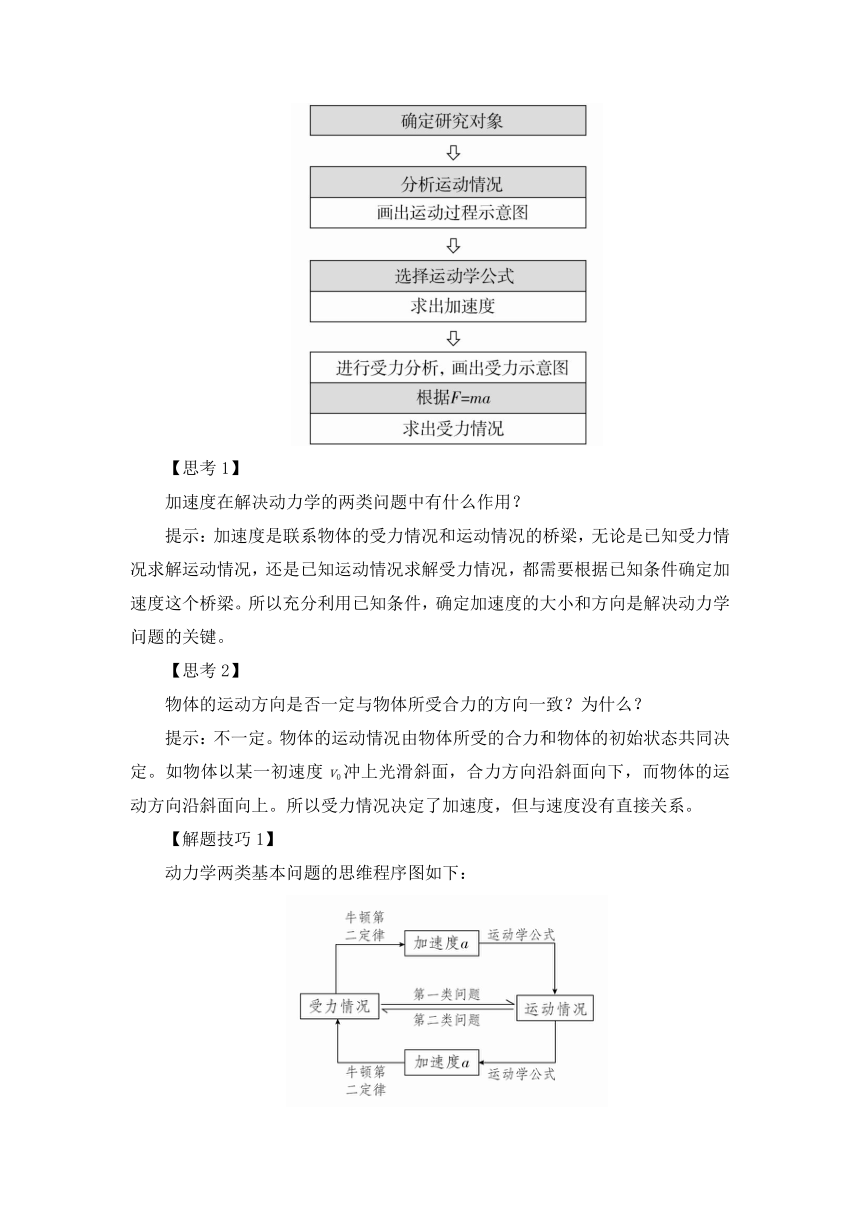
从运动情况确定受力的一般求解步骤
【思考1】
加速度在解决动力学的两类问题中有什么作用?
提示:加速度是联系物体的受力情况和运动情况的桥梁,无论是已知受力情况求解运动情况,还是已知运动情况求解受力情况,都需要根据已知条件确定加速度这个桥梁。所以充分利用已知条件,确定加速度的大小和方向是解决动力学问题的关键。
【思考2】
物体的运动方向是否一定与物体所受合力的方向一致?为什么?
提示:不一定。物体的运动情况由物体所受的合力和物体的初始状态共同决定。如物体以某一初速度v0冲上光滑斜面,合力方向沿斜面向下,而物体的运动方向沿斜面向上。所以受力情况决定了加速度,但与速度没有直接关系。
【解题技巧1】
动力学两类基本问题的思维程序图如下:
由图可见,不论求解哪一类问题,加速度都是解题的桥梁和纽带,求解出加速度是顺利解答的关键。
【解题技巧2】
多过程问题的分析:
物体的多过程运动问题是牛顿运动定律应用的较难题型,它展示了物体在运动过程中的受力特点及物体的运动情况,综合考查运用动力学相关知识处理实际运动问题的能力。
解答思路:首先理清物体的不同运动过程,根据受力特点确定各过程的运动性质,然后列相应的动力学方程(运用牛顿第二定律与运动学公式);注意不同过程中的中间衔接量,特别是两过程间的“速度”参量,往往是列式与计算的“桥梁”。
若运动过程涉及摩擦力,要分析好各阶段物体所受摩擦力的大小和方向,注意摩擦力是否发生突变。
【典例示范】
1.判断正误
(1)若已知物体的受力情况,可以由运动学公式求出加速度。( )
(2)若物体所受合外力恒定,且合外力方向与物体运动方向在同一条直线上,则根据牛顿第二定律求出物体做匀变速直线运动的加速度,再根据运动学公式求速度、位移等物理量。( )
(3)若物体做匀加速直线运动,则可以根据运动学公式求出加速度,进而根据牛顿运动定律求力。( )
(4)若已知物体的运动情况,可以根据牛顿第二定律求出加速度。( )
[答案](1)× (2)√ (3)√ (4)×
2.有一质量为1 kg的小球串在长0.5 m的轻杆顶部,轻杆与水平方向的夹角为θ=37°,静止释放小球,经过0.5 s小球到达轻杆底端,g取10 m/s2,试求:
(1)小球与轻杆之间的动摩擦因数;
(2)在竖直平面内给小球施加一个垂直于轻杆方向的恒力,使小球释放后加速度为2 m/s2,此恒力大小为多少?
答案 (1)0.25 (2)8 N或24 N
解析 (1)对小球,由牛顿第二定律得
mgsinθ-μmgcosθ=ma
又x=at2
联立解得μ=0.25。
(2)若F垂直于杆向下,则mgsinθ-μ(F+mgcosθ)=ma′
解得F=8 N;
若F垂直于杆向上,则mgsinθ-μ(F-mgcosθ)=ma′
解得F=24 N。
3.某游乐园的大型“跳楼机”游戏,以惊险刺激深受年轻人的欢迎。某次游戏中,质量为m=50 kg的小明同学坐在载人平台上,并系好安全带、锁好安全杆。游戏的过程简化为巨型升降机将平台拉升100 m高度,然后由静止开始下落,在忽略空气和台架对平台阻力的情况下,该运动可近似看作自由落体运动。在下落h1=80 m时启动制动系统使平台开始做匀减速运动,再下落h2=20 m时刚好停止运动。取g=10 m/s2,求:
(1)下落的过程中小明运动速度的最大值vm;
(2)落地前20 m内,小明做匀减速直线运动的加速度a的大小;
(3)当平台落到离地面10 m高的位置时,小明对平台的压力F的大小。
答案 (1)40 m/s (2)40 m/s2 (3)2500 N
解析 (1)当下落80 m时小明的速度最大,
v=2gh1
代入数据可得:vm=40 m/s。
(2)小明做匀减速运动过程中的加速度大小为
a2=
代入数据可得:a2=40 m/s2。
(3)当平台落到离地面10 m高的位置时,小明做匀减速运动,根据牛顿第二定律:F′-mg=ma2
代入数据得:F′=2500 N
根据牛顿第三定律,小明对平台的压力F为2500 N。
4.如图所示,质量为40 kg的雪橇(包括人)在与水平方向成37°角、大小为200 N的拉力F作用下,沿水平面由静止开始运动,经过2 s撤去拉力F,雪橇与地面间的动摩擦因数为0.20。取g=10 m/s2,cos37°=0.8,sin37°=0.6。求:
(1)刚撤去拉力时雪橇的速度v的大小;
(2)撤去拉力后雪橇能继续滑行的距离x。
答案 (1)5.2 m/s (2)6.76 m
解析 (1)对雪橇,竖直方向:N1+Fsin37°=mg
水平方向:Fcos37°-f1=ma1,且f1=μN1
由运动学公式:v=a1t1
解得:v=5.2 m/s。
(2)撤去拉力后,有-μmg=ma2,
则雪橇的加速度a2=-μg
根据0-v2=2a2x,解得:x=6.76 m。
5.如图所示,长为s=11.25 m的水平轨道AB与倾角为θ=37°、长为L=3 m的光滑斜面BC在B处连接,有一质量为m=2 kg的滑块(可视为质点),从A处由静止开始受到与水平方向成37°斜向上的拉力F=20 N的作用,经过一段时间后撤去拉力F,此时滑块仍在水平轨道上,但滑块恰好可以滑到斜面的最高点C。已知滑块经过B点时,速度方向改变但大小不变,滑块与AB间的动摩擦因数μ=0.5,重力加速度g取10 m/s2,sin37°=0.6,cos37°=0.8。求:
(1)滑块过B点时速度的大小;
(2)拉力F作用的时间。
答案 (1)6 m/s (2)1.5 s
解析 (1)滑块在斜面上滑行时,由牛顿第二定律得:
mgsin37°=ma3
由运动学规律可得v=2a3L
解得vB=6 m/s。
(2)撤去F前,由牛顿第二定律得:
Fcos37°-μ(mg-Fsin37°)=ma1
设F作用的时间为t,则撤去F时有:
v1=a1t,x1=a1t2
撤去拉力F后,有:μmg=ma2
v-v=2(-a2)(s-x1)
联立解得:t=1.5 s。
“牛顿运动定律的应用”章节考点归纳&典例示范
1.从受力确定运动情况
如果已知物体的受力情况,可以由牛顿第二定律求出物体的加速度,再通过运动学的规律确定物体的运动情况。
(1)从受力确定运动情况的一般求解步骤
(2)解题方法
(1)合成法:物体只受两个力的作用产生加速度时,合力的方向就是加速度的方向,解题时要求准确作出力的平行四边形,然后运用几何知识求合力F合。反之,若知道加速度方向就知道合力方向。
(2)正交分解法:当物体受到两个以上的力作用而产生加速度时,通常用正交分解法解答,一般把力正交分解为沿加速度方向和垂直于加速度方向的两个分量。即沿加速度方向:Fx=ma,垂直于加速度方向:Fy=0。
2.从运动情况确定受力
如果已知物体的运动情况,根据运动学规律求出物体的加速度,结合受力分析,再根据牛顿第二定律求出力。
从运动情况确定受力的一般求解步骤
【思考1】
加速度在解决动力学的两类问题中有什么作用?
提示:加速度是联系物体的受力情况和运动情况的桥梁,无论是已知受力情况求解运动情况,还是已知运动情况求解受力情况,都需要根据已知条件确定加速度这个桥梁。所以充分利用已知条件,确定加速度的大小和方向是解决动力学问题的关键。
【思考2】
物体的运动方向是否一定与物体所受合力的方向一致?为什么?
提示:不一定。物体的运动情况由物体所受的合力和物体的初始状态共同决定。如物体以某一初速度v0冲上光滑斜面,合力方向沿斜面向下,而物体的运动方向沿斜面向上。所以受力情况决定了加速度,但与速度没有直接关系。
【解题技巧1】
动力学两类基本问题的思维程序图如下:
由图可见,不论求解哪一类问题,加速度都是解题的桥梁和纽带,求解出加速度是顺利解答的关键。
【解题技巧2】
多过程问题的分析:
物体的多过程运动问题是牛顿运动定律应用的较难题型,它展示了物体在运动过程中的受力特点及物体的运动情况,综合考查运用动力学相关知识处理实际运动问题的能力。
解答思路:首先理清物体的不同运动过程,根据受力特点确定各过程的运动性质,然后列相应的动力学方程(运用牛顿第二定律与运动学公式);注意不同过程中的中间衔接量,特别是两过程间的“速度”参量,往往是列式与计算的“桥梁”。
若运动过程涉及摩擦力,要分析好各阶段物体所受摩擦力的大小和方向,注意摩擦力是否发生突变。
【典例示范】
1.判断正误
(1)若已知物体的受力情况,可以由运动学公式求出加速度。( )
(2)若物体所受合外力恒定,且合外力方向与物体运动方向在同一条直线上,则根据牛顿第二定律求出物体做匀变速直线运动的加速度,再根据运动学公式求速度、位移等物理量。( )
(3)若物体做匀加速直线运动,则可以根据运动学公式求出加速度,进而根据牛顿运动定律求力。( )
(4)若已知物体的运动情况,可以根据牛顿第二定律求出加速度。( )
[答案](1)× (2)√ (3)√ (4)×
2.有一质量为1 kg的小球串在长0.5 m的轻杆顶部,轻杆与水平方向的夹角为θ=37°,静止释放小球,经过0.5 s小球到达轻杆底端,g取10 m/s2,试求:
(1)小球与轻杆之间的动摩擦因数;
(2)在竖直平面内给小球施加一个垂直于轻杆方向的恒力,使小球释放后加速度为2 m/s2,此恒力大小为多少?
答案 (1)0.25 (2)8 N或24 N
解析 (1)对小球,由牛顿第二定律得
mgsinθ-μmgcosθ=ma
又x=at2
联立解得μ=0.25。
(2)若F垂直于杆向下,则mgsinθ-μ(F+mgcosθ)=ma′
解得F=8 N;
若F垂直于杆向上,则mgsinθ-μ(F-mgcosθ)=ma′
解得F=24 N。
3.某游乐园的大型“跳楼机”游戏,以惊险刺激深受年轻人的欢迎。某次游戏中,质量为m=50 kg的小明同学坐在载人平台上,并系好安全带、锁好安全杆。游戏的过程简化为巨型升降机将平台拉升100 m高度,然后由静止开始下落,在忽略空气和台架对平台阻力的情况下,该运动可近似看作自由落体运动。在下落h1=80 m时启动制动系统使平台开始做匀减速运动,再下落h2=20 m时刚好停止运动。取g=10 m/s2,求:
(1)下落的过程中小明运动速度的最大值vm;
(2)落地前20 m内,小明做匀减速直线运动的加速度a的大小;
(3)当平台落到离地面10 m高的位置时,小明对平台的压力F的大小。
答案 (1)40 m/s (2)40 m/s2 (3)2500 N
解析 (1)当下落80 m时小明的速度最大,
v=2gh1
代入数据可得:vm=40 m/s。
(2)小明做匀减速运动过程中的加速度大小为
a2=
代入数据可得:a2=40 m/s2。
(3)当平台落到离地面10 m高的位置时,小明做匀减速运动,根据牛顿第二定律:F′-mg=ma2
代入数据得:F′=2500 N
根据牛顿第三定律,小明对平台的压力F为2500 N。
4.如图所示,质量为40 kg的雪橇(包括人)在与水平方向成37°角、大小为200 N的拉力F作用下,沿水平面由静止开始运动,经过2 s撤去拉力F,雪橇与地面间的动摩擦因数为0.20。取g=10 m/s2,cos37°=0.8,sin37°=0.6。求:
(1)刚撤去拉力时雪橇的速度v的大小;
(2)撤去拉力后雪橇能继续滑行的距离x。
答案 (1)5.2 m/s (2)6.76 m
解析 (1)对雪橇,竖直方向:N1+Fsin37°=mg
水平方向:Fcos37°-f1=ma1,且f1=μN1
由运动学公式:v=a1t1
解得:v=5.2 m/s。
(2)撤去拉力后,有-μmg=ma2,
则雪橇的加速度a2=-μg
根据0-v2=2a2x,解得:x=6.76 m。
5.如图所示,长为s=11.25 m的水平轨道AB与倾角为θ=37°、长为L=3 m的光滑斜面BC在B处连接,有一质量为m=2 kg的滑块(可视为质点),从A处由静止开始受到与水平方向成37°斜向上的拉力F=20 N的作用,经过一段时间后撤去拉力F,此时滑块仍在水平轨道上,但滑块恰好可以滑到斜面的最高点C。已知滑块经过B点时,速度方向改变但大小不变,滑块与AB间的动摩擦因数μ=0.5,重力加速度g取10 m/s2,sin37°=0.6,cos37°=0.8。求:
(1)滑块过B点时速度的大小;
(2)拉力F作用的时间。
答案 (1)6 m/s (2)1.5 s
解析 (1)滑块在斜面上滑行时,由牛顿第二定律得:
mgsin37°=ma3
由运动学规律可得v=2a3L
解得vB=6 m/s。
(2)撤去F前,由牛顿第二定律得:
Fcos37°-μ(mg-Fsin37°)=ma1
设F作用的时间为t,则撤去F时有:
v1=a1t,x1=a1t2
撤去拉力F后,有:μmg=ma2
v-v=2(-a2)(s-x1)
联立解得:t=1.5 s。
