人教版(2019)必修一备考期末-《匀变速直线运动》~2.3+2.4章节巩固专练(Word含答案)
文档属性
| 名称 | 人教版(2019)必修一备考期末-《匀变速直线运动》~2.3+2.4章节巩固专练(Word含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 311.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-11-24 08:15:04 | ||
图片预览



文档简介
《匀变速直线运动》~2.3+2.4章节巩固专练
【匀变速直线运动的位移与时间关系】
A组:基础训练
1.做匀加速直线运动的物体,速度由v增加到2v时的位移为x,则当速度由3v增加到4v时,它的位移是( )
A.x B.x
C.3x D.4x
2.(多选)做匀减速直线运动的质点,它的加速度大小为a,初速度大小为v0,经过时间t速度减小到零,则它在这段时间内的位移大小可表示为( )
A.v0t+at2 B.v0t
C.v0t-at2 D.at2
3.一质点由静止开始做匀加速直线运动,它在第10 s内的位移为19 m,则其加速度大小为( )
A.1.9 m/s2 B.2.0 m/s2
C.9.5 m/s2 D.3.0 m/s2
4.一质点以一定的初速度向东做匀变速直线运动,其位移与时间的关系为:x=(10t-t2) m,则( )
A.质点初速度为10 m/s
B.质点的加速度大小是1 m/s2
C.质点的加速度大小是4 m/s2
D.在第2 s末,质点在出发点西边距出发点24 m处
5.(多选)关于关系式v2-v=2ax,下列说法正确的是( )
A.此关系式对非匀变速直线运动也适用
B.x、v0、a都是矢量,应用时必须选取统一的正方向
C.不管是加速运动还是减速运动,a都取正值
D.v0和v是初、末时刻的速度,x是这段时间内的位移
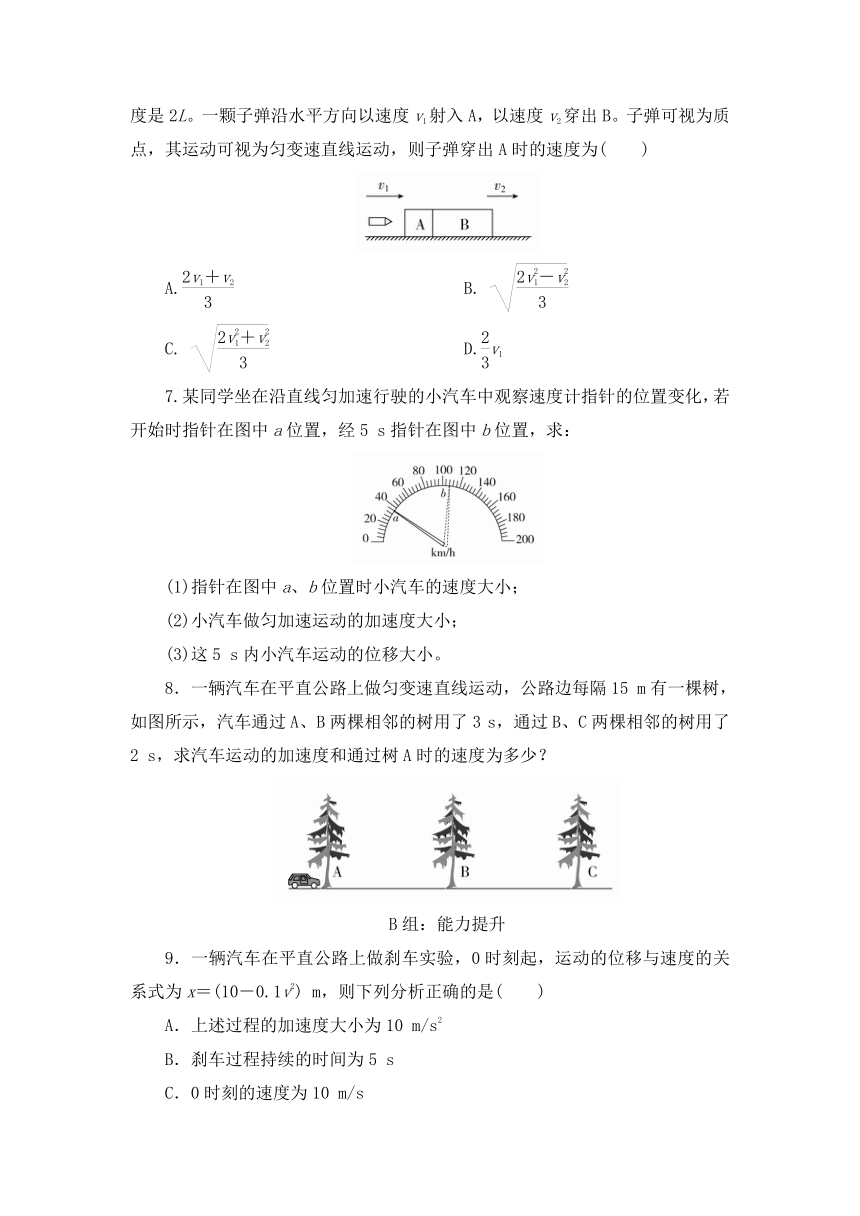
6.如图所示,木块A、B并排且固定在水平桌面上,A的长度是L,B的长度是2L。一颗子弹沿水平方向以速度v1射入A,以速度v2穿出B。子弹可视为质点,其运动可视为匀变速直线运动,则子弹穿出A时的速度为( )
A. B.
C. D.v1
7.某同学坐在沿直线匀加速行驶的小汽车中观察速度计指针的位置变化,若开始时指针在图中a位置,经5 s指针在图中b位置,求:
(1)指针在图中a、b位置时小汽车的速度大小;
(2)小汽车做匀加速运动的加速度大小;
(3)这5 s内小汽车运动的位移大小。
8.一辆汽车在平直公路上做匀变速直线运动,公路边每隔15 m有一棵树,如图所示,汽车通过A、B两棵相邻的树用了3 s,通过B、C两棵相邻的树用了2 s,求汽车运动的加速度和通过树A时的速度为多少?
B组:能力提升
9.一辆汽车在平直公路上做刹车实验,0时刻起,运动的位移与速度的关系式为x=(10-0.1v2) m,则下列分析正确的是( )
A.上述过程的加速度大小为10 m/s2
B.刹车过程持续的时间为5 s
C.0时刻的速度为10 m/s
D.刹车过程的位移为5 m
10.(综合)一辆汽车以20 m/s的速度沿平直路面行驶,当汽车以5 m/s2的加速度刹车时,则汽车在刹车后2 s内与刹车后6 s内的位移之比为( )
A.1∶1 B.3∶4 C.3∶1 D.4∶3
11.(综合)一辆汽车以10 m/s的初速度在水平地面上做匀减速直线运动,加速度大小为2 m/s2,求:
(1)汽车在2 s末的速度;
(2)汽车在6秒内的位移;
(3)汽车在最后1 s内的平均速度。
12.(综合)如图所示,杂技演员爬上高h=9 m的固定竖直竹竿,然后双腿夹紧竹竿倒立,头顶离地面高h′=7m,演员通过双腿对竹竿的压力来控制身体的运动情况,首先演员匀加速下滑3 m,速度达到v=4 m/s,然后匀减速下滑,当演员头顶刚接触地面时速度刚好减到零,求:
(1)演员匀加速下滑时的加速度大小;
(2)完成全程运动所需要的时间。
【自由落体运动】
A组:基础训练
1.(自由落体运动的特点)宇航员登上月球后,从同一高度同时由静止释放锤子和羽毛,则下落过程中( )
A.锤子比羽毛速度变化大
B.羽毛比锤子速度变化大
C.锤子的加速度比羽毛的加速度大
D.锤子和羽毛的加速度一样大
2.(比例关系)物体从某一高度自由下落,第1 s内就通过了全程的一半,物体还要下落多长时间才会落地( )
A.1 s B.1.5 s
C. s D.(-1) s
3.(自由落体运动规律的应用)一石块从地面上方h高处自由下落,当它的速度大小等于它着地速度的一半时,它距地面的高度为( )
A. B.
C. D.
4.(重力加速度)(多选)关于重力加速度的说法中,正确的是( )
A.重力加速度g是标量,只有大小没有方向,通常计算中g取9.8 m/s2
B.在地球上不同的地方,g的大小不同,但它们相差不是很大
C.在地球上同一地点,一切物体在自由落体运动中的加速度都相同
D.在地球上的同一地方,离地面高度越大重力加速度g越小
5.(物理学史)下列叙述错误的是( )
A.古希腊哲学家亚里士多德认为物体越重,下落得越快
B.伽利略发现亚里士多德的观点有自相矛盾的地方
C.伽利略认为,如果没有空气阻力,重物与轻物应该下落得同样快
D.伽利略用实验直接证实了自由落体运动是初速度为零的匀加速直线运动
6.(自由落体运动规律的应用)下列各图中,以竖直向上为正方向,其中表示物体做自由落体运动的是( )
7.(自由落体运动规律的应用)屋檐每隔0.2 s由静止落下一滴水滴,t时刻某一水滴欲下落时,刚好有两滴水滴分别位于高为1.4 m的窗户上、下沿,若不考虑其他阻力的影响,取g=10 m/s2,求:
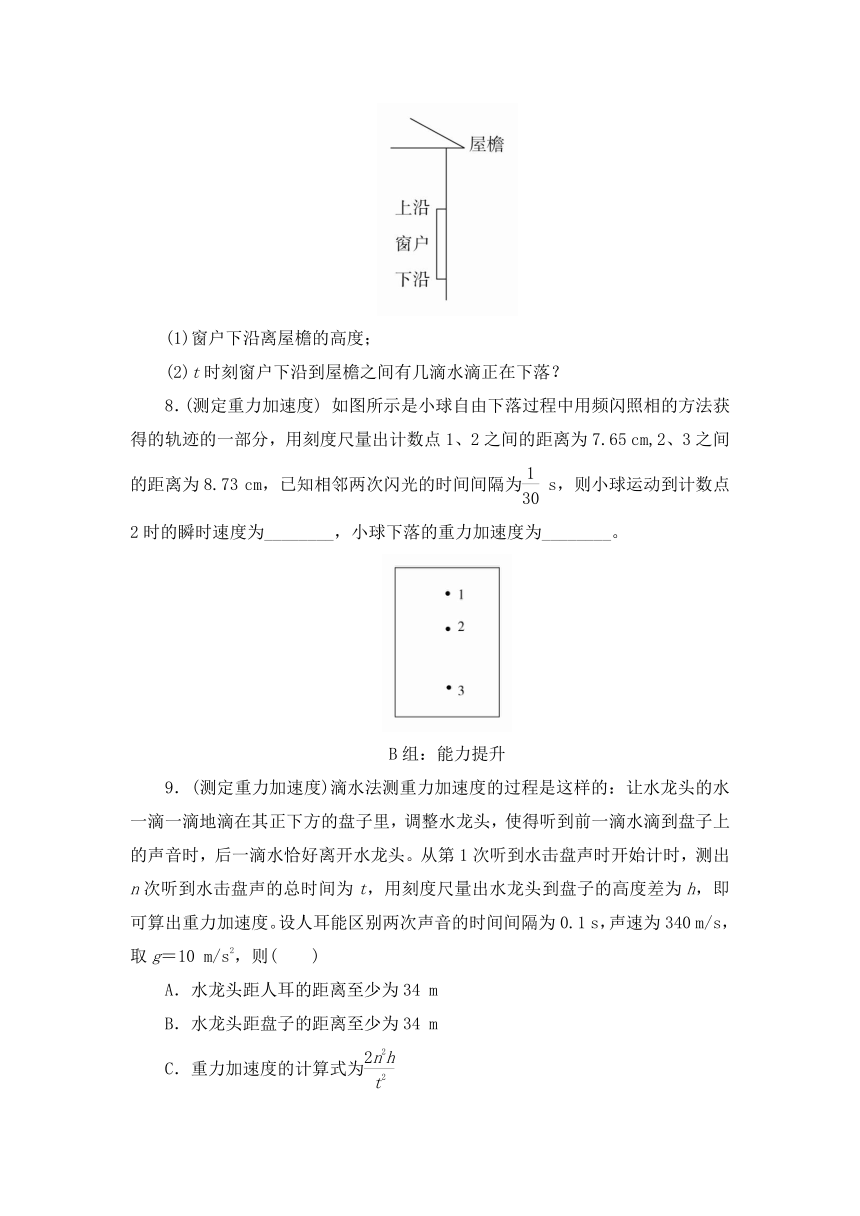
(1)窗户下沿离屋檐的高度;
(2)t时刻窗户下沿到屋檐之间有几滴水滴正在下落?
8.(测定重力加速度) 如图所示是小球自由下落过程中用频闪照相的方法获得的轨迹的一部分,用刻度尺量出计数点1、2之间的距离为7.65 cm,2、3之间的距离为8.73 cm,已知相邻两次闪光的时间间隔为 s,则小球运动到计数点2时的瞬时速度为________,小球下落的重力加速度为________。
B组:能力提升
9.(测定重力加速度)滴水法测重力加速度的过程是这样的:让水龙头的水一滴一滴地滴在其正下方的盘子里,调整水龙头,使得听到前一滴水滴到盘子上的声音时,后一滴水恰好离开水龙头。从第1次听到水击盘声时开始计时,测出n次听到水击盘声的总时间为t,用刻度尺量出水龙头到盘子的高度差为h,即可算出重力加速度。设人耳能区别两次声音的时间间隔为0.1 s,声速为340 m/s,取g=10 m/s2,则( )
A.水龙头距人耳的距离至少为34 m
B.水龙头距盘子的距离至少为34 m
C.重力加速度的计算式为
D.重力加速度的计算式为
10.(自由落体运动规律的应用)(多选)为了测出楼房的高度,让一石块从楼顶自由下落至地面(不计空气阻力,重力加速度为g),测出下列哪个物理量就可以计算出楼房的高度( )
A.石块下落到地面的总时间
B.石块下落的第1秒内的位移
C.石块落地前最后一秒内的位移
D.石块通过最后一米位移所用的时间
11.(自由落体运动规律的应用) 用如图所示的方法可以测出一个人的反应时间。甲同学用手握住直尺顶端刻度为零的地方,乙同学在直尺下端刻度为a的地方做捏住直尺的准备,但手没有碰到直尺,当乙同学看到甲同学放开直尺时,立即捏住直尺,乙同学发现捏住直尺的位置刻度为b。已知重力加速度为g,a、b的单位为国际单位制基本单位,则乙同学的反应时间t约等于( )
A. B.
C. D.
12.(综合)一名宇航员在某星球上做自由落体运动实验,让一个质量为2 kg的小球从一定的高度自由下落,测得在第5 s内的位移是18 m,则( )
A.小球在2 s末的速度是20 m/s
B.小球在第5 s内的平均速度是3.6 m/s
C.小球在5 s内的位移是50 m
D.小球在第2 s内的位移是20 m
13.(自由落体运动规律的应用)空中O点,每隔0.1 s从静止释放一相同小球,小球的体积极小,可视为质点。在连续释放几个小球后,某一瞬间拍摄的在空中运动的几个小球的照片,是按1∶40的比例拍摄的,现用刻度尺去测量照片上小球A、B、C、D之间的距离,如图。试求:
(1)小球下落的加速度多大?
(2)从照片推测,在A球上面,正在空中下落的小球有几个?
14.(测定重力加速度)某兴趣小组的同学利用自由落体运动测量当地的重力加速度,实验器材有:铁架台、光电门1和2组成的光电计时器、小球释放器(可使小球无初速度释放)、网兜、直尺、三角板。如图甲所示,实验时可用光电计时器测量小球从光电门1运动至光电门2的时间t,并用刻度尺在竖直杆上测出两光电门间的距离h。
(1)使用直尺测量小球的直径如图乙所示,则小球直径d为________ cm。
(2)保持光电门1的位置不变,改变光电门2的位置,小球经过光电门1的速度为v0,测得小球从光电门1运动至光电门2的时间为t,不考虑空气阻力,小球的加速度为重力加速度g,则两光电门间的距离h=____________(用t、g、v0表示)。
(3)根据实验数据作出 t图线,若图线斜率的绝对值为k,根据图线可求出重力加速度大小为________。
参考答案3:
1.B
2.CD
3.B
4.A
5.BD
6.C
7.
答案 (1)10 m/s 30 m/s (2)4 m/s2 (3)100 m
解析 (1)小汽车在a位置时v0=36 km/h=10 m/s;
小汽车在b位置时vt=108 km/h=30 m/s。
(2)小汽车的速度由a到b的过程有,vt=v0+at,
解得:a=4 m/s2。
(3)小汽车的速度由a到b的过程有,v-v=2ax,
解得:x=100 m。
8.
答案 1 m/s2 3.5 m/s
解析 设汽车经过A点时的速度为v0,加速度为a,对AB段运动,由位移与时间关系式得,x1=v0t1+at,
对AC段运动,由位移与时间关系式得,
x2=v0t2+at,
其中x1=15 m,x2=30 m,t1=3 s,t2=5 s,
联立两式,并代入数据得:
a=1 m/s2,v0=3.5 m/s。
9.C
10.B
11.
答案 (1)6 m/s (2)25 m (3)1 m/s
解析 (1)由v=v0+at得2 s末的速度
v=v0+at=(10-2×2) m/s=6 m/s。
(2)设汽车经过时间t0减速到停下,
则t0== s=5 s,
而t=6 s>5 s,此时汽车已停止运动。
所以6 s内的位移x=at=×2×52 m=25 m。
(3)前4 s内汽车的位移
x1=v0t1+at= m=24 m,
所以最后1 s内汽车的位移
x2=x-x1=25 m-24 m=1 m,
===1 m/s。
12.
答案 (1)2.7 m/s2 (2)3.5 s
解析 (1)设演员匀加速下滑时加速度大小为a1,下滑的高度为x1,则x1=3 m,由运动学公式有v2=2a1x1,代入数据可得a1=2.7 m/s2。
(2)设演员匀加速下滑时间为t1,匀减速下滑的加速度大小为a2,下滑时间为t2,下滑高度为x2,则由运动学公式可得,
v=a1t1,v2=2a2x2,
x2=h′-x1=7 m-3 m=4 m,
v=a2t2,t=t1+t2,
联立以上各式,并代入数据得t=3.5 s。
参考答案4:
1.D
2.D
3.C
4.BCD
5.D
6.B
7.
答案 (1)3.2 m (2)3滴
解析 (1)不考虑其他阻力的影响,水滴做自由落体运动,设水滴从开始下落到落到窗户下沿的时间为t,则另一水滴落到窗户上沿的时间为(t-0.2 s),
由题意得gt2-g(t-0.2 s)2=Δh=1.4 m,
解得t=0.8 s,
窗户下沿离屋檐的高度:H=gt2,
代入数据解得H=3.2 m。
(2)因为屋檐每隔0.2 s由静止落下一滴水滴,故0.8 s时刻窗户下沿到屋檐之间正在下落的水滴数目
n=-1=-1=3。
8.
答案 2.46 m/s 9.72 m/s2
解析 已知小球做自由落体运动,故其运动遵循匀变速直线运动的规律,所以小球运动到计数点2时的瞬时速度
v2==== m/s≈2.46 m/s。
由Δx=aT2得a=,故小球下落的重力加速度
g== m/s2=9.72 m/s2。
9.D
10.ACD
11.D
12.C
13.
答案 (1)8.0 m/s2 (2)7个
解析 (1)从图中测得AB=1.40 cm,BC=1.20 cm,CD=1.00 cm,
Δh=AB-BC=BC-CD=0.20 cm,
实际位移差为Δs=0.2×40 cm=0.080 m,
由Δs=aT2得a== m/s2=8.0 m/s2。
(2)B球此刻的速度等于下落过程中从C球此刻位置下落到A球此刻位置的平均速度,
故vB== m/s=5.20 m/s,
根据速度与时间关系式vB=atB,
代入数据得tB=0.65 s,nB==6.5个,
B球上方还有6个小球,则A球上方有7个小球,即A球上面正在空中下落的小球有7个。
14.
答案 (1)1.17 (2)v0t+gt2 (3)2k
解析 (1)由直尺读数可知,小球的直径d=2.17 cm-1.00 cm=1.17 cm。
(2)由匀变速直线运动的位移时间公式,可得:h=v0t+gt2。
(3)根据h=v0t+gt2得:=v0+gt,可知 t图线的斜率k=g,则g=2k。
【匀变速直线运动的位移与时间关系】
A组:基础训练
1.做匀加速直线运动的物体,速度由v增加到2v时的位移为x,则当速度由3v增加到4v时,它的位移是( )
A.x B.x
C.3x D.4x
2.(多选)做匀减速直线运动的质点,它的加速度大小为a,初速度大小为v0,经过时间t速度减小到零,则它在这段时间内的位移大小可表示为( )
A.v0t+at2 B.v0t
C.v0t-at2 D.at2
3.一质点由静止开始做匀加速直线运动,它在第10 s内的位移为19 m,则其加速度大小为( )
A.1.9 m/s2 B.2.0 m/s2
C.9.5 m/s2 D.3.0 m/s2
4.一质点以一定的初速度向东做匀变速直线运动,其位移与时间的关系为:x=(10t-t2) m,则( )
A.质点初速度为10 m/s
B.质点的加速度大小是1 m/s2
C.质点的加速度大小是4 m/s2
D.在第2 s末,质点在出发点西边距出发点24 m处
5.(多选)关于关系式v2-v=2ax,下列说法正确的是( )
A.此关系式对非匀变速直线运动也适用
B.x、v0、a都是矢量,应用时必须选取统一的正方向
C.不管是加速运动还是减速运动,a都取正值
D.v0和v是初、末时刻的速度,x是这段时间内的位移
6.如图所示,木块A、B并排且固定在水平桌面上,A的长度是L,B的长度是2L。一颗子弹沿水平方向以速度v1射入A,以速度v2穿出B。子弹可视为质点,其运动可视为匀变速直线运动,则子弹穿出A时的速度为( )
A. B.
C. D.v1
7.某同学坐在沿直线匀加速行驶的小汽车中观察速度计指针的位置变化,若开始时指针在图中a位置,经5 s指针在图中b位置,求:
(1)指针在图中a、b位置时小汽车的速度大小;
(2)小汽车做匀加速运动的加速度大小;
(3)这5 s内小汽车运动的位移大小。
8.一辆汽车在平直公路上做匀变速直线运动,公路边每隔15 m有一棵树,如图所示,汽车通过A、B两棵相邻的树用了3 s,通过B、C两棵相邻的树用了2 s,求汽车运动的加速度和通过树A时的速度为多少?
B组:能力提升
9.一辆汽车在平直公路上做刹车实验,0时刻起,运动的位移与速度的关系式为x=(10-0.1v2) m,则下列分析正确的是( )
A.上述过程的加速度大小为10 m/s2
B.刹车过程持续的时间为5 s
C.0时刻的速度为10 m/s
D.刹车过程的位移为5 m
10.(综合)一辆汽车以20 m/s的速度沿平直路面行驶,当汽车以5 m/s2的加速度刹车时,则汽车在刹车后2 s内与刹车后6 s内的位移之比为( )
A.1∶1 B.3∶4 C.3∶1 D.4∶3
11.(综合)一辆汽车以10 m/s的初速度在水平地面上做匀减速直线运动,加速度大小为2 m/s2,求:
(1)汽车在2 s末的速度;
(2)汽车在6秒内的位移;
(3)汽车在最后1 s内的平均速度。
12.(综合)如图所示,杂技演员爬上高h=9 m的固定竖直竹竿,然后双腿夹紧竹竿倒立,头顶离地面高h′=7m,演员通过双腿对竹竿的压力来控制身体的运动情况,首先演员匀加速下滑3 m,速度达到v=4 m/s,然后匀减速下滑,当演员头顶刚接触地面时速度刚好减到零,求:
(1)演员匀加速下滑时的加速度大小;
(2)完成全程运动所需要的时间。
【自由落体运动】
A组:基础训练
1.(自由落体运动的特点)宇航员登上月球后,从同一高度同时由静止释放锤子和羽毛,则下落过程中( )
A.锤子比羽毛速度变化大
B.羽毛比锤子速度变化大
C.锤子的加速度比羽毛的加速度大
D.锤子和羽毛的加速度一样大
2.(比例关系)物体从某一高度自由下落,第1 s内就通过了全程的一半,物体还要下落多长时间才会落地( )
A.1 s B.1.5 s
C. s D.(-1) s
3.(自由落体运动规律的应用)一石块从地面上方h高处自由下落,当它的速度大小等于它着地速度的一半时,它距地面的高度为( )
A. B.
C. D.
4.(重力加速度)(多选)关于重力加速度的说法中,正确的是( )
A.重力加速度g是标量,只有大小没有方向,通常计算中g取9.8 m/s2
B.在地球上不同的地方,g的大小不同,但它们相差不是很大
C.在地球上同一地点,一切物体在自由落体运动中的加速度都相同
D.在地球上的同一地方,离地面高度越大重力加速度g越小
5.(物理学史)下列叙述错误的是( )
A.古希腊哲学家亚里士多德认为物体越重,下落得越快
B.伽利略发现亚里士多德的观点有自相矛盾的地方
C.伽利略认为,如果没有空气阻力,重物与轻物应该下落得同样快
D.伽利略用实验直接证实了自由落体运动是初速度为零的匀加速直线运动
6.(自由落体运动规律的应用)下列各图中,以竖直向上为正方向,其中表示物体做自由落体运动的是( )
7.(自由落体运动规律的应用)屋檐每隔0.2 s由静止落下一滴水滴,t时刻某一水滴欲下落时,刚好有两滴水滴分别位于高为1.4 m的窗户上、下沿,若不考虑其他阻力的影响,取g=10 m/s2,求:
(1)窗户下沿离屋檐的高度;
(2)t时刻窗户下沿到屋檐之间有几滴水滴正在下落?
8.(测定重力加速度) 如图所示是小球自由下落过程中用频闪照相的方法获得的轨迹的一部分,用刻度尺量出计数点1、2之间的距离为7.65 cm,2、3之间的距离为8.73 cm,已知相邻两次闪光的时间间隔为 s,则小球运动到计数点2时的瞬时速度为________,小球下落的重力加速度为________。
B组:能力提升
9.(测定重力加速度)滴水法测重力加速度的过程是这样的:让水龙头的水一滴一滴地滴在其正下方的盘子里,调整水龙头,使得听到前一滴水滴到盘子上的声音时,后一滴水恰好离开水龙头。从第1次听到水击盘声时开始计时,测出n次听到水击盘声的总时间为t,用刻度尺量出水龙头到盘子的高度差为h,即可算出重力加速度。设人耳能区别两次声音的时间间隔为0.1 s,声速为340 m/s,取g=10 m/s2,则( )
A.水龙头距人耳的距离至少为34 m
B.水龙头距盘子的距离至少为34 m
C.重力加速度的计算式为
D.重力加速度的计算式为
10.(自由落体运动规律的应用)(多选)为了测出楼房的高度,让一石块从楼顶自由下落至地面(不计空气阻力,重力加速度为g),测出下列哪个物理量就可以计算出楼房的高度( )
A.石块下落到地面的总时间
B.石块下落的第1秒内的位移
C.石块落地前最后一秒内的位移
D.石块通过最后一米位移所用的时间
11.(自由落体运动规律的应用) 用如图所示的方法可以测出一个人的反应时间。甲同学用手握住直尺顶端刻度为零的地方,乙同学在直尺下端刻度为a的地方做捏住直尺的准备,但手没有碰到直尺,当乙同学看到甲同学放开直尺时,立即捏住直尺,乙同学发现捏住直尺的位置刻度为b。已知重力加速度为g,a、b的单位为国际单位制基本单位,则乙同学的反应时间t约等于( )
A. B.
C. D.
12.(综合)一名宇航员在某星球上做自由落体运动实验,让一个质量为2 kg的小球从一定的高度自由下落,测得在第5 s内的位移是18 m,则( )
A.小球在2 s末的速度是20 m/s
B.小球在第5 s内的平均速度是3.6 m/s
C.小球在5 s内的位移是50 m
D.小球在第2 s内的位移是20 m
13.(自由落体运动规律的应用)空中O点,每隔0.1 s从静止释放一相同小球,小球的体积极小,可视为质点。在连续释放几个小球后,某一瞬间拍摄的在空中运动的几个小球的照片,是按1∶40的比例拍摄的,现用刻度尺去测量照片上小球A、B、C、D之间的距离,如图。试求:
(1)小球下落的加速度多大?
(2)从照片推测,在A球上面,正在空中下落的小球有几个?
14.(测定重力加速度)某兴趣小组的同学利用自由落体运动测量当地的重力加速度,实验器材有:铁架台、光电门1和2组成的光电计时器、小球释放器(可使小球无初速度释放)、网兜、直尺、三角板。如图甲所示,实验时可用光电计时器测量小球从光电门1运动至光电门2的时间t,并用刻度尺在竖直杆上测出两光电门间的距离h。
(1)使用直尺测量小球的直径如图乙所示,则小球直径d为________ cm。
(2)保持光电门1的位置不变,改变光电门2的位置,小球经过光电门1的速度为v0,测得小球从光电门1运动至光电门2的时间为t,不考虑空气阻力,小球的加速度为重力加速度g,则两光电门间的距离h=____________(用t、g、v0表示)。
(3)根据实验数据作出 t图线,若图线斜率的绝对值为k,根据图线可求出重力加速度大小为________。
参考答案3:
1.B
2.CD
3.B
4.A
5.BD
6.C
7.
答案 (1)10 m/s 30 m/s (2)4 m/s2 (3)100 m
解析 (1)小汽车在a位置时v0=36 km/h=10 m/s;
小汽车在b位置时vt=108 km/h=30 m/s。
(2)小汽车的速度由a到b的过程有,vt=v0+at,
解得:a=4 m/s2。
(3)小汽车的速度由a到b的过程有,v-v=2ax,
解得:x=100 m。
8.
答案 1 m/s2 3.5 m/s
解析 设汽车经过A点时的速度为v0,加速度为a,对AB段运动,由位移与时间关系式得,x1=v0t1+at,
对AC段运动,由位移与时间关系式得,
x2=v0t2+at,
其中x1=15 m,x2=30 m,t1=3 s,t2=5 s,
联立两式,并代入数据得:
a=1 m/s2,v0=3.5 m/s。
9.C
10.B
11.
答案 (1)6 m/s (2)25 m (3)1 m/s
解析 (1)由v=v0+at得2 s末的速度
v=v0+at=(10-2×2) m/s=6 m/s。
(2)设汽车经过时间t0减速到停下,
则t0== s=5 s,
而t=6 s>5 s,此时汽车已停止运动。
所以6 s内的位移x=at=×2×52 m=25 m。
(3)前4 s内汽车的位移
x1=v0t1+at= m=24 m,
所以最后1 s内汽车的位移
x2=x-x1=25 m-24 m=1 m,
===1 m/s。
12.
答案 (1)2.7 m/s2 (2)3.5 s
解析 (1)设演员匀加速下滑时加速度大小为a1,下滑的高度为x1,则x1=3 m,由运动学公式有v2=2a1x1,代入数据可得a1=2.7 m/s2。
(2)设演员匀加速下滑时间为t1,匀减速下滑的加速度大小为a2,下滑时间为t2,下滑高度为x2,则由运动学公式可得,
v=a1t1,v2=2a2x2,
x2=h′-x1=7 m-3 m=4 m,
v=a2t2,t=t1+t2,
联立以上各式,并代入数据得t=3.5 s。
参考答案4:
1.D
2.D
3.C
4.BCD
5.D
6.B
7.
答案 (1)3.2 m (2)3滴
解析 (1)不考虑其他阻力的影响,水滴做自由落体运动,设水滴从开始下落到落到窗户下沿的时间为t,则另一水滴落到窗户上沿的时间为(t-0.2 s),
由题意得gt2-g(t-0.2 s)2=Δh=1.4 m,
解得t=0.8 s,
窗户下沿离屋檐的高度:H=gt2,
代入数据解得H=3.2 m。
(2)因为屋檐每隔0.2 s由静止落下一滴水滴,故0.8 s时刻窗户下沿到屋檐之间正在下落的水滴数目
n=-1=-1=3。
8.
答案 2.46 m/s 9.72 m/s2
解析 已知小球做自由落体运动,故其运动遵循匀变速直线运动的规律,所以小球运动到计数点2时的瞬时速度
v2==== m/s≈2.46 m/s。
由Δx=aT2得a=,故小球下落的重力加速度
g== m/s2=9.72 m/s2。
9.D
10.ACD
11.D
12.C
13.
答案 (1)8.0 m/s2 (2)7个
解析 (1)从图中测得AB=1.40 cm,BC=1.20 cm,CD=1.00 cm,
Δh=AB-BC=BC-CD=0.20 cm,
实际位移差为Δs=0.2×40 cm=0.080 m,
由Δs=aT2得a== m/s2=8.0 m/s2。
(2)B球此刻的速度等于下落过程中从C球此刻位置下落到A球此刻位置的平均速度,
故vB== m/s=5.20 m/s,
根据速度与时间关系式vB=atB,
代入数据得tB=0.65 s,nB==6.5个,
B球上方还有6个小球,则A球上方有7个小球,即A球上面正在空中下落的小球有7个。
14.
答案 (1)1.17 (2)v0t+gt2 (3)2k
解析 (1)由直尺读数可知,小球的直径d=2.17 cm-1.00 cm=1.17 cm。
(2)由匀变速直线运动的位移时间公式,可得:h=v0t+gt2。
(3)根据h=v0t+gt2得:=v0+gt,可知 t图线的斜率k=g,则g=2k。
