2021-2022学年鲁教版六年级数学上册3.7探索与表达规律题型分类训练(word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版六年级数学上册3.7探索与表达规律题型分类训练(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 232.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 05:48:38 | ||
图片预览



文档简介
2021-2022学年鲁教版六年级数学上册《3.7探索与表达规律》题型分类训练(附答案)
一.规律型:数字的变化类
1.1﹣2+3﹣4+5﹣6+7﹣8+…+2019﹣2020=( )
A.﹣1010 B.﹣2010 C.0 D.﹣1
2.已知一列数:a1=1,a2=3,a3=6,a4=10,…则=( )
A. B. C. D.
3.下列每个“田”字中的数据都按相同的规律排列,其最后一个“田”字中a的值为( )
A.7 B.8 C.9 D.10
4.若n1=1﹣,n2=1﹣,n3=1﹣,n4=1﹣,…,则n2020= .
5.下面每个表格中的四个数都是按相同规律填写的:
根据此规律确定x的值为 .
6.观察下列两行数:第一行:1,﹣4,9,﹣16,25,﹣36,…
第二行:4,﹣1,12,﹣13,28,﹣33,…
(1)第一排的第8个数是 ;
(2)第二排的第n个数是 .
7.将一列数:1,﹣2,3,﹣4,5,﹣6,7,﹣8……排成下列形式
按照上述规律排列下去,第10行从左边数第10个数是 .
8.古希腊数学家把数1,3,6,10,15,21,…叫做三角形数,它有一定的规律性,则第2021个三角数与第2023个三角数的差为 .
9.有一列按一定规律排列的式子:﹣3m,9m,﹣27m,81m,﹣243m,…,则第n个式子是( )
A.(﹣3)nm B.(﹣3)n+1m C.3nm D.﹣3nm
10.已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…,依此类推,则a2022的值为 .
11.阅读下列材料:小亮为了计算1+2+22+…+22017+22018+22019的值,采用以下方法:
设S=1+2+22+…+22017+22018+22019①;
则2S=2+22+23+…+22018+22019+22020②;
②﹣①得2S﹣S=(2+22+23+…+22018+22019+22020)﹣(1+2+22+…+22017+22018+22019);
∴S=2+22+23+…+22018+22019+22020﹣1﹣2﹣22﹣…﹣22017﹣22018﹣22019;
∴S=22020﹣1;
∴1+2+22+…+22017+22018+22019=22020﹣1.
请仿照小亮的方法解决以下问题:
(1)1+2+22+…+29+210= ;
(2)1+3+32+…+399= ;
(3)求1+a+a2+…+an的值(a>0,n是正整数,请写出计算过程).
12.观察下列等式:
第1个等式:×(1+)=1+;
第2个等式:×(1+)=1+;
第3个等式:×(1+)=1+;
第4个等式:×(1+)=1+;…
根据你观察到的规律,解决下列问题:
(1)写出第5个等式;
(2)写出第n个等式,并证明;
(3)计算:××××…×.
13.探索规律,观察下面算式,解答问题.
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52;
…
(1)请猜想:1+3+5+7+9+…+19= ;
(2)请猜想:1+3+5+7+9+…+(2n﹣1)+(2n+1)+(2n+3)= ;
(3)试计算:101+103+…+197+199.
14.已知13=1=×12×22,13+23=9=×22×32,13+23+33=36=×32×42,…,按照这个规律完成下列问题:
(1)13+23+33+43+53= =× 2× 2.
(2)猜想:13+23+33+…+n3= .
(3)利用(2)中的结论计算:(写出计算过程)113+123+133+143+153+163+…+393+403.
15.观察下列数:﹣1,,﹣,,﹣,……请你推测第2019个数是 ;
如果这一列数无限排列下去,与哪个数会越来越接近?
二.规律型:图形的变化类
16.如图,由等圆组成的一组图中,第1个图由1个圆组成,第2个图由5个圆组成,第3个图由11个圆组成,…,按照这样的规律排列下去,则第10个图形由( )个圆组成.
A.108 B.109 C.410 D.111
17.如图,∠MON=30°,点A1、A2、A3、A4…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A2020B2020A2021的边长为( )
A.4042 B.22019 C.4040 D.22021
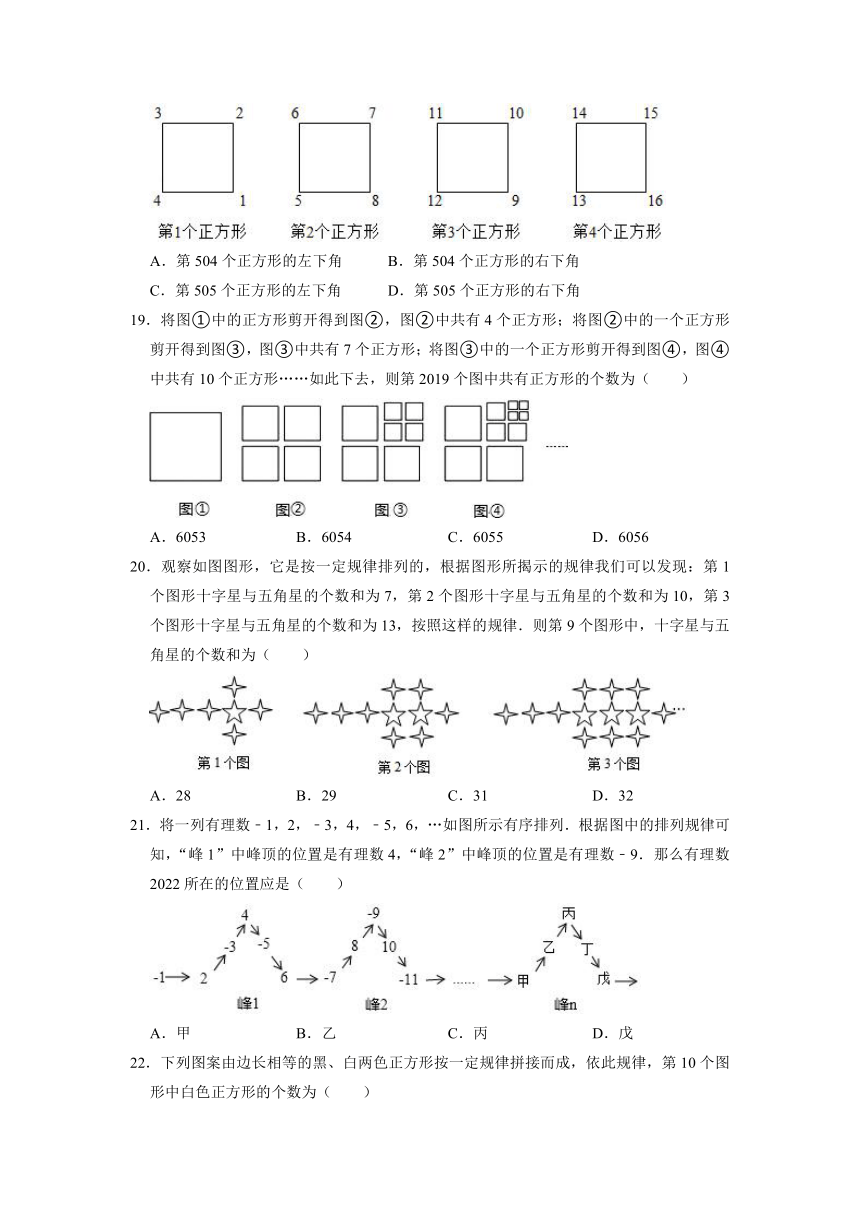
18.观察图中正方形四个顶点所标数的规律,可知2020应标在( )
A.第504个正方形的左下角 B.第504个正方形的右下角
C.第505个正方形的左下角 D.第505个正方形的右下角
19.将图①中的正方形剪开得到图②,图②中共有4个正方形;将图②中的一个正方形剪开得到图③,图③中共有7个正方形;将图③中的一个正方形剪开得到图④,图④中共有10个正方形……如此下去,则第2019个图中共有正方形的个数为( )
A.6053 B.6054 C.6055 D.6056
20.观察如图图形,它是按一定规律排列的,根据图形所揭示的规律我们可以发现:第1个图形十字星与五角星的个数和为7,第2个图形十字星与五角星的个数和为10,第3个图形十字星与五角星的个数和为13,按照这样的规律.则第9个图形中,十字星与五角星的个数和为( )
A.28 B.29 C.31 D.32
21.将一列有理数﹣1,2,﹣3,4,﹣5,6,…如图所示有序排列.根据图中的排列规律可知,“峰1”中峰顶的位置是有理数4,“峰2”中峰顶的位置是有理数﹣9.那么有理数2022所在的位置应是( )
A.甲 B.乙 C.丙 D.戊
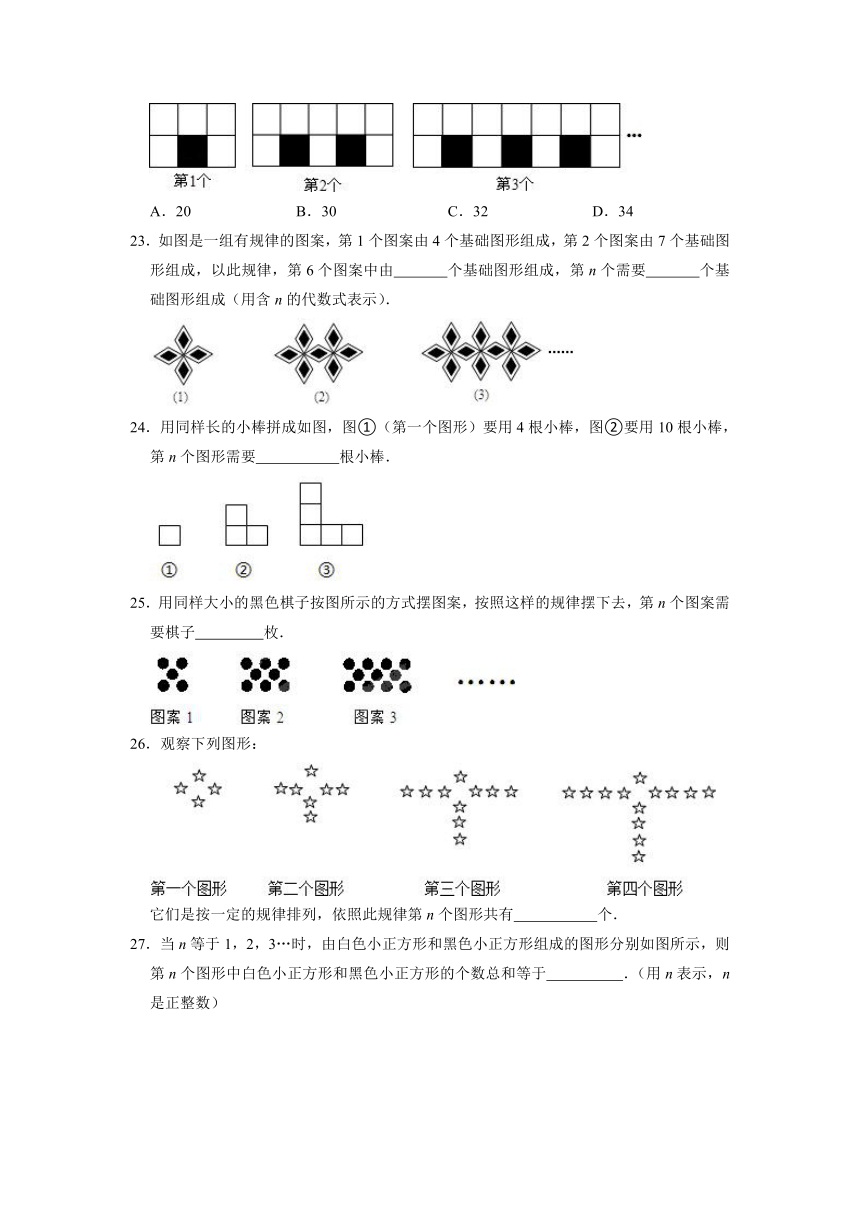
22.下列图案由边长相等的黑、白两色正方形按一定规律拼接而成,依此规律,第10个图形中白色正方形的个数为( )
A.20 B.30 C.32 D.34
23.如图是一组有规律的图案,第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,以此规律,第6个图案中由 个基础图形组成,第n个需要 个基础图形组成(用含n的代数式表示).
24.用同样长的小棒拼成如图,图①(第一个图形)要用4根小棒,图②要用10根小棒,第n个图形需要 根小棒.
25.用同样大小的黑色棋子按图所示的方式摆图案,按照这样的规律摆下去,第n个图案需要棋子 枚.
26.观察下列图形:
它们是按一定的规律排列,依照此规律第n个图形共有 个.
27.当n等于1,2,3…时,由白色小正方形和黑色小正方形组成的图形分别如图所示,则第n个图形中白色小正方形和黑色小正方形的个数总和等于 .(用n表示,n是正整数)
28.如图所示,将一个边长为1的正方形纸片分割成7个部分,部分①是边长为1的正方形纸片面积的一半,部分②是部分①面积的一半,部分⑧是部分②面积的一半,依此类推…
(1)根据图形填写下表;
① ② ③
面积
(2)阴影部分的面积是多少?
(3)猜想:①= ;
②当n=10时,请用两种方法计算:的值(结果用分数表示).
参考答案
一.规律型:数字的变化类
1.解:1﹣2+3﹣4+5﹣6+7﹣8+9﹣10+…+2019﹣2020
=(1﹣2)+(3﹣4)+(5﹣6)+…+(2019﹣2020)
=(﹣1)+(﹣1)+(﹣1)+(﹣1)+…+(﹣1)
=(﹣1)×=(﹣1)×1010
=﹣1010
故选:A.
2.解:∵a1=1,a2=3,a3=6,a4=10,…
∴++……+
=2[(1﹣)]
=2×
=.
故选:D.
3.解:由c2+1=82,可得c=9,又因为a比c小1,所以a=8.
故选:B.
4.解:n1=1﹣=,
n2=1﹣=﹣2,
n3=1﹣=,
n4=1﹣=,
…,
发现规律:
2020÷3=673…1.
则n2020=.
故答案为.
5.解:观察可知:3a=21,解得:a=7,
∴b=14,
∴x=21×14+7=301.
故答案为:301.
6.解:(1)第一行:1=12,
﹣4=﹣22,
9=32,
﹣16=﹣42,
…
发现规律:
第n个数为(﹣1)n+1n2
第8个数是﹣82=﹣64,
(2)观察第二行数,发现规律:
第二行的每个数是第一行每个数分别加3得到的.
所以第n个数(﹣1)n+1n2+3.
故答案为:﹣64、(﹣1)n+1n2+3.
7.解:根据每行的最后一个数的绝对值是这个行的行数n的平方,
所以第9行最后一个数字的绝对值是81,
第10行从左边第10个数的绝对值是81+10=91.
故第10行从左边数第10个数是﹣91.
故答案为﹣91.
8.解:第1个三角形数为1,
第2个三角形数为1+2=3,
第3个三角形数为1+2+3=6,
第4个三角形数为1+2+3+4=10,
第5个三角形数为1+2+3+4+5=15,
…
所以第2021个三角形数为1+2+3+4+…2021,
第2023个三角形数为1+2+3+4+…+2021+2022+2023,
所以第2021个三角形数与第2023个三角形数的差等于﹣2022﹣2023=﹣4045.
故答案为:﹣4045.
9.解:由﹣3m,9m,﹣27m,81m,﹣243m,…,得出规律:
系数分别是(﹣3)1,(﹣3)2,(﹣3)3,(﹣3)4,(﹣3)5,…,
字母因式均为m,
∴第n个式子是(﹣3)nm;
故选:A.
10.解:a1=0,
a2=﹣|a1+1|=|=﹣|0+1|=﹣1,
a3=﹣|a2+2|=﹣|﹣1+2|=﹣1,
a4=﹣|a3+3|=﹣|﹣1+3|=﹣2,
a5=﹣|a4+4|=﹣|﹣2+4|=﹣2,
…,
所以,n是奇数时,an=﹣(n﹣1),n是偶数时,an=﹣,
a2022=﹣=﹣1011.
故答案为:﹣1011.
11.解:(1)设S=1+2+22+……+210①,
则2S=2+22+……+211②,
②﹣①得,2S﹣S=S=211﹣1,
即S=211﹣1.
故答案为:211﹣1.
(2)设S=3+32+……+399,①
则3S=32+33+……+3100,②
②﹣①得,3S﹣S=2S=3100﹣3,
∴S=.
故答案为:.
(3)当a=1时,原式=n+1;
当a≠1时,
令S=1+a+a2+……+an,①
则aS=a+a2+……+an+1,②
②﹣①得,aS﹣S=(a﹣1)S=an+1﹣1,
∴S=.(a≠1)
综上所述:
当a=1时,原式=n+1;
当a≠1时,原式=1+a+a2+……+an=.
12.解:(1)根据已知等式可知:
第5个等式:×(1+)=1+;
(2)根据已知等式可知:
第n个等式:×(1+)=1+;
证明:左边=×==1+=右边;
(3)××××…×
=×××…×
=2×
=.
13.解:(1)1+3+5+7+9+…+19=()2=102=100,
故答案为:100;
(2)1+3+5+7+9+…+(2n﹣1)+(2n+1)+(2n+3)=()2=(n+2)2,
故答案为:(n+2)2;
(3)101+103+…+197+199
=(1+3+5+…+197+199)﹣(1+3+…+97+99)
=()2﹣()2
=1002﹣502
=7500.
14.解:(1)13+23+33+43+53=225=×52×62
(2)猜想:13+23+33+…+n3=×n2×(n+1)2
(3)利用(2)中的结论计算:
113+123+133+143+153+163+…+393+403.
解:原式=13+23+33+…+393+403﹣(13+23+33+…+103)
=×402×412﹣×102×112
=672400﹣3025
=669375
15.解:根据题意本列数为:分子为1;分母为1开始的自然数,且奇数项为负,偶数项为正,
第2019是奇数,
故应该是负数即﹣,
故答案为:﹣;
∵分母越大,分数越小,
∴这一列数无限排列下去,越来越接近0.
二.规律型:图形的变化类
16.解:根据图形的变化,发现第n个图形的最上边的一排是1个圆,第二排是2个圆,第三排是3个圆,…,第(n﹣1)排是(n﹣1)个圆,第n排是(2n﹣1)个圆;
则第n个图形的圆的个数是:
2(1+2+…n﹣1)+(2n﹣1)
=n2+n﹣1.
当n=10时,
102+10﹣1=109(个),
故选:B.
17.解:∵△A1B1A2为等边三角形,
∴∠B1A1A2=60°,
∴∠OB1A1=∠B1A1A2﹣∠MON=30°,
∴∠OB1A1=∠MON,
∴A1B1=OA1=1,
同理可得,A2B2=OA2=2,A3B3=OA3=4=22,
……
∴△A2020B2020A2021的边长=22019,
故选:B.
18.解:因为2020÷4=505,
而第505个正方形是从右下角开始计数的,
所以2020应标在左下角.
故选:C.
19.解:观察图形可知:
图②中共有4个正方形,即3×0+4;
图③中共有7个正方形,即3×1+4;
图④中共有10个正方形,即3×2+4;
……
图n中共有正方形的个数为3(n﹣2)+4;
所以第2019个图中共有正方形的个数为:
3(2019﹣2)+4=6055.
故选:C.
20.解:∵第1个图形中,十字星与五角星的个数和为6+1=7,
第2个图形中,十字星与五角星的个数和为8+2=10,
第3个图形中,十字星与五角星的个数和为10+3=13,
…
∴第9个图形中,十字星与五角星的个数和=2(2+9)+9=31.
故选:C.
21.解:因为每个峰上有5个数,每五个相邻数的位置为一个循环周期,
所以(2022﹣1)÷5=404…1
所以2022为405峰的第1个数,排在甲的位置.
故选:A.
22.解:第一个图形中有5个白色正方形;
第2个图形中有5+3×1个白色正方形;
第3个图形中有5+3×2个白色正方形;
…
第n个图形中有5+3×(n﹣1)=3n+2个白色正方形;
第10个图形中白色正方形的个数为3×10+2=32.
故选:C.
23.解:观察图形,可知
第1个图案由4个基础图形组成,即4=1×3+1,
第2个图案由7个基础图形组成,即7=2×3+1,
第3个图案由10个基础图形组成,即10=3×3+1,
…
第n个图案的基础图形数为(3n+1)个,
所以第6个图案的基础图形数是1+6×3=19.
故答案为19、3n+1.
24.解:第一个图形需要用4根小棒,
第二个图形需要用10根小棒,即10=4+6;
第三个图形需要用16根小棒,即16=4+2×6;
第四个图形需要用22根小棒,即22=4+3×6;
…
第n个图形需要4+6(n﹣1)=6n﹣2.
故答案为(6n﹣2).
25.解:根据图案可知规律如下:图2,2×3+2;图3,2×4+3…图n,2×(n+1)+n=3n+2,
故答案为:3n+2.
26.解:根据规律可知:
第一个图形中有1+1×3=4个☆,
第二个图形中有1+2×3=7个☆,
第三个图形中有1+3×3=10个☆,
…
第n个图形共有(1+3n)个☆.
故答案为:(3n+1).
27.解:第1个图形:白色正方形1个,黑色正方形4×1=4个,共有1+4=5个;
第2个图形:白色正方形22=4个,黑色正方形4×2=8个,共有4+8=12个;
第3个图形:白色正方形32=9个,黑色正方形4×3=12个,共有9+12=21个;
…,
第n个图形:白色正方形n2个,黑色正方形4n个,共有n2+4n个.
故答案为:n2+4n.
28.解:(1)观察图形可知:部分①的面积为:,
部分②的面积为=,
部分③的面积为=,
故答案为:,,;
(2)阴影部分的面积是=;
(3)①由(1)知:=1﹣,
故答案为:1﹣;
②当n=10时,
方法一:由①知:的值为:1﹣;
方法二:原式=1﹣+﹣+﹣+…+﹣=1﹣.
一.规律型:数字的变化类
1.1﹣2+3﹣4+5﹣6+7﹣8+…+2019﹣2020=( )
A.﹣1010 B.﹣2010 C.0 D.﹣1
2.已知一列数:a1=1,a2=3,a3=6,a4=10,…则=( )
A. B. C. D.
3.下列每个“田”字中的数据都按相同的规律排列,其最后一个“田”字中a的值为( )
A.7 B.8 C.9 D.10
4.若n1=1﹣,n2=1﹣,n3=1﹣,n4=1﹣,…,则n2020= .
5.下面每个表格中的四个数都是按相同规律填写的:
根据此规律确定x的值为 .
6.观察下列两行数:第一行:1,﹣4,9,﹣16,25,﹣36,…
第二行:4,﹣1,12,﹣13,28,﹣33,…
(1)第一排的第8个数是 ;
(2)第二排的第n个数是 .
7.将一列数:1,﹣2,3,﹣4,5,﹣6,7,﹣8……排成下列形式
按照上述规律排列下去,第10行从左边数第10个数是 .
8.古希腊数学家把数1,3,6,10,15,21,…叫做三角形数,它有一定的规律性,则第2021个三角数与第2023个三角数的差为 .
9.有一列按一定规律排列的式子:﹣3m,9m,﹣27m,81m,﹣243m,…,则第n个式子是( )
A.(﹣3)nm B.(﹣3)n+1m C.3nm D.﹣3nm
10.已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…,依此类推,则a2022的值为 .
11.阅读下列材料:小亮为了计算1+2+22+…+22017+22018+22019的值,采用以下方法:
设S=1+2+22+…+22017+22018+22019①;
则2S=2+22+23+…+22018+22019+22020②;
②﹣①得2S﹣S=(2+22+23+…+22018+22019+22020)﹣(1+2+22+…+22017+22018+22019);
∴S=2+22+23+…+22018+22019+22020﹣1﹣2﹣22﹣…﹣22017﹣22018﹣22019;
∴S=22020﹣1;
∴1+2+22+…+22017+22018+22019=22020﹣1.
请仿照小亮的方法解决以下问题:
(1)1+2+22+…+29+210= ;
(2)1+3+32+…+399= ;
(3)求1+a+a2+…+an的值(a>0,n是正整数,请写出计算过程).
12.观察下列等式:
第1个等式:×(1+)=1+;
第2个等式:×(1+)=1+;
第3个等式:×(1+)=1+;
第4个等式:×(1+)=1+;…
根据你观察到的规律,解决下列问题:
(1)写出第5个等式;
(2)写出第n个等式,并证明;
(3)计算:××××…×.
13.探索规律,观察下面算式,解答问题.
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52;
…
(1)请猜想:1+3+5+7+9+…+19= ;
(2)请猜想:1+3+5+7+9+…+(2n﹣1)+(2n+1)+(2n+3)= ;
(3)试计算:101+103+…+197+199.
14.已知13=1=×12×22,13+23=9=×22×32,13+23+33=36=×32×42,…,按照这个规律完成下列问题:
(1)13+23+33+43+53= =× 2× 2.
(2)猜想:13+23+33+…+n3= .
(3)利用(2)中的结论计算:(写出计算过程)113+123+133+143+153+163+…+393+403.
15.观察下列数:﹣1,,﹣,,﹣,……请你推测第2019个数是 ;
如果这一列数无限排列下去,与哪个数会越来越接近?
二.规律型:图形的变化类
16.如图,由等圆组成的一组图中,第1个图由1个圆组成,第2个图由5个圆组成,第3个图由11个圆组成,…,按照这样的规律排列下去,则第10个图形由( )个圆组成.
A.108 B.109 C.410 D.111
17.如图,∠MON=30°,点A1、A2、A3、A4…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A2020B2020A2021的边长为( )
A.4042 B.22019 C.4040 D.22021
18.观察图中正方形四个顶点所标数的规律,可知2020应标在( )
A.第504个正方形的左下角 B.第504个正方形的右下角
C.第505个正方形的左下角 D.第505个正方形的右下角
19.将图①中的正方形剪开得到图②,图②中共有4个正方形;将图②中的一个正方形剪开得到图③,图③中共有7个正方形;将图③中的一个正方形剪开得到图④,图④中共有10个正方形……如此下去,则第2019个图中共有正方形的个数为( )
A.6053 B.6054 C.6055 D.6056
20.观察如图图形,它是按一定规律排列的,根据图形所揭示的规律我们可以发现:第1个图形十字星与五角星的个数和为7,第2个图形十字星与五角星的个数和为10,第3个图形十字星与五角星的个数和为13,按照这样的规律.则第9个图形中,十字星与五角星的个数和为( )
A.28 B.29 C.31 D.32
21.将一列有理数﹣1,2,﹣3,4,﹣5,6,…如图所示有序排列.根据图中的排列规律可知,“峰1”中峰顶的位置是有理数4,“峰2”中峰顶的位置是有理数﹣9.那么有理数2022所在的位置应是( )
A.甲 B.乙 C.丙 D.戊
22.下列图案由边长相等的黑、白两色正方形按一定规律拼接而成,依此规律,第10个图形中白色正方形的个数为( )
A.20 B.30 C.32 D.34
23.如图是一组有规律的图案,第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,以此规律,第6个图案中由 个基础图形组成,第n个需要 个基础图形组成(用含n的代数式表示).
24.用同样长的小棒拼成如图,图①(第一个图形)要用4根小棒,图②要用10根小棒,第n个图形需要 根小棒.
25.用同样大小的黑色棋子按图所示的方式摆图案,按照这样的规律摆下去,第n个图案需要棋子 枚.
26.观察下列图形:
它们是按一定的规律排列,依照此规律第n个图形共有 个.
27.当n等于1,2,3…时,由白色小正方形和黑色小正方形组成的图形分别如图所示,则第n个图形中白色小正方形和黑色小正方形的个数总和等于 .(用n表示,n是正整数)
28.如图所示,将一个边长为1的正方形纸片分割成7个部分,部分①是边长为1的正方形纸片面积的一半,部分②是部分①面积的一半,部分⑧是部分②面积的一半,依此类推…
(1)根据图形填写下表;
① ② ③
面积
(2)阴影部分的面积是多少?
(3)猜想:①= ;
②当n=10时,请用两种方法计算:的值(结果用分数表示).
参考答案
一.规律型:数字的变化类
1.解:1﹣2+3﹣4+5﹣6+7﹣8+9﹣10+…+2019﹣2020
=(1﹣2)+(3﹣4)+(5﹣6)+…+(2019﹣2020)
=(﹣1)+(﹣1)+(﹣1)+(﹣1)+…+(﹣1)
=(﹣1)×=(﹣1)×1010
=﹣1010
故选:A.
2.解:∵a1=1,a2=3,a3=6,a4=10,…
∴++……+
=2[(1﹣)]
=2×
=.
故选:D.
3.解:由c2+1=82,可得c=9,又因为a比c小1,所以a=8.
故选:B.
4.解:n1=1﹣=,
n2=1﹣=﹣2,
n3=1﹣=,
n4=1﹣=,
…,
发现规律:
2020÷3=673…1.
则n2020=.
故答案为.
5.解:观察可知:3a=21,解得:a=7,
∴b=14,
∴x=21×14+7=301.
故答案为:301.
6.解:(1)第一行:1=12,
﹣4=﹣22,
9=32,
﹣16=﹣42,
…
发现规律:
第n个数为(﹣1)n+1n2
第8个数是﹣82=﹣64,
(2)观察第二行数,发现规律:
第二行的每个数是第一行每个数分别加3得到的.
所以第n个数(﹣1)n+1n2+3.
故答案为:﹣64、(﹣1)n+1n2+3.
7.解:根据每行的最后一个数的绝对值是这个行的行数n的平方,
所以第9行最后一个数字的绝对值是81,
第10行从左边第10个数的绝对值是81+10=91.
故第10行从左边数第10个数是﹣91.
故答案为﹣91.
8.解:第1个三角形数为1,
第2个三角形数为1+2=3,
第3个三角形数为1+2+3=6,
第4个三角形数为1+2+3+4=10,
第5个三角形数为1+2+3+4+5=15,
…
所以第2021个三角形数为1+2+3+4+…2021,
第2023个三角形数为1+2+3+4+…+2021+2022+2023,
所以第2021个三角形数与第2023个三角形数的差等于﹣2022﹣2023=﹣4045.
故答案为:﹣4045.
9.解:由﹣3m,9m,﹣27m,81m,﹣243m,…,得出规律:
系数分别是(﹣3)1,(﹣3)2,(﹣3)3,(﹣3)4,(﹣3)5,…,
字母因式均为m,
∴第n个式子是(﹣3)nm;
故选:A.
10.解:a1=0,
a2=﹣|a1+1|=|=﹣|0+1|=﹣1,
a3=﹣|a2+2|=﹣|﹣1+2|=﹣1,
a4=﹣|a3+3|=﹣|﹣1+3|=﹣2,
a5=﹣|a4+4|=﹣|﹣2+4|=﹣2,
…,
所以,n是奇数时,an=﹣(n﹣1),n是偶数时,an=﹣,
a2022=﹣=﹣1011.
故答案为:﹣1011.
11.解:(1)设S=1+2+22+……+210①,
则2S=2+22+……+211②,
②﹣①得,2S﹣S=S=211﹣1,
即S=211﹣1.
故答案为:211﹣1.
(2)设S=3+32+……+399,①
则3S=32+33+……+3100,②
②﹣①得,3S﹣S=2S=3100﹣3,
∴S=.
故答案为:.
(3)当a=1时,原式=n+1;
当a≠1时,
令S=1+a+a2+……+an,①
则aS=a+a2+……+an+1,②
②﹣①得,aS﹣S=(a﹣1)S=an+1﹣1,
∴S=.(a≠1)
综上所述:
当a=1时,原式=n+1;
当a≠1时,原式=1+a+a2+……+an=.
12.解:(1)根据已知等式可知:
第5个等式:×(1+)=1+;
(2)根据已知等式可知:
第n个等式:×(1+)=1+;
证明:左边=×==1+=右边;
(3)××××…×
=×××…×
=2×
=.
13.解:(1)1+3+5+7+9+…+19=()2=102=100,
故答案为:100;
(2)1+3+5+7+9+…+(2n﹣1)+(2n+1)+(2n+3)=()2=(n+2)2,
故答案为:(n+2)2;
(3)101+103+…+197+199
=(1+3+5+…+197+199)﹣(1+3+…+97+99)
=()2﹣()2
=1002﹣502
=7500.
14.解:(1)13+23+33+43+53=225=×52×62
(2)猜想:13+23+33+…+n3=×n2×(n+1)2
(3)利用(2)中的结论计算:
113+123+133+143+153+163+…+393+403.
解:原式=13+23+33+…+393+403﹣(13+23+33+…+103)
=×402×412﹣×102×112
=672400﹣3025
=669375
15.解:根据题意本列数为:分子为1;分母为1开始的自然数,且奇数项为负,偶数项为正,
第2019是奇数,
故应该是负数即﹣,
故答案为:﹣;
∵分母越大,分数越小,
∴这一列数无限排列下去,越来越接近0.
二.规律型:图形的变化类
16.解:根据图形的变化,发现第n个图形的最上边的一排是1个圆,第二排是2个圆,第三排是3个圆,…,第(n﹣1)排是(n﹣1)个圆,第n排是(2n﹣1)个圆;
则第n个图形的圆的个数是:
2(1+2+…n﹣1)+(2n﹣1)
=n2+n﹣1.
当n=10时,
102+10﹣1=109(个),
故选:B.
17.解:∵△A1B1A2为等边三角形,
∴∠B1A1A2=60°,
∴∠OB1A1=∠B1A1A2﹣∠MON=30°,
∴∠OB1A1=∠MON,
∴A1B1=OA1=1,
同理可得,A2B2=OA2=2,A3B3=OA3=4=22,
……
∴△A2020B2020A2021的边长=22019,
故选:B.
18.解:因为2020÷4=505,
而第505个正方形是从右下角开始计数的,
所以2020应标在左下角.
故选:C.
19.解:观察图形可知:
图②中共有4个正方形,即3×0+4;
图③中共有7个正方形,即3×1+4;
图④中共有10个正方形,即3×2+4;
……
图n中共有正方形的个数为3(n﹣2)+4;
所以第2019个图中共有正方形的个数为:
3(2019﹣2)+4=6055.
故选:C.
20.解:∵第1个图形中,十字星与五角星的个数和为6+1=7,
第2个图形中,十字星与五角星的个数和为8+2=10,
第3个图形中,十字星与五角星的个数和为10+3=13,
…
∴第9个图形中,十字星与五角星的个数和=2(2+9)+9=31.
故选:C.
21.解:因为每个峰上有5个数,每五个相邻数的位置为一个循环周期,
所以(2022﹣1)÷5=404…1
所以2022为405峰的第1个数,排在甲的位置.
故选:A.
22.解:第一个图形中有5个白色正方形;
第2个图形中有5+3×1个白色正方形;
第3个图形中有5+3×2个白色正方形;
…
第n个图形中有5+3×(n﹣1)=3n+2个白色正方形;
第10个图形中白色正方形的个数为3×10+2=32.
故选:C.
23.解:观察图形,可知
第1个图案由4个基础图形组成,即4=1×3+1,
第2个图案由7个基础图形组成,即7=2×3+1,
第3个图案由10个基础图形组成,即10=3×3+1,
…
第n个图案的基础图形数为(3n+1)个,
所以第6个图案的基础图形数是1+6×3=19.
故答案为19、3n+1.
24.解:第一个图形需要用4根小棒,
第二个图形需要用10根小棒,即10=4+6;
第三个图形需要用16根小棒,即16=4+2×6;
第四个图形需要用22根小棒,即22=4+3×6;
…
第n个图形需要4+6(n﹣1)=6n﹣2.
故答案为(6n﹣2).
25.解:根据图案可知规律如下:图2,2×3+2;图3,2×4+3…图n,2×(n+1)+n=3n+2,
故答案为:3n+2.
26.解:根据规律可知:
第一个图形中有1+1×3=4个☆,
第二个图形中有1+2×3=7个☆,
第三个图形中有1+3×3=10个☆,
…
第n个图形共有(1+3n)个☆.
故答案为:(3n+1).
27.解:第1个图形:白色正方形1个,黑色正方形4×1=4个,共有1+4=5个;
第2个图形:白色正方形22=4个,黑色正方形4×2=8个,共有4+8=12个;
第3个图形:白色正方形32=9个,黑色正方形4×3=12个,共有9+12=21个;
…,
第n个图形:白色正方形n2个,黑色正方形4n个,共有n2+4n个.
故答案为:n2+4n.
28.解:(1)观察图形可知:部分①的面积为:,
部分②的面积为=,
部分③的面积为=,
故答案为:,,;
(2)阴影部分的面积是=;
(3)①由(1)知:=1﹣,
故答案为:1﹣;
②当n=10时,
方法一:由①知:的值为:1﹣;
方法二:原式=1﹣+﹣+﹣+…+﹣=1﹣.
