2021-2022学年鲁教版(五四制)九年级数学下册5.9弧长及扇形的面积 知识点分类练习(word解析版)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)九年级数学下册5.9弧长及扇形的面积 知识点分类练习(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 311.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 06:00:49 | ||
图片预览

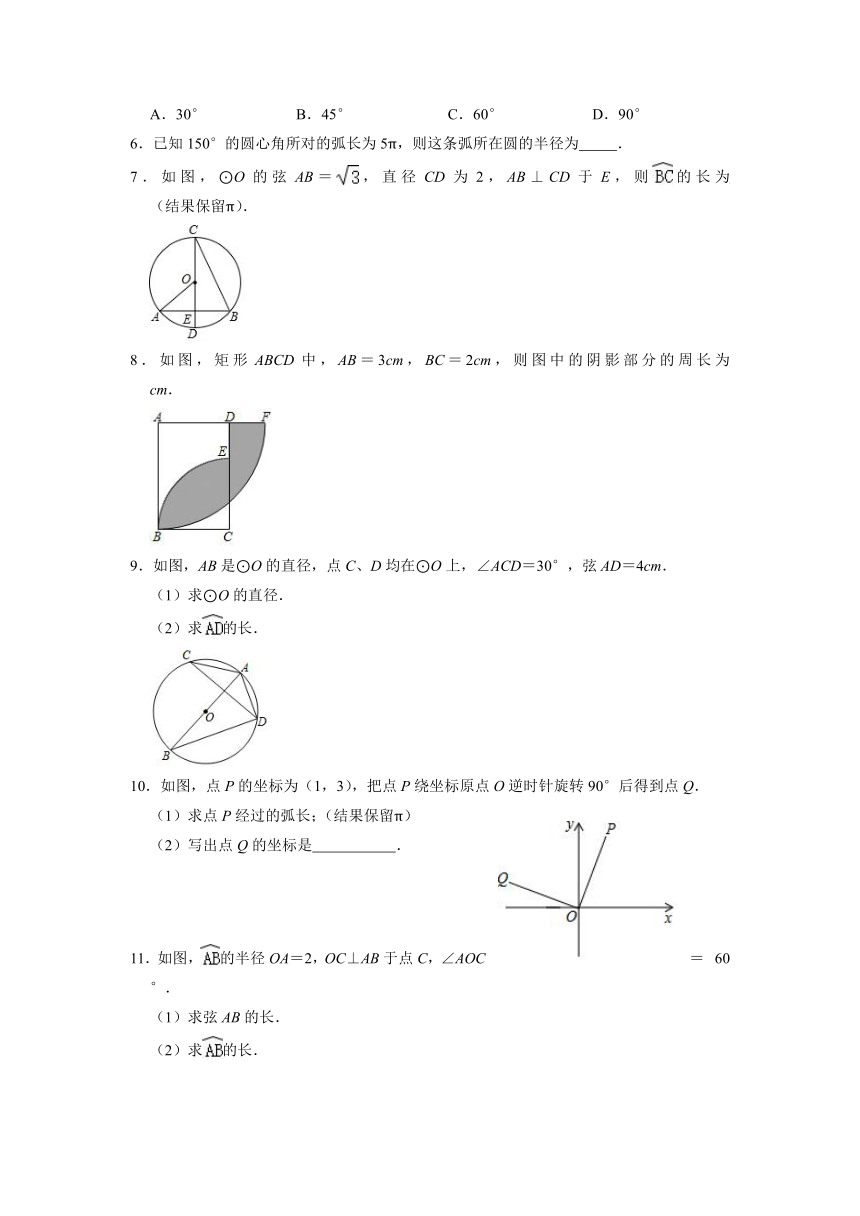
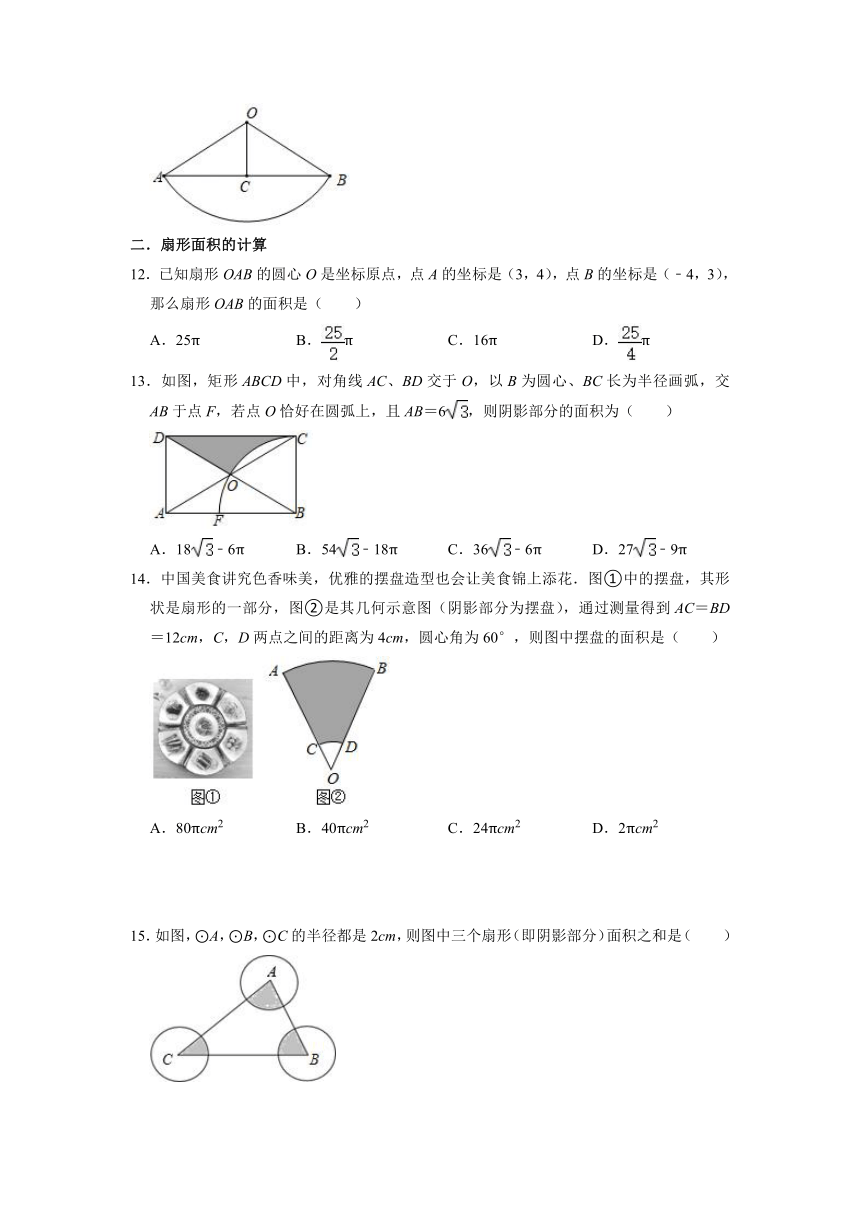


文档简介
2021-2022学年鲁教版九年级数学下册《5.9弧长及扇形的面积》知识点分类练习(附答案)
一.弧长的计算
1.如图,圆上有A、B、C、D四点,其中∠BAD=80°,若弧ABC、弧ADC的长度分别为7π、11π,则弧BAD的长度是( )
A.4π B.8π C.10π D.15π
2.下列说法正确的是( )
A.的倒数是 B.计算弧长的公式是
C.1是最小的自然数 D.1的因数只有1个
3.在平面直角坐标系中,若干个半径为1个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,向右沿这条曲线做上下起伏运动(如图),点P在直线上运动的速度为每秒1个单位长度.点P在弧线上运动的速度为每秒个单位长度,则2019秒时,点P的坐标是( )
A.(,) B.(,﹣)
C.(2019,) D.(2019,﹣)
4.如图,在⊙O中,弦BC=1,点A是圆上一点,且∠BAC=30°,则劣弧的长是( )
A.π B. C. D.
5.如果一个扇形的半径是2,弧长是,则此扇形的圆心角的度数为( )
A.30° B.45° C.60° D.90°
6.已知150°的圆心角所对的弧长为5π,则这条弧所在圆的半径为 .
7.如图,⊙O的弦AB=,直径CD为2,AB⊥CD于E,则的长为 (结果保留π).
8.如图,矩形ABCD中,AB=3cm,BC=2cm,则图中的阴影部分的周长为 cm.
9.如图,AB是⊙O的直径,点C、D均在⊙O上,∠ACD=30°,弦AD=4cm.
(1)求⊙O的直径.
(2)求的长.
10.如图,点P的坐标为(1,3),把点P绕坐标原点O逆时针旋转90°后得到点Q.
(1)求点P经过的弧长;(结果保留π)
(2)写出点Q的坐标是 .
11.如图,的半径OA=2,OC⊥AB于点C,∠AOC=60°.
(1)求弦AB的长.
(2)求的长.
二.扇形面积的计算
12.已知扇形OAB的圆心O是坐标原点,点A的坐标是(3,4),点B的坐标是(﹣4,3),那么扇形OAB的面积是( )
A.25π B.π C.16π D.π
13.如图,矩形ABCD中,对角线AC、BD交于O,以B为圆心、BC长为半径画弧,交AB于点F,若点O恰好在圆弧上,且AB=6,则阴影部分的面积为( )
A.18﹣6π B.54﹣18π C.36﹣6π D.27﹣9π
14.中国美食讲究色香味美,优雅的摆盘造型也会让美食锦上添花.图①中的摆盘,其形状是扇形的一部分,图②是其几何示意图(阴影部分为摆盘),通过测量得到AC=BD=12cm,C,D两点之间的距离为4cm,圆心角为60°,则图中摆盘的面积是( )
A.80πcm2 B.40πcm2 C.24πcm2 D.2πcm2
15.如图,⊙A,⊙B,⊙C的半径都是2cm,则图中三个扇形(即阴影部分)面积之和是( )
A.2π B.π C. D.6π
16.如图,在扇形OAB中,已知∠AOB=90°,OA=,过的中点C作CD⊥OA,CE⊥OB,垂足分别为D、E,则图中阴影部分的面积为( )
A.π﹣1 B.﹣1 C.π﹣ D.﹣
17.如图,在△ABC中,∠C=90°,∠BAC=60°,AC=2,将△ABC绕点A顺时针旋转45°,得到△AB'C',B'C'与AB相交于点D,则图中阴影部分的面积为 .
18.如图,平行四边形ABCD中,∠A=60°,CD=4,以点A为圆心,AB的长为半径画弧交AD边于点E,以点B为圆心,BE的长为半径画弧交BC边于点F,则阴影部分的面积为 .
19.如图,AB是⊙O的弦,直线BC与⊙O相切于点B,AD⊥BC,垂足为D,连接OA,OB.
(1)求证:AB平分∠OAD;
(2)当∠AOB=100°,⊙O的半径为6cm时.
①直接写出扇形AOB的面积约为 cm2(结果精确到1cm2);
②点E是⊙O上一动点(点E不与点A、点B重合),连接AE,BE,请直接写出∠AEB= °.
20.如图,半圆O的直径AB=20,将半圆O绕点B顺时针旋转45°得到半圆O′,与AB交于点P.
(1)求AP的长;
(2)求图中阴影部分的面积(结果保留π).
参考答案
一.弧长的计算
1.解:∵、的长度分别为7π,11π,
∴圆的周长为18π,
∵∠A=80°,
∴∠C=180°﹣80°=100°,
故=×18π=10π.
故选:C.
2.解:A,1的倒数是,所以1的倒数是是错误的.
B,因为弧长公式:I=,所以计算弧长的公式是是错误的.
C,因为最小的自然数是0,所以所以1是最小的自然数,说法错误.
D,一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身.1的因数只有1.说法正确.
故选:D.
3.解:设第n秒运动到Pn(n为自然数)点,
观察,发现规律:P1(,),P2(1,0),P3(,﹣),P4(2,0),P5(,),…,
∴P4n+1(,),P4n+2(n+1,0),P4n+3(,﹣),P4n+4(2n+2,0).
∵2019=4×504+3,
∴P2019为(,﹣),
故选:B.
4.解:连接OB,OC.
∵∠BOC=2∠BAC=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴OB=OC=BC=1,
∴劣弧的长==,
故选:B.
5.解:∵扇形的弧长为,半径为2,
∴=,
解得:n=45°.
故选:B.
6.解:设这条弧所在圆的半径为R,
由题意得,=5π,
解得,R=6,
故答案为:6.
7.解:连接OB,
∵AB=,CD是⊙O的直径,
∴BE=AB=,
∵OB=CD=1,
∴sin∠DOB==,
∴∠DOB=60°,
∴∠BOC=120°,
∴的长为=π,
故答案为:π.
8.解:由图可知,
阴影部分的周长是:(3﹣2)+(3﹣2)=+2=(+2)cm,
故答案为:(+2).
9.解:(1)∵AB是⊙O的直径,
∴∠ADB=90°.
∵同弧所对的圆周角相等,
∴∠ABD=∠ACD=30°.
∵AD=4,
∴AB=8.
∴⊙O的直径为8cm.
(2)连接OD,则∠AOD=2∠ACD=60°.
∴的长为.
10.解:(1)如图,过P作PA⊥x轴于A,
∵P(1,3),
∴,
∴点P经过的弧长为;
(2)把点P绕坐标原点O逆时针旋转90°后得到点Q,过点P作x轴的垂线,垂足是B,
∴OQ=PO,∠POQ=90°,
∴∠POA+∠QOB=90°,∠QOB=∠OPA,△QOB≌△OPA(AAS),
∴OB=PA=3,BQ=AO=1,
则点Q的坐标是(﹣3,1).
故答案是:(﹣3,1).
11.解:(1)∵的半径OA=2,OC⊥AB于点C,∠AOC=60°,
∴AC=OA sin60°=2×=,
∴AB=2AC=2;
(2)∵OC⊥AB,∠AOC=60°,
∴∠AOB=120°,
∵OA=2,
∴的长是:=.
二.扇形面积的计算
12.解:∵点A的坐标是(3,4),点B的坐标是(﹣4,3),
∴∠AOB=90°,OA=OB==5,
∴扇形OAB的面积==π,
故选:D.
13.解:∵四边形ABCD是矩形,
∴AB=CD=6,∠DCB=90°,AC=BD,OC=AC,OB=BD,
∴OB=OC,
∵BC=OB,
∴△OBC是等边三角形,
∴∠CBO=60°,BC=BO,
即AC=2BC,
在Rt△ABC中,由勾股定理得:AB2+BC2=AC2,
(6)2+BC2=(2BC)2,
解得:BC=6,
∴阴影部分的面积=S△BCD﹣S扇形BOC=﹣=18﹣6π,
故选:A.
14.解:如图,连接CD.
∵OC=OD,∠O=60°,
∴△COD是等边三角形,
∴OC=OD=CD=4cm,
∴S阴=S扇形OAB﹣S扇形OCD=﹣=40π(cm2),
故选:B.
15.解:∵∠A+∠B+∠C=180°,
∴阴影部分的面积==2π.
故选:A.
16.解:∵CD⊥OA,CE⊥OB,
∴∠CDO=∠CEO=∠AOB=90°,
∴四边形CDOE是矩形,
连接OC,
∵点C是的中点,
∴∠AOC=∠BOC,
∵OC=OC,
∴△COD≌△COE(AAS),
∴OD=OE,
∴矩形CDOE是正方形,
∵OC=OA=,
∴OE=1,
∴图中阴影部分的面积=﹣1×1=﹣1,
故选:B.
17.解:∵在△ABC中,∠C=90°,∠BAC=60°,AC=2,
∴AB=2AC=4,∠ABC=30°,
过D作DH⊥AB′于H,
∵将△ABC绕点A顺时针旋转45°,得到△AB'C',
∴AB′=AB=4,∠AB′C′=∠ABC=30°,∠BAB′=45°,AC′=AC=2,
设DH=AH=x,
∴B′H=DH=x,
∴AH+B′H=x+x=AB′=4,
∴x=2(﹣1),
∴B′D=2DH=4(﹣1),
∴图中阴影部分的面积=S扇形BAB′﹣S△ADB′=﹣=2π﹣4(﹣1),
故答案为:2π﹣4(﹣1).
18.解:如图连接BE,EF.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠ABC=180°,
∵∠A=60°,
∴∠ABC=120°,
∵AE=AB,
∴△ABE是等边三角形,
∴∠ABE=∠EBF=60°,
∵BE=BF,
∴△EBF是等边三角形,
∵S阴=S△BEF=×42=4,
故答案为4.
19.(1)证明:∵OA=OB,
∴∠OBA=∠OAB,
∵OB⊥CB,AD⊥BC,
∴OB∥AD,
∴∠OBA=∠DAB,
∴∠OAB=∠DAB,
∴AB平分∠OAD;
(2)①∵∠AOB=100°,⊙O的半径为6cm,
∴扇形AOB的面积为:≈31(cm2),
故答案为:31;
②当点E在优弧AB上时,
∵∠AOB=100°,
∴∠AEB=50°,
当点E在劣弧AB上时,
∠AEB=180°﹣50°=130°,
故答案为:50或130.
20.解:(1)∵∠OBA′=45°,O′P=O′B,
∴△O′PB是等腰直角三角形,
∴PB=BO,
∴AP=AB﹣BP=20﹣10;
(2)阴影部分面积为:
S阴影=S扇形O′A′P+S△O′PB=×π×100+10×10×=25π+50.
一.弧长的计算
1.如图,圆上有A、B、C、D四点,其中∠BAD=80°,若弧ABC、弧ADC的长度分别为7π、11π,则弧BAD的长度是( )
A.4π B.8π C.10π D.15π
2.下列说法正确的是( )
A.的倒数是 B.计算弧长的公式是
C.1是最小的自然数 D.1的因数只有1个
3.在平面直角坐标系中,若干个半径为1个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,向右沿这条曲线做上下起伏运动(如图),点P在直线上运动的速度为每秒1个单位长度.点P在弧线上运动的速度为每秒个单位长度,则2019秒时,点P的坐标是( )
A.(,) B.(,﹣)
C.(2019,) D.(2019,﹣)
4.如图,在⊙O中,弦BC=1,点A是圆上一点,且∠BAC=30°,则劣弧的长是( )
A.π B. C. D.
5.如果一个扇形的半径是2,弧长是,则此扇形的圆心角的度数为( )
A.30° B.45° C.60° D.90°
6.已知150°的圆心角所对的弧长为5π,则这条弧所在圆的半径为 .
7.如图,⊙O的弦AB=,直径CD为2,AB⊥CD于E,则的长为 (结果保留π).
8.如图,矩形ABCD中,AB=3cm,BC=2cm,则图中的阴影部分的周长为 cm.
9.如图,AB是⊙O的直径,点C、D均在⊙O上,∠ACD=30°,弦AD=4cm.
(1)求⊙O的直径.
(2)求的长.
10.如图,点P的坐标为(1,3),把点P绕坐标原点O逆时针旋转90°后得到点Q.
(1)求点P经过的弧长;(结果保留π)
(2)写出点Q的坐标是 .
11.如图,的半径OA=2,OC⊥AB于点C,∠AOC=60°.
(1)求弦AB的长.
(2)求的长.
二.扇形面积的计算
12.已知扇形OAB的圆心O是坐标原点,点A的坐标是(3,4),点B的坐标是(﹣4,3),那么扇形OAB的面积是( )
A.25π B.π C.16π D.π
13.如图,矩形ABCD中,对角线AC、BD交于O,以B为圆心、BC长为半径画弧,交AB于点F,若点O恰好在圆弧上,且AB=6,则阴影部分的面积为( )
A.18﹣6π B.54﹣18π C.36﹣6π D.27﹣9π
14.中国美食讲究色香味美,优雅的摆盘造型也会让美食锦上添花.图①中的摆盘,其形状是扇形的一部分,图②是其几何示意图(阴影部分为摆盘),通过测量得到AC=BD=12cm,C,D两点之间的距离为4cm,圆心角为60°,则图中摆盘的面积是( )
A.80πcm2 B.40πcm2 C.24πcm2 D.2πcm2
15.如图,⊙A,⊙B,⊙C的半径都是2cm,则图中三个扇形(即阴影部分)面积之和是( )
A.2π B.π C. D.6π
16.如图,在扇形OAB中,已知∠AOB=90°,OA=,过的中点C作CD⊥OA,CE⊥OB,垂足分别为D、E,则图中阴影部分的面积为( )
A.π﹣1 B.﹣1 C.π﹣ D.﹣
17.如图,在△ABC中,∠C=90°,∠BAC=60°,AC=2,将△ABC绕点A顺时针旋转45°,得到△AB'C',B'C'与AB相交于点D,则图中阴影部分的面积为 .
18.如图,平行四边形ABCD中,∠A=60°,CD=4,以点A为圆心,AB的长为半径画弧交AD边于点E,以点B为圆心,BE的长为半径画弧交BC边于点F,则阴影部分的面积为 .
19.如图,AB是⊙O的弦,直线BC与⊙O相切于点B,AD⊥BC,垂足为D,连接OA,OB.
(1)求证:AB平分∠OAD;
(2)当∠AOB=100°,⊙O的半径为6cm时.
①直接写出扇形AOB的面积约为 cm2(结果精确到1cm2);
②点E是⊙O上一动点(点E不与点A、点B重合),连接AE,BE,请直接写出∠AEB= °.
20.如图,半圆O的直径AB=20,将半圆O绕点B顺时针旋转45°得到半圆O′,与AB交于点P.
(1)求AP的长;
(2)求图中阴影部分的面积(结果保留π).
参考答案
一.弧长的计算
1.解:∵、的长度分别为7π,11π,
∴圆的周长为18π,
∵∠A=80°,
∴∠C=180°﹣80°=100°,
故=×18π=10π.
故选:C.
2.解:A,1的倒数是,所以1的倒数是是错误的.
B,因为弧长公式:I=,所以计算弧长的公式是是错误的.
C,因为最小的自然数是0,所以所以1是最小的自然数,说法错误.
D,一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身.1的因数只有1.说法正确.
故选:D.
3.解:设第n秒运动到Pn(n为自然数)点,
观察,发现规律:P1(,),P2(1,0),P3(,﹣),P4(2,0),P5(,),…,
∴P4n+1(,),P4n+2(n+1,0),P4n+3(,﹣),P4n+4(2n+2,0).
∵2019=4×504+3,
∴P2019为(,﹣),
故选:B.
4.解:连接OB,OC.
∵∠BOC=2∠BAC=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴OB=OC=BC=1,
∴劣弧的长==,
故选:B.
5.解:∵扇形的弧长为,半径为2,
∴=,
解得:n=45°.
故选:B.
6.解:设这条弧所在圆的半径为R,
由题意得,=5π,
解得,R=6,
故答案为:6.
7.解:连接OB,
∵AB=,CD是⊙O的直径,
∴BE=AB=,
∵OB=CD=1,
∴sin∠DOB==,
∴∠DOB=60°,
∴∠BOC=120°,
∴的长为=π,
故答案为:π.
8.解:由图可知,
阴影部分的周长是:(3﹣2)+(3﹣2)=+2=(+2)cm,
故答案为:(+2).
9.解:(1)∵AB是⊙O的直径,
∴∠ADB=90°.
∵同弧所对的圆周角相等,
∴∠ABD=∠ACD=30°.
∵AD=4,
∴AB=8.
∴⊙O的直径为8cm.
(2)连接OD,则∠AOD=2∠ACD=60°.
∴的长为.
10.解:(1)如图,过P作PA⊥x轴于A,
∵P(1,3),
∴,
∴点P经过的弧长为;
(2)把点P绕坐标原点O逆时针旋转90°后得到点Q,过点P作x轴的垂线,垂足是B,
∴OQ=PO,∠POQ=90°,
∴∠POA+∠QOB=90°,∠QOB=∠OPA,△QOB≌△OPA(AAS),
∴OB=PA=3,BQ=AO=1,
则点Q的坐标是(﹣3,1).
故答案是:(﹣3,1).
11.解:(1)∵的半径OA=2,OC⊥AB于点C,∠AOC=60°,
∴AC=OA sin60°=2×=,
∴AB=2AC=2;
(2)∵OC⊥AB,∠AOC=60°,
∴∠AOB=120°,
∵OA=2,
∴的长是:=.
二.扇形面积的计算
12.解:∵点A的坐标是(3,4),点B的坐标是(﹣4,3),
∴∠AOB=90°,OA=OB==5,
∴扇形OAB的面积==π,
故选:D.
13.解:∵四边形ABCD是矩形,
∴AB=CD=6,∠DCB=90°,AC=BD,OC=AC,OB=BD,
∴OB=OC,
∵BC=OB,
∴△OBC是等边三角形,
∴∠CBO=60°,BC=BO,
即AC=2BC,
在Rt△ABC中,由勾股定理得:AB2+BC2=AC2,
(6)2+BC2=(2BC)2,
解得:BC=6,
∴阴影部分的面积=S△BCD﹣S扇形BOC=﹣=18﹣6π,
故选:A.
14.解:如图,连接CD.
∵OC=OD,∠O=60°,
∴△COD是等边三角形,
∴OC=OD=CD=4cm,
∴S阴=S扇形OAB﹣S扇形OCD=﹣=40π(cm2),
故选:B.
15.解:∵∠A+∠B+∠C=180°,
∴阴影部分的面积==2π.
故选:A.
16.解:∵CD⊥OA,CE⊥OB,
∴∠CDO=∠CEO=∠AOB=90°,
∴四边形CDOE是矩形,
连接OC,
∵点C是的中点,
∴∠AOC=∠BOC,
∵OC=OC,
∴△COD≌△COE(AAS),
∴OD=OE,
∴矩形CDOE是正方形,
∵OC=OA=,
∴OE=1,
∴图中阴影部分的面积=﹣1×1=﹣1,
故选:B.
17.解:∵在△ABC中,∠C=90°,∠BAC=60°,AC=2,
∴AB=2AC=4,∠ABC=30°,
过D作DH⊥AB′于H,
∵将△ABC绕点A顺时针旋转45°,得到△AB'C',
∴AB′=AB=4,∠AB′C′=∠ABC=30°,∠BAB′=45°,AC′=AC=2,
设DH=AH=x,
∴B′H=DH=x,
∴AH+B′H=x+x=AB′=4,
∴x=2(﹣1),
∴B′D=2DH=4(﹣1),
∴图中阴影部分的面积=S扇形BAB′﹣S△ADB′=﹣=2π﹣4(﹣1),
故答案为:2π﹣4(﹣1).
18.解:如图连接BE,EF.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠ABC=180°,
∵∠A=60°,
∴∠ABC=120°,
∵AE=AB,
∴△ABE是等边三角形,
∴∠ABE=∠EBF=60°,
∵BE=BF,
∴△EBF是等边三角形,
∵S阴=S△BEF=×42=4,
故答案为4.
19.(1)证明:∵OA=OB,
∴∠OBA=∠OAB,
∵OB⊥CB,AD⊥BC,
∴OB∥AD,
∴∠OBA=∠DAB,
∴∠OAB=∠DAB,
∴AB平分∠OAD;
(2)①∵∠AOB=100°,⊙O的半径为6cm,
∴扇形AOB的面积为:≈31(cm2),
故答案为:31;
②当点E在优弧AB上时,
∵∠AOB=100°,
∴∠AEB=50°,
当点E在劣弧AB上时,
∠AEB=180°﹣50°=130°,
故答案为:50或130.
20.解:(1)∵∠OBA′=45°,O′P=O′B,
∴△O′PB是等腰直角三角形,
∴PB=BO,
∴AP=AB﹣BP=20﹣10;
(2)阴影部分面积为:
S阴影=S扇形O′A′P+S△O′PB=×π×100+10×10×=25π+50.
