24.2 点和圆、直线和圆位置关系 测试卷 2021-2022学年人教版数学九年级上册(word版 含答案)
文档属性
| 名称 | 24.2 点和圆、直线和圆位置关系 测试卷 2021-2022学年人教版数学九年级上册(word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 712.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 19:41:17 | ||
图片预览


文档简介
初中数学九年级上册第二十四章点和圆、直线和圆
位置关系测试卷
一、单选题
1.有下列说法:①直径是圆中最长的弦;②圆的两条平行弦所夹的弧相等;③任意一个三角形有且只有一个外接圆;④平分弦的直径垂直于弦.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
2.已知的半径为,点P在上,则的长是( )
A. B. C. D.
3.⊙O的半径为5,点P到圆心O的距离为5,点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O外 C.点P在⊙O上 D.无法确定
4.下列说法正确的是( )
A.等弧所对的圆心角相等 B.同弦所对的圆周角相等
C.经过三点可以作一个圆 D.相等的圆心角所对的弧相等
5.如图,点E为Rt△ABC的直角边AC上一点,以CE为直径的半圆与斜边AB相切于点D,连结DE.若∠B=70°,则∠CED为( )
A.70° B.65° C.55° D.35°
6.如图,是外一点,、切于点、,点在优弧上,若,则等于( )
A. B. C. D.
7.在中,,,,若以点为圆心,为半径的与直线相切,则的值为( )
A.2.4 B.3 C.4.8 D.5
8.如图,在△ABC中,AB=AC,∠B=30°,以点A为圆心,以3cm为半径作⊙A.若BC与⊙A相切,则AB的长为( )cm.
A.3 B.3 C.6 D.2
9.的半径为6cm,圆心到直线的距离为7cm,则直线与的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
二、填空题
10.如图AB、AC、BD是圆O的切线,切点分别为P、C、D,若AB=5,BD=2,则AC的长是 __.
11.圆的切线垂直于经过切点的_________.
推论1:经过圆心且垂直于切线的直线必经过____________.
推论2:经过切点且垂直于切线的直线必经过__________.
12.如图,∠ACB=60°,半径为2的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离为_______.
13.如图,在⊙O中,AB是直径,CD是⊙O的切线,直线AB和ED交于点C,∠ADE=60°,则∠C的度数为__________.
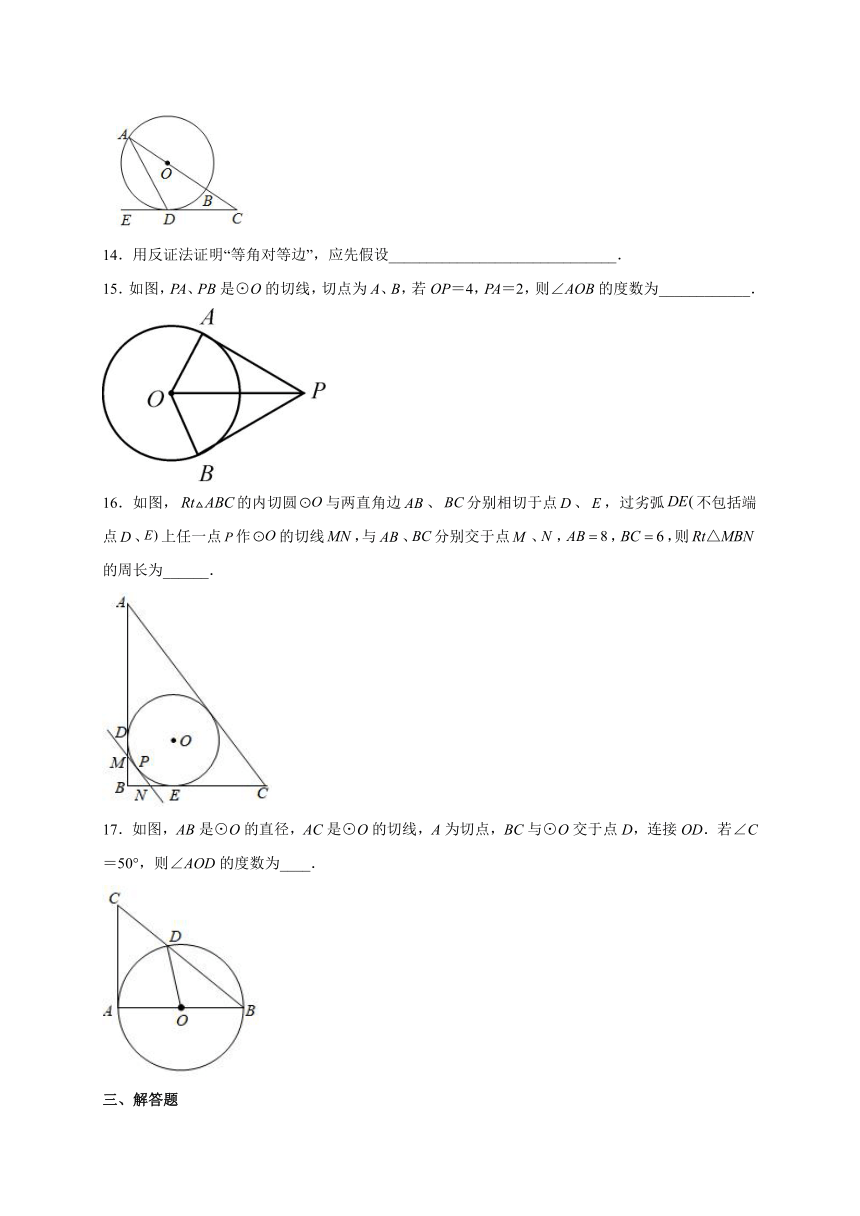
14.用反证法证明“等角对等边”,应先假设______________________________.
15.如图,PA、PB是⊙O的切线,切点为A、B,若OP=4,PA=2,则∠AOB的度数为____________.
16.如图,的内切圆与两直角边、分别相切于点、,过劣弧不包括端点、上任一点作的切线,与、分别交于点、,,,则的周长为______.
17.如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,BC与⊙O交于点D,连接OD.若∠C=50°,则∠AOD的度数为____.
三、解答题
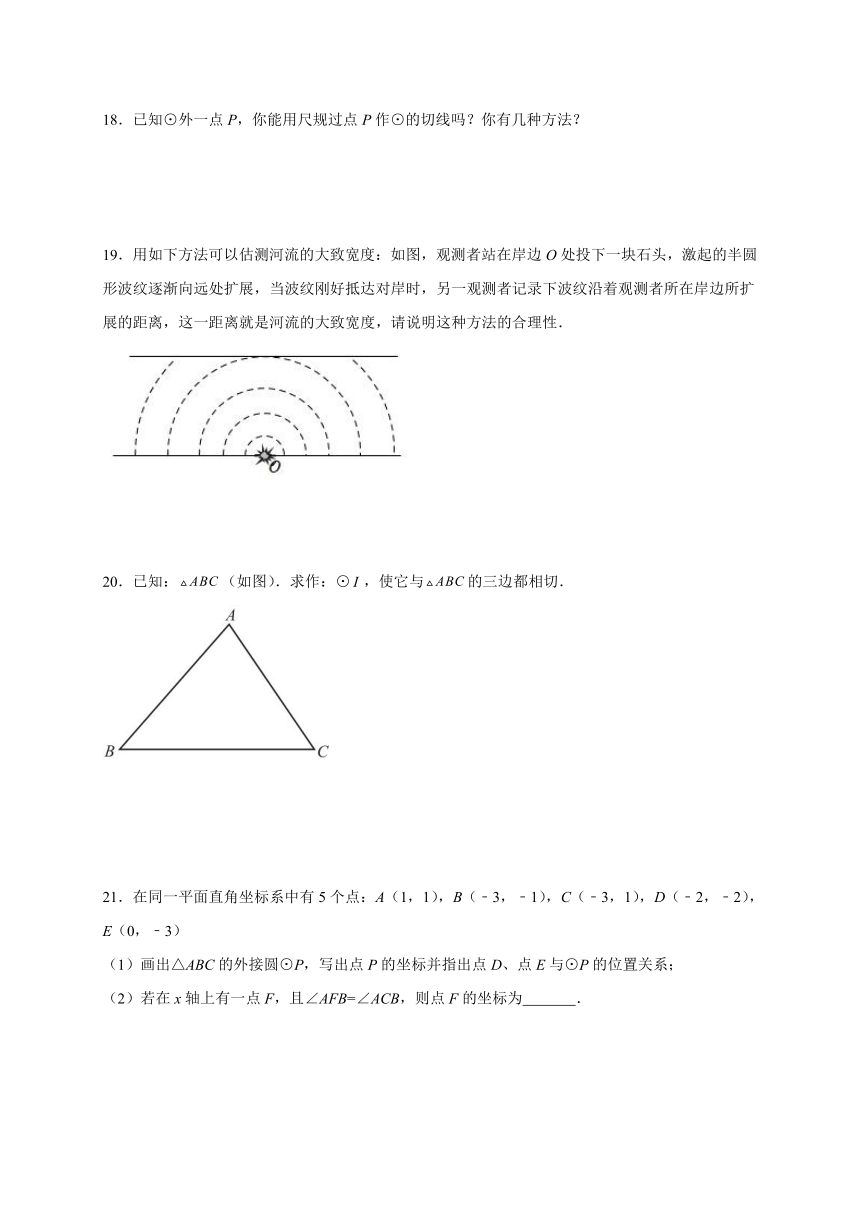
18.已知⊙外一点P,你能用尺规过点P作⊙的切线吗?你有几种方法?
19.用如下方法可以估测河流的大致宽度:如图,观测者站在岸边O处投下一块石头,激起的半圆形波纹逐渐向远处扩展,当波纹刚好抵达对岸时,另一观测者记录下波纹沿着观测者所在岸边所扩展的距离,这一距离就是河流的大致宽度,请说明这种方法的合理性.
20.已知:(如图).求作:⊙,使它与的三边都相切.
21.在同一平面直角坐标系中有5个点:A(1,1),B(﹣3,﹣1),C(﹣3,1),D(﹣2,﹣2),E(0,﹣3)
(1)画出△ABC的外接圆⊙P,写出点P的坐标并指出点D、点E与⊙P的位置关系;
(2)若在x轴上有一点F,且∠AFB=∠ACB,则点F的坐标为 .
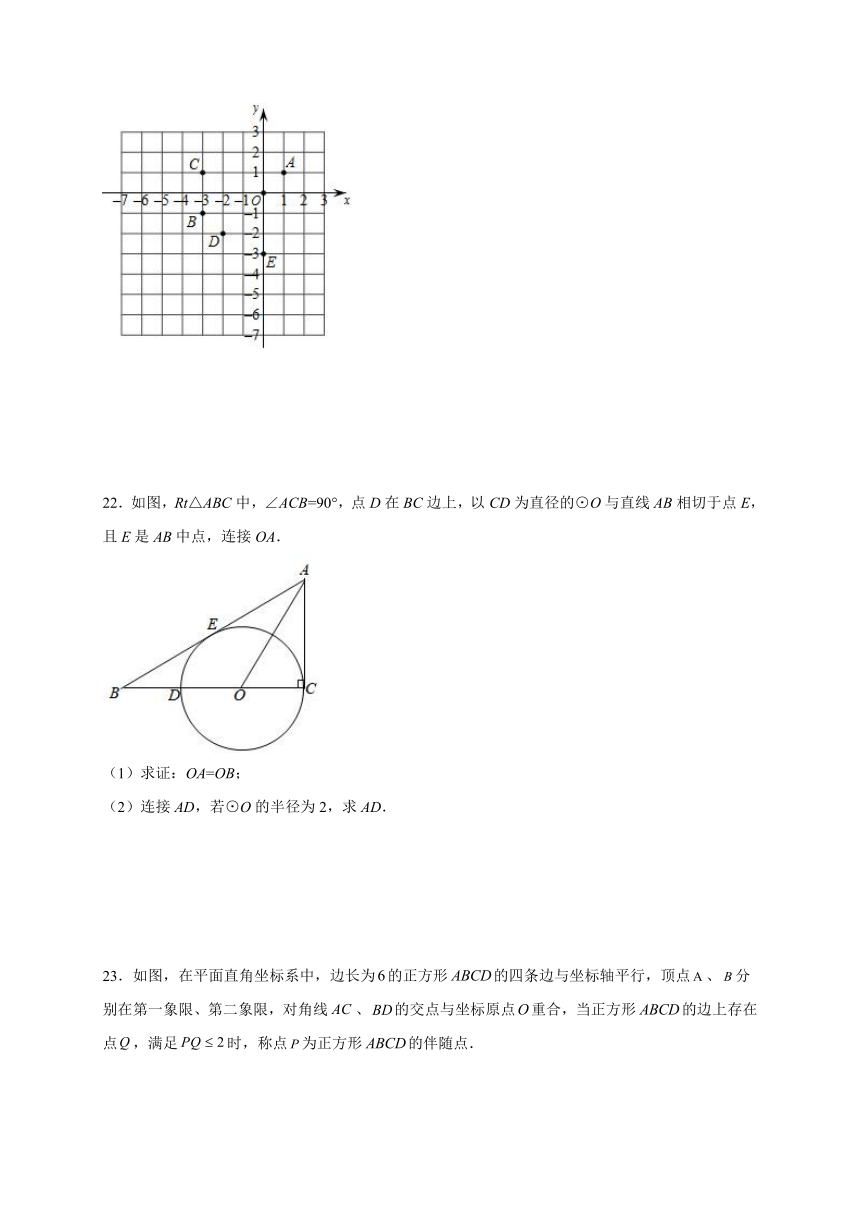
22.如图,Rt△ABC中,∠ACB=90°,点D在BC边上,以CD为直径的⊙O与直线AB相切于点E,且E是AB中点,连接OA.
(1)求证:OA=OB;
(2)连接AD,若⊙O的半径为2,求AD.
23.如图,在平面直角坐标系中,边长为的正方形的四条边与坐标轴平行,顶点、分别在第一象限、第二象限,对角线、的交点与坐标原点重合,当正方形的边上存在点,满足时,称点为正方形的伴随点.
(1)点的坐标为点______,的坐标为______,点的坐标为______,点的坐标为______.
(2)当正方形的伴随点的坐标为时,点的坐标可以为______(写出一个即可).
(3)在点、、、中,正方形的伴随点是______.
(4)点在直线上.若点为正方形的伴随点,直接写出点横坐标的取值范围.
试卷第1页,共3页
参考答案
1.C
【详解】
解:①直径是圆中最长的弦;故①正确,符合题意;
②圆的两条平行弦所夹的弧相等;故②正确,符合题意;
③任意一个三角形有且只有一个外接圆;故③正确,符合题意;
④平分弦(非直径)的直径垂直于弦;故④错误,不符合题意;
其中正确的有3个,
2.C
【详解】
解:∵点P在上,
∴的长等于圆的半径,即 .
故选:C
3.C
【详解】
解:∵⊙O的半径为5,点P到圆心O的距离为5,
∴点P到圆心O的距离等于圆的半径,
∴点P在⊙O上.
4.A
【详解】
解:等弧所对的圆心角相等,故A正确;
在同圆或等圆中,同弦所对的圆周角相等或互补,故B错误;
经过不在同一直线上的三点可以作一个圆,故C错误;
在同圆或等圆中,相等的圆心角所对的弧相等,故D错误,
5.C
【详解】
解:连接,
∵,
∴与半圆相切与点,
∵半圆与斜边AB相切于点D,
∴,
∵∠B=70°,
∴,
∴,
∵CE为直径,
∴,
∴∠CED,
6.C
【详解】
解:、都为圆的切线,
,
,
,
与都对,
.
7.C
【详解】
解:如图所示,过C作CD⊥AB,交AB于点D,
在Rt△ABC中,AC=6cm,BC=8cm,
根据勾股定理得:AB==10(cm),
∵S△ABC=BC AC=AB CD,
∴×6×8=×10×CD,
解得:CD=4.8,
则r=4.8(cm).
8.C
【详解】
解:设BC与⊙A的切点为D,连接AD,
则AD⊥BC,
在Rt△ABD中,∠B=30°,
∴AB=2AD=6(cm),
9.C
【详解】
解:的半径为,圆心到直线的距离为,,
直线与相离.
10.3
【详解】
解:∵AC、AP为⊙O的切线,
∴AC=AP,
∵BP、BD为⊙O的切线,
∴BP=BD,
∴AC=AP=AB-BP=5-2=3.
故答案为:3.
11.半径 切点 圆心
12.
【详解】
解:如图,设⊙O滚动到如图位置时,与AC相切于点E,与BC相切与点F,连接OC,OE,OF,
∵⊙O与AC和BC都相切,E和F为切点,
∴OF⊥BC,OE⊥AC,
∵∠ACB=60°,OF=OE,
∴∠BCO=30°,
∵OF=2,
∴OC=4,
∴由勾股定理得,OF2+CF2=CO2,
∴.
∴圆心O水平移动的距离为,
故答案为:.
13.30°
【详解】
解:如图所示,连接OD,
∵EC是圆O的切线,
∴∠ODE=∠ODC=90°,
∵∠ADE=60°,
∴∠ADO=30°,∠ADC=120°
∵OA=OD,
∴∠OAD=∠ODA=30°,
∴∠C=180°-∠DAC-∠ADC=30°,
故答案为:30°.
14.一个三角形中有两个角相等,那么这两个角所对的边不相等
【详解】
解:用反证法证明“等角对等边”,应先假设一个三角形中有两个角相等,那么这两个角所对的边不相等,
故答案为:一个三角形中有两个角相等,那么这两个角所对的边不相等.
15.120°
16.
【详解】
解:如图,连接、,
在中,,
设内切圆半径为,
、为的切线,
,,
又,,
四边形为正方形,
,
由切线长定理得:,,,,
,
解得,
则的周长为,
,
,
,
,
,
,
故答案为:.
17.
【详解】
解:∵是的直径,是的切线,
∴,
∴,
∵,
∴,
∵OB=OD,
∴,
∴,
故答案为:.
18.能,见解析
【详解】
如图,连接,以为直径作,与相交于A,B两点,则,即为的切线.
19.见解析
【详解】
解:这种方法是合理的,
理由如下:由题意得,半圆与观测者所在岸边所在的直线相切,
与观测者所在岸边垂直,
是点到观测者所在岸边的距离,
另一方面,为的半径,
∴,
∴只要测出就可以知道的长度了,
∴这种方法是合理的.
20.见解析
【详解】
解:如下图所示:分别作,的平分线和,交点为I,再过I作BC的垂线,垂足为D,再以I为圆心,以ID的长为半径作⊙.
21.(1)图见解析,P(-1,0),点D在圆上,点E在圆外;(2)或
【详解】
解:(1)∵A(1,1),B(﹣3,﹣1),C(﹣3,1),
∴AB=,AC=4,BC=2,
∵AC2+BC2=16+4=20=AB2,
∴△ABC为直角三角形,
以AB中点P(-1,0)为圆心,以AP=为半径画圆,
如图所示:
∵D(﹣2,﹣2),E(0,﹣3),
∴DP=,
∴点D在⊙P上;
∴EP=>,
∴点E在⊙P外,
(2)∵∠ACB=90°,AB为直径,
∴⊙P与x轴的交点为F,
设点F(m,0).
∴FB2+FA2=AB2,AF=,BF=,
∴,
整理得,
解得,
点F坐标为或.
故答案为或.
22.(1)见解析;(2).
【详解】
(1)证明:连接OE,如图:
以CD为直径的⊙O与直线AB相切于点E,
E是AB中点,
OE垂直平分AB
(2)
AO平分
由(1)知,OA=OB
在中,.
23.(1),,,;(2)答案不唯一;(3)、;(4)或
【详解】
解:(1)已知正方形边长为,
且正方形的四条边与坐标轴平行,对角线、的交点与坐标原点重合,
∴,,,;
故答案为:,,,;
(2)已知点在正方形的边上,且,
又∵,
∴点(答案不唯一),
故答案为:(答案不唯一);
(3)①如图以点为圆心,为半径作圆,与正方形无交点,
∴不是正方形的伴随点;
②如图以点为圆心,为半径作圆,与正方形无交点,
∴不是正方形的伴随点;
③如图以点为圆心,为半径作圆,与正方形有交点,
∴是正方形的伴随点;
④如图以点为圆心,为半径作圆,与正方形有交点,
∴是正方形的伴随点;
故答案为:,;
(4)如图符合条件的临界点有4个,如图,过点作轴于,过点作轴于,
∵点,点在上,
∴,
∵正方形边长为6,
∴,
∴,,
∴,,
∴,
∴, ,
∴,
同理可得,,
∴,
综上,或.
答案第1页,共2页
答案第1页,共2页
位置关系测试卷
一、单选题
1.有下列说法:①直径是圆中最长的弦;②圆的两条平行弦所夹的弧相等;③任意一个三角形有且只有一个外接圆;④平分弦的直径垂直于弦.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
2.已知的半径为,点P在上,则的长是( )
A. B. C. D.
3.⊙O的半径为5,点P到圆心O的距离为5,点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O外 C.点P在⊙O上 D.无法确定
4.下列说法正确的是( )
A.等弧所对的圆心角相等 B.同弦所对的圆周角相等
C.经过三点可以作一个圆 D.相等的圆心角所对的弧相等
5.如图,点E为Rt△ABC的直角边AC上一点,以CE为直径的半圆与斜边AB相切于点D,连结DE.若∠B=70°,则∠CED为( )
A.70° B.65° C.55° D.35°
6.如图,是外一点,、切于点、,点在优弧上,若,则等于( )
A. B. C. D.
7.在中,,,,若以点为圆心,为半径的与直线相切,则的值为( )
A.2.4 B.3 C.4.8 D.5
8.如图,在△ABC中,AB=AC,∠B=30°,以点A为圆心,以3cm为半径作⊙A.若BC与⊙A相切,则AB的长为( )cm.
A.3 B.3 C.6 D.2
9.的半径为6cm,圆心到直线的距离为7cm,则直线与的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
二、填空题
10.如图AB、AC、BD是圆O的切线,切点分别为P、C、D,若AB=5,BD=2,则AC的长是 __.
11.圆的切线垂直于经过切点的_________.
推论1:经过圆心且垂直于切线的直线必经过____________.
推论2:经过切点且垂直于切线的直线必经过__________.
12.如图,∠ACB=60°,半径为2的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离为_______.
13.如图,在⊙O中,AB是直径,CD是⊙O的切线,直线AB和ED交于点C,∠ADE=60°,则∠C的度数为__________.
14.用反证法证明“等角对等边”,应先假设______________________________.
15.如图,PA、PB是⊙O的切线,切点为A、B,若OP=4,PA=2,则∠AOB的度数为____________.
16.如图,的内切圆与两直角边、分别相切于点、,过劣弧不包括端点、上任一点作的切线,与、分别交于点、,,,则的周长为______.
17.如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,BC与⊙O交于点D,连接OD.若∠C=50°,则∠AOD的度数为____.
三、解答题
18.已知⊙外一点P,你能用尺规过点P作⊙的切线吗?你有几种方法?
19.用如下方法可以估测河流的大致宽度:如图,观测者站在岸边O处投下一块石头,激起的半圆形波纹逐渐向远处扩展,当波纹刚好抵达对岸时,另一观测者记录下波纹沿着观测者所在岸边所扩展的距离,这一距离就是河流的大致宽度,请说明这种方法的合理性.
20.已知:(如图).求作:⊙,使它与的三边都相切.
21.在同一平面直角坐标系中有5个点:A(1,1),B(﹣3,﹣1),C(﹣3,1),D(﹣2,﹣2),E(0,﹣3)
(1)画出△ABC的外接圆⊙P,写出点P的坐标并指出点D、点E与⊙P的位置关系;
(2)若在x轴上有一点F,且∠AFB=∠ACB,则点F的坐标为 .
22.如图,Rt△ABC中,∠ACB=90°,点D在BC边上,以CD为直径的⊙O与直线AB相切于点E,且E是AB中点,连接OA.
(1)求证:OA=OB;
(2)连接AD,若⊙O的半径为2,求AD.
23.如图,在平面直角坐标系中,边长为的正方形的四条边与坐标轴平行,顶点、分别在第一象限、第二象限,对角线、的交点与坐标原点重合,当正方形的边上存在点,满足时,称点为正方形的伴随点.
(1)点的坐标为点______,的坐标为______,点的坐标为______,点的坐标为______.
(2)当正方形的伴随点的坐标为时,点的坐标可以为______(写出一个即可).
(3)在点、、、中,正方形的伴随点是______.
(4)点在直线上.若点为正方形的伴随点,直接写出点横坐标的取值范围.
试卷第1页,共3页
参考答案
1.C
【详解】
解:①直径是圆中最长的弦;故①正确,符合题意;
②圆的两条平行弦所夹的弧相等;故②正确,符合题意;
③任意一个三角形有且只有一个外接圆;故③正确,符合题意;
④平分弦(非直径)的直径垂直于弦;故④错误,不符合题意;
其中正确的有3个,
2.C
【详解】
解:∵点P在上,
∴的长等于圆的半径,即 .
故选:C
3.C
【详解】
解:∵⊙O的半径为5,点P到圆心O的距离为5,
∴点P到圆心O的距离等于圆的半径,
∴点P在⊙O上.
4.A
【详解】
解:等弧所对的圆心角相等,故A正确;
在同圆或等圆中,同弦所对的圆周角相等或互补,故B错误;
经过不在同一直线上的三点可以作一个圆,故C错误;
在同圆或等圆中,相等的圆心角所对的弧相等,故D错误,
5.C
【详解】
解:连接,
∵,
∴与半圆相切与点,
∵半圆与斜边AB相切于点D,
∴,
∵∠B=70°,
∴,
∴,
∵CE为直径,
∴,
∴∠CED,
6.C
【详解】
解:、都为圆的切线,
,
,
,
与都对,
.
7.C
【详解】
解:如图所示,过C作CD⊥AB,交AB于点D,
在Rt△ABC中,AC=6cm,BC=8cm,
根据勾股定理得:AB==10(cm),
∵S△ABC=BC AC=AB CD,
∴×6×8=×10×CD,
解得:CD=4.8,
则r=4.8(cm).
8.C
【详解】
解:设BC与⊙A的切点为D,连接AD,
则AD⊥BC,
在Rt△ABD中,∠B=30°,
∴AB=2AD=6(cm),
9.C
【详解】
解:的半径为,圆心到直线的距离为,,
直线与相离.
10.3
【详解】
解:∵AC、AP为⊙O的切线,
∴AC=AP,
∵BP、BD为⊙O的切线,
∴BP=BD,
∴AC=AP=AB-BP=5-2=3.
故答案为:3.
11.半径 切点 圆心
12.
【详解】
解:如图,设⊙O滚动到如图位置时,与AC相切于点E,与BC相切与点F,连接OC,OE,OF,
∵⊙O与AC和BC都相切,E和F为切点,
∴OF⊥BC,OE⊥AC,
∵∠ACB=60°,OF=OE,
∴∠BCO=30°,
∵OF=2,
∴OC=4,
∴由勾股定理得,OF2+CF2=CO2,
∴.
∴圆心O水平移动的距离为,
故答案为:.
13.30°
【详解】
解:如图所示,连接OD,
∵EC是圆O的切线,
∴∠ODE=∠ODC=90°,
∵∠ADE=60°,
∴∠ADO=30°,∠ADC=120°
∵OA=OD,
∴∠OAD=∠ODA=30°,
∴∠C=180°-∠DAC-∠ADC=30°,
故答案为:30°.
14.一个三角形中有两个角相等,那么这两个角所对的边不相等
【详解】
解:用反证法证明“等角对等边”,应先假设一个三角形中有两个角相等,那么这两个角所对的边不相等,
故答案为:一个三角形中有两个角相等,那么这两个角所对的边不相等.
15.120°
16.
【详解】
解:如图,连接、,
在中,,
设内切圆半径为,
、为的切线,
,,
又,,
四边形为正方形,
,
由切线长定理得:,,,,
,
解得,
则的周长为,
,
,
,
,
,
,
故答案为:.
17.
【详解】
解:∵是的直径,是的切线,
∴,
∴,
∵,
∴,
∵OB=OD,
∴,
∴,
故答案为:.
18.能,见解析
【详解】
如图,连接,以为直径作,与相交于A,B两点,则,即为的切线.
19.见解析
【详解】
解:这种方法是合理的,
理由如下:由题意得,半圆与观测者所在岸边所在的直线相切,
与观测者所在岸边垂直,
是点到观测者所在岸边的距离,
另一方面,为的半径,
∴,
∴只要测出就可以知道的长度了,
∴这种方法是合理的.
20.见解析
【详解】
解:如下图所示:分别作,的平分线和,交点为I,再过I作BC的垂线,垂足为D,再以I为圆心,以ID的长为半径作⊙.
21.(1)图见解析,P(-1,0),点D在圆上,点E在圆外;(2)或
【详解】
解:(1)∵A(1,1),B(﹣3,﹣1),C(﹣3,1),
∴AB=,AC=4,BC=2,
∵AC2+BC2=16+4=20=AB2,
∴△ABC为直角三角形,
以AB中点P(-1,0)为圆心,以AP=为半径画圆,
如图所示:
∵D(﹣2,﹣2),E(0,﹣3),
∴DP=,
∴点D在⊙P上;
∴EP=>,
∴点E在⊙P外,
(2)∵∠ACB=90°,AB为直径,
∴⊙P与x轴的交点为F,
设点F(m,0).
∴FB2+FA2=AB2,AF=,BF=,
∴,
整理得,
解得,
点F坐标为或.
故答案为或.
22.(1)见解析;(2).
【详解】
(1)证明:连接OE,如图:
以CD为直径的⊙O与直线AB相切于点E,
E是AB中点,
OE垂直平分AB
(2)
AO平分
由(1)知,OA=OB
在中,.
23.(1),,,;(2)答案不唯一;(3)、;(4)或
【详解】
解:(1)已知正方形边长为,
且正方形的四条边与坐标轴平行,对角线、的交点与坐标原点重合,
∴,,,;
故答案为:,,,;
(2)已知点在正方形的边上,且,
又∵,
∴点(答案不唯一),
故答案为:(答案不唯一);
(3)①如图以点为圆心,为半径作圆,与正方形无交点,
∴不是正方形的伴随点;
②如图以点为圆心,为半径作圆,与正方形无交点,
∴不是正方形的伴随点;
③如图以点为圆心,为半径作圆,与正方形有交点,
∴是正方形的伴随点;
④如图以点为圆心,为半径作圆,与正方形有交点,
∴是正方形的伴随点;
故答案为:,;
(4)如图符合条件的临界点有4个,如图,过点作轴于,过点作轴于,
∵点,点在上,
∴,
∵正方形边长为6,
∴,
∴,,
∴,,
∴,
∴, ,
∴,
同理可得,,
∴,
综上,或.
答案第1页,共2页
答案第1页,共2页
同课章节目录
