2021-2022学年人教版数学九年级上册24.4 弧长和扇形面积 测试卷(word版、含解析)
文档属性
| 名称 | 2021-2022学年人教版数学九年级上册24.4 弧长和扇形面积 测试卷(word版、含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1024.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 00:00:00 | ||
图片预览

文档简介
初中数学九年级上册第二十四章弧长和扇形面积测试卷
一、单选题
1.如图,四边形的顶点,,都在上,,,,则的弧长为( )
A. B. C. D.
2.如图,在中,,,斜边是半圆的直径,点是半圆上的一个动点,连接与交于点,若是等腰三角形,则弧的长为( )
A. B.或 C.或 D.或
3.如图,一张扇形纸片OAB,∠AOB=120°,OA=6,将这张扇形纸片折叠,使点A与点O重合,折痕为CD,则图中未重叠部分(即阴影部分)的面积为( )
A. B. C. D.
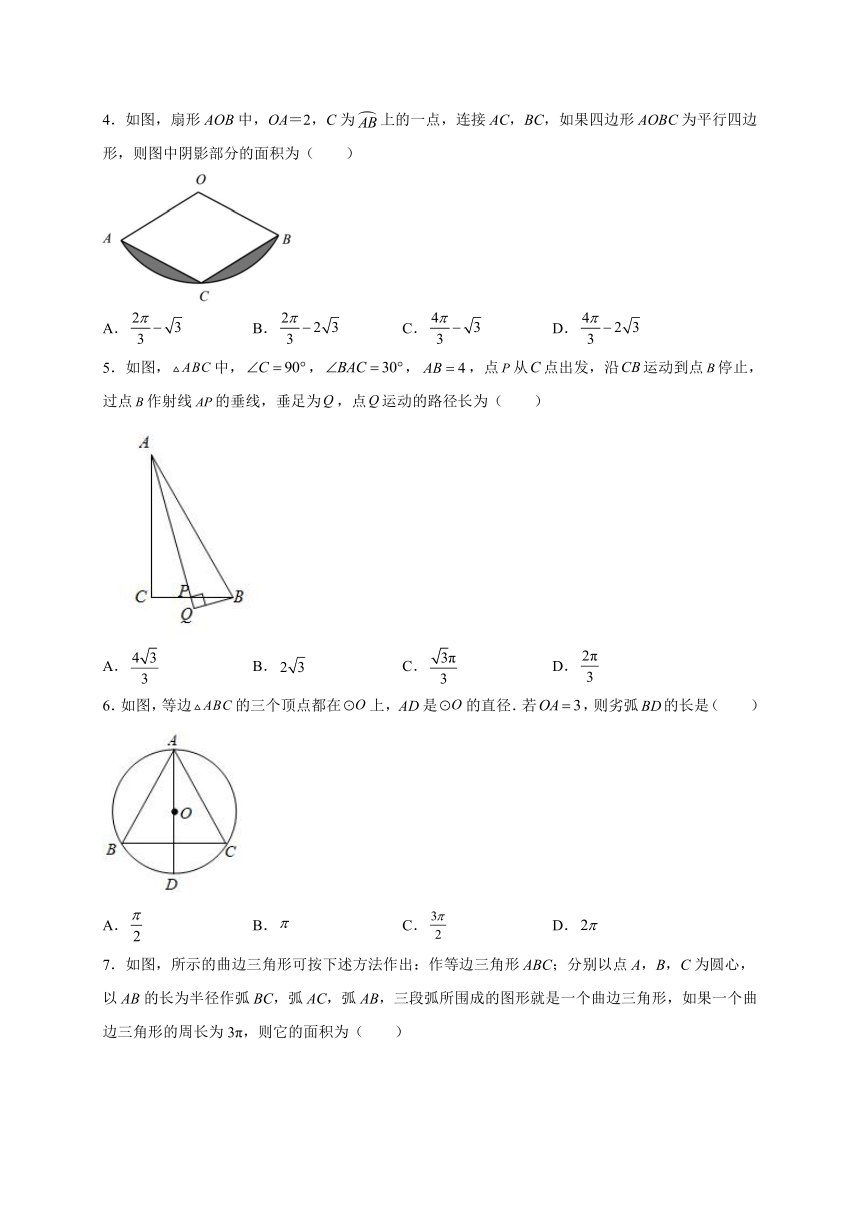
4.如图,扇形AOB中,OA=2,C为上的一点,连接AC,BC,如果四边形AOBC为平行四边形,则图中阴影部分的面积为( )
A. B. C. D.
5.如图,中,,,,点从点出发,沿运动到点停止,过点作射线的垂线,垂足为,点运动的路径长为( )
A. B. C. D.
6.如图,等边的三个顶点都在上,是的直径.若,则劣弧的长是( )
A. B. C. D.
7.如图,所示的曲边三角形可按下述方法作出:作等边三角形ABC;分别以点A,B,C为圆心,以AB的长为半径作弧BC,弧AC,弧AB,三段弧所围成的图形就是一个曲边三角形,如果一个曲边三角形的周长为3π,则它的面积为( )
A. B. C. D.
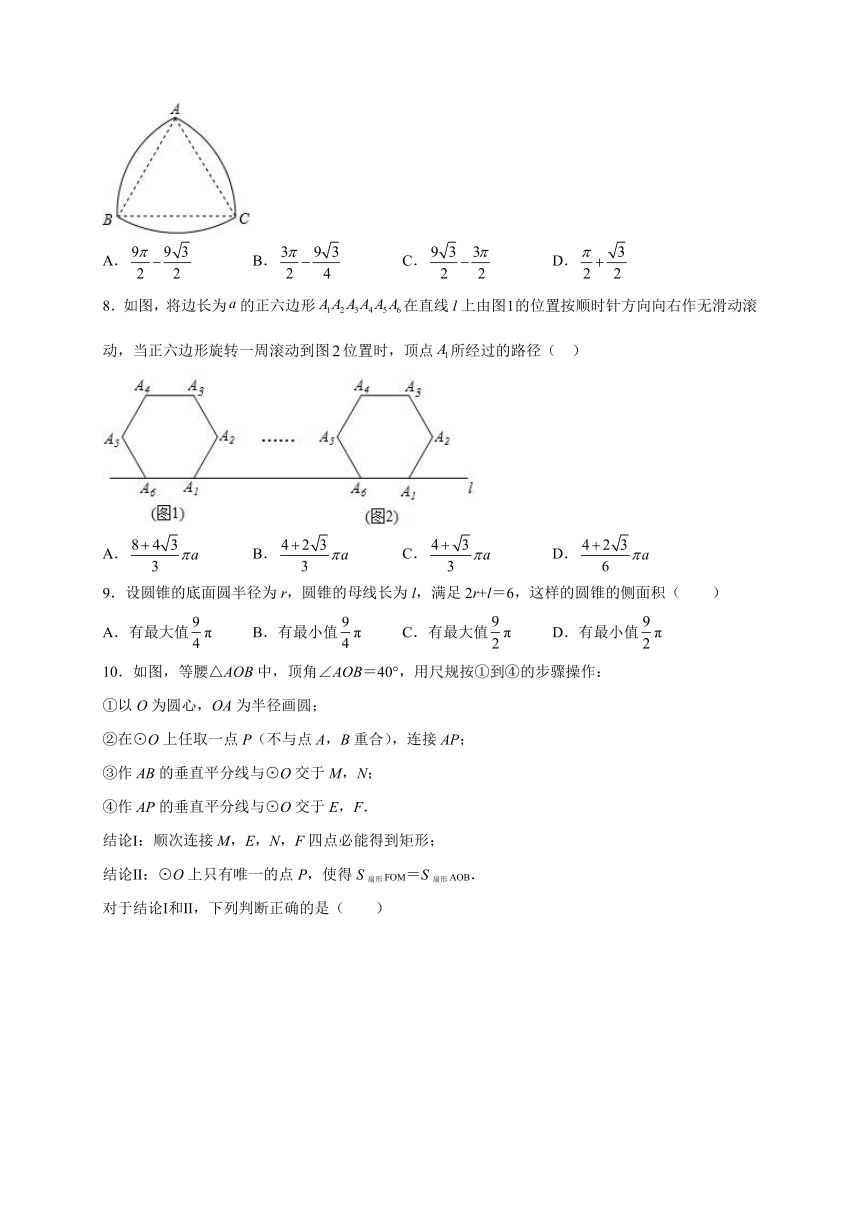
8.如图,将边长为的正六边形在直线l上由图的位置按顺时针方向向右作无滑动滚动,当正六边形旋转一周滚动到图位置时,顶点所经过的路径( )
A. B. C. D.
9.设圆锥的底面圆半径为r,圆锥的母线长为l,满足2r+l=6,这样的圆锥的侧面积( )
A.有最大值π B.有最小值π C.有最大值π D.有最小值π
10.如图,等腰△AOB中,顶角∠AOB=40°,用尺规按①到④的步骤操作:
①以O为圆心,OA为半径画圆;
②在⊙O上任取一点P(不与点A,B重合),连接AP;
③作AB的垂直平分线与⊙O交于M,N;
④作AP的垂直平分线与⊙O交于E,F.
结论Ⅰ:顺次连接M,E,N,F四点必能得到矩形;
结论Ⅱ:⊙O上只有唯一的点P,使得S扇形FOM=S扇形AOB.
对于结论Ⅰ和Ⅱ,下列判断正确的是( )
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对 C.Ⅰ不对Ⅱ对 D.Ⅰ对Ⅱ不对
二、填空题
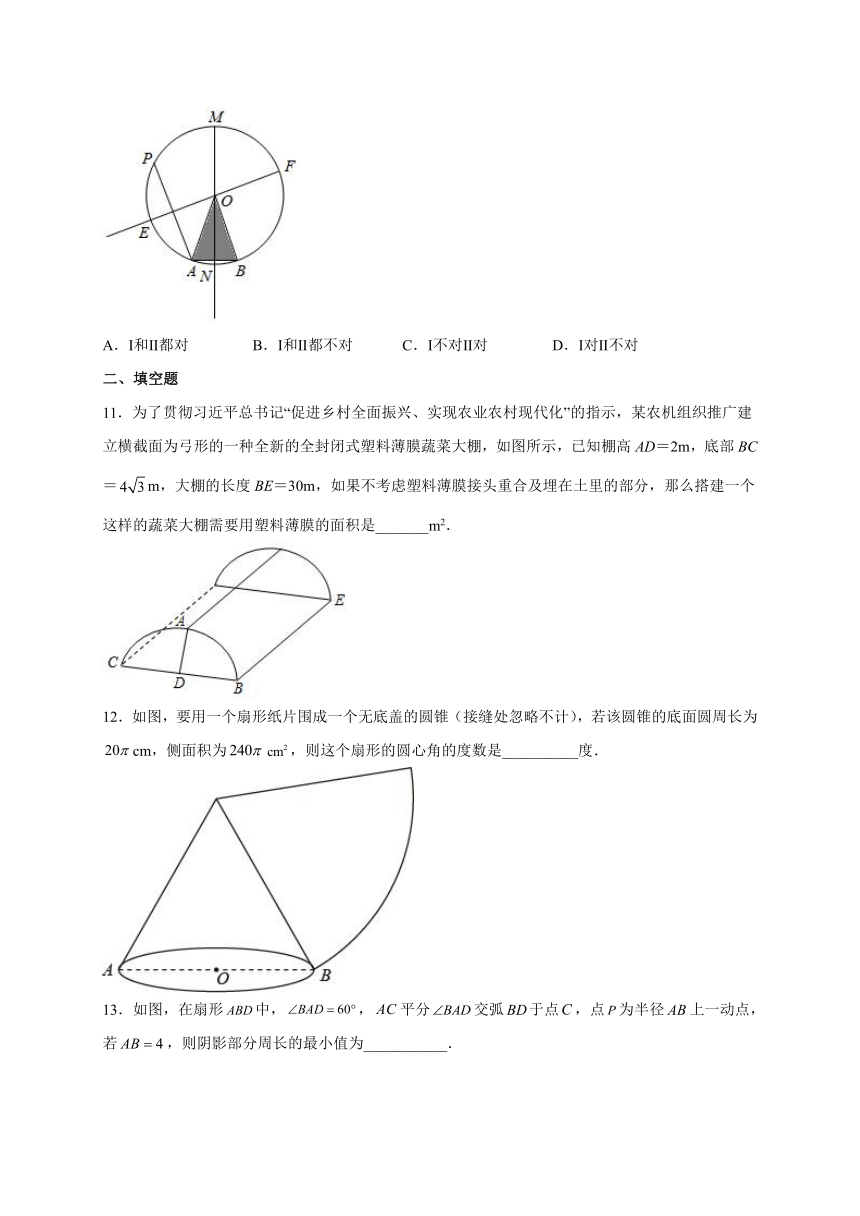
11.为了贯彻习近平总书记“促进乡村全面振兴、实现农业农村现代化”的指示,某农机组织推广建立横截面为弓形的一种全新的全封闭式塑料薄膜蔬菜大棚,如图所示,已知棚高AD=2m,底部BC=m,大棚的长度BE=30m,如果不考虑塑料薄膜接头重合及埋在土里的部分,那么搭建一个这样的蔬菜大棚需要用塑料薄膜的面积是_______m2.
12.如图,要用一个扇形纸片围成一个无底盖的圆锥(接缝处忽略不计),若该圆锥的底面圆周长为cm,侧面积为,则这个扇形的圆心角的度数是__________度.
13.如图,在扇形中,,平分交弧于点,点为半径上一动点,若,则阴影部分周长的最小值为___________.
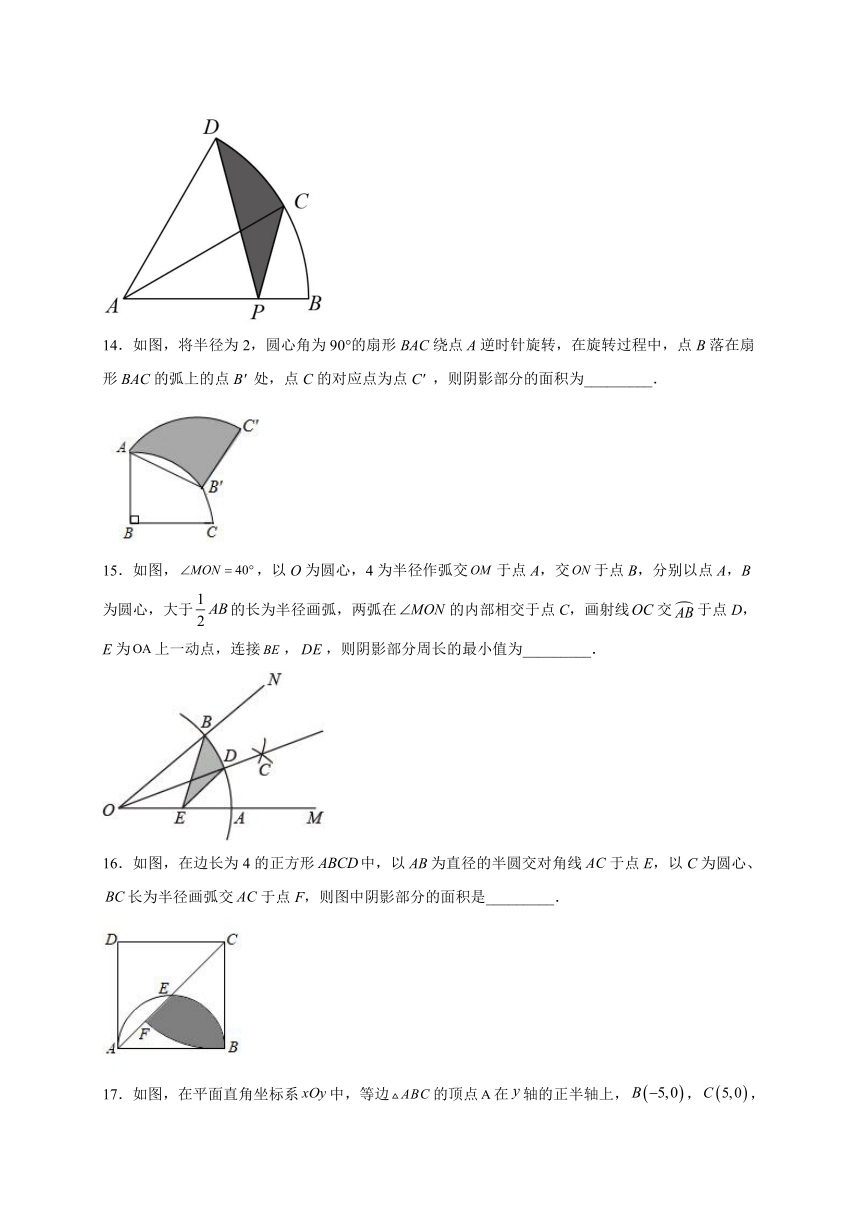
14.如图,将半径为2,圆心角为90°的扇形BAC绕点A逆时针旋转,在旋转过程中,点B落在扇形BAC的弧上的点B' 处,点C的对应点为点C' ,则阴影部分的面积为_________.
15.如图,,以O为圆心,4为半径作弧交于点A,交于点B,分别以点A,B为圆心,大于的长为半径画弧,两弧在的内部相交于点C,画射线交于点D,E为上一动点,连接,,则阴影部分周长的最小值为_________.
16.如图,在边长为4的正方形中,以为直径的半圆交对角线于点E,以C为圆心、长为半径画弧交于点F,则图中阴影部分的面积是_________.
17.如图,在平面直角坐标系中,等边的顶点在轴的正半轴上,,,点,将绕点顺时针旋转60°得到,则的长度为______,图中阴影部分面积为______.
三、解答题
18.设a,b,c是不全相等的任意实数,若.求证:x,y,z至少有一个大于零.
19.制造弯形管道时,经常要先按中心线计算“展直长度”,再下料,试计算如图所示的管道的展直长度L(结果取整数).
20.如图,在平面直角坐标系中,已知的三个顶点分别是A( 1,4),B( 3,2),C( 2,1).
(1)请画出关于原点的中心对称图形;
(2)请画出将绕点逆时针旋转90°后得到的;
(3)在(2)的条件下,求点旋转到点所经过的路线长(结果保留).
21.如图,已知是底角为30°的等腰三角形,B为AD上一点,以AB为直径的恰好过点C.
(1)判断直线CD与的位置关系,并说明理由;
(2)M为下半圆上的一个动点,若在某一时刻满足,已知半径等于2,求弧AM的长.
22.如图,中,,是的外接圆,的延长交边于点D.
(1)求证:;
(2)若,的半径为2,求劣弧的长.
23.如图,中,的平分线交于点O,以点O为圆心,长为半径作圆.
(1)求证:是的切线;
(2)若,求阴影部分面积.
试卷第1页,共3页
参考答案
1.A
【详解】
解:∵AD∥BC,
∴∠ABC+∠BAD=180°,
∵∠BAD=140°,
∴∠ABC=40°,
∵AB=AC,
∴∠ABC=∠ACB=40°,
∴∠BAC=180°-80°=100°,
∴的长=,
2.C
【详解】
解:如图,连接,
,即是斜边上的中线,
,
,
在中,,,
,
,
则分以下两种情况:
①如图,当时,是等腰三角形,
,
点与点重合,
点共线,
由圆周角定理得:,
则弧的长为;
②如图,当时,是等腰三角形,
,
由圆周角定理得:,
则弧的长为;
综上,弧的长为或,
3.A
【详解】
连接AD、DO,由折叠可知,
,,
∵,
∴,
∴是等边三角形,
∴,,
∵,
∴,
∴,
∴,
∴阴影部分的面积;
4.D
【详解】
解:连接,过点作于点,
四边形是平行四边形,,
四边形为菱形,
.
,
是等边三角形,
,
与为边长相等的两个等边三角形.
,
.
.
5.D
【详解】
解:取中点,连接、,
∵和中,,
∴在以为圆心,为直径的圆上,运动路径为,,
∴,
∴点运动路径长为.
6.B
【详解】
解:连接OB,OC,
∵△ABC是等边三角形,
∴∠BOC=2∠BAC=120°,
又∵AB=AC,OB=OC,OA=OA,
∴△AOB≌△AOC(SSS),
∴∠BAO=∠CAO=30°,
∴∠BOD=60°,
∴劣弧BD的长为=π,
故选B.
7.A
【详解】
解:由题意可得,三段弧是等弧,
,∠BCA=60°,
∴π=,
解得CB=3,
∵△ABC是等边三角形;
∴;
∴一个曲边三角形的面积是:[]×3+ =,
8.B
【详解】
解:连A1A5,A1A4,A1A3,作A6C⊥A1A5,如图,
∵六边形A1A2A3A4A5A6为正六边形,
∴A1A4=2a,∠A1A6A5=120°,A1A6=A5A6
∴∠HA1A6=30°,
∴A6H=a,A1H==a,
∴A1A5=A1A3=a,
当A1第一次滚动到图2位置时,顶点A1所经过的路径分别是以A2,A3,A4,A5,A6为圆心,以a,a,2a,a,a为半径,圆心角都为60°的五条弧,
∴顶点A1所经过的路径的长=++++=,
9.C
【详解】
解:∵2r+l=6,
∴l=6﹣2r,
∴圆锥的侧面积S侧=πrl=πr(6﹣2r)=﹣2π(r2﹣3r)=﹣2π[(r﹣)2﹣]=﹣2π(r﹣)2+π,
∴当r=时,S侧有最大值.
10.D
【详解】
解:如图,连接,,..
垂直平分,垂直平分,由“垂径定理的逆定理”可知,和都是的直径,
,,
四边形是平行四边形,
,
四边形是矩形,故(Ⅰ)正确,
观察图形可知当,
,
观察图形可知,这样的点不唯一(如下图所示),故(Ⅱ)错误,
11.
【详解】
解:设所在的圆的圆心为O,连接AB、OB、OC、OA,如图所示:
∵AD是棚高,
∴CD=BD=(m),AD⊥BC,,
∴O、D、A三点共线,∠AOB=∠AOC,
在Rt△ABD中,由勾股定理得:AB==4(m),
∴AB=2AD,
∴∠ABC=30°,
∴∠AOC=60°,
∴∠AOB=∠AOC=60°,
∴△ABO是等边三角形,
∴OB=OA=AB=4m,OD=OA﹣AD=4﹣2=2(m),∠COB=60°+60°=120°,
∴蔬菜大棚需要用塑料薄膜的面积===(m2),
故答案为:.
12.150
【详解】
设圆锥的母线长为l cm,扇形的圆心角为n°,
∵圆锥的底面圆周长为20πcm,
∴圆锥的侧面展开图扇形的弧长为20πcm,
由题意得:×20π×l=240π,
解得:l=24,
则=20π.
解得n=150,即扇形的圆心角为150°,
故答案为:150.
13.
【详解】
解:如图,作点C关于AB的对称点,
连接交OB于点,连接、,
此时最小,即,
由题意得,,
∴,
∴,
的长,
∴阴影部分周长的最小值为,
故答案为:.
14.
【详解】
解:连接BB’,过A作AF⊥BB’于F,则∠AFB=90°,如图,
∵将半径为2,圆心角为90°的扇形BAC绕点A逆时针旋转,在旋转过程中,点B落在扇形BAC的弧上的点B' 处,点C的对应点为点C' ,
∴扇形ABC和扇形AB’C’的面积相等,AB=AB’=BC=BB’=2,
∴△ABB’是等边三角形,
∴∠ABF=60°,
∴∠BAF=30°,
∴BF=AB=×2=1,由勾股定理得:AF=,
∴阴影部分的面积S=S扇形ABC (S扇形ABB’ S△ABB’)
=
=,
故答案为:.
15.
【详解】
解:由题意得:OC平分∠MON,
∴∠BOD=,
∴的长=,
作点D关于OM的对称点,连接B交OM于点,连接O,则B+ D= B+ =B,此时,BE+DE的最小值= B,
∵∠AO=∠AOD=∠BOD=20°,
∴∠BO=60 °,
∵O=OD=OB,
∴是等边三角形,
∴B=OB=4,
∴阴影部分周长的最小值=,
故答案是:.
16.3-6
【详解】
连接BE,
∵在正方形中,以为直径的半圆交对角线于点E,
∴∠AEB=90°,即:AC⊥BE,
∵∠CAB=45°,
∴是等腰直角三角形,即:AE=BE,
∴弓形BE的面积=,
∴阴影部分的面积=弓形BE的面积+扇形CBF的面积-的面积
=+-=3-6.
故答案是:3-6.
17.
【详解】
解:∵,,点,将绕点顺时针旋转60°得到,
∴BC=5-(-5)=10,∠BAC=60°,∠EAD=60°,DO=11,OC=5,
∴OA==,
∴AD==14,
∴==;
图中阴影部分面积为:=,
故答案为:,.
18.见解析.
【详解】
解:假设x,y,z都小于零,
则,
∴,
∴,
这与偶次方的非负性相矛盾,
∴假设不成立,
∴x,y,z至少有一个大于零.
19.
【详解】
解:由弧长公式,得的长.
展直长度.
答:图中所示的管道的展直长度是2970mm.
20.(1)见解析;(2)见解析;(3)
【详解】
解:(1)如图所示,为所求;
(2)如图所示,为所求;
(3)∵A( 1,4), C( 2,1),
∴,
∵,
∴点A旋转到点所经过的路线长为.
21.(1)相切,理由见解析;(2)
【详解】
(1)连接OC,
∵,
∴,
∴,
∴
∵OC为半径,
∴CD与圆O相切;
(2)连接OM
∵AB为直径,
∴,
∴
∴
∴
∴
∵
∴弧长.
22.(1)见解析;(2)
【详解】
(1)连接,
∵
∴
又∵O为的外心
∴垂直平分
又∵
∴
∴
(2)连接,
设,则
∴
∵
∴
∴
∵
∴
在中,
∴
∴
∴
∴劣弧的长为.
23.(1)见解析;(2)
【详解】
解:(1)证明:过O作于D,如图所示,
,
平分
,
为的半径,
为的半径,
是的切线.
(2)∵OD⊥AB,
∴∠ODB=90°,
∵∠CAO=30°,∠ACB=90°,
∴AC=OC=4,
∵∠AOC=90°-30°=60°,
∴∠COD=2∠AOC=120°,
由(1)得:AB是⊙O的切线,OC⊥AC,
∴AC为⊙O的切线,
∴AD=AC=4,
∴阴影部分面积=△AOC的面积+△AOD的面积-扇形OCD的面积
.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,四边形的顶点,,都在上,,,,则的弧长为( )
A. B. C. D.
2.如图,在中,,,斜边是半圆的直径,点是半圆上的一个动点,连接与交于点,若是等腰三角形,则弧的长为( )
A. B.或 C.或 D.或
3.如图,一张扇形纸片OAB,∠AOB=120°,OA=6,将这张扇形纸片折叠,使点A与点O重合,折痕为CD,则图中未重叠部分(即阴影部分)的面积为( )
A. B. C. D.
4.如图,扇形AOB中,OA=2,C为上的一点,连接AC,BC,如果四边形AOBC为平行四边形,则图中阴影部分的面积为( )
A. B. C. D.
5.如图,中,,,,点从点出发,沿运动到点停止,过点作射线的垂线,垂足为,点运动的路径长为( )
A. B. C. D.
6.如图,等边的三个顶点都在上,是的直径.若,则劣弧的长是( )
A. B. C. D.
7.如图,所示的曲边三角形可按下述方法作出:作等边三角形ABC;分别以点A,B,C为圆心,以AB的长为半径作弧BC,弧AC,弧AB,三段弧所围成的图形就是一个曲边三角形,如果一个曲边三角形的周长为3π,则它的面积为( )
A. B. C. D.
8.如图,将边长为的正六边形在直线l上由图的位置按顺时针方向向右作无滑动滚动,当正六边形旋转一周滚动到图位置时,顶点所经过的路径( )
A. B. C. D.
9.设圆锥的底面圆半径为r,圆锥的母线长为l,满足2r+l=6,这样的圆锥的侧面积( )
A.有最大值π B.有最小值π C.有最大值π D.有最小值π
10.如图,等腰△AOB中,顶角∠AOB=40°,用尺规按①到④的步骤操作:
①以O为圆心,OA为半径画圆;
②在⊙O上任取一点P(不与点A,B重合),连接AP;
③作AB的垂直平分线与⊙O交于M,N;
④作AP的垂直平分线与⊙O交于E,F.
结论Ⅰ:顺次连接M,E,N,F四点必能得到矩形;
结论Ⅱ:⊙O上只有唯一的点P,使得S扇形FOM=S扇形AOB.
对于结论Ⅰ和Ⅱ,下列判断正确的是( )
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对 C.Ⅰ不对Ⅱ对 D.Ⅰ对Ⅱ不对
二、填空题
11.为了贯彻习近平总书记“促进乡村全面振兴、实现农业农村现代化”的指示,某农机组织推广建立横截面为弓形的一种全新的全封闭式塑料薄膜蔬菜大棚,如图所示,已知棚高AD=2m,底部BC=m,大棚的长度BE=30m,如果不考虑塑料薄膜接头重合及埋在土里的部分,那么搭建一个这样的蔬菜大棚需要用塑料薄膜的面积是_______m2.
12.如图,要用一个扇形纸片围成一个无底盖的圆锥(接缝处忽略不计),若该圆锥的底面圆周长为cm,侧面积为,则这个扇形的圆心角的度数是__________度.
13.如图,在扇形中,,平分交弧于点,点为半径上一动点,若,则阴影部分周长的最小值为___________.
14.如图,将半径为2,圆心角为90°的扇形BAC绕点A逆时针旋转,在旋转过程中,点B落在扇形BAC的弧上的点B' 处,点C的对应点为点C' ,则阴影部分的面积为_________.
15.如图,,以O为圆心,4为半径作弧交于点A,交于点B,分别以点A,B为圆心,大于的长为半径画弧,两弧在的内部相交于点C,画射线交于点D,E为上一动点,连接,,则阴影部分周长的最小值为_________.
16.如图,在边长为4的正方形中,以为直径的半圆交对角线于点E,以C为圆心、长为半径画弧交于点F,则图中阴影部分的面积是_________.
17.如图,在平面直角坐标系中,等边的顶点在轴的正半轴上,,,点,将绕点顺时针旋转60°得到,则的长度为______,图中阴影部分面积为______.
三、解答题
18.设a,b,c是不全相等的任意实数,若.求证:x,y,z至少有一个大于零.
19.制造弯形管道时,经常要先按中心线计算“展直长度”,再下料,试计算如图所示的管道的展直长度L(结果取整数).
20.如图,在平面直角坐标系中,已知的三个顶点分别是A( 1,4),B( 3,2),C( 2,1).
(1)请画出关于原点的中心对称图形;
(2)请画出将绕点逆时针旋转90°后得到的;
(3)在(2)的条件下,求点旋转到点所经过的路线长(结果保留).
21.如图,已知是底角为30°的等腰三角形,B为AD上一点,以AB为直径的恰好过点C.
(1)判断直线CD与的位置关系,并说明理由;
(2)M为下半圆上的一个动点,若在某一时刻满足,已知半径等于2,求弧AM的长.
22.如图,中,,是的外接圆,的延长交边于点D.
(1)求证:;
(2)若,的半径为2,求劣弧的长.
23.如图,中,的平分线交于点O,以点O为圆心,长为半径作圆.
(1)求证:是的切线;
(2)若,求阴影部分面积.
试卷第1页,共3页
参考答案
1.A
【详解】
解:∵AD∥BC,
∴∠ABC+∠BAD=180°,
∵∠BAD=140°,
∴∠ABC=40°,
∵AB=AC,
∴∠ABC=∠ACB=40°,
∴∠BAC=180°-80°=100°,
∴的长=,
2.C
【详解】
解:如图,连接,
,即是斜边上的中线,
,
,
在中,,,
,
,
则分以下两种情况:
①如图,当时,是等腰三角形,
,
点与点重合,
点共线,
由圆周角定理得:,
则弧的长为;
②如图,当时,是等腰三角形,
,
由圆周角定理得:,
则弧的长为;
综上,弧的长为或,
3.A
【详解】
连接AD、DO,由折叠可知,
,,
∵,
∴,
∴是等边三角形,
∴,,
∵,
∴,
∴,
∴,
∴阴影部分的面积;
4.D
【详解】
解:连接,过点作于点,
四边形是平行四边形,,
四边形为菱形,
.
,
是等边三角形,
,
与为边长相等的两个等边三角形.
,
.
.
5.D
【详解】
解:取中点,连接、,
∵和中,,
∴在以为圆心,为直径的圆上,运动路径为,,
∴,
∴点运动路径长为.
6.B
【详解】
解:连接OB,OC,
∵△ABC是等边三角形,
∴∠BOC=2∠BAC=120°,
又∵AB=AC,OB=OC,OA=OA,
∴△AOB≌△AOC(SSS),
∴∠BAO=∠CAO=30°,
∴∠BOD=60°,
∴劣弧BD的长为=π,
故选B.
7.A
【详解】
解:由题意可得,三段弧是等弧,
,∠BCA=60°,
∴π=,
解得CB=3,
∵△ABC是等边三角形;
∴;
∴一个曲边三角形的面积是:[]×3+ =,
8.B
【详解】
解:连A1A5,A1A4,A1A3,作A6C⊥A1A5,如图,
∵六边形A1A2A3A4A5A6为正六边形,
∴A1A4=2a,∠A1A6A5=120°,A1A6=A5A6
∴∠HA1A6=30°,
∴A6H=a,A1H==a,
∴A1A5=A1A3=a,
当A1第一次滚动到图2位置时,顶点A1所经过的路径分别是以A2,A3,A4,A5,A6为圆心,以a,a,2a,a,a为半径,圆心角都为60°的五条弧,
∴顶点A1所经过的路径的长=++++=,
9.C
【详解】
解:∵2r+l=6,
∴l=6﹣2r,
∴圆锥的侧面积S侧=πrl=πr(6﹣2r)=﹣2π(r2﹣3r)=﹣2π[(r﹣)2﹣]=﹣2π(r﹣)2+π,
∴当r=时,S侧有最大值.
10.D
【详解】
解:如图,连接,,..
垂直平分,垂直平分,由“垂径定理的逆定理”可知,和都是的直径,
,,
四边形是平行四边形,
,
四边形是矩形,故(Ⅰ)正确,
观察图形可知当,
,
观察图形可知,这样的点不唯一(如下图所示),故(Ⅱ)错误,
11.
【详解】
解:设所在的圆的圆心为O,连接AB、OB、OC、OA,如图所示:
∵AD是棚高,
∴CD=BD=(m),AD⊥BC,,
∴O、D、A三点共线,∠AOB=∠AOC,
在Rt△ABD中,由勾股定理得:AB==4(m),
∴AB=2AD,
∴∠ABC=30°,
∴∠AOC=60°,
∴∠AOB=∠AOC=60°,
∴△ABO是等边三角形,
∴OB=OA=AB=4m,OD=OA﹣AD=4﹣2=2(m),∠COB=60°+60°=120°,
∴蔬菜大棚需要用塑料薄膜的面积===(m2),
故答案为:.
12.150
【详解】
设圆锥的母线长为l cm,扇形的圆心角为n°,
∵圆锥的底面圆周长为20πcm,
∴圆锥的侧面展开图扇形的弧长为20πcm,
由题意得:×20π×l=240π,
解得:l=24,
则=20π.
解得n=150,即扇形的圆心角为150°,
故答案为:150.
13.
【详解】
解:如图,作点C关于AB的对称点,
连接交OB于点,连接、,
此时最小,即,
由题意得,,
∴,
∴,
的长,
∴阴影部分周长的最小值为,
故答案为:.
14.
【详解】
解:连接BB’,过A作AF⊥BB’于F,则∠AFB=90°,如图,
∵将半径为2,圆心角为90°的扇形BAC绕点A逆时针旋转,在旋转过程中,点B落在扇形BAC的弧上的点B' 处,点C的对应点为点C' ,
∴扇形ABC和扇形AB’C’的面积相等,AB=AB’=BC=BB’=2,
∴△ABB’是等边三角形,
∴∠ABF=60°,
∴∠BAF=30°,
∴BF=AB=×2=1,由勾股定理得:AF=,
∴阴影部分的面积S=S扇形ABC (S扇形ABB’ S△ABB’)
=
=,
故答案为:.
15.
【详解】
解:由题意得:OC平分∠MON,
∴∠BOD=,
∴的长=,
作点D关于OM的对称点,连接B交OM于点,连接O,则B+ D= B+ =B,此时,BE+DE的最小值= B,
∵∠AO=∠AOD=∠BOD=20°,
∴∠BO=60 °,
∵O=OD=OB,
∴是等边三角形,
∴B=OB=4,
∴阴影部分周长的最小值=,
故答案是:.
16.3-6
【详解】
连接BE,
∵在正方形中,以为直径的半圆交对角线于点E,
∴∠AEB=90°,即:AC⊥BE,
∵∠CAB=45°,
∴是等腰直角三角形,即:AE=BE,
∴弓形BE的面积=,
∴阴影部分的面积=弓形BE的面积+扇形CBF的面积-的面积
=+-=3-6.
故答案是:3-6.
17.
【详解】
解:∵,,点,将绕点顺时针旋转60°得到,
∴BC=5-(-5)=10,∠BAC=60°,∠EAD=60°,DO=11,OC=5,
∴OA==,
∴AD==14,
∴==;
图中阴影部分面积为:=,
故答案为:,.
18.见解析.
【详解】
解:假设x,y,z都小于零,
则,
∴,
∴,
这与偶次方的非负性相矛盾,
∴假设不成立,
∴x,y,z至少有一个大于零.
19.
【详解】
解:由弧长公式,得的长.
展直长度.
答:图中所示的管道的展直长度是2970mm.
20.(1)见解析;(2)见解析;(3)
【详解】
解:(1)如图所示,为所求;
(2)如图所示,为所求;
(3)∵A( 1,4), C( 2,1),
∴,
∵,
∴点A旋转到点所经过的路线长为.
21.(1)相切,理由见解析;(2)
【详解】
(1)连接OC,
∵,
∴,
∴,
∴
∵OC为半径,
∴CD与圆O相切;
(2)连接OM
∵AB为直径,
∴,
∴
∴
∴
∴
∵
∴弧长.
22.(1)见解析;(2)
【详解】
(1)连接,
∵
∴
又∵O为的外心
∴垂直平分
又∵
∴
∴
(2)连接,
设,则
∴
∵
∴
∴
∵
∴
在中,
∴
∴
∴
∴劣弧的长为.
23.(1)见解析;(2)
【详解】
解:(1)证明:过O作于D,如图所示,
,
平分
,
为的半径,
为的半径,
是的切线.
(2)∵OD⊥AB,
∴∠ODB=90°,
∵∠CAO=30°,∠ACB=90°,
∴AC=OC=4,
∵∠AOC=90°-30°=60°,
∴∠COD=2∠AOC=120°,
由(1)得:AB是⊙O的切线,OC⊥AC,
∴AC为⊙O的切线,
∴AD=AC=4,
∴阴影部分面积=△AOC的面积+△AOD的面积-扇形OCD的面积
.
答案第1页,共2页
答案第1页,共2页
同课章节目录
