2020-2021学年人教版九年级数学下册27.1图形的相似知识点分类训练(word版、含答案)
文档属性
| 名称 | 2020-2021学年人教版九年级数学下册27.1图形的相似知识点分类训练(word版、含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 182.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 00:00:00 | ||
图片预览




文档简介
2021-2022学年人教版九年级数学下册《27.1图形的相似》知识点分类训练(附答案)
一.比例的性质
1.如果实数a,b,c,d满足=,下列四个选项中,正确的是( )
A.= B.= C.= D.=
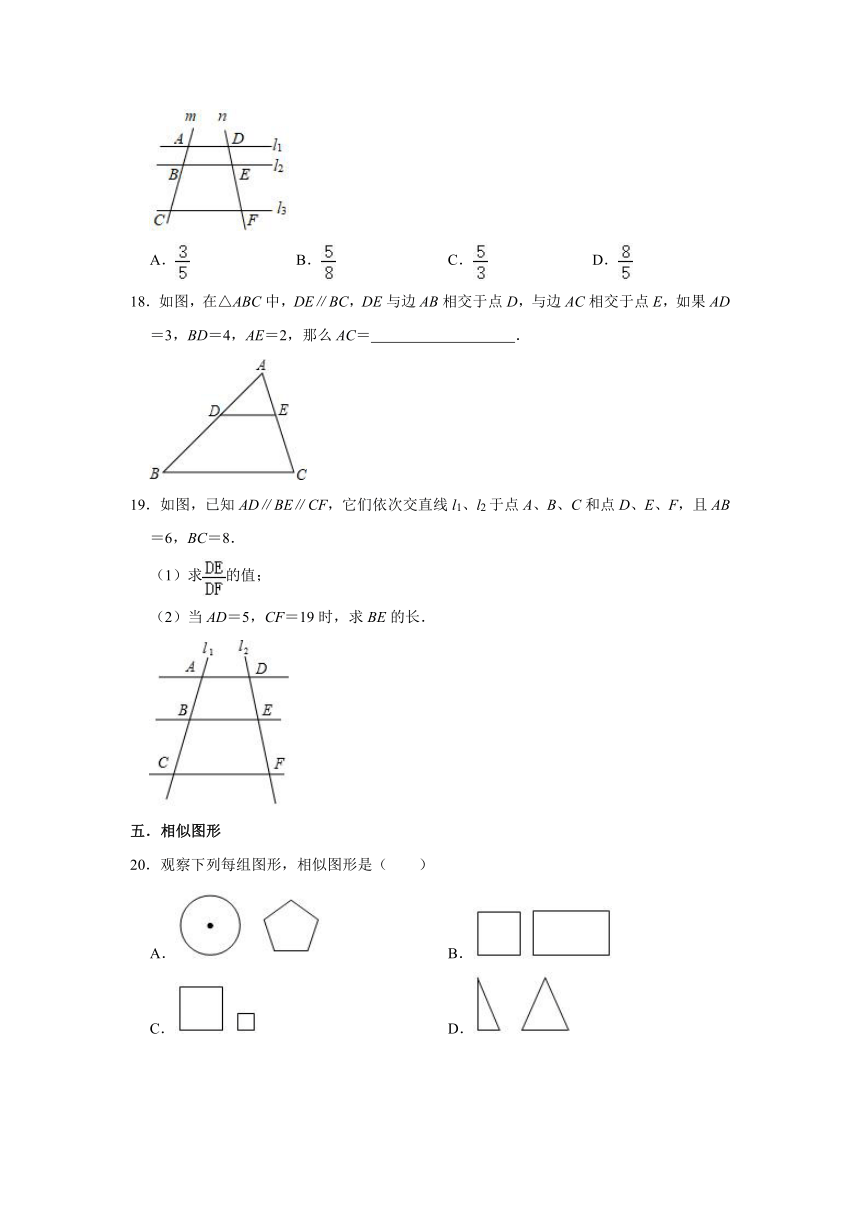
2.如果A:B=5:3,B:C=1.5:4.那么A:C=( )
A.5:8 B.4:5 C.8:5 D.5:4
3.若,则的值为( )
A. B.5 C. D.
4.若=,则= .
5.如果,那么= .
6.已知:a:b=:,b:c=2:5,求:a:b:c(化成最简整数比)
7.已知a:b=2:3,b:c=3:4,且2a+b﹣c=6,求a、b、c的值.
二.比例线段
8.若ad=bc(b≠d)且a,b,c,d均为正数,则下列结论不成立的是( )
A. B.
C. D.
9.如果ab=cd,则下列正确的是( )
A.a:b=c:d B.a:c=d:b C.a:d=b:c D.d:c=a:b
10.已知四个非零实数a,b,c,d成比例,即,下列各式中不一定成立的是( )
A. B. C. D.
11.已知线段a=4,b=16,线段c是a,b的比例中项,那么c等于 .
12.在一张地图上量得上海与南京两地的距离为3.2厘米,又已知上海与南京、北京两地的实际距离分别约为300千米和1080千米,那么在这张地图上,上海与北京两地的距离为多少厘米?
三.黄金分割
13.如图,在△ABC中,∠A=36°,AB=AC,以点B为圆心任意长为半径画弧,分别交AB,BC于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点O,连接BO,并延长交AC于点D,若AB=2,则CD的长为( )
A.﹣1 B.3﹣ C.+1 D.3+
14.若点C为线段AB的黄金分割点,且AC>BC.则下列各式中不正确的是( )
A.AC=AB B.BC=AB
C.AB=AC D.AB:AC=AC:BC
15.已知线段MN的长为4,点P是线段MN的黄金分割点,那么较长线段MP的长是 .
16.如图,在△ABC中,点D在边AB上,且BD=DC=AC,已知∠ACE=108°,BC=2.
(1)求∠B的度数;
(2)我们把有一个内角等于36°的等腰三角形称为黄金三角形.它的腰长与底边长的比(或者底边长与腰长的比)等于黄金比.
①写出图中所有的黄金三角形,选一个说明理由;
②求AD的长.
四.平行线分线段成比例
17.如图,已知直线l1∥l2∥l3,直线m、n分别与直线l1、l2、l3分别交于点A、B、C、D、E、F,若DE=3,DF=8,则的值为( )
A. B. C. D.
18.如图,在△ABC中,DE∥BC,DE与边AB相交于点D,与边AC相交于点E,如果AD=3,BD=4,AE=2,那么AC= .
19.如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F,且AB=6,BC=8.
(1)求的值;
(2)当AD=5,CF=19时,求BE的长.
五.相似图形
20.观察下列每组图形,相似图形是( )
A. B.
C. D.
参考答案
一.比例的性质
1.解:A、∵=,∴=,故选项正确;
B、当a+b=c+d=0时,等式不成立,故选项错误;
C、当b+d=0时,等式不成立,故选项错误;
D、无法得到=,故选项错误.
故选:A.
2.解:∵A:B=5:3,
∴A=B,
∵B:C=1.5:4.
∴C=B,
∴A:C=B:B=5:8.
故选:A.
3.解:∵,
∴=1+=1+=.
故选:C.
4.解:∵=,
∴﹣1=,
∴=.
故答案为:.
5.解:∵,
∴设a=3k,b=4k(k≠0),
∴==.
故答案为:.
6.解:∵a:b=:=3:4,b:c=2:5=4:10,
∴a:b:c=3:4:10.
7.解:∵a:b=2:3,b:c=3:4,
∴设a=2k,b=3k,c=4k(k≠0),
∵2a+b﹣c=6,
∴4k+3k﹣4k=6,
∴k=2,
∴a=2k=2×2=4,
b=3k=3×2=6,
c=4k=4×2=8.
二.比例线段
8.解:由ad=bc(b≠d)且a,b,c,d均为正数,
可得:,故A正确;
∴,故B正确;
∴,故D正确;
不能得出,故C错误;
故选:C.
9.解:∵ab=cd,
∴a:c=d:b,
故选:B.
10.解:∵,
∴ad=bc,
A、=的两个内项是a、d,两个外项是b、c,所以ad=bc,不符合题意;
B、=的两个内项是a、d,两个外项是b、c,所以ad=bc,不符合题意;
C、∵,∴=,不符合题意;
D、=的两个内项是a、c,两个外项是b、d,所以ac=bd,符合题意.
故选:D.
11.解:∵线段c是a、b的比例中项,
∴c2=ab=64,
解得:c=±8,
又∵线段是正数,
∴c=8.
故答案为:8.
12.解:设在这张地图上,上海与北京两地的距离为x厘米.根据题意得到:.
解得x=11.52,
答:在这张地图上,上海与北京两地的距离为11.52厘米.
三.黄金分割
13.解:∵∠A=36°,AB=AC=2,
∴∠ABC=∠C=(180°﹣36°)=72°,
由题意得:BD平分∠ABC,
∴∠ABD=∠CBD=∠ABC=36°,
∴∠ABD=∠A,∠BDC=∠A+∠ABD=72°=∠C,
∴AD=BD=BC,△BCD∽△ABC,
∴=,∴=,
∴点D是AC的黄金分割点,AD>CD,
∴AD=AC=﹣1,
∴CD=AC﹣AD=3﹣,
故选:B.
14.解:∵点C为线段AB的黄金分割点,且AC>BC,
∴AC=AB,AB:AC=AC:BC,
∴AB=AC,BC=AB﹣AC=AB,
故选项A符合题意,选项B、C、D不符合题意;
故选:A.
15.解:∵线段MN的长为4,点P是线段MN的黄金分割点,MP>NP,
∴MP=MN=×4=2﹣2,
故答案为:2﹣2.
16.解:(1)设∠B=x,
∵BD=DC,
∴∠DCB=∠B=x,
∴∠ADC=∠B+∠DCB=2x,
∵AC=DC,
∴∠A=∠ADC=2x,
∵∠ACE=∠B+∠A,
∴x+2x=108°,解得x=36°,
即∠B的度数为36°;
(2)①△ABC、△DBC、△CAD都是黄金三角形.
理由如下:∵DB=DC,∠B=36°,
∴△DBC为黄金三角形;
∵∠BCA=180°﹣∠ACE=72°,
而∠A=2×36°=72°,
∴∠A=∠ACB,
而∠B=36°,
∴△ABC为黄金三角形;
∵∠ACD=∠ACB﹣∠DCB=72°﹣36°=36°,
而CA=CD,
∴△CAD为黄金三角形;
②∵△BAC为黄金三角形,
∴=,
而BC=2,
∴AC=﹣1,
∴CD=CA=﹣1,
∴BD=CD=﹣1,
∴AD=AB﹣BD=2﹣(﹣1)=3﹣.
四.平行线分线段成比例
17.解:∵l1∥l2∥l3,
∴,
∵DE=3,DF=8,
∴,
即=,
故选:B.
18.解:∵DE∥BC,
∴=,
∵AD=3,BD=4,AE=2,
∴=,
解得EC=,
∴AC=AE+EC=2+=,
故答案为:.
19.解:(1)∵AD∥BE∥CF,
∴===;
(2)过D点作DM∥AC交CF于M,交BE于N,如图,
∵AD∥BN∥CM,AC∥DM,
∴四边形ABND和四边形ACMD都是平行四边形,
∴BN=AD=5,CM=AD=5,
∴MF=CF﹣CM=19﹣5=14,
∵NE∥MF,
∴==,
∴NE=MF=×14=6,
∴BE=BN+NE=5+6=11.
五.相似图形
20.解:A、两图形形状不同,故不是相似图形;
B、两图形形状不同,故不是相似图形;
C、两图形形状相同,故是相似图形;
D、两图形形状不同,故不是相似图形;
故选:C.
一.比例的性质
1.如果实数a,b,c,d满足=,下列四个选项中,正确的是( )
A.= B.= C.= D.=
2.如果A:B=5:3,B:C=1.5:4.那么A:C=( )
A.5:8 B.4:5 C.8:5 D.5:4
3.若,则的值为( )
A. B.5 C. D.
4.若=,则= .
5.如果,那么= .
6.已知:a:b=:,b:c=2:5,求:a:b:c(化成最简整数比)
7.已知a:b=2:3,b:c=3:4,且2a+b﹣c=6,求a、b、c的值.
二.比例线段
8.若ad=bc(b≠d)且a,b,c,d均为正数,则下列结论不成立的是( )
A. B.
C. D.
9.如果ab=cd,则下列正确的是( )
A.a:b=c:d B.a:c=d:b C.a:d=b:c D.d:c=a:b
10.已知四个非零实数a,b,c,d成比例,即,下列各式中不一定成立的是( )
A. B. C. D.
11.已知线段a=4,b=16,线段c是a,b的比例中项,那么c等于 .
12.在一张地图上量得上海与南京两地的距离为3.2厘米,又已知上海与南京、北京两地的实际距离分别约为300千米和1080千米,那么在这张地图上,上海与北京两地的距离为多少厘米?
三.黄金分割
13.如图,在△ABC中,∠A=36°,AB=AC,以点B为圆心任意长为半径画弧,分别交AB,BC于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点O,连接BO,并延长交AC于点D,若AB=2,则CD的长为( )
A.﹣1 B.3﹣ C.+1 D.3+
14.若点C为线段AB的黄金分割点,且AC>BC.则下列各式中不正确的是( )
A.AC=AB B.BC=AB
C.AB=AC D.AB:AC=AC:BC
15.已知线段MN的长为4,点P是线段MN的黄金分割点,那么较长线段MP的长是 .
16.如图,在△ABC中,点D在边AB上,且BD=DC=AC,已知∠ACE=108°,BC=2.
(1)求∠B的度数;
(2)我们把有一个内角等于36°的等腰三角形称为黄金三角形.它的腰长与底边长的比(或者底边长与腰长的比)等于黄金比.
①写出图中所有的黄金三角形,选一个说明理由;
②求AD的长.
四.平行线分线段成比例
17.如图,已知直线l1∥l2∥l3,直线m、n分别与直线l1、l2、l3分别交于点A、B、C、D、E、F,若DE=3,DF=8,则的值为( )
A. B. C. D.
18.如图,在△ABC中,DE∥BC,DE与边AB相交于点D,与边AC相交于点E,如果AD=3,BD=4,AE=2,那么AC= .
19.如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F,且AB=6,BC=8.
(1)求的值;
(2)当AD=5,CF=19时,求BE的长.
五.相似图形
20.观察下列每组图形,相似图形是( )
A. B.
C. D.
参考答案
一.比例的性质
1.解:A、∵=,∴=,故选项正确;
B、当a+b=c+d=0时,等式不成立,故选项错误;
C、当b+d=0时,等式不成立,故选项错误;
D、无法得到=,故选项错误.
故选:A.
2.解:∵A:B=5:3,
∴A=B,
∵B:C=1.5:4.
∴C=B,
∴A:C=B:B=5:8.
故选:A.
3.解:∵,
∴=1+=1+=.
故选:C.
4.解:∵=,
∴﹣1=,
∴=.
故答案为:.
5.解:∵,
∴设a=3k,b=4k(k≠0),
∴==.
故答案为:.
6.解:∵a:b=:=3:4,b:c=2:5=4:10,
∴a:b:c=3:4:10.
7.解:∵a:b=2:3,b:c=3:4,
∴设a=2k,b=3k,c=4k(k≠0),
∵2a+b﹣c=6,
∴4k+3k﹣4k=6,
∴k=2,
∴a=2k=2×2=4,
b=3k=3×2=6,
c=4k=4×2=8.
二.比例线段
8.解:由ad=bc(b≠d)且a,b,c,d均为正数,
可得:,故A正确;
∴,故B正确;
∴,故D正确;
不能得出,故C错误;
故选:C.
9.解:∵ab=cd,
∴a:c=d:b,
故选:B.
10.解:∵,
∴ad=bc,
A、=的两个内项是a、d,两个外项是b、c,所以ad=bc,不符合题意;
B、=的两个内项是a、d,两个外项是b、c,所以ad=bc,不符合题意;
C、∵,∴=,不符合题意;
D、=的两个内项是a、c,两个外项是b、d,所以ac=bd,符合题意.
故选:D.
11.解:∵线段c是a、b的比例中项,
∴c2=ab=64,
解得:c=±8,
又∵线段是正数,
∴c=8.
故答案为:8.
12.解:设在这张地图上,上海与北京两地的距离为x厘米.根据题意得到:.
解得x=11.52,
答:在这张地图上,上海与北京两地的距离为11.52厘米.
三.黄金分割
13.解:∵∠A=36°,AB=AC=2,
∴∠ABC=∠C=(180°﹣36°)=72°,
由题意得:BD平分∠ABC,
∴∠ABD=∠CBD=∠ABC=36°,
∴∠ABD=∠A,∠BDC=∠A+∠ABD=72°=∠C,
∴AD=BD=BC,△BCD∽△ABC,
∴=,∴=,
∴点D是AC的黄金分割点,AD>CD,
∴AD=AC=﹣1,
∴CD=AC﹣AD=3﹣,
故选:B.
14.解:∵点C为线段AB的黄金分割点,且AC>BC,
∴AC=AB,AB:AC=AC:BC,
∴AB=AC,BC=AB﹣AC=AB,
故选项A符合题意,选项B、C、D不符合题意;
故选:A.
15.解:∵线段MN的长为4,点P是线段MN的黄金分割点,MP>NP,
∴MP=MN=×4=2﹣2,
故答案为:2﹣2.
16.解:(1)设∠B=x,
∵BD=DC,
∴∠DCB=∠B=x,
∴∠ADC=∠B+∠DCB=2x,
∵AC=DC,
∴∠A=∠ADC=2x,
∵∠ACE=∠B+∠A,
∴x+2x=108°,解得x=36°,
即∠B的度数为36°;
(2)①△ABC、△DBC、△CAD都是黄金三角形.
理由如下:∵DB=DC,∠B=36°,
∴△DBC为黄金三角形;
∵∠BCA=180°﹣∠ACE=72°,
而∠A=2×36°=72°,
∴∠A=∠ACB,
而∠B=36°,
∴△ABC为黄金三角形;
∵∠ACD=∠ACB﹣∠DCB=72°﹣36°=36°,
而CA=CD,
∴△CAD为黄金三角形;
②∵△BAC为黄金三角形,
∴=,
而BC=2,
∴AC=﹣1,
∴CD=CA=﹣1,
∴BD=CD=﹣1,
∴AD=AB﹣BD=2﹣(﹣1)=3﹣.
四.平行线分线段成比例
17.解:∵l1∥l2∥l3,
∴,
∵DE=3,DF=8,
∴,
即=,
故选:B.
18.解:∵DE∥BC,
∴=,
∵AD=3,BD=4,AE=2,
∴=,
解得EC=,
∴AC=AE+EC=2+=,
故答案为:.
19.解:(1)∵AD∥BE∥CF,
∴===;
(2)过D点作DM∥AC交CF于M,交BE于N,如图,
∵AD∥BN∥CM,AC∥DM,
∴四边形ABND和四边形ACMD都是平行四边形,
∴BN=AD=5,CM=AD=5,
∴MF=CF﹣CM=19﹣5=14,
∵NE∥MF,
∴==,
∴NE=MF=×14=6,
∴BE=BN+NE=5+6=11.
五.相似图形
20.解:A、两图形形状不同,故不是相似图形;
B、两图形形状不同,故不是相似图形;
C、两图形形状相同,故是相似图形;
D、两图形形状不同,故不是相似图形;
故选:C.
