北师大版高中数学必修2《空间两点间的距离公式》参考课件(共22张PPT)
文档属性
| 名称 | 北师大版高中数学必修2《空间两点间的距离公式》参考课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 519.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 00:00:00 | ||
图片预览

文档简介
(共22张PPT)
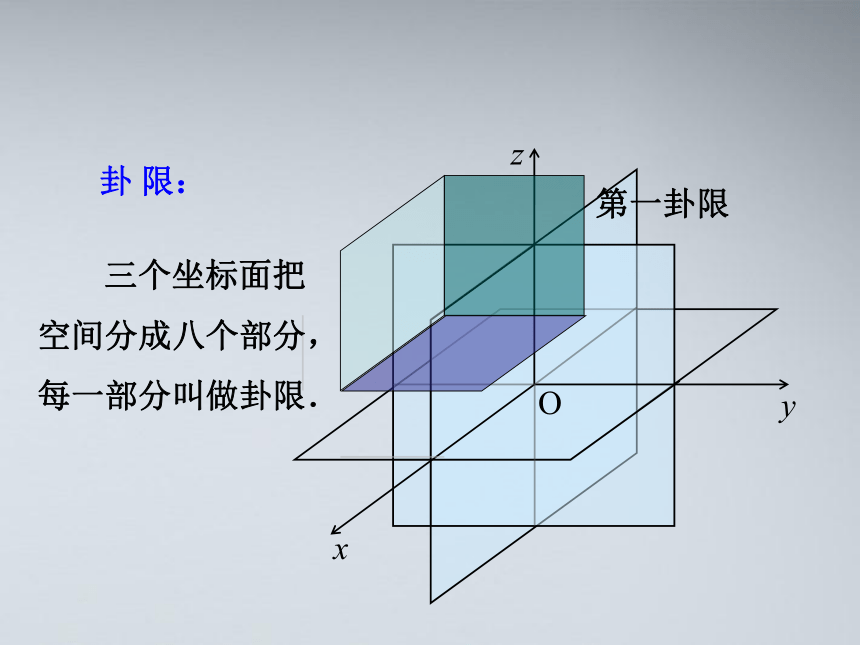
O
z
y
x
第一卦限
卦 限:
三个坐标面把
空间分成八个部分,
每一部分叫做卦限.
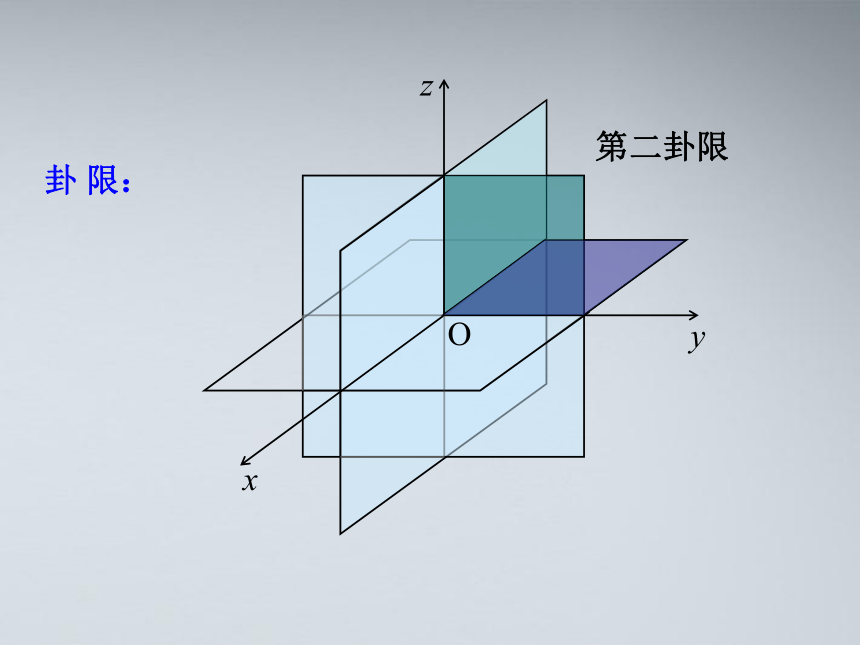
O
z
y
x
第二卦限
卦 限:
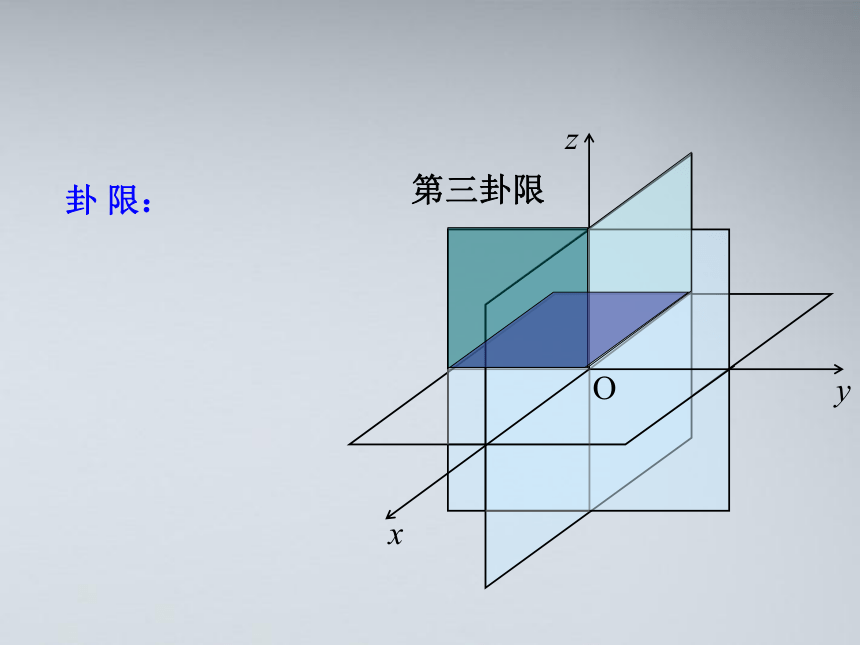
第三卦限
O
z
y
x
卦 限:
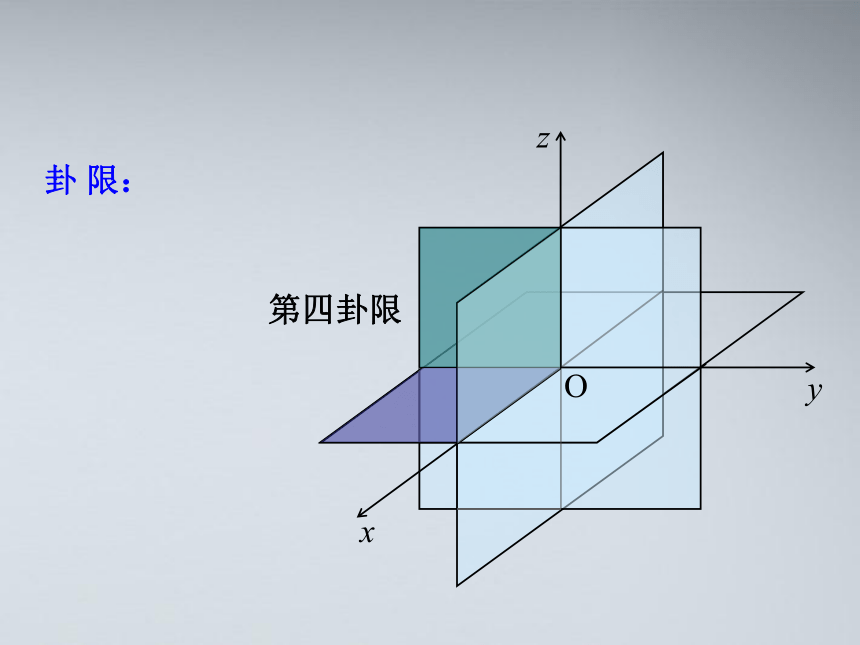
O
z
y
x
第四卦限
卦 限:
O
z
y
x
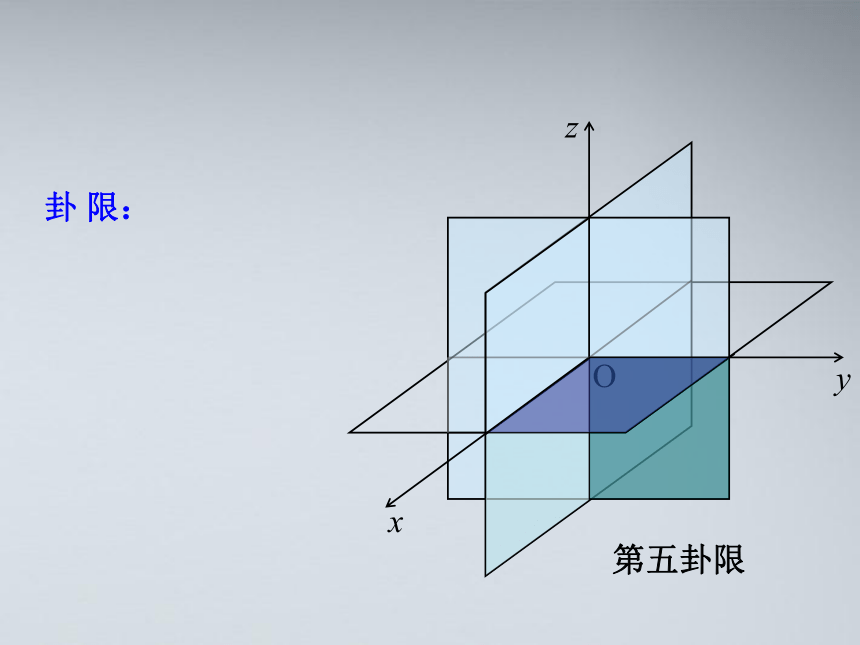
第五卦限
卦 限:
O
z
y
x
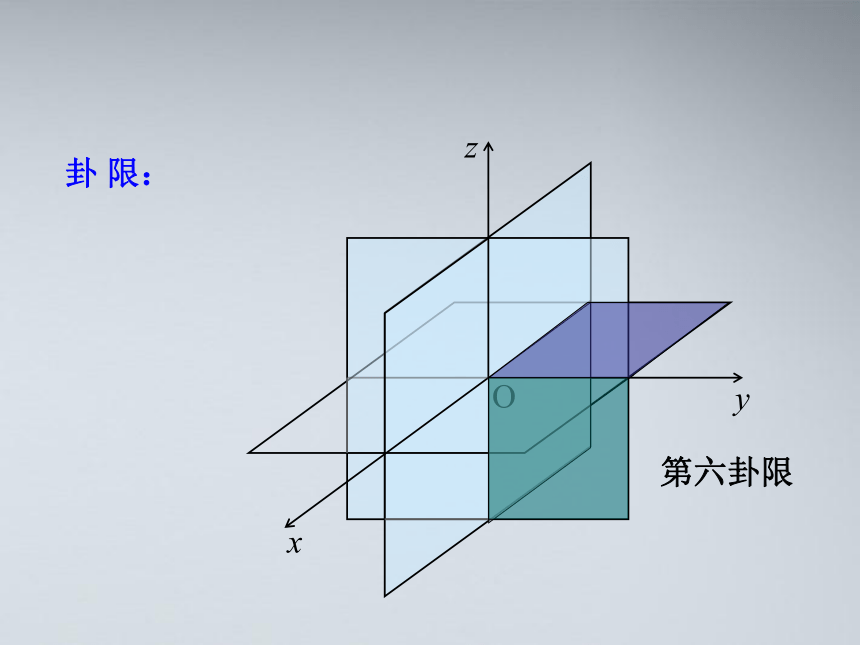
第六卦限
卦 限:
O
z
y
x
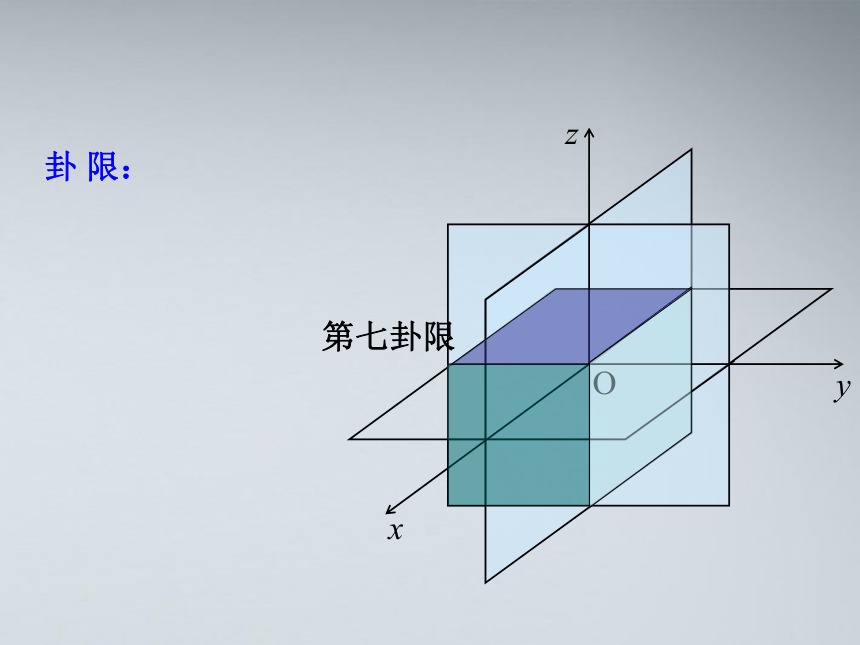
第七卦限
卦 限:
O
z
y
x
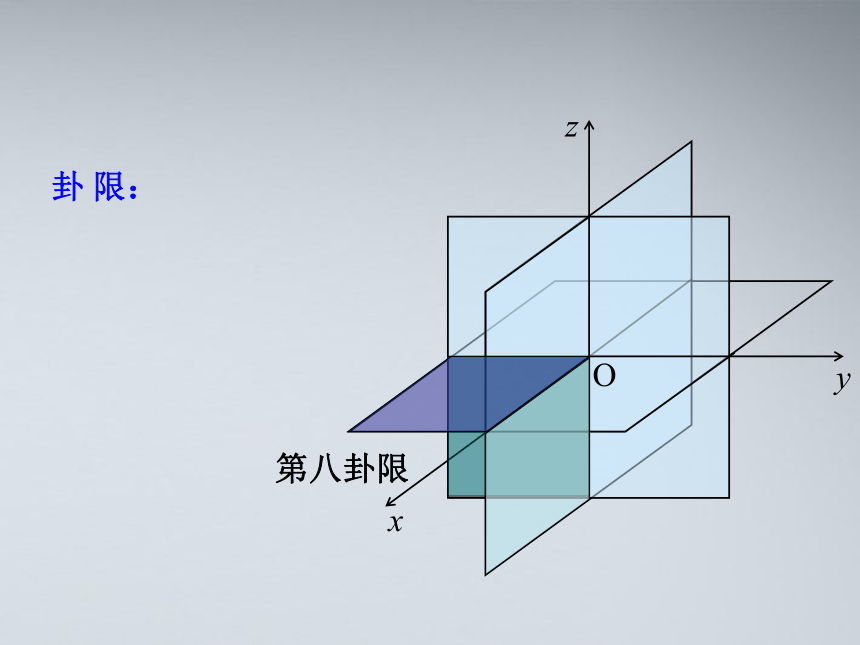
第八卦限
卦 限:
3.3空间两点间的距离公式
问题1:长方体的对角线是长方体中的那一条线段?
问题2:怎样测量长方体的对角线的长?
问题3:已知长方体的长、宽、高分别是a、b、c,则对角线的长
问题4:给出空间两点A(x1,y1,z1),P(x2,y2,z2)
可否类比得到一个距离公式?
1、设O(0,0,0),P(x0,y0,z0)则
x
y
z
o
P
A
B
C
O
x
y
z
设M 1(x 1,y 1,z 1)、M 2(x 2,y 2,z 2)为空间两点.
与x 轴平行的边的边长为|x 2 x 1|,
作一个以M 1和M 2为对角线顶点的长方体,使其三个相邻的面分别平行于三个坐标面.
M 1
M 2
P
Q
x 2
x 1
与y 轴平行的边的边长为|y 2 y 1|,
y 2
y 1
O
x
y
z
M 1
M 2
P
Q
设M 1(x 1,y 1,z 1)、M 2(x 2,y 2,z 2)为空间两点.
与x 轴平行的边的边长为|x 2 x 1|,
作一个以M 1和M 2为对角线顶点的长方体,使其三个相邻的面分别平行于三个坐标面.
与z 轴平行的边的边长为|z 2 z 1|.
z 2
z 1
O
x
y
z
M 1
M 2
P
Q
与y 轴平行的边的边长为|y 2 y 1|,
设M 1(x 1,y 1,z 1)、M 2(x 2,y 2,z 2)为空间两点.
与x 轴平行的边的边长为|x 2 x 1|,
作一个以M 1和M 2为对角线顶点的长方体,使其三个相邻的面分别平行于三个坐标.
因为
| M1M2 | 2
= | M1Q | 2 + | M2Q | 2
= | M1P | 2 + | PQ | 2 + | M2Q | 2 .
O
x
y
z
M 1
M 2
P
Q
d = | M1M2 | =
所以
与z 轴平行的边的边长为|z 2 z 1|.
与y 轴平行的边的边长为|y 2 y 1|,
设M 1(x 1,y 1,z 1)、M 2(x 2,y 2,z 2)为空间两点.
与x 轴平行的边的边长为|x 2 x 1|,
作一个以M 1和M 2为对角线顶点的长方体,使其三个相邻的面分别平行于三个坐标面.
例1 求空间两点A(3,-2,5),
B(6,0,-1)的距离AB
分析:利用两点间距离公式可得
公式的记忆方法:同名坐标差的平方和的算术根
练1:P(1,2,-2)和Q(-1,0,-1)的距离是________
练2:给定空间直角坐标系,在x轴上找一点P,使它与点P0(4,1,2) 距离为
分析:设P(x,0,0),由已知求得x=9或-1
(9,0,0)或(-1,0,0)
3
已知A(X1,Y1,Z1),B(X2,Y2,Z2),则AB的中点坐标是(X,Y,Z)
X=1/2· (X1+X2),Y=1/2 · (Y1+Y2),Z=1/2 · (Z1+Z2).
想一想?
例2:在xoy平面内的直线x+y=1上确定一点M,使M到N(6,5,1)的距离最小
略解:设M(x,1-x,0),利用距离公式构造出一个二次函数后求最值
例3.平面上到坐标原点的距离为1的点的轨迹是单位圆,其方程为 .
在空间中,到坐标原点的距离为1的点的轨迹是什么?试写出它的方程.
练4:如图:M—OAB是棱长为a的正四面体,顶点M在底面OAB上的射影为H,分别求出点B、H、M的坐标
M
A
H
B
O
z
x
y
小结:1、画坐标系,标点;
2 、中点坐标公式、距离公式.
作业:略
O
z
y
x
第一卦限
卦 限:
三个坐标面把
空间分成八个部分,
每一部分叫做卦限.
O
z
y
x
第二卦限
卦 限:
第三卦限
O
z
y
x
卦 限:
O
z
y
x
第四卦限
卦 限:
O
z
y
x
第五卦限
卦 限:
O
z
y
x
第六卦限
卦 限:
O
z
y
x
第七卦限
卦 限:
O
z
y
x
第八卦限
卦 限:
3.3空间两点间的距离公式
问题1:长方体的对角线是长方体中的那一条线段?
问题2:怎样测量长方体的对角线的长?
问题3:已知长方体的长、宽、高分别是a、b、c,则对角线的长
问题4:给出空间两点A(x1,y1,z1),P(x2,y2,z2)
可否类比得到一个距离公式?
1、设O(0,0,0),P(x0,y0,z0)则
x
y
z
o
P
A
B
C
O
x
y
z
设M 1(x 1,y 1,z 1)、M 2(x 2,y 2,z 2)为空间两点.
与x 轴平行的边的边长为|x 2 x 1|,
作一个以M 1和M 2为对角线顶点的长方体,使其三个相邻的面分别平行于三个坐标面.
M 1
M 2
P
Q
x 2
x 1
与y 轴平行的边的边长为|y 2 y 1|,
y 2
y 1
O
x
y
z
M 1
M 2
P
Q
设M 1(x 1,y 1,z 1)、M 2(x 2,y 2,z 2)为空间两点.
与x 轴平行的边的边长为|x 2 x 1|,
作一个以M 1和M 2为对角线顶点的长方体,使其三个相邻的面分别平行于三个坐标面.
与z 轴平行的边的边长为|z 2 z 1|.
z 2
z 1
O
x
y
z
M 1
M 2
P
Q
与y 轴平行的边的边长为|y 2 y 1|,
设M 1(x 1,y 1,z 1)、M 2(x 2,y 2,z 2)为空间两点.
与x 轴平行的边的边长为|x 2 x 1|,
作一个以M 1和M 2为对角线顶点的长方体,使其三个相邻的面分别平行于三个坐标.
因为
| M1M2 | 2
= | M1Q | 2 + | M2Q | 2
= | M1P | 2 + | PQ | 2 + | M2Q | 2 .
O
x
y
z
M 1
M 2
P
Q
d = | M1M2 | =
所以
与z 轴平行的边的边长为|z 2 z 1|.
与y 轴平行的边的边长为|y 2 y 1|,
设M 1(x 1,y 1,z 1)、M 2(x 2,y 2,z 2)为空间两点.
与x 轴平行的边的边长为|x 2 x 1|,
作一个以M 1和M 2为对角线顶点的长方体,使其三个相邻的面分别平行于三个坐标面.
例1 求空间两点A(3,-2,5),
B(6,0,-1)的距离AB
分析:利用两点间距离公式可得
公式的记忆方法:同名坐标差的平方和的算术根
练1:P(1,2,-2)和Q(-1,0,-1)的距离是________
练2:给定空间直角坐标系,在x轴上找一点P,使它与点P0(4,1,2) 距离为
分析:设P(x,0,0),由已知求得x=9或-1
(9,0,0)或(-1,0,0)
3
已知A(X1,Y1,Z1),B(X2,Y2,Z2),则AB的中点坐标是(X,Y,Z)
X=1/2· (X1+X2),Y=1/2 · (Y1+Y2),Z=1/2 · (Z1+Z2).
想一想?
例2:在xoy平面内的直线x+y=1上确定一点M,使M到N(6,5,1)的距离最小
略解:设M(x,1-x,0),利用距离公式构造出一个二次函数后求最值
例3.平面上到坐标原点的距离为1的点的轨迹是单位圆,其方程为 .
在空间中,到坐标原点的距离为1的点的轨迹是什么?试写出它的方程.
练4:如图:M—OAB是棱长为a的正四面体,顶点M在底面OAB上的射影为H,分别求出点B、H、M的坐标
M
A
H
B
O
z
x
y
小结:1、画坐标系,标点;
2 、中点坐标公式、距离公式.
作业:略
