北师大版高中数学必修2《空间直角坐标系》参考课件1(共34张PPT)
文档属性
| 名称 | 北师大版高中数学必修2《空间直角坐标系》参考课件1(共34张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 00:00:00 | ||
图片预览








文档简介
(共34张PPT)
:如何确定空中飞行的飞机的位置?
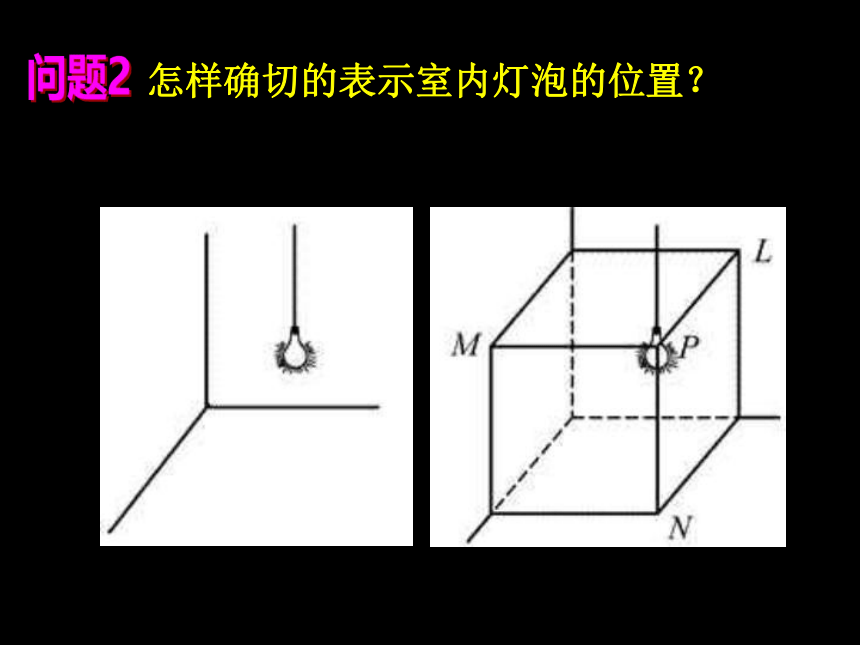
怎样确切的表示室内灯泡的位置?
对问题1,2的分析
对于直线上的点,我们可以通过建立数轴来确定点的位置;
对于平面上的点,我们可以通过建立平面直角坐标系来确定点的位置;
对于空间中的点,我们也希望建立适当的坐标系来确定点的位置.
因此,如何在空间中建立坐标系,就成为我们需要研究的课题.
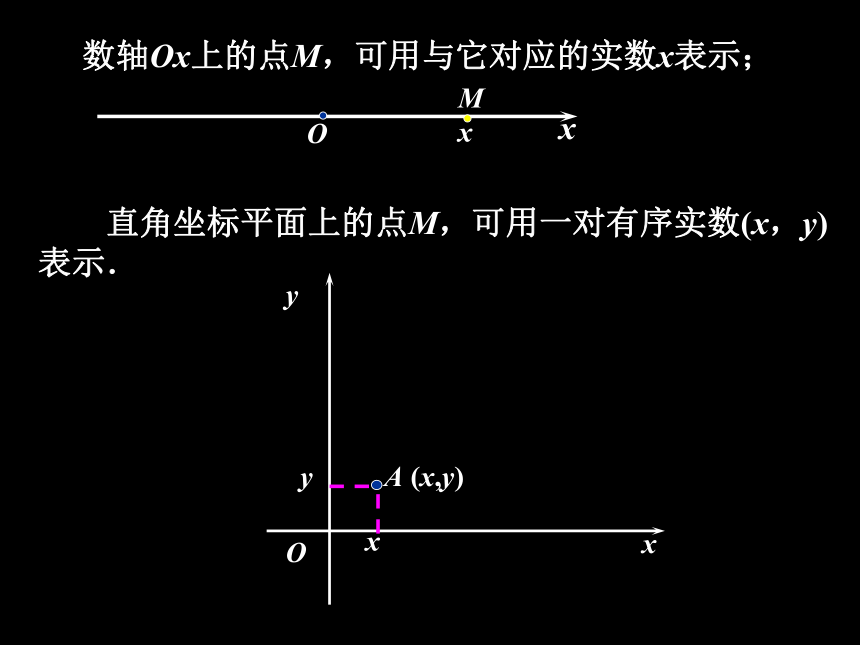
数轴Ox上的点M,可用与它对应的实数x表示;
直角坐标平面上的点M,可用一对有序实数(x,y)表示.
x
O
x
M
x
O
y
A
(x,y)
x
y
知识探究(一):空间直角坐标系
归纳:数轴上的点M的坐标用一个实数x表示,它是一维坐标;平面上的点M的坐标用一对有序实数(x,y)表示,它是二维坐标.设想:对于空间中的点M的坐标,需要几个实数表示?
O
x
x
O
x
(x,y)
y
联想并思考1:平面直角坐标系是由两条互相垂直的数轴组成,请大家想一想:怎样建立一个空间直角坐标系?空间直角坐标系由几条数轴组成呢?其相对位置关系如何?
三条交于一点且两两互相垂直的数轴
空间直角坐标系的建立:在空间中,过任意的一点O作三条两两互相垂直的具有相同长度单位的数轴:x轴、y轴、z轴,组成空间直角坐标系O-xyz,(如下图所示)其中点O叫做坐标原点,x轴、y轴、z轴叫做坐标轴,通过每两个坐标轴的平面叫做坐标平面,并分别称为xOy平面、yOz平面、xOz平面.
x
y
z
O
x
z
y
O
思考2:在空间直角坐标系Oxyz中,
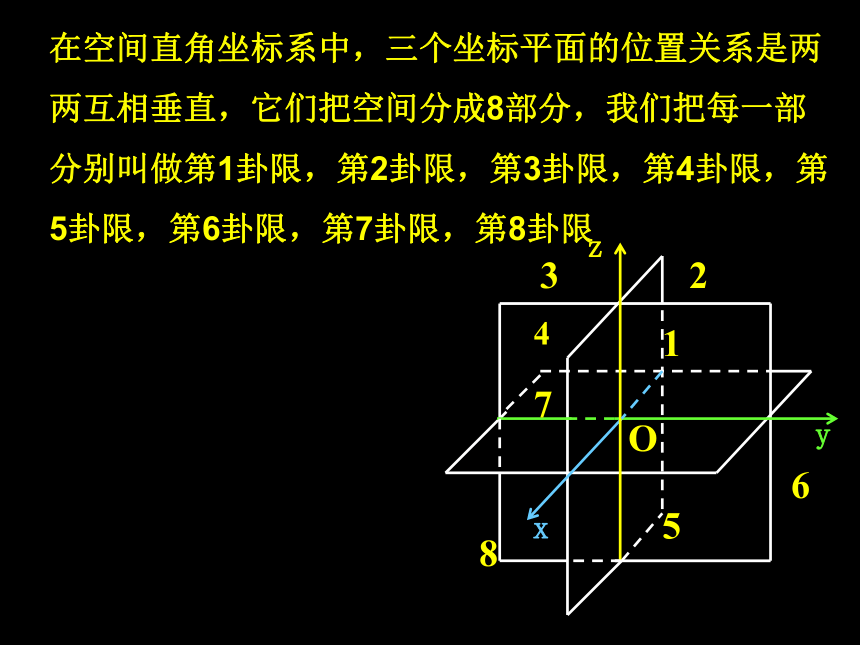
三个坐标平面的位置关系如何?它们将空间分成几个部分?
在空间直角坐标系中,三个坐标平面的位置关系是两两互相垂直,它们把空间分成8部分,我们把每一部分别叫做第1卦限,第2卦限,第3卦限,第4卦限,第5卦限,第6卦限,第7卦限,第8卦限
x
z
y
1
2
3
4
5
6
8
7
O
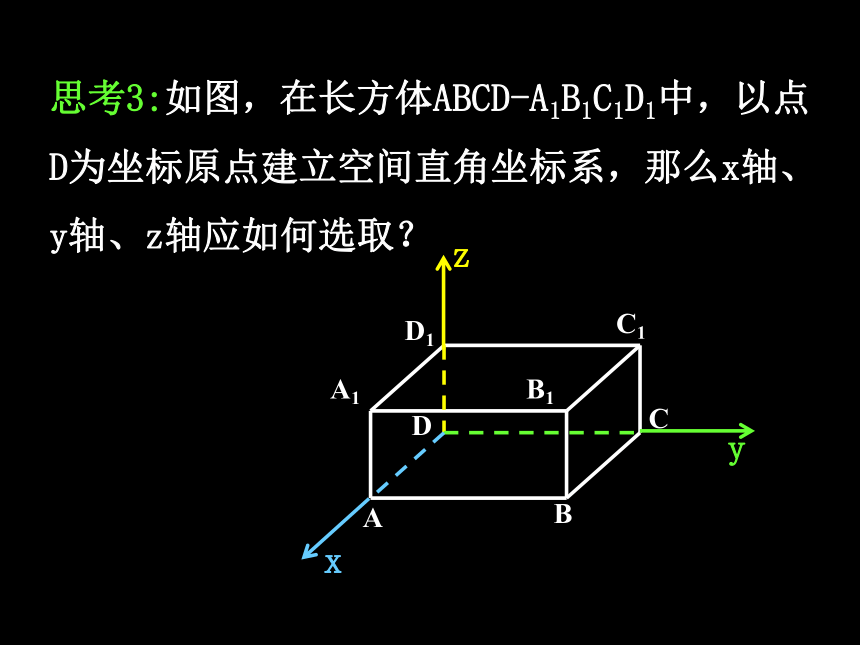
思考3:如图,在长方体ABCD-A1B1C1D1中,以点D为坐标原点建立空间直角坐标系,那么x轴、y轴、z轴应如何选取?
A
B
C
D
A1
B1
C1
D1
x
y
z
知识探究(二)空间直角坐标系中点的坐标
思考1:在平面直角坐标系中,点M的横坐标、纵坐标的含义如何?
O
x
(x,y)
y
|x|
|y|
思考:在空间直角坐标系中,怎样描述一点M位置呢?
在空间直角坐标系中,设点M为空间的一个定点,过点M分别作垂直于x轴、y轴、z轴的平面,垂足为A、B、C. 设点A、B、C在x轴、y轴、z轴上的坐标分别为x、y、z,那么点M的位置与有序实数组(x,y,z)是一个什么对应关系?
A
O
x
M
y
z
x
x
C
O
M
y
z
z
B
O
x
M
y
z
y
设点M是空间的一个定点,过点M分别作垂直于x 轴、y 轴和z 轴的平面,依次交x 轴、y 轴和z 轴于点P、Q和R.
空间直角坐标系中点的坐标的确定方法
y
x
z
M
O
设点P、Q和R在x 轴、y 轴和z 轴上的坐标分别是x,y和z,那么点M就对应唯一确定的有序实数组(x,y,z).
M
R
Q
P
我们把有序实数组(x,y,z)称为点M的空间坐标,记为M (x,y,z)其中x、y、z分别叫做点M的横坐标、纵坐标、竖坐标。
A
B
C
O
x
M
y
z
x
y
z
点M
(X,Y,Z)
反过来,对于一个有序实数组(x,y,z),它也唯一的对应着空间直角坐标系中的点。在x 轴、y 轴和z 轴上依次取坐标为x,y和z的点P、Q, R
y
x
z
M’
O
M
R
Q
P
分别过P、Q 、 R各作一个平面,分别垂直于x 轴、y 轴和z 轴,
这三个平面的唯一交点就是有序实数组(x,y,z)确定的点M.
例如在空间直角坐标系中怎样求点M(1,2,3)的位置呢?
方法一:分析:因为点P在第一卦限,故在x轴上取点P(1,0,0),在y轴上取点 Q(0,2,0),在z轴上取点R(0,0,3)然后过A,B,C分别作x轴,y轴, z轴的垂面,则这三个垂面的交点就是点P如图所示:
方法二:先画一个长方体使共顶点的三条棱长分别为1,2,3
M
O
R
Q
x
y
M
P
z
思考2:设点M的坐标为(a,b,c)过点M分别作xOy平面、yOz平面、xOz平面的垂线,那么三个垂足的坐标分别如何?
A
B
C
O
x
M
y
z
A(a,b,0)
B(0,b,c)
C(a,0,c)
思考2:x轴、y轴、z轴上的点的坐标有何特点?xOy平面、yOz平面、xOz平面上的点的坐标有何特点?
x轴上的点:(x,0,0)
xOy平面上的点:(x,y,0)
x
y
z
O
xoy平面上的点竖坐标为0 例如:D点坐标记为D(a,b,0)
yoz平面上的点横坐标为0 例如:E点坐标记为E(0,b,c)
xoz平面上的点纵坐标为0 例如:F点坐标记为F(a,0,c)
x轴上的点纵坐标竖坐为0. 例如:A点坐标记为A(a,0,0)
z轴上的点横坐标纵坐标为0.例如:C点坐标记为C(0,0,c)
y轴上的点横坐标竖坐标为0.例如:B点坐标记为B(0,b,0)
二、坐标平面内的点
一、坐标轴上的点
A
B
C
O
x
M
y
z
D
E
F
思考3:在空间直角坐标系中,在每个卦限内点的横,纵,竖坐标的符号分别具有怎样的特点?
x
z
y
1
2
3
4
5
6
8
7
O
(1)点M (x,y,z)在第1卦限时,则X>0,y>0,z>o,
(2)点M (x,y,z)在第2卦限则,X<0,y>0,z>o,
(3)点M (x,y,z)在第3卦限时,则X<0,y<0,z>o,
(4)点M (x,y,z)在第4卦限时,则X>0,y<0,z>o,
x
z
y
1
2
3
4
5
6
8
7
O
(5)点M (x,y,z)在第5卦限时,则X>0,y>0,z(6)点M (x,y,z)在第6卦限时,则X<0,y>0,z(7)点M (x,y,z)在第7卦限时,则X<0,y<0,z(8)点M (x,y,z)在第8卦限时,则X>0,y<0,zx
z
y
1
2
3
4
5
6
8
7
O
思考3:设点M的坐标为(x,y,z)那么点M关于x轴、y轴、z轴及原点对称的点的坐标分别是什么?
x
y
z
O
M(x,y,z)
N(x,-y,-z)
点M(x,y,z)是空间直角坐标系中的一点,则有
(1)与M点关于X轴对称的点为 (x,-y,-z)
(2)与M点关于Y轴对称的点为 (-x,y,-z)
(3)与M点关于Z轴对称的点 为(-x,-y,z)
(4)与M点关于原点对称的点 为(-x,-y,-z)
(5)与M点关于xoy平面对称的点为 (x,y,-z)
(6)与M点关于yoz平面对称的点 为(-x,y,z)
(7)与M点关于xoz平面对称的点 为(x,-y,z)
思考4:设点A(x1,y1,z1),点 B(x2,y2,z2),则线段AB的中点M的坐标如何?
y
x
z
A
B
C
O
例1:OABC—A’B’C’D’是单位正方体.以O为原点分别以射线OA,OC, OD’的方向为正方向,以线段OA,OC, OD’的长为单位长,建立空间直角坐标系O—xyz.试说出正方体的各个顶点的坐标.并指出哪些点在坐标轴上,哪些点在坐标平面上.
(0,0,0)
(1,0,0)
(1,1,0)
(0,1,0)
(1,0,1)
(1,1,1)
(0,1,1)
(0,0,1)
例2 、在长方体OABC-D′A′B′C′中,已知|OA|=3,|OC|=4, |OD′|=2,建立如图所示的空间直角坐标系,试写出长方体各顶点的坐标.
A
B
C
O
x
A′
y
z
B′
C′
D′
例3、如下图,在长方体OABC-D`A`B`C`中,|OA|=3,|OC|=4,|OD`|=3,A`C`于B`D`相交于点P.分别写出点C,B`,P的坐标.
z
x
y
O
A
C
D`
B
A`
B`
C`
P
P`
z
y
A
B
C
O
A`
D`
C`
B`
Q
Q`
例4、如图,棱长为a的正方体OABC-D`A`B`C`中,对角线OB`于BD`相交于点Q.顶点O为坐标原点,OA,OC分别在x轴、y轴的正半轴上.试写出点Q的坐标.
x
z
x
y
O
例5、在空间直角坐标系中标出下列各点:
A(0,2,4) B(1,0,5) C(0,2,0) D(1,3,4)
1
3
4
D`
D
解:把图中的钠原子分成上、中、下三层来写它们所在位置的坐标.
例5, 结晶体的基本单位称为晶胞,如图是食盐晶胞的示意图(可看成是八个棱长为 1 的小正方体堆积成的正方体),其中色点代表钠原子,黑点代表氯原子.
如图建立空间直角坐标系O-xyz后,试写出全部钠原子所在位置的坐标.
x
y
z
O
上层的原子所在的平面平行于平面,与轴交点的竖坐标为1,所以,这五个钠原子所在位置的坐标分别是:
(0,0,1),(1,0,1),(1,1,1),(0,1,1),
( , ,1).
中层的原子所在的平面平行于平面,与轴交点的竖坐标为,所以,这四个钠原子所在位置的坐标分别是
( ,0, ),(1, , ),( ,1, ),(0, , );
下层的原子全部在平面上,它们所在位置的竖坐标全是0,所以这五个钠原子所在位置的坐标分别是(0,0,0),(1,0,0),(1,1,0),(0,1,0),
( , ,0).
x
y
z
O
思考:若建立如图所示空间直角坐标系那么全部钠原子所在位置的坐标不变吗
x
y
z
O
O
:如何确定空中飞行的飞机的位置?
怎样确切的表示室内灯泡的位置?
对问题1,2的分析
对于直线上的点,我们可以通过建立数轴来确定点的位置;
对于平面上的点,我们可以通过建立平面直角坐标系来确定点的位置;
对于空间中的点,我们也希望建立适当的坐标系来确定点的位置.
因此,如何在空间中建立坐标系,就成为我们需要研究的课题.
数轴Ox上的点M,可用与它对应的实数x表示;
直角坐标平面上的点M,可用一对有序实数(x,y)表示.
x
O
x
M
x
O
y
A
(x,y)
x
y
知识探究(一):空间直角坐标系
归纳:数轴上的点M的坐标用一个实数x表示,它是一维坐标;平面上的点M的坐标用一对有序实数(x,y)表示,它是二维坐标.设想:对于空间中的点M的坐标,需要几个实数表示?
O
x
x
O
x
(x,y)
y
联想并思考1:平面直角坐标系是由两条互相垂直的数轴组成,请大家想一想:怎样建立一个空间直角坐标系?空间直角坐标系由几条数轴组成呢?其相对位置关系如何?
三条交于一点且两两互相垂直的数轴
空间直角坐标系的建立:在空间中,过任意的一点O作三条两两互相垂直的具有相同长度单位的数轴:x轴、y轴、z轴,组成空间直角坐标系O-xyz,(如下图所示)其中点O叫做坐标原点,x轴、y轴、z轴叫做坐标轴,通过每两个坐标轴的平面叫做坐标平面,并分别称为xOy平面、yOz平面、xOz平面.
x
y
z
O
x
z
y
O
思考2:在空间直角坐标系Oxyz中,
三个坐标平面的位置关系如何?它们将空间分成几个部分?
在空间直角坐标系中,三个坐标平面的位置关系是两两互相垂直,它们把空间分成8部分,我们把每一部分别叫做第1卦限,第2卦限,第3卦限,第4卦限,第5卦限,第6卦限,第7卦限,第8卦限
x
z
y
1
2
3
4
5
6
8
7
O
思考3:如图,在长方体ABCD-A1B1C1D1中,以点D为坐标原点建立空间直角坐标系,那么x轴、y轴、z轴应如何选取?
A
B
C
D
A1
B1
C1
D1
x
y
z
知识探究(二)空间直角坐标系中点的坐标
思考1:在平面直角坐标系中,点M的横坐标、纵坐标的含义如何?
O
x
(x,y)
y
|x|
|y|
思考:在空间直角坐标系中,怎样描述一点M位置呢?
在空间直角坐标系中,设点M为空间的一个定点,过点M分别作垂直于x轴、y轴、z轴的平面,垂足为A、B、C. 设点A、B、C在x轴、y轴、z轴上的坐标分别为x、y、z,那么点M的位置与有序实数组(x,y,z)是一个什么对应关系?
A
O
x
M
y
z
x
x
C
O
M
y
z
z
B
O
x
M
y
z
y
设点M是空间的一个定点,过点M分别作垂直于x 轴、y 轴和z 轴的平面,依次交x 轴、y 轴和z 轴于点P、Q和R.
空间直角坐标系中点的坐标的确定方法
y
x
z
M
O
设点P、Q和R在x 轴、y 轴和z 轴上的坐标分别是x,y和z,那么点M就对应唯一确定的有序实数组(x,y,z).
M
R
Q
P
我们把有序实数组(x,y,z)称为点M的空间坐标,记为M (x,y,z)其中x、y、z分别叫做点M的横坐标、纵坐标、竖坐标。
A
B
C
O
x
M
y
z
x
y
z
点M
(X,Y,Z)
反过来,对于一个有序实数组(x,y,z),它也唯一的对应着空间直角坐标系中的点。在x 轴、y 轴和z 轴上依次取坐标为x,y和z的点P、Q, R
y
x
z
M’
O
M
R
Q
P
分别过P、Q 、 R各作一个平面,分别垂直于x 轴、y 轴和z 轴,
这三个平面的唯一交点就是有序实数组(x,y,z)确定的点M.
例如在空间直角坐标系中怎样求点M(1,2,3)的位置呢?
方法一:分析:因为点P在第一卦限,故在x轴上取点P(1,0,0),在y轴上取点 Q(0,2,0),在z轴上取点R(0,0,3)然后过A,B,C分别作x轴,y轴, z轴的垂面,则这三个垂面的交点就是点P如图所示:
方法二:先画一个长方体使共顶点的三条棱长分别为1,2,3
M
O
R
Q
x
y
M
P
z
思考2:设点M的坐标为(a,b,c)过点M分别作xOy平面、yOz平面、xOz平面的垂线,那么三个垂足的坐标分别如何?
A
B
C
O
x
M
y
z
A(a,b,0)
B(0,b,c)
C(a,0,c)
思考2:x轴、y轴、z轴上的点的坐标有何特点?xOy平面、yOz平面、xOz平面上的点的坐标有何特点?
x轴上的点:(x,0,0)
xOy平面上的点:(x,y,0)
x
y
z
O
xoy平面上的点竖坐标为0 例如:D点坐标记为D(a,b,0)
yoz平面上的点横坐标为0 例如:E点坐标记为E(0,b,c)
xoz平面上的点纵坐标为0 例如:F点坐标记为F(a,0,c)
x轴上的点纵坐标竖坐为0. 例如:A点坐标记为A(a,0,0)
z轴上的点横坐标纵坐标为0.例如:C点坐标记为C(0,0,c)
y轴上的点横坐标竖坐标为0.例如:B点坐标记为B(0,b,0)
二、坐标平面内的点
一、坐标轴上的点
A
B
C
O
x
M
y
z
D
E
F
思考3:在空间直角坐标系中,在每个卦限内点的横,纵,竖坐标的符号分别具有怎样的特点?
x
z
y
1
2
3
4
5
6
8
7
O
(1)点M (x,y,z)在第1卦限时,则X>0,y>0,z>o,
(2)点M (x,y,z)在第2卦限则,X<0,y>0,z>o,
(3)点M (x,y,z)在第3卦限时,则X<0,y<0,z>o,
(4)点M (x,y,z)在第4卦限时,则X>0,y<0,z>o,
x
z
y
1
2
3
4
5
6
8
7
O
(5)点M (x,y,z)在第5卦限时,则X>0,y>0,z
z
y
1
2
3
4
5
6
8
7
O
思考3:设点M的坐标为(x,y,z)那么点M关于x轴、y轴、z轴及原点对称的点的坐标分别是什么?
x
y
z
O
M(x,y,z)
N(x,-y,-z)
点M(x,y,z)是空间直角坐标系中的一点,则有
(1)与M点关于X轴对称的点为 (x,-y,-z)
(2)与M点关于Y轴对称的点为 (-x,y,-z)
(3)与M点关于Z轴对称的点 为(-x,-y,z)
(4)与M点关于原点对称的点 为(-x,-y,-z)
(5)与M点关于xoy平面对称的点为 (x,y,-z)
(6)与M点关于yoz平面对称的点 为(-x,y,z)
(7)与M点关于xoz平面对称的点 为(x,-y,z)
思考4:设点A(x1,y1,z1),点 B(x2,y2,z2),则线段AB的中点M的坐标如何?
y
x
z
A
B
C
O
例1:OABC—A’B’C’D’是单位正方体.以O为原点分别以射线OA,OC, OD’的方向为正方向,以线段OA,OC, OD’的长为单位长,建立空间直角坐标系O—xyz.试说出正方体的各个顶点的坐标.并指出哪些点在坐标轴上,哪些点在坐标平面上.
(0,0,0)
(1,0,0)
(1,1,0)
(0,1,0)
(1,0,1)
(1,1,1)
(0,1,1)
(0,0,1)
例2 、在长方体OABC-D′A′B′C′中,已知|OA|=3,|OC|=4, |OD′|=2,建立如图所示的空间直角坐标系,试写出长方体各顶点的坐标.
A
B
C
O
x
A′
y
z
B′
C′
D′
例3、如下图,在长方体OABC-D`A`B`C`中,|OA|=3,|OC|=4,|OD`|=3,A`C`于B`D`相交于点P.分别写出点C,B`,P的坐标.
z
x
y
O
A
C
D`
B
A`
B`
C`
P
P`
z
y
A
B
C
O
A`
D`
C`
B`
Q
Q`
例4、如图,棱长为a的正方体OABC-D`A`B`C`中,对角线OB`于BD`相交于点Q.顶点O为坐标原点,OA,OC分别在x轴、y轴的正半轴上.试写出点Q的坐标.
x
z
x
y
O
例5、在空间直角坐标系中标出下列各点:
A(0,2,4) B(1,0,5) C(0,2,0) D(1,3,4)
1
3
4
D`
D
解:把图中的钠原子分成上、中、下三层来写它们所在位置的坐标.
例5, 结晶体的基本单位称为晶胞,如图是食盐晶胞的示意图(可看成是八个棱长为 1 的小正方体堆积成的正方体),其中色点代表钠原子,黑点代表氯原子.
如图建立空间直角坐标系O-xyz后,试写出全部钠原子所在位置的坐标.
x
y
z
O
上层的原子所在的平面平行于平面,与轴交点的竖坐标为1,所以,这五个钠原子所在位置的坐标分别是:
(0,0,1),(1,0,1),(1,1,1),(0,1,1),
( , ,1).
中层的原子所在的平面平行于平面,与轴交点的竖坐标为,所以,这四个钠原子所在位置的坐标分别是
( ,0, ),(1, , ),( ,1, ),(0, , );
下层的原子全部在平面上,它们所在位置的竖坐标全是0,所以这五个钠原子所在位置的坐标分别是(0,0,0),(1,0,0),(1,1,0),(0,1,0),
( , ,0).
x
y
z
O
思考:若建立如图所示空间直角坐标系那么全部钠原子所在位置的坐标不变吗
x
y
z
O
O
