2020-2021学年人教版九年级数学下册27.2相似三角形优生辅导训练(Word版,附答案解析)
文档属性
| 名称 | 2020-2021学年人教版九年级数学下册27.2相似三角形优生辅导训练(Word版,附答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 309.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 23:37:33 | ||
图片预览



文档简介
2021-2022学年人教版九年级数学下册《27.2相似三角形》优生辅导训练(附答案)
1.如图,E是 ABCD的边BC的延长线上一点,连接AE交CD于F,则图中共有相似三角形( )
A.4对 B.3对 C.2对 D.1对
2.如图,Rt△AOB∽Rt△DOC,∠ABO=30°,∠AOB=∠COD=90°,M为OA的中点,OA=6,将△COD绕点O旋转一周,直线AD,CB交于点P,连接MP,则MP的最小值是( )
A.6﹣3 B.6﹣6 C.3 D.
3.两个相似多边形的相似比是2:3,则这两个多边形的周长比是( )
A.4:9 B. C.2:5 D.2:3
4.若两个相似三角形的对应中线的比为3:4,则它们对应角平分线的比是( )
A.1:16 B.16:9 C.4:3 D.3:4
5.如图,△ABC中,EF∥BC,=,EF=3,则BC的值为( )
A.4 B.6 C.8 D.9
6.如图,在△ABC中,AB=AC=,BC=2.现分别任作△ABC的内接矩形P1Q1M1N1,P2Q2M2N2,P3Q3M3N3,设这三个内接矩形的周长分别为c1、c2,c3,则c1+c2+c3的值是( )
A.6 B. C.12 D.
7.如图,点D,E分别在△ABC的AB,AC边上,增加下列哪些条件,①∠AED=∠B②=③=,使△ADE与△ACB一定相似( )
A.①② B.② C.①③ D.①②③
8.如图,在正方形ABCD的外侧作等边△ADE,连接BE交AC于点F,交AD于点H,连接DF并延长交AB于点G,下列结论中,正确的个数是( )
①∠CFD=60°②S△BGF=S△DHF③△AHE≌△FGB④△EDH∽△EFD.
A.4 B.3 C.2 D.1
9.如图,△ABC中,∠C=90°,BC=8m,AB=10m,点P从B点出发,沿BC方向以2m/s的速度移动,点Q从C出发,沿CA方向以1m/s的速度移动,任意一点先到达终点即停止运动.若P、Q同时分别从B、C出发,经过 秒,△CPQ∽△CBA.
10.把一个正多边形的边长放大到原来的3倍,则原图形与新图形的面积比为 .
11.如图,已知△ABC是面积为的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则点D到线段AB的距离等于(结果保留根号) .
12.如果两个相似三角形的周长比为4:9,那么它们的面积比是 .
13.如图,在 ABCD中,AF、BE分别平分∠DAB、∠ABC,点G是AF、BE的交点,AB=5,BC=3,则S△EFG:S△ABG= .
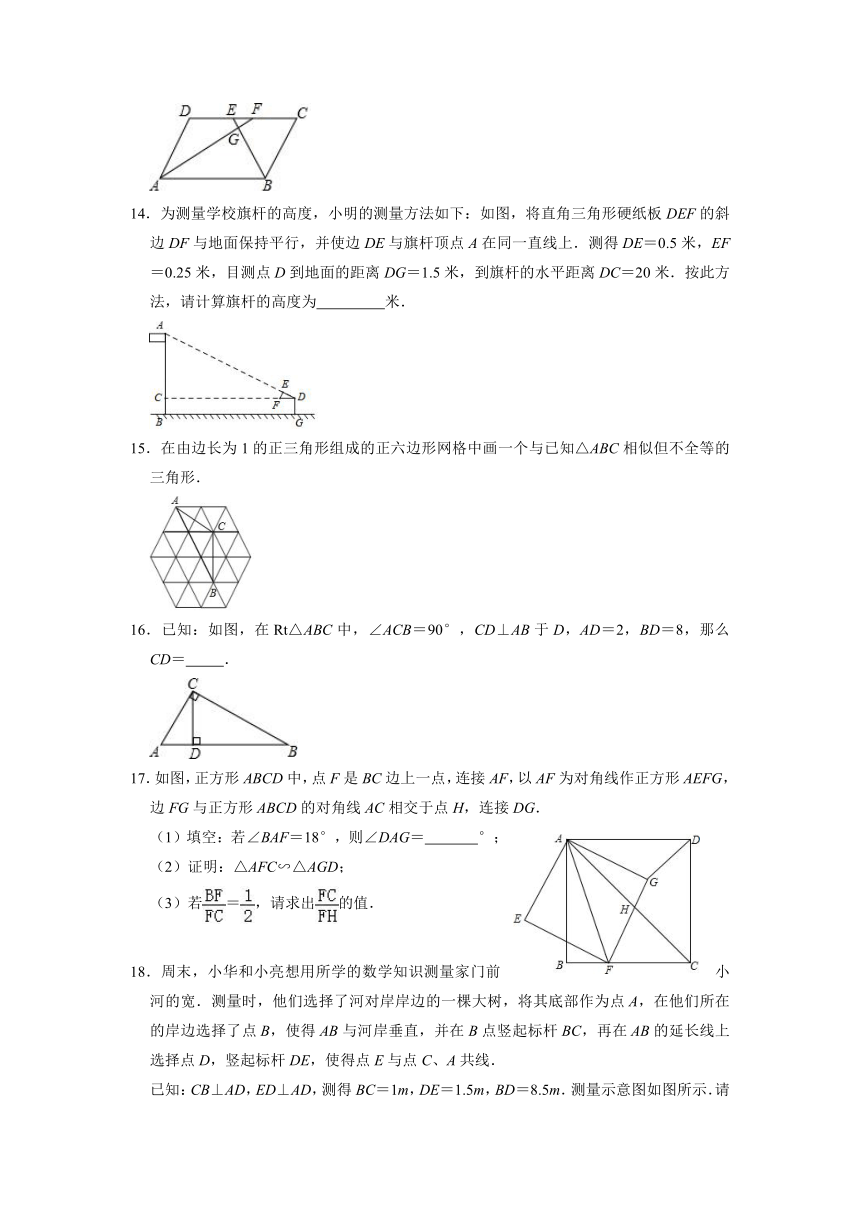
14.为测量学校旗杆的高度,小明的测量方法如下:如图,将直角三角形硬纸板DEF的斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上.测得DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米.按此方法,请计算旗杆的高度为 米.
15.在由边长为1的正三角形组成的正六边形网格中画一个与已知△ABC相似但不全等的三角形.
16.已知:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AD=2,BD=8,那么CD= .
17.如图,正方形ABCD中,点F是BC边上一点,连接AF,以AF为对角线作正方形AEFG,边FG与正方形ABCD的对角线AC相交于点H,连接DG.
(1)填空:若∠BAF=18°,则∠DAG= °;
(2)证明:△AFC∽△AGD;
(3)若=,请求出的值.
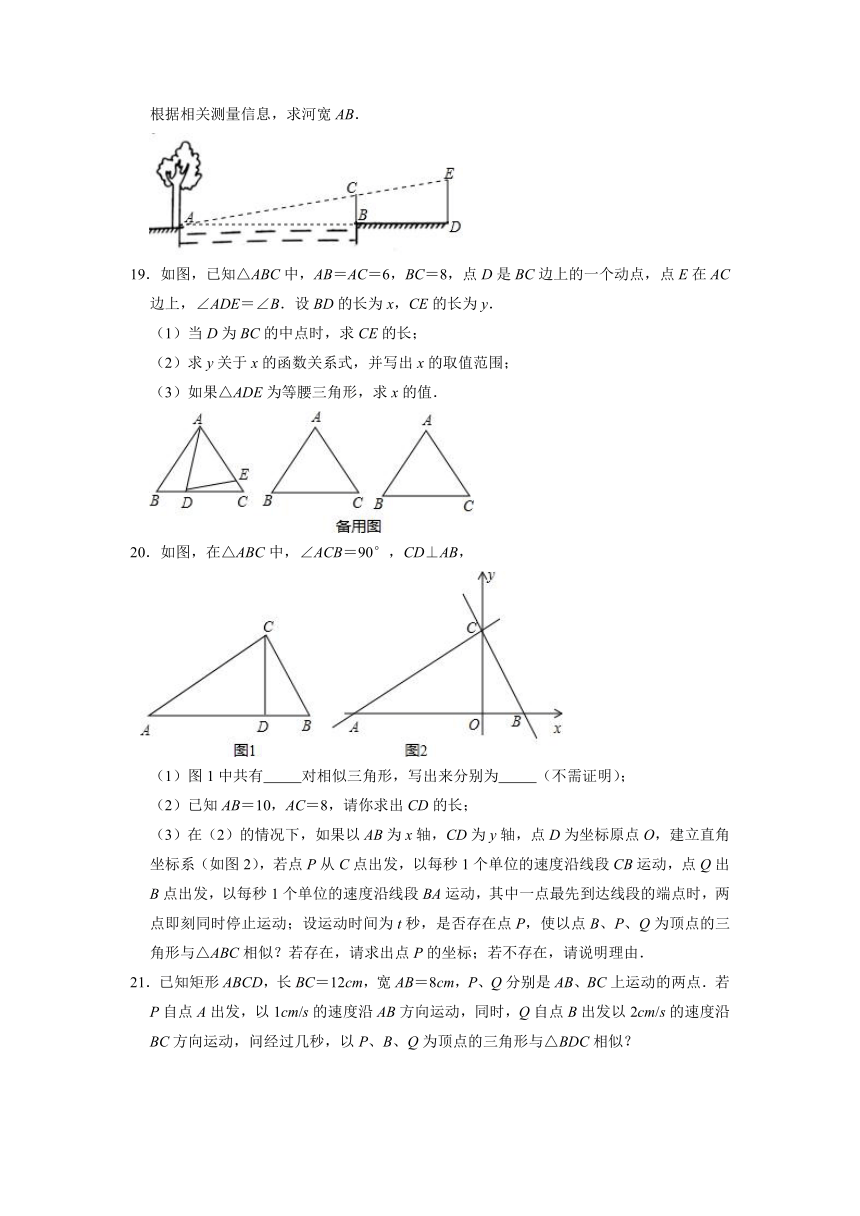
18.周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
19.如图,已知△ABC中,AB=AC=6,BC=8,点D是BC边上的一个动点,点E在AC边上,∠ADE=∠B.设BD的长为x,CE的长为y.
(1)当D为BC的中点时,求CE的长;
(2)求y关于x的函数关系式,并写出x的取值范围;
(3)如果△ADE为等腰三角形,求x的值.
如图,在△ABC中,∠ACB=90°,CD⊥AB,
(1)图1中共有 对相似三角形,写出来分别为 (不需证明);
(2)已知AB=10,AC=8,请你求出CD的长;
(3)在(2)的情况下,如果以AB为x轴,CD为y轴,点D为坐标原点O,建立直角坐标系(如图2),若点P从C点出发,以每秒1个单位的速度沿线段CB运动,点Q出B点出发,以每秒1个单位的速度沿线段BA运动,其中一点最先到达线段的端点时,两点即刻同时停止运动;设运动时间为t秒,是否存在点P,使以点B、P、Q为顶点的三角形与△ABC相似?若存在,请求出点P的坐标;若不存在,请说明理由.
21.已知矩形ABCD,长BC=12cm,宽AB=8cm,P、Q分别是AB、BC上运动的两点.若P自点A出发,以1cm/s的速度沿AB方向运动,同时,Q自点B出发以2cm/s的速度沿BC方向运动,问经过几秒,以P、B、Q为顶点的三角形与△BDC相似?
参考答案
1.解:∵ABCD是平行四边形
∴AD∥BC,DC∥AB
∴△ADF∽△EBA∽△ECF
则图中共有相似三角形有三对,
故选:B.
2.解:取AB的中点S,连接MS、PS,
则PS﹣MS≤PM≤MS+PS,
∵∠AOB=90°,OA=6,∠ABO=30°,
∴AB=2OA=12,OB=6
∵∠AOB=∠COD=90°,
∴∠COB=∠DOA,
∵△AOB∽△DOC,
∴=,
∴△COB∽△DOA,
∴∠OBC=∠OAD,
∵∠OBC+∠PBO=180°,
∴∠OAD+∠PBO=180°,∠AOB+∠APB=180°,
∴∠APB=∠AOB=90°,又S是AB的中点,
∴PS=AB=6,
∵M为OA的中点,S是AB的中点,
∴MS=OB=3,
∴MP的最小值为6﹣3,
故选:A.
3.解:∵两个相似多边形的相似比是2:3,
∴这两个多边形的周长为2:3.
故选:D.
4.解:∵两个相似三角形对应中线的比是3:4,
∴这两个相似三角形的相似比是3:4,
那么它们的对应角平分线的比为3:4,
故选:D.
5.解:∵EF∥BC,
∴△AEF∽△ABC,
∴=,
∵=,
∴=,
∵EF=3.
∴BC=9,
故选:D.
6.解:过点A作AD⊥BC于D,
∵AB=AC=,BC=2,
∴BD=CD=BC=1,∠B=∠C,
∴AD==2,
∵四边形P1Q1M1N1是矩形,
∴P1Q1=M1N1,N1P1=M1Q1,N1P1⊥BC,
∴N1P1∥AD,
∴△BN1P1∽△BAD,
∴BP1:BD=N1P1:AD,
∴N1P1=2BP1,
在△BP1N1和△CQ1M1中,
∵,
∴△BP1N1≌△CQ1M1(AAS),
∴BP1=CQ1,
∴c1=N1P1+P1Q1+M1Q1+M1N1=2BP1+2P1Q1+2BP1=2(BP1+P1Q1+BP1)=2(BP1+P1Q1+CQ1)=2BC=2×2=4,
同理:c2=c3=c1=4.
∴c1+c2+c3=12.
故选:C.
7.解:∵∠A=∠A,∠AED=∠B,
∴△AED∽△ABC,故①正确,
∵∠A=∠A,=,
∴△AED∽△ABC,故③正确,
由②无法判定△ADE与△ACB相似,
故选:C.
8.解:∵四边形ABCD是正方形,
∴AB=AD=BC=CD,∠BAD=90°,∠BCF=∠DCF=∠BAC=45°,
∵△ADE是等边三角形,
∴AE=AD=DE=AB,∠DAE=60°,
∴∠BAE=150°,∵AB=AE,
∴∠ABE=∠AEB=15°,
∴∠CFB=∠FBA+∠BAF=60°,
在△FCB和△FCD中,
,
∴△FCB≌△FCD,
∴∠CFD=∠CFB=60°.故①正确,
同理可证△AFB≌△AFD,△AFG≌△AFH,
∴S△AFB=S△AFD,S△AFG=S△AFH,
∴S△BFG=S△DFH,故②正确,
在△BFG中的最长边BF,△AHE中的最长边为AE,显然BF<AE,
∴△AHE与△FGB 不全等,故③错误,
∵∠AFE=∠BFC=∠CFD=60°,
∴∠DFE=60°=∠EDH,∵∠DEH=∠FED,
∴△EDH∽△EFD,故④正确.
故选:B.
9.解:设经过t秒时,△CPQ∽△CBA,
∵如图,△ABC中,∠C=90°,BC=8m,AB=10m,
∴由勾股定理求得:AC===6(m).
∵△CPQ∽△CBA,
∴CP:CB=CQ:CA,即(8﹣2t):8=t:6.
∴t=2.4.
故答案是:2.4.
10.解:把一个正多边形的边长放大到原来的3倍,
则原图形与新图形的相似比为1:3,
∴原图形与新图形的面积比为1:9,
故答案为:1:9.
11.解:∵△ABC∽△ADE,AB=2AD,
∴=()2=4,
∵S△ABC=,
∴S△ADE=,
∵△ABC是等边三角形,△ABC∽△ADE,
∴△ADE是等边三角形,
∴AD2=,
∴AD=1.
如图,过点D作DH⊥AB于H.
在△ADH中,∵∠HAD=45°,
∴DH=AD sin∠HAD=1×=.
故答案为.
12.解:∵两个相似三角形的周长比为4:9,
∴两个相似三角形的相似比为4:9,
∴两个相似三角形的面积比为16:81,
故答案为:16:81.
13.解:
∵BE分别平分ABC
∴∠ABE=∠EBC
∵在 ABCD中,DC∥AB
∴∠ABE=∠EBC=∠BEC
∴CE=BC=3
同理可得∠DAF=∠DFA,AD=DF=3
∵在 ABCD中,AB=DC=5
∴EF=1
∵在△EFG和△ABG中,
∴△EFG∽△ABG
∴==
故答案为:1:25
14.解:由题意得:∠DEF=∠DCA=90°,∠EDF=∠CDA,
∴△DEF∽△DCA,
则=,即=,
解得:AC=10,
故AB=AC+BC=10+1.5=11.5(米),
即旗杆的高度为11.5米;
故答案为:11.5.
15.解:如图所示,△A′BC即为所求.
16.解:∵∠ACB=90°,CD⊥AB,
∴CD2=AD BD=16,
则CD=4,
故答案为:4.
17.解:(1)∵四边形ABCD,AEFG是正方形,
∴∠BAC=∠GAF=45°,
∴∠BAF+∠FAC=∠FAC+∠GAC=45°,
∴∠HAG=∠BAF=18°,
∵∠DAG+∠GAH=∠DAC=45°,
∴∠DAG=45°﹣18°=27°,
故答案为:27.
(2)∵四边形ABCD,AEFG是正方形,
∴=,=,
∴=,
∵∠DAG+∠GAC=∠FAC+∠GAC=45°,
∴∠DAG=∠CAF,
∴△AFC∽△AGD;
(3)∵=,
设BF=k,CF=2k,则AB=BC=3k,
∴AF===k,AC=AB=3k,
∵四边形ABCD,AEFG是正方形,
∴∠AFH=∠ACF,∠FAH=∠CAF,
∴△AFH∽△ACF,
∴=,
∴==.
18.解:∵BC∥DE,
∴△ABC∽△ADE,
∴=,
∴=,
∴AB=17(m),
经检验:AB=17是分式方程的解,
答:河宽AB的长为17米.
19.解:(1)∵AB=AC,
∴∠B=∠C,
∵∠ADC=∠ADE+∠CDE=∠B+∠BAD,
而∠ADE=∠B,
∴∠BAD=∠CDE,
∴△ABD∽△DCE,
∴=,=,
∴y=﹣x2+x,
当x=4时,y=﹣×16+×4=,
即当D为BC的中点时,CE的长为;
(2)由(1)得y关于x的函数关系式为y=﹣x2+x(0≤x<8);
(3)∵∠AED>∠C,
而∠B=∠ADE=∠C,
∴∠AED>∠ADE,
∴AE<AD,
当DA=DE时,
∵△ABD∽△DCE,
∴=,即=1,
∴x=y,
∴﹣x2+x=x,解得x1=0,x2=2,
当EA=ED时,则∠EAD=∠ADE,
而∠ADE=∠C,
∴∠EAD=∠C,
∴△DAC∽△ABC,
∴=,即=,
∴x=,
综上所述,当△ADE为等腰三角形,x的值为0或2或.
20.解:(1)图1中共有3对相似三角形,分别为:△ABC∽△ACD,△ABC∽△CBD,△ACD∽△CBD.
故答案为3,△ABC∽△ACD,△ABC∽△CBD,△ACD∽△CBD;
(2)如图1,在△ABC中,∵∠ACB=90°,AB=10,AC=8,
∴BC==6.
∵△ABC的面积=AB CD=AC BC,
∴CD===4.8;
(3)存在点P,使以点B、P、Q为顶点的三角形与△ABC相似,理由如下:
在△BOC中,∵∠COB=90°,BC=6,OC=4.8,
∴OB==3.6.
分两种情况:
①当∠BQP=90°时,如图2①,此时△PQB∽△ACB,
∴=,
∴=,
解得t=2.25,即BQ=CP=2.25,
∴BP=BC﹣CP=6﹣2.25=3.75.
在△BPQ中,由勾股定理,得PQ===3,
∴点P的坐标为(1.35,3);
②当∠BPQ=90°时,如图2②,此时△QPB∽△ACB,
∴=,
∴=,
解得t=3.75,即BQ=CP=3.75,BP=BC﹣CP=6﹣3.75=2.25.
过点P作PE⊥x轴于点E.
∵△QPB∽△ACB,
∴=,即=,
∴PE=1.8.
在△BPE中,BE===1.35,
∴OE=OB﹣BE=3.6﹣1.35=2.25,
∴点P的坐标为(2.25,1.8).
综上可得,点P的坐标为(1.35,3)或(2.25,1.8).
21.解:设经x秒后,△PBQ∽△BCD,
由于∠PBQ=∠BCD=90°,
(1)当∠1=∠2时,有:,
即;
(2)当∠1=∠3时,有:,
即,
∴经过秒或2秒,△PBQ∽△BCD.
1.如图,E是 ABCD的边BC的延长线上一点,连接AE交CD于F,则图中共有相似三角形( )
A.4对 B.3对 C.2对 D.1对
2.如图,Rt△AOB∽Rt△DOC,∠ABO=30°,∠AOB=∠COD=90°,M为OA的中点,OA=6,将△COD绕点O旋转一周,直线AD,CB交于点P,连接MP,则MP的最小值是( )
A.6﹣3 B.6﹣6 C.3 D.
3.两个相似多边形的相似比是2:3,则这两个多边形的周长比是( )
A.4:9 B. C.2:5 D.2:3
4.若两个相似三角形的对应中线的比为3:4,则它们对应角平分线的比是( )
A.1:16 B.16:9 C.4:3 D.3:4
5.如图,△ABC中,EF∥BC,=,EF=3,则BC的值为( )
A.4 B.6 C.8 D.9
6.如图,在△ABC中,AB=AC=,BC=2.现分别任作△ABC的内接矩形P1Q1M1N1,P2Q2M2N2,P3Q3M3N3,设这三个内接矩形的周长分别为c1、c2,c3,则c1+c2+c3的值是( )
A.6 B. C.12 D.
7.如图,点D,E分别在△ABC的AB,AC边上,增加下列哪些条件,①∠AED=∠B②=③=,使△ADE与△ACB一定相似( )
A.①② B.② C.①③ D.①②③
8.如图,在正方形ABCD的外侧作等边△ADE,连接BE交AC于点F,交AD于点H,连接DF并延长交AB于点G,下列结论中,正确的个数是( )
①∠CFD=60°②S△BGF=S△DHF③△AHE≌△FGB④△EDH∽△EFD.
A.4 B.3 C.2 D.1
9.如图,△ABC中,∠C=90°,BC=8m,AB=10m,点P从B点出发,沿BC方向以2m/s的速度移动,点Q从C出发,沿CA方向以1m/s的速度移动,任意一点先到达终点即停止运动.若P、Q同时分别从B、C出发,经过 秒,△CPQ∽△CBA.
10.把一个正多边形的边长放大到原来的3倍,则原图形与新图形的面积比为 .
11.如图,已知△ABC是面积为的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则点D到线段AB的距离等于(结果保留根号) .
12.如果两个相似三角形的周长比为4:9,那么它们的面积比是 .
13.如图,在 ABCD中,AF、BE分别平分∠DAB、∠ABC,点G是AF、BE的交点,AB=5,BC=3,则S△EFG:S△ABG= .
14.为测量学校旗杆的高度,小明的测量方法如下:如图,将直角三角形硬纸板DEF的斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上.测得DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米.按此方法,请计算旗杆的高度为 米.
15.在由边长为1的正三角形组成的正六边形网格中画一个与已知△ABC相似但不全等的三角形.
16.已知:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AD=2,BD=8,那么CD= .
17.如图,正方形ABCD中,点F是BC边上一点,连接AF,以AF为对角线作正方形AEFG,边FG与正方形ABCD的对角线AC相交于点H,连接DG.
(1)填空:若∠BAF=18°,则∠DAG= °;
(2)证明:△AFC∽△AGD;
(3)若=,请求出的值.
18.周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
19.如图,已知△ABC中,AB=AC=6,BC=8,点D是BC边上的一个动点,点E在AC边上,∠ADE=∠B.设BD的长为x,CE的长为y.
(1)当D为BC的中点时,求CE的长;
(2)求y关于x的函数关系式,并写出x的取值范围;
(3)如果△ADE为等腰三角形,求x的值.
如图,在△ABC中,∠ACB=90°,CD⊥AB,
(1)图1中共有 对相似三角形,写出来分别为 (不需证明);
(2)已知AB=10,AC=8,请你求出CD的长;
(3)在(2)的情况下,如果以AB为x轴,CD为y轴,点D为坐标原点O,建立直角坐标系(如图2),若点P从C点出发,以每秒1个单位的速度沿线段CB运动,点Q出B点出发,以每秒1个单位的速度沿线段BA运动,其中一点最先到达线段的端点时,两点即刻同时停止运动;设运动时间为t秒,是否存在点P,使以点B、P、Q为顶点的三角形与△ABC相似?若存在,请求出点P的坐标;若不存在,请说明理由.
21.已知矩形ABCD,长BC=12cm,宽AB=8cm,P、Q分别是AB、BC上运动的两点.若P自点A出发,以1cm/s的速度沿AB方向运动,同时,Q自点B出发以2cm/s的速度沿BC方向运动,问经过几秒,以P、B、Q为顶点的三角形与△BDC相似?
参考答案
1.解:∵ABCD是平行四边形
∴AD∥BC,DC∥AB
∴△ADF∽△EBA∽△ECF
则图中共有相似三角形有三对,
故选:B.
2.解:取AB的中点S,连接MS、PS,
则PS﹣MS≤PM≤MS+PS,
∵∠AOB=90°,OA=6,∠ABO=30°,
∴AB=2OA=12,OB=6
∵∠AOB=∠COD=90°,
∴∠COB=∠DOA,
∵△AOB∽△DOC,
∴=,
∴△COB∽△DOA,
∴∠OBC=∠OAD,
∵∠OBC+∠PBO=180°,
∴∠OAD+∠PBO=180°,∠AOB+∠APB=180°,
∴∠APB=∠AOB=90°,又S是AB的中点,
∴PS=AB=6,
∵M为OA的中点,S是AB的中点,
∴MS=OB=3,
∴MP的最小值为6﹣3,
故选:A.
3.解:∵两个相似多边形的相似比是2:3,
∴这两个多边形的周长为2:3.
故选:D.
4.解:∵两个相似三角形对应中线的比是3:4,
∴这两个相似三角形的相似比是3:4,
那么它们的对应角平分线的比为3:4,
故选:D.
5.解:∵EF∥BC,
∴△AEF∽△ABC,
∴=,
∵=,
∴=,
∵EF=3.
∴BC=9,
故选:D.
6.解:过点A作AD⊥BC于D,
∵AB=AC=,BC=2,
∴BD=CD=BC=1,∠B=∠C,
∴AD==2,
∵四边形P1Q1M1N1是矩形,
∴P1Q1=M1N1,N1P1=M1Q1,N1P1⊥BC,
∴N1P1∥AD,
∴△BN1P1∽△BAD,
∴BP1:BD=N1P1:AD,
∴N1P1=2BP1,
在△BP1N1和△CQ1M1中,
∵,
∴△BP1N1≌△CQ1M1(AAS),
∴BP1=CQ1,
∴c1=N1P1+P1Q1+M1Q1+M1N1=2BP1+2P1Q1+2BP1=2(BP1+P1Q1+BP1)=2(BP1+P1Q1+CQ1)=2BC=2×2=4,
同理:c2=c3=c1=4.
∴c1+c2+c3=12.
故选:C.
7.解:∵∠A=∠A,∠AED=∠B,
∴△AED∽△ABC,故①正确,
∵∠A=∠A,=,
∴△AED∽△ABC,故③正确,
由②无法判定△ADE与△ACB相似,
故选:C.
8.解:∵四边形ABCD是正方形,
∴AB=AD=BC=CD,∠BAD=90°,∠BCF=∠DCF=∠BAC=45°,
∵△ADE是等边三角形,
∴AE=AD=DE=AB,∠DAE=60°,
∴∠BAE=150°,∵AB=AE,
∴∠ABE=∠AEB=15°,
∴∠CFB=∠FBA+∠BAF=60°,
在△FCB和△FCD中,
,
∴△FCB≌△FCD,
∴∠CFD=∠CFB=60°.故①正确,
同理可证△AFB≌△AFD,△AFG≌△AFH,
∴S△AFB=S△AFD,S△AFG=S△AFH,
∴S△BFG=S△DFH,故②正确,
在△BFG中的最长边BF,△AHE中的最长边为AE,显然BF<AE,
∴△AHE与△FGB 不全等,故③错误,
∵∠AFE=∠BFC=∠CFD=60°,
∴∠DFE=60°=∠EDH,∵∠DEH=∠FED,
∴△EDH∽△EFD,故④正确.
故选:B.
9.解:设经过t秒时,△CPQ∽△CBA,
∵如图,△ABC中,∠C=90°,BC=8m,AB=10m,
∴由勾股定理求得:AC===6(m).
∵△CPQ∽△CBA,
∴CP:CB=CQ:CA,即(8﹣2t):8=t:6.
∴t=2.4.
故答案是:2.4.
10.解:把一个正多边形的边长放大到原来的3倍,
则原图形与新图形的相似比为1:3,
∴原图形与新图形的面积比为1:9,
故答案为:1:9.
11.解:∵△ABC∽△ADE,AB=2AD,
∴=()2=4,
∵S△ABC=,
∴S△ADE=,
∵△ABC是等边三角形,△ABC∽△ADE,
∴△ADE是等边三角形,
∴AD2=,
∴AD=1.
如图,过点D作DH⊥AB于H.
在△ADH中,∵∠HAD=45°,
∴DH=AD sin∠HAD=1×=.
故答案为.
12.解:∵两个相似三角形的周长比为4:9,
∴两个相似三角形的相似比为4:9,
∴两个相似三角形的面积比为16:81,
故答案为:16:81.
13.解:
∵BE分别平分ABC
∴∠ABE=∠EBC
∵在 ABCD中,DC∥AB
∴∠ABE=∠EBC=∠BEC
∴CE=BC=3
同理可得∠DAF=∠DFA,AD=DF=3
∵在 ABCD中,AB=DC=5
∴EF=1
∵在△EFG和△ABG中,
∴△EFG∽△ABG
∴==
故答案为:1:25
14.解:由题意得:∠DEF=∠DCA=90°,∠EDF=∠CDA,
∴△DEF∽△DCA,
则=,即=,
解得:AC=10,
故AB=AC+BC=10+1.5=11.5(米),
即旗杆的高度为11.5米;
故答案为:11.5.
15.解:如图所示,△A′BC即为所求.
16.解:∵∠ACB=90°,CD⊥AB,
∴CD2=AD BD=16,
则CD=4,
故答案为:4.
17.解:(1)∵四边形ABCD,AEFG是正方形,
∴∠BAC=∠GAF=45°,
∴∠BAF+∠FAC=∠FAC+∠GAC=45°,
∴∠HAG=∠BAF=18°,
∵∠DAG+∠GAH=∠DAC=45°,
∴∠DAG=45°﹣18°=27°,
故答案为:27.
(2)∵四边形ABCD,AEFG是正方形,
∴=,=,
∴=,
∵∠DAG+∠GAC=∠FAC+∠GAC=45°,
∴∠DAG=∠CAF,
∴△AFC∽△AGD;
(3)∵=,
设BF=k,CF=2k,则AB=BC=3k,
∴AF===k,AC=AB=3k,
∵四边形ABCD,AEFG是正方形,
∴∠AFH=∠ACF,∠FAH=∠CAF,
∴△AFH∽△ACF,
∴=,
∴==.
18.解:∵BC∥DE,
∴△ABC∽△ADE,
∴=,
∴=,
∴AB=17(m),
经检验:AB=17是分式方程的解,
答:河宽AB的长为17米.
19.解:(1)∵AB=AC,
∴∠B=∠C,
∵∠ADC=∠ADE+∠CDE=∠B+∠BAD,
而∠ADE=∠B,
∴∠BAD=∠CDE,
∴△ABD∽△DCE,
∴=,=,
∴y=﹣x2+x,
当x=4时,y=﹣×16+×4=,
即当D为BC的中点时,CE的长为;
(2)由(1)得y关于x的函数关系式为y=﹣x2+x(0≤x<8);
(3)∵∠AED>∠C,
而∠B=∠ADE=∠C,
∴∠AED>∠ADE,
∴AE<AD,
当DA=DE时,
∵△ABD∽△DCE,
∴=,即=1,
∴x=y,
∴﹣x2+x=x,解得x1=0,x2=2,
当EA=ED时,则∠EAD=∠ADE,
而∠ADE=∠C,
∴∠EAD=∠C,
∴△DAC∽△ABC,
∴=,即=,
∴x=,
综上所述,当△ADE为等腰三角形,x的值为0或2或.
20.解:(1)图1中共有3对相似三角形,分别为:△ABC∽△ACD,△ABC∽△CBD,△ACD∽△CBD.
故答案为3,△ABC∽△ACD,△ABC∽△CBD,△ACD∽△CBD;
(2)如图1,在△ABC中,∵∠ACB=90°,AB=10,AC=8,
∴BC==6.
∵△ABC的面积=AB CD=AC BC,
∴CD===4.8;
(3)存在点P,使以点B、P、Q为顶点的三角形与△ABC相似,理由如下:
在△BOC中,∵∠COB=90°,BC=6,OC=4.8,
∴OB==3.6.
分两种情况:
①当∠BQP=90°时,如图2①,此时△PQB∽△ACB,
∴=,
∴=,
解得t=2.25,即BQ=CP=2.25,
∴BP=BC﹣CP=6﹣2.25=3.75.
在△BPQ中,由勾股定理,得PQ===3,
∴点P的坐标为(1.35,3);
②当∠BPQ=90°时,如图2②,此时△QPB∽△ACB,
∴=,
∴=,
解得t=3.75,即BQ=CP=3.75,BP=BC﹣CP=6﹣3.75=2.25.
过点P作PE⊥x轴于点E.
∵△QPB∽△ACB,
∴=,即=,
∴PE=1.8.
在△BPE中,BE===1.35,
∴OE=OB﹣BE=3.6﹣1.35=2.25,
∴点P的坐标为(2.25,1.8).
综上可得,点P的坐标为(1.35,3)或(2.25,1.8).
21.解:设经x秒后,△PBQ∽△BCD,
由于∠PBQ=∠BCD=90°,
(1)当∠1=∠2时,有:,
即;
(2)当∠1=∠3时,有:,
即,
∴经过秒或2秒,△PBQ∽△BCD.
