北师大版高中数学必修2《平面与平面平行的判定》参考课件2(共15张PPT)
文档属性
| 名称 | 北师大版高中数学必修2《平面与平面平行的判定》参考课件2(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 10:38:59 | ||
图片预览




文档简介
(共15张PPT)
复习回顾:
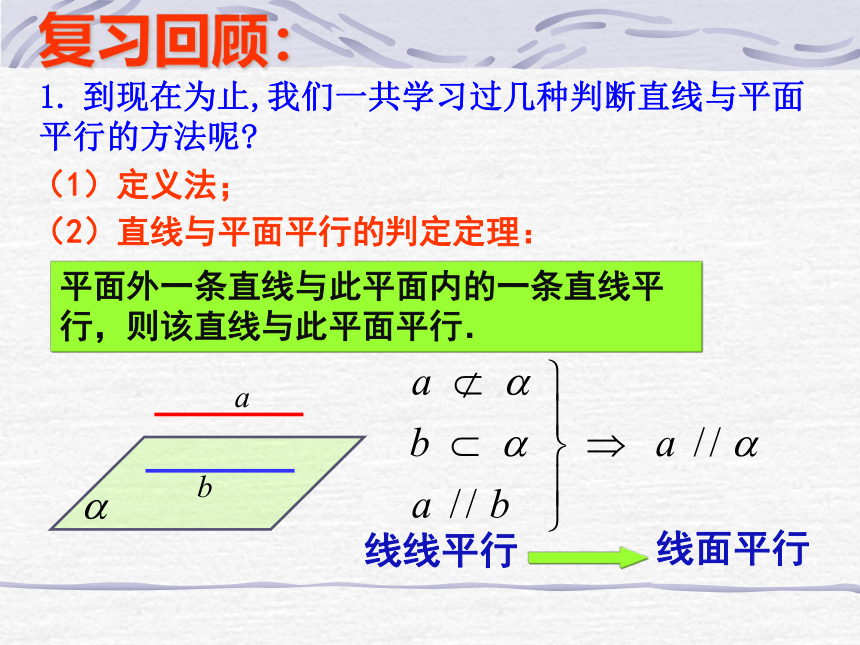
平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
(2)直线与平面平行的判定定理:
(1)定义法;
线线平行
线面平行
1. 到现在为止,我们一共学习过几种判断直线与平面平行的方法呢
(1)平行
(2)相交
α∥β
复习回顾:
怎样判定平面与平面平行呢?
2. 平面与平面有几种位置关系?分别是什么?
生活中有没有平面与平面平行的例子呢
(1)三角板或课本的一条边所在直线与桌面平行,这个三角板或课本所在平面与桌面平行吗?
(2)三角板或课本的两条边所在直线分别与桌面平行,情况又如何呢?
教室的天花板与地面给人平行的感觉,前后两块黑板也是平行的。
当三角板的两条边所在直线分别与地面平行时,这个三角板所在平面与地面平行。
(1)平面 内有一条直线与平面 平行, , 平行吗?
(2)平面 内有两条直线与平面 平行, , 平行吗?
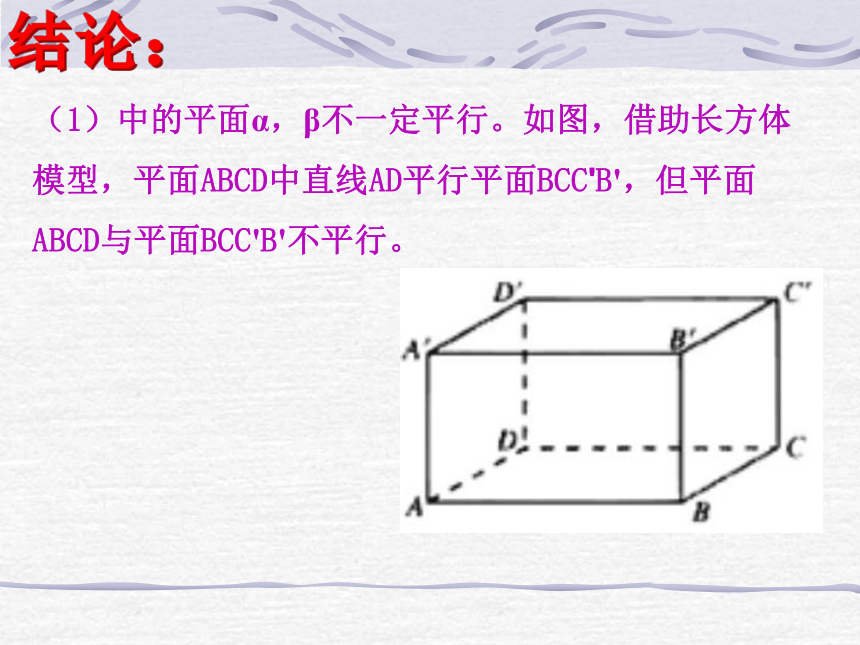
(1)中的平面α,β不一定平行。如图,借助长方体模型,平面ABCD中直线AD平行平面BCC'B',但平面ABCD与平面BCC'B'不平行。
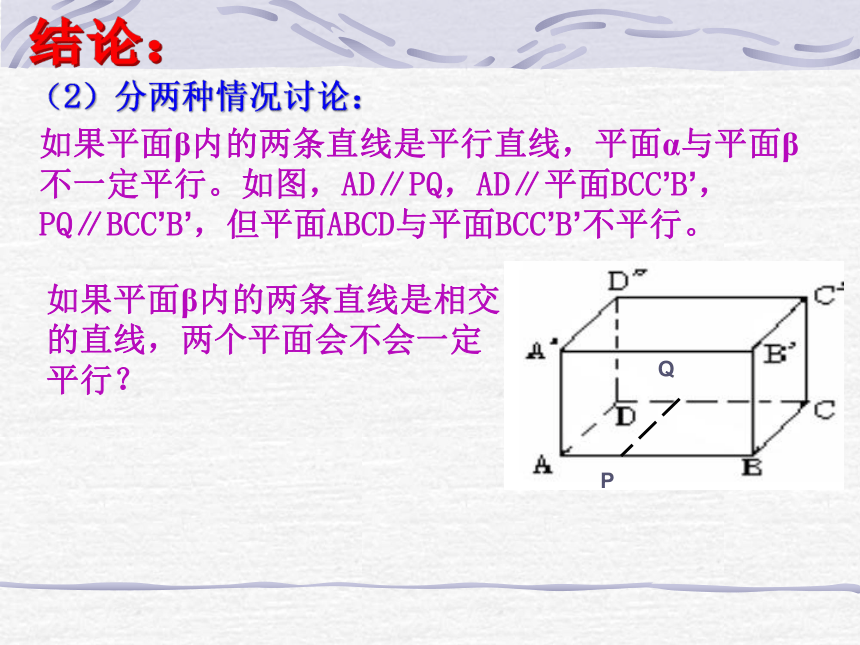
(2)分两种情况讨论:
如果平面β内的两条直线是平行直线,平面α与平面β不一定平行。如图,AD∥PQ,AD∥平面BCC’B’,PQ∥BCC’B’,但平面ABCD与平面BCC’B’不平行。
P
Q
如果平面β内的两条直线是相交的直线,两个平面会不会一定平行?
直线的条数不是关键
直线相交才是关键
如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行
两个平面平行的判定定理:
符号表示:
a ,b ,a b=P,a ,b
图形表示:
a
b
P
判断下列命题是否正确,并说明理由.
(1)若平面 内的两条直线分别与平面 平行,则
与 平行;
(2)若平面 内有无数条直线分别与平面 平行,则
与 平行;
(3)平行于同一直线的两个平面平行;
(4)两个平面分别经过两条平行直线,这两个平面平
行;
(5)过已知平面外一条直线,必能作出与已知平面平
行的平面.
×
×
×
×
×
例1:已知正方体ABCD-A1B1C1D1,求证:平面AB1D1//平面C1BD
证明:因为ABCD-A1B1C1D1为正方体,
所以 D1C1∥A1B1,D1C1=A1B1
又AB∥A1B1,AB=A1B1,
∴D1C1∥AB,D1C1=AB,
∴D1C1BA是平行四边形,
∴D1A∥C1B,
又D1A 平面C1BD,
C1B 平面C1BD.
由直线与平面平行的判定,可知
同理 D1B1∥平面C1BD,又 D1A∩D1B1=D1,
所以,平面AB1D1∥平面C1BD。
D1A∥平面C1BD,
变式:在正方体ABCD-A1B1C1D1中,
若 M、N、E、F分别是棱A1B1,A1D1,B1C1,C1D1的中点,求证:平面AMN//平面EFDB。
A
B
C
A1
B1
C1
D1
D
M
N
E
F
线面平行 面面平行
线线平行
1、如图:三棱锥P-ABC, D,E,F分别是棱PA,PB,PC中点,
求证:平面DEF∥平面ABC。
P
D
E
F
A
B
C
2、如图,B为△ACD所在平面外一点,M,N,G分别为△ABC,△ABD, △BCD的重心,求证:平面MNG∥平面ACD。
B
A
C
D
N·
M·
·G
第一步:在一个平面内找出两条相交直线;
第二步:证明两条相交直线分别平行于另一个平面。
第三步:利用判定定理得出结论。
小结:
1、面面平行的定义;
2、面面平行的判定定理;
3、面面平行判定定理的应用:要证面面平行,只要证线面平行,而要证线面平行,只要证线线平行。在立体几何中,往往通过线线、线面、面面间的位置关系的转化使问题得到解决。
复习回顾:
平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
(2)直线与平面平行的判定定理:
(1)定义法;
线线平行
线面平行
1. 到现在为止,我们一共学习过几种判断直线与平面平行的方法呢
(1)平行
(2)相交
α∥β
复习回顾:
怎样判定平面与平面平行呢?
2. 平面与平面有几种位置关系?分别是什么?
生活中有没有平面与平面平行的例子呢
(1)三角板或课本的一条边所在直线与桌面平行,这个三角板或课本所在平面与桌面平行吗?
(2)三角板或课本的两条边所在直线分别与桌面平行,情况又如何呢?
教室的天花板与地面给人平行的感觉,前后两块黑板也是平行的。
当三角板的两条边所在直线分别与地面平行时,这个三角板所在平面与地面平行。
(1)平面 内有一条直线与平面 平行, , 平行吗?
(2)平面 内有两条直线与平面 平行, , 平行吗?
(1)中的平面α,β不一定平行。如图,借助长方体模型,平面ABCD中直线AD平行平面BCC'B',但平面ABCD与平面BCC'B'不平行。
(2)分两种情况讨论:
如果平面β内的两条直线是平行直线,平面α与平面β不一定平行。如图,AD∥PQ,AD∥平面BCC’B’,PQ∥BCC’B’,但平面ABCD与平面BCC’B’不平行。
P
Q
如果平面β内的两条直线是相交的直线,两个平面会不会一定平行?
直线的条数不是关键
直线相交才是关键
如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行
两个平面平行的判定定理:
符号表示:
a ,b ,a b=P,a ,b
图形表示:
a
b
P
判断下列命题是否正确,并说明理由.
(1)若平面 内的两条直线分别与平面 平行,则
与 平行;
(2)若平面 内有无数条直线分别与平面 平行,则
与 平行;
(3)平行于同一直线的两个平面平行;
(4)两个平面分别经过两条平行直线,这两个平面平
行;
(5)过已知平面外一条直线,必能作出与已知平面平
行的平面.
×
×
×
×
×
例1:已知正方体ABCD-A1B1C1D1,求证:平面AB1D1//平面C1BD
证明:因为ABCD-A1B1C1D1为正方体,
所以 D1C1∥A1B1,D1C1=A1B1
又AB∥A1B1,AB=A1B1,
∴D1C1∥AB,D1C1=AB,
∴D1C1BA是平行四边形,
∴D1A∥C1B,
又D1A 平面C1BD,
C1B 平面C1BD.
由直线与平面平行的判定,可知
同理 D1B1∥平面C1BD,又 D1A∩D1B1=D1,
所以,平面AB1D1∥平面C1BD。
D1A∥平面C1BD,
变式:在正方体ABCD-A1B1C1D1中,
若 M、N、E、F分别是棱A1B1,A1D1,B1C1,C1D1的中点,求证:平面AMN//平面EFDB。
A
B
C
A1
B1
C1
D1
D
M
N
E
F
线面平行 面面平行
线线平行
1、如图:三棱锥P-ABC, D,E,F分别是棱PA,PB,PC中点,
求证:平面DEF∥平面ABC。
P
D
E
F
A
B
C
2、如图,B为△ACD所在平面外一点,M,N,G分别为△ABC,△ABD, △BCD的重心,求证:平面MNG∥平面ACD。
B
A
C
D
N·
M·
·G
第一步:在一个平面内找出两条相交直线;
第二步:证明两条相交直线分别平行于另一个平面。
第三步:利用判定定理得出结论。
小结:
1、面面平行的定义;
2、面面平行的判定定理;
3、面面平行判定定理的应用:要证面面平行,只要证线面平行,而要证线面平行,只要证线线平行。在立体几何中,往往通过线线、线面、面面间的位置关系的转化使问题得到解决。
