北师大版高中数学必修2《圆的一般方程》参考课件(共24张PPT)
文档属性
| 名称 | 北师大版高中数学必修2《圆的一般方程》参考课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 882.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
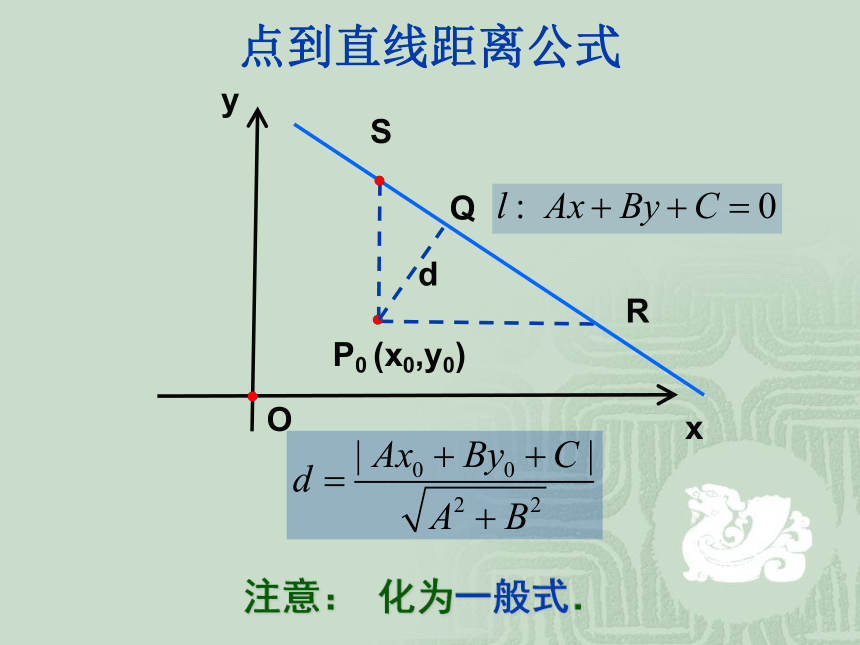
点到直线距离公式
x
y
P0 (x0,y0)
O
S
R
Q
d
注意: 化为一般式.
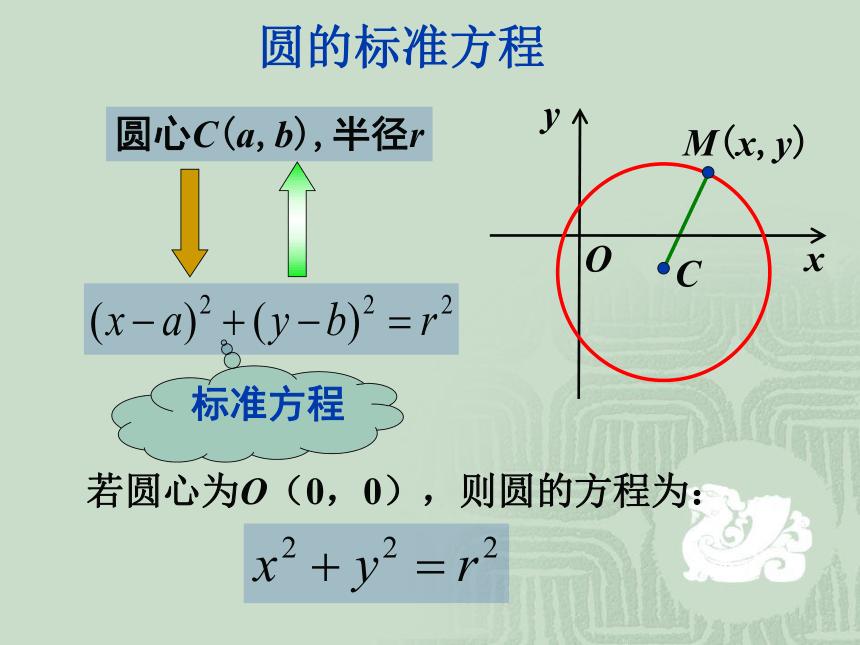
圆的标准方程
x
y
O
C
M(x,y)
圆心C(a,b),半径r
若圆心为O(0,0),则圆的方程为:
标准方程
圆心 (2, -4) ,半径
求圆心和半径
⑴圆 (x-1)2+ (y-1)2=9
⑵圆 (x-2)2+ (y+4)2=2
⑶圆 (x+1)2+ (y+2)2=m2
圆心 (1, 1) ,半径3
圆心 (-1, -2) ,半径|m|
圆的一般方程
展开得
任何一个圆的方程都是二元二次方程
反之是否成立?
圆的一般方程
配方得
不一定是圆
以(1,-2)为圆心,以2为半径的圆
配方得
不是圆
练习
判断下列方程是不是表示圆
以(2,3)为圆心,以3为半径的圆
表示点(2,3)
不表示任何图形
展开圆的标准方程
(x-a)2+(y-b)2=r2
得:x2+y2-2ax-2by+a2+b2-r2=0
即:x2+y2+Dx+Ey+F=0(1)
可见任何圆的方程都可以写成(1)式,
不妨设:D=-2a、E=-2b、F=a2+b2-r2
圆的一般方程
(1)当 时,
表示圆,
(2)当 时,
表示点
(3)当 时,
不表示任何图形
(x-a)2+(y-b)2 =r2
两种方程的字母间的关系:
形式特点:(1)x2和y2的系数相同,不等于0
(2)没有xy这样的项。
练习1:下列方程各表示什么图形
原点(0,0)
练习2 :将下列各圆方程化为标准方程,
并求圆的半径和圆心坐标.
(1)圆心(-3,0),半径3.
(2)圆心(0,b),半径|b|.
若已知条件涉及圆心和半径,
我们一般采用圆的标准方程较简单.
练习:
若已知三点求圆的方程,我们常采用圆的
一般方程用待定系数法求解.
练习:
把点A,B,C的坐标代入得方程组
所求圆的方程为:
小结
(1)当 时,
表示圆,
(2)当 时,
表示点
(3)当 时,
不表示任何图形
例2. 已知一曲线是与定点O(0,0),A(3,0)距离的比是
求此曲线的轨迹方程,并画出曲线
的点的轨迹,
解:在给定的坐标系里,设点M(x,y)是曲线上的任意一点,也就是点M属于集合
由两点间的距离公式,得
化简得
x2+y2+2x 3=0 ①
这就是所求的曲线方程.
把方程①的左边配方,得(x+1)2+y2=4.
所以方程②的曲线是以C( 1,0)为圆心,2为半径的圆
x
y
M
A
O
C
.
O
.
.
y
x
(-1,0)
A(3,0)
M
例2:已知一曲线是与两个定点O(0,0),A(3,0)距离的比为 的点的轨迹,求此曲线的方程,并画出曲线。
1
2
[简单的思考与应用]
(1)已知圆 的圆心坐标为
(-2,3),半径为4,则D,E,F分别等于
是圆的方程的充要条件是
(3)圆 与 轴相切,则这个圆截
轴所得的弦长是
(4)点 是圆 的一条弦的中点,
则这条弦所在的直线方程是
例题. 自点A(-3,3)发射的光线l 射到x轴上,被x轴反射,
其反射光线所在的直线与圆x2+y2-4x-4y+7=0相切,
求光线l 所在直线的方程.
B(-3,-3)
A(-3,3)
C(2, 2)
入射光线及反射光线与
x轴夹角相等.
(2)点P关于x轴的对称点Q在
反射光线所在的直线l 上.
(3)圆心C到l 的距离等于
圆的半径.
答案: l : 4x+3y+3=0或3x+4y-3=0
例:求过三点A(5,1),B (7,-3),C(2,8)的圆的方程
圆心:两条弦的中垂线的交点
半径:圆心到圆上一点
x
y
O
E
A(5,1)
B(7,-3)
C(2,-8)
几何方法
方法一:
方法二:待定系数法
待定系数法
解:设所求圆的方程为:
因为A(5,1),B (7,-3),C(2,8)都在圆上
所求圆的方程为
方法三:待定系数法
解:设所求圆的方程为:
因为A(5,1),B (7,-3),C(2,8)都在圆上
所求圆的方程为
小结:求圆的方程
几何方法
求圆心坐标 (两条直线的交点)(常用弦的中垂线)
求 半径 (圆心到圆上一点的距离)
写出圆的标准方程
待定系数法
列关于a,b,r(或D,E,F)的方程组
解出a,b,r(或D,E,F),写出标准方程(或一般方程)
点到直线距离公式
x
y
P0 (x0,y0)
O
S
R
Q
d
注意: 化为一般式.
圆的标准方程
x
y
O
C
M(x,y)
圆心C(a,b),半径r
若圆心为O(0,0),则圆的方程为:
标准方程
圆心 (2, -4) ,半径
求圆心和半径
⑴圆 (x-1)2+ (y-1)2=9
⑵圆 (x-2)2+ (y+4)2=2
⑶圆 (x+1)2+ (y+2)2=m2
圆心 (1, 1) ,半径3
圆心 (-1, -2) ,半径|m|
圆的一般方程
展开得
任何一个圆的方程都是二元二次方程
反之是否成立?
圆的一般方程
配方得
不一定是圆
以(1,-2)为圆心,以2为半径的圆
配方得
不是圆
练习
判断下列方程是不是表示圆
以(2,3)为圆心,以3为半径的圆
表示点(2,3)
不表示任何图形
展开圆的标准方程
(x-a)2+(y-b)2=r2
得:x2+y2-2ax-2by+a2+b2-r2=0
即:x2+y2+Dx+Ey+F=0(1)
可见任何圆的方程都可以写成(1)式,
不妨设:D=-2a、E=-2b、F=a2+b2-r2
圆的一般方程
(1)当 时,
表示圆,
(2)当 时,
表示点
(3)当 时,
不表示任何图形
(x-a)2+(y-b)2 =r2
两种方程的字母间的关系:
形式特点:(1)x2和y2的系数相同,不等于0
(2)没有xy这样的项。
练习1:下列方程各表示什么图形
原点(0,0)
练习2 :将下列各圆方程化为标准方程,
并求圆的半径和圆心坐标.
(1)圆心(-3,0),半径3.
(2)圆心(0,b),半径|b|.
若已知条件涉及圆心和半径,
我们一般采用圆的标准方程较简单.
练习:
若已知三点求圆的方程,我们常采用圆的
一般方程用待定系数法求解.
练习:
把点A,B,C的坐标代入得方程组
所求圆的方程为:
小结
(1)当 时,
表示圆,
(2)当 时,
表示点
(3)当 时,
不表示任何图形
例2. 已知一曲线是与定点O(0,0),A(3,0)距离的比是
求此曲线的轨迹方程,并画出曲线
的点的轨迹,
解:在给定的坐标系里,设点M(x,y)是曲线上的任意一点,也就是点M属于集合
由两点间的距离公式,得
化简得
x2+y2+2x 3=0 ①
这就是所求的曲线方程.
把方程①的左边配方,得(x+1)2+y2=4.
所以方程②的曲线是以C( 1,0)为圆心,2为半径的圆
x
y
M
A
O
C
.
O
.
.
y
x
(-1,0)
A(3,0)
M
例2:已知一曲线是与两个定点O(0,0),A(3,0)距离的比为 的点的轨迹,求此曲线的方程,并画出曲线。
1
2
[简单的思考与应用]
(1)已知圆 的圆心坐标为
(-2,3),半径为4,则D,E,F分别等于
是圆的方程的充要条件是
(3)圆 与 轴相切,则这个圆截
轴所得的弦长是
(4)点 是圆 的一条弦的中点,
则这条弦所在的直线方程是
例题. 自点A(-3,3)发射的光线l 射到x轴上,被x轴反射,
其反射光线所在的直线与圆x2+y2-4x-4y+7=0相切,
求光线l 所在直线的方程.
B(-3,-3)
A(-3,3)
C(2, 2)
入射光线及反射光线与
x轴夹角相等.
(2)点P关于x轴的对称点Q在
反射光线所在的直线l 上.
(3)圆心C到l 的距离等于
圆的半径.
答案: l : 4x+3y+3=0或3x+4y-3=0
例:求过三点A(5,1),B (7,-3),C(2,8)的圆的方程
圆心:两条弦的中垂线的交点
半径:圆心到圆上一点
x
y
O
E
A(5,1)
B(7,-3)
C(2,-8)
几何方法
方法一:
方法二:待定系数法
待定系数法
解:设所求圆的方程为:
因为A(5,1),B (7,-3),C(2,8)都在圆上
所求圆的方程为
方法三:待定系数法
解:设所求圆的方程为:
因为A(5,1),B (7,-3),C(2,8)都在圆上
所求圆的方程为
小结:求圆的方程
几何方法
求圆心坐标 (两条直线的交点)(常用弦的中垂线)
求 半径 (圆心到圆上一点的距离)
写出圆的标准方程
待定系数法
列关于a,b,r(或D,E,F)的方程组
解出a,b,r(或D,E,F),写出标准方程(或一般方程)
