北师大版高中数学必修2《直线的倾斜角和斜率》参考课件2(共25张PPT)
文档属性
| 名称 | 北师大版高中数学必修2《直线的倾斜角和斜率》参考课件2(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
神六为何如此完美?
太空飞行中的神六
如果代数与几何各自分开发展,那它的进步将十分缓慢,而且应用范围也很有限.但若两者互相结合而共同发展,则就会相互加强,并以快速的步伐向着完美化的方向猛进.
—拉格朗日
平面解析几何研究的主要问题是:
(1) 根据已知条件,求出表示平面曲线的方程;
(2)通过方程研究平面曲线的性质。
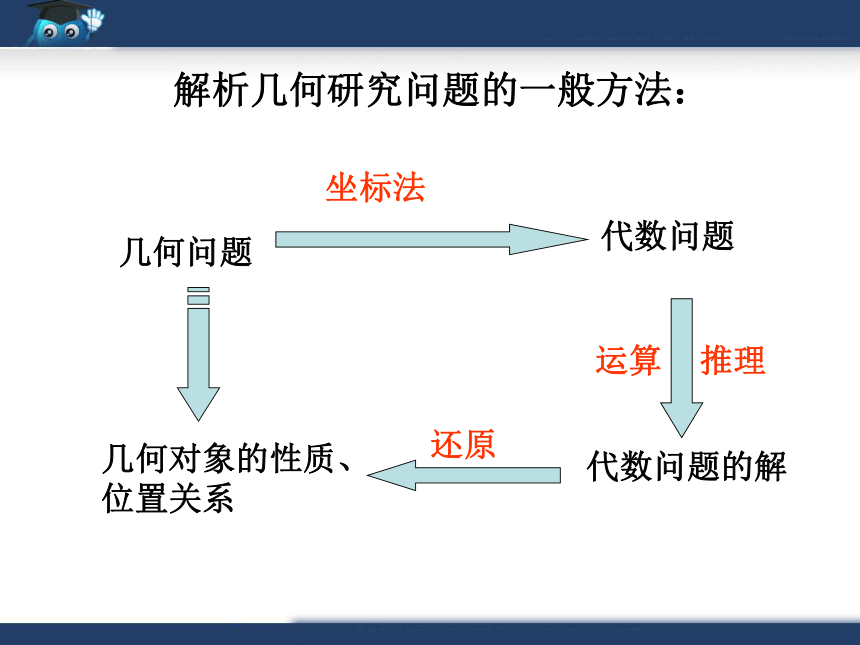
解析几何研究问题的一般方法:
几何对象的性质、位置关系
几何问题
代数问题
代数问题的解
坐标法
还原
运算 推理
如果你手中只有一把斜边长度小于下图中对角线长度的等腰直角三角形直尺,你能画出下图中的对角线吗?
一个点和直线的方向.
确定直线位置的几何要素有两个:
结论:坡度越大,楼梯越陡.
0.8m
1m
0.4m
类似地,如果我们也想给直线用一个新的量来表示倾斜程度,我们把这一个量叫斜率,那么应该怎样定义斜率呢?
O
x
y
O
P(1,k)
Q(1,0)
R(2, )
S(2,0)
x
y
O
P(1,k)
Q(1,0)
R(2, 2k)
S(2,0)
2k-k
2-1
直线的斜率的定义:
O
如果 ,那么直线PQ的斜率不存在.
如果
,
l2
l1
l3
例1
如图,直线l1, l2 , l3 都经过P(3, 2),
又 l1, l2 , l3 分别经过点Q1 (-2 ,-1) ,
Q2 (4, -2 ) , Q3 (-3, 2 ) ,试计算直线
l1, l2 ,l3的斜率.
O
x
y
4
-4
-4
4
P
Q1
Q3
Q2
k2=-4
k3=0
x
.
p
y
O
(3)
k不存在
x
.
p
y
O
(2)
k<0
x
.
p
y
O
(1)
k>0
x
.
p
y
O
(4)
k=0
思考1:
1.三点A(0,2), B( 2,5), C(4,8),
其中kAB ,kAC , kBC 怎样?
2.三点(1,-1), (3,3), (5,a)在一
条直线上,求a的值.
思考2:
例2 经过点(3,2)画直线,使直线的斜率分别为:
思考3:
如果直线l按x轴负方向平移3个单位,再沿y轴正方向平移1个单位后,又回到了原来的位置,那么直线l的斜率为多少?
例3 直线l过点M(-1,1),且与以P(2,2),Q(3,3)为两端点的线段PQ有公共点,求直线l的斜率的取值范围.
思考4:
求函数
(2≤x≤3)的值域.
小结提高
楼梯坡度
核心
知识 方法 思想
几何意义
直线的斜率
斜率定义
平面解析几何
应用
(2)已知三点A(3, -1), B (-2,-1), C (0, 2),求直线AB、AC、BC的斜率.
O
x
y
4
-4
-4
4
A
B
C
神六为何如此完美?
太空飞行中的神六
如果代数与几何各自分开发展,那它的进步将十分缓慢,而且应用范围也很有限.但若两者互相结合而共同发展,则就会相互加强,并以快速的步伐向着完美化的方向猛进.
—拉格朗日
平面解析几何研究的主要问题是:
(1) 根据已知条件,求出表示平面曲线的方程;
(2)通过方程研究平面曲线的性质。
解析几何研究问题的一般方法:
几何对象的性质、位置关系
几何问题
代数问题
代数问题的解
坐标法
还原
运算 推理
如果你手中只有一把斜边长度小于下图中对角线长度的等腰直角三角形直尺,你能画出下图中的对角线吗?
一个点和直线的方向.
确定直线位置的几何要素有两个:
结论:坡度越大,楼梯越陡.
0.8m
1m
0.4m
类似地,如果我们也想给直线用一个新的量来表示倾斜程度,我们把这一个量叫斜率,那么应该怎样定义斜率呢?
O
x
y
O
P(1,k)
Q(1,0)
R(2, )
S(2,0)
x
y
O
P(1,k)
Q(1,0)
R(2, 2k)
S(2,0)
2k-k
2-1
直线的斜率的定义:
O
如果 ,那么直线PQ的斜率不存在.
如果
,
l2
l1
l3
例1
如图,直线l1, l2 , l3 都经过P(3, 2),
又 l1, l2 , l3 分别经过点Q1 (-2 ,-1) ,
Q2 (4, -2 ) , Q3 (-3, 2 ) ,试计算直线
l1, l2 ,l3的斜率.
O
x
y
4
-4
-4
4
P
Q1
Q3
Q2
k2=-4
k3=0
x
.
p
y
O
(3)
k不存在
x
.
p
y
O
(2)
k<0
x
.
p
y
O
(1)
k>0
x
.
p
y
O
(4)
k=0
思考1:
1.三点A(0,2), B( 2,5), C(4,8),
其中kAB ,kAC , kBC 怎样?
2.三点(1,-1), (3,3), (5,a)在一
条直线上,求a的值.
思考2:
例2 经过点(3,2)画直线,使直线的斜率分别为:
思考3:
如果直线l按x轴负方向平移3个单位,再沿y轴正方向平移1个单位后,又回到了原来的位置,那么直线l的斜率为多少?
例3 直线l过点M(-1,1),且与以P(2,2),Q(3,3)为两端点的线段PQ有公共点,求直线l的斜率的取值范围.
思考4:
求函数
(2≤x≤3)的值域.
小结提高
楼梯坡度
核心
知识 方法 思想
几何意义
直线的斜率
斜率定义
平面解析几何
应用
(2)已知三点A(3, -1), B (-2,-1), C (0, 2),求直线AB、AC、BC的斜率.
O
x
y
4
-4
-4
4
A
B
C
