6.1 圆周运动练习(Word版,含解析)
文档属性
| 名称 | 6.1 圆周运动练习(Word版,含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 217.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-11-24 06:22:57 | ||
图片预览




文档简介
圆周运动
基础练
1.一个物体以恒定角速度ω做匀速圆周运动时,下列说法正确的是( )
A.轨道半径越大线速度越小
B.轨道半径越大线速度越大
C.轨道半径越大周期越大
D.轨道半径越大周期越小
2.如图所示,一个小球绕圆心O做匀速圆周运动,已知圆周半径为r,该小球运动的角速度为ω,则它运动的线速度大小为( )
A. B.ωr
C.ω2r D.ωr2
3.在一棵大树将要被伐倒的时候,有经验的伐木工人会双眼紧盯着树梢,根据树梢的运动情况来判断大树正在朝哪个方向倒下,从而避免被倒下的大树砸伤,从物理知识的角度来解释,下列说法正确的是( )
A.树木倒下时,树梢的角速度较大,易于判断
B.树木倒下时,树梢的线速度较大,易于判断
C.树木倒下时,树梢的周期较大,易于判断
D.伐木工人的经验没有科学依据
4.下图为一种早期的自行车,这种自行车前轮的直径很大,这样的设计在当时主要是为了( )
A.提高速度 B.提高稳定性
C.骑行方便 D.减小阻力
5.如图所示,当用扳手拧螺母时,扳手上的P、Q两点的角速度分别为ωP和ωQ,线速度大小分别为vP和vQ,则( )
A.ωP=ωQ,vPC.ωP<ωQ,vP=vQ D.ωP=ωQ,vP>vQ
6.做匀速圆周运动的物体,20 s内沿半径为10 m的圆周运动了100 m,试求物体做匀速圆周运动时:
(1)线速度的大小;
(2)角速度的大小;
(3)周期的大小。
7.一个圆环以竖直直径AB为轴匀速转动,如图所示。
(1)求环上M、N两点的线速度的大小之比;
(2)求M、N的角速度之比。
提升练
1.某品牌的机械鼠标内部结构如图所示,机械鼠标中的定位球的直径是2.0 cm,某次操作中,鼠标沿直线匀速移动了12 cm,耗时1 s,则定位球的角速度为( )
A. rad/s B. rad/s
C.6 rad/s D.12 rad/s
2.某品牌手动榨汁机如图所示,榨汁时手柄绕O点旋转,则手柄上B、C两点的周期、角速度及线速度等物理量的关系是( )
A.TB=TC,vB>vC B.TB=TC,vBC.ωB>ωC,vB=vC D.ωB<ωC,vB3.(多选)明代出版的《天工开物》一书中有牛力齿轮水车图(如图所示),记录了我们祖先的劳动智慧。若A、B两齿轮车半径的大小关系为RA>RB,则( )
A.齿轮A的角速度比齿轮B的小
B.齿轮A与齿轮B的角速度大小相等
C.齿轮A边缘的线速度比齿轮B边缘的大
D.齿轮A与齿轮B边缘的线速度大小相等
4.(多选)无级变速可在变速范围内任意连续地变换速度,性能优于传统的挡位变速,很多种高档汽车都应用了无级变速。下图是截锥式无级变速模型示意图,两个锥轮之间有一个滚轮,主动轮、滚轮、从动轮之间靠着彼此之间的摩擦力带动。以下判断正确的是( )
A.主动轮转速不变,当位于主动轮与从动轮之间的滚轮从右向左移动时,从动轮转速减小,滚轮从左向右移动时,从动轮转速增大
B.主动轮转速不变,当位于主动轮与从动轮之间的滚轮从左向右移动时,从动轮转速减小,滚轮从右向左移动时,从动轮转速增大
C.当滚轮位于主动轮直径为D1、从动轮直径为D2的位置上时,主动轮转速n1、从动轮转速n2之间的关系为n2=n1
D.当滚轮位于主动轮直径为D1、从动轮直径为D2的位置上时,主动轮转速n1、从动轮转速n2之间的关系为n2=n1
5.下图是教室里的石英钟,设时针、分针长度之比为5∶6,求:
(1)时针、分针的角速度之比与针尖的线速度之比;
(2)从图中位置(2:00)开始计时,时针、分针经过多长时间将第一次重合
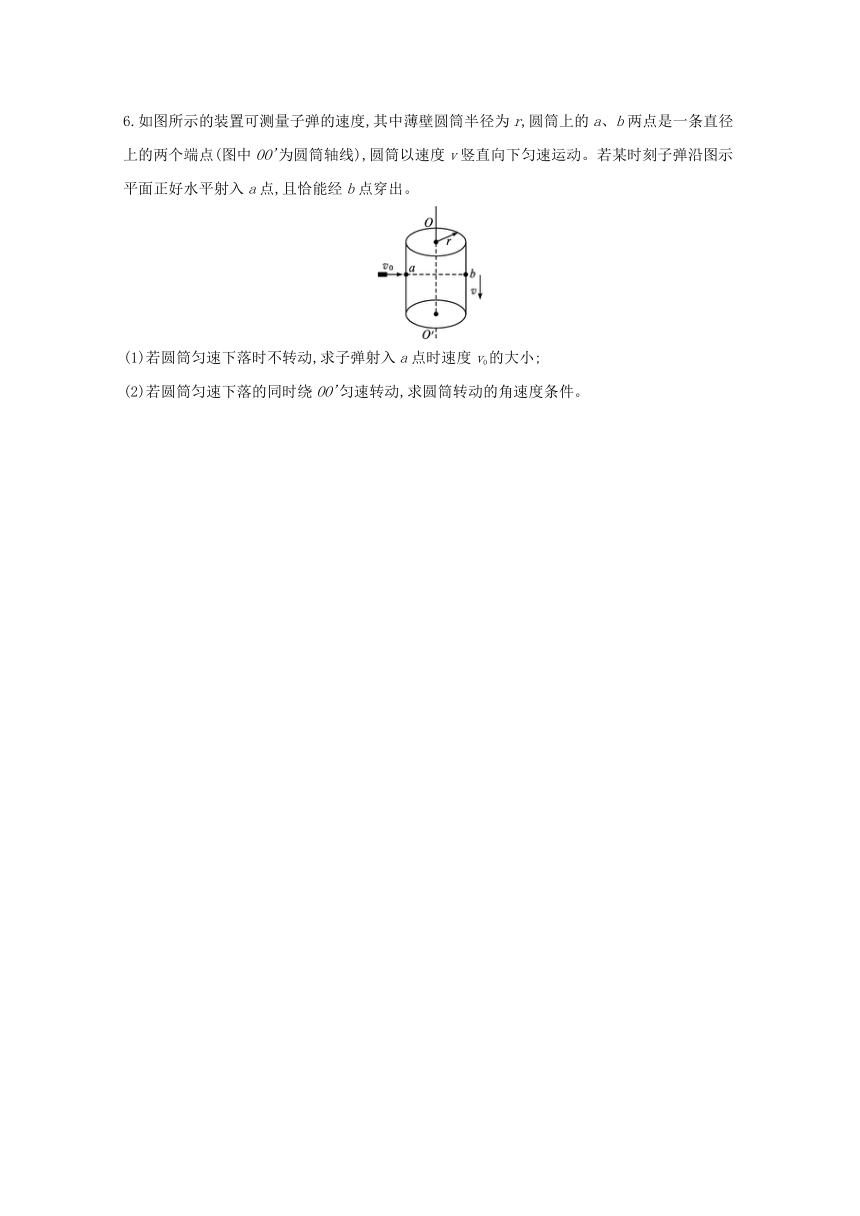
6.如图所示的装置可测量子弹的速度,其中薄壁圆筒半径为r,圆筒上的a、b两点是一条直径上的两个端点(图中OO'为圆筒轴线),圆筒以速度v竖直向下匀速运动。若某时刻子弹沿图示平面正好水平射入a点,且恰能经b点穿出。
(1)若圆筒匀速下落时不转动,求子弹射入a点时速度v0的大小;
(2)若圆筒匀速下落的同时绕OO'匀速转动,求圆筒转动的角速度条件。
参考答案:
基础练
1.一个物体以恒定角速度ω做匀速圆周运动时,下列说法正确的是( )
A.轨道半径越大线速度越小
B.轨道半径越大线速度越大
C.轨道半径越大周期越大
D.轨道半径越大周期越小
解析:物体以一定的角速度做匀速圆周运动,由v=ωr得,v与r成正比,所以当半径越大时,线速度也越大,故B正确,A错误;由ω=得,T与ω成反比,与半径无关,因此周期不变,故C、D错误。
答案:B
2.如图所示,一个小球绕圆心O做匀速圆周运动,已知圆周半径为r,该小球运动的角速度为ω,则它运动的线速度大小为( )
A. B.ωr
C.ω2r D.ωr2
解析:小球做匀速圆周运动,转动的半径为r,角速度为ω,故线速度为v=ωr,B正确。
答案:B
3.在一棵大树将要被伐倒的时候,有经验的伐木工人会双眼紧盯着树梢,根据树梢的运动情况来判断大树正在朝哪个方向倒下,从而避免被倒下的大树砸伤,从物理知识的角度来解释,下列说法正确的是( )
A.树木倒下时,树梢的角速度较大,易于判断
B.树木倒下时,树梢的线速度较大,易于判断
C.树木倒下时,树梢的周期较大,易于判断
D.伐木工人的经验没有科学依据
解析:整个大树的角速度和周期相同,树梢的转动半径大,线速度大。
答案:B
4.下图为一种早期的自行车,这种自行车前轮的直径很大,这样的设计在当时主要是为了( )
A.提高速度 B.提高稳定性
C.骑行方便 D.减小阻力
解析:在骑车人脚蹬踏板转速一定的情况下,据公式v=2πrn知,轮子半径越大,车轮边缘的线速度越大,车行驶得也就越快,故A选项正确。
答案:A
5.如图所示,当用扳手拧螺母时,扳手上的P、Q两点的角速度分别为ωP和ωQ,线速度大小分别为vP和vQ,则( )
A.ωP=ωQ,vPC.ωP<ωQ,vP=vQ D.ωP=ωQ,vP>vQ
解析:由于P、Q两点属于同轴转动,所以P、Q两点的角速度是相等的,即ωP=ωQ;同时由图可知Q点到螺母的距离比较大,所以Q点的线速度大,即vP答案:A
6.做匀速圆周运动的物体,20 s内沿半径为10 m的圆周运动了100 m,试求物体做匀速圆周运动时:
(1)线速度的大小;
(2)角速度的大小;
(3)周期的大小。
解析:(1)依据线速度的定义式可得
v=m/s=5m/s。
(2)依据v=ωr可得
ω=rad/s=0.5rad/s。
(3)T=s=4πs。
答案:(1)5 m/s (2)0.5 rad/s (3)4π s
7.一个圆环以竖直直径AB为轴匀速转动,如图所示。
(1)求环上M、N两点的线速度的大小之比;
(2)求M、N的角速度之比。
解析:M、N是同一环上的两点,它们与环具有相同的角速度,即ωM∶ωN=1∶1,两点做圆周运动的半径之比rM∶rN=sin60°∶sin30°=∶1,故vM∶vN=ωMrM∶ωNrN=∶1。
答案:(1)∶1 (2)1∶1
提升练
1.某品牌的机械鼠标内部结构如图所示,机械鼠标中的定位球的直径是2.0 cm,某次操作中,鼠标沿直线匀速移动了12 cm,耗时1 s,则定位球的角速度为( )
A. rad/s B. rad/s
C.6 rad/s D.12 rad/s
解析:根据线速度定义式得,定位球的线速度为v=cm/s=12cm/s;由角速度与线速度关系v=ωr,得定位球的角速度为ω=rad/s=12rad/s,D正确。
答案:D
2.某品牌手动榨汁机如图所示,榨汁时手柄绕O点旋转,则手柄上B、C两点的周期、角速度及线速度等物理量的关系是( )
A.TB=TC,vB>vC B.TB=TC,vBC.ωB>ωC,vB=vC D.ωB<ωC,vB解析:手柄上B、C两点属于共轴转动,具有相同的角速度,即ωB=ωC,由T=知周期相等,即TB=TC,由圆周运动的线速度与角速度关系v=ωr,结合rB答案:B
3.(多选)明代出版的《天工开物》一书中有牛力齿轮水车图(如图所示),记录了我们祖先的劳动智慧。若A、B两齿轮车半径的大小关系为RA>RB,则( )
A.齿轮A的角速度比齿轮B的小
B.齿轮A与齿轮B的角速度大小相等
C.齿轮A边缘的线速度比齿轮B边缘的大
D.齿轮A与齿轮B边缘的线速度大小相等
解析:齿轮A与齿轮B是同缘传动,边缘点的线速度相等,即vA=vB,根据公式v=ωr可知,半径比较大的齿轮A的角速度小于半径比较小的齿轮B的角速度,即ωA<ωB,故A、D正确,B、C错误。
答案:AD
4.(多选)无级变速可在变速范围内任意连续地变换速度,性能优于传统的挡位变速,很多种高档汽车都应用了无级变速。下图是截锥式无级变速模型示意图,两个锥轮之间有一个滚轮,主动轮、滚轮、从动轮之间靠着彼此之间的摩擦力带动。以下判断正确的是( )
A.主动轮转速不变,当位于主动轮与从动轮之间的滚轮从右向左移动时,从动轮转速减小,滚轮从左向右移动时,从动轮转速增大
B.主动轮转速不变,当位于主动轮与从动轮之间的滚轮从左向右移动时,从动轮转速减小,滚轮从右向左移动时,从动轮转速增大
C.当滚轮位于主动轮直径为D1、从动轮直径为D2的位置上时,主动轮转速n1、从动轮转速n2之间的关系为n2=n1
D.当滚轮位于主动轮直径为D1、从动轮直径为D2的位置上时,主动轮转速n1、从动轮转速n2之间的关系为n2=n1
解析:设某一时刻,滚轮位于主动轮直径为D1、从动轮直径为D2的位置上,三个轮的轮缘的线速度相等,得n1D1=n2D2,即n2=n1,故C选项正确,D选项错误;当位于主动轮与从动轮之间的滚轮从左向右移动时,D1变小,D2变大,在n1不变的情况下,n2变小,反之,当滚轮从右向左移动时,D1变大,D2变小,在n1不变的情况下,n2变大,故B选项正确,A选项错误。
答案:BC
5.下图是教室里的石英钟,设时针、分针长度之比为5∶6,求:
(1)时针、分针的角速度之比与针尖的线速度之比;
(2)从图中位置(2:00)开始计时,时针、分针经过多长时间将第一次重合
解析:(1)时针的周期T1=12h,分针的周期T2=1h
因此ω1∶ω2==1∶12
v1∶v2=ω1r1∶ω2r2=5∶72。
(2)设经过时间t时针、分针第一次重合,则ω2t-ω1t=t=
解得t=h。
答案:(1)1∶12 5∶72 (2) h
6.如图所示的装置可测量子弹的速度,其中薄壁圆筒半径为r,圆筒上的a、b两点是一条直径上的两个端点(图中OO'为圆筒轴线),圆筒以速度v竖直向下匀速运动。若某时刻子弹沿图示平面正好水平射入a点,且恰能经b点穿出。
(1)若圆筒匀速下落时不转动,求子弹射入a点时速度v0的大小;
(2)若圆筒匀速下落的同时绕OO'匀速转动,求圆筒转动的角速度条件。
解析:(1)子弹做平抛运动,水平方向2r=v0t
竖直方向vt=gt2
解得v0=。
(2)圆筒转动的角度是2π的整数倍
2πn=ωt(n=1,2,3,…)
下落时间t=
解得ω=(n=1,2,3,…)。
答案:(1)
(2)ω=(n=1,2,3,…)
基础练
1.一个物体以恒定角速度ω做匀速圆周运动时,下列说法正确的是( )
A.轨道半径越大线速度越小
B.轨道半径越大线速度越大
C.轨道半径越大周期越大
D.轨道半径越大周期越小
2.如图所示,一个小球绕圆心O做匀速圆周运动,已知圆周半径为r,该小球运动的角速度为ω,则它运动的线速度大小为( )
A. B.ωr
C.ω2r D.ωr2
3.在一棵大树将要被伐倒的时候,有经验的伐木工人会双眼紧盯着树梢,根据树梢的运动情况来判断大树正在朝哪个方向倒下,从而避免被倒下的大树砸伤,从物理知识的角度来解释,下列说法正确的是( )
A.树木倒下时,树梢的角速度较大,易于判断
B.树木倒下时,树梢的线速度较大,易于判断
C.树木倒下时,树梢的周期较大,易于判断
D.伐木工人的经验没有科学依据
4.下图为一种早期的自行车,这种自行车前轮的直径很大,这样的设计在当时主要是为了( )
A.提高速度 B.提高稳定性
C.骑行方便 D.减小阻力
5.如图所示,当用扳手拧螺母时,扳手上的P、Q两点的角速度分别为ωP和ωQ,线速度大小分别为vP和vQ,则( )
A.ωP=ωQ,vP
6.做匀速圆周运动的物体,20 s内沿半径为10 m的圆周运动了100 m,试求物体做匀速圆周运动时:
(1)线速度的大小;
(2)角速度的大小;
(3)周期的大小。
7.一个圆环以竖直直径AB为轴匀速转动,如图所示。
(1)求环上M、N两点的线速度的大小之比;
(2)求M、N的角速度之比。
提升练
1.某品牌的机械鼠标内部结构如图所示,机械鼠标中的定位球的直径是2.0 cm,某次操作中,鼠标沿直线匀速移动了12 cm,耗时1 s,则定位球的角速度为( )
A. rad/s B. rad/s
C.6 rad/s D.12 rad/s
2.某品牌手动榨汁机如图所示,榨汁时手柄绕O点旋转,则手柄上B、C两点的周期、角速度及线速度等物理量的关系是( )
A.TB=TC,vB>vC B.TB=TC,vB
A.齿轮A的角速度比齿轮B的小
B.齿轮A与齿轮B的角速度大小相等
C.齿轮A边缘的线速度比齿轮B边缘的大
D.齿轮A与齿轮B边缘的线速度大小相等
4.(多选)无级变速可在变速范围内任意连续地变换速度,性能优于传统的挡位变速,很多种高档汽车都应用了无级变速。下图是截锥式无级变速模型示意图,两个锥轮之间有一个滚轮,主动轮、滚轮、从动轮之间靠着彼此之间的摩擦力带动。以下判断正确的是( )
A.主动轮转速不变,当位于主动轮与从动轮之间的滚轮从右向左移动时,从动轮转速减小,滚轮从左向右移动时,从动轮转速增大
B.主动轮转速不变,当位于主动轮与从动轮之间的滚轮从左向右移动时,从动轮转速减小,滚轮从右向左移动时,从动轮转速增大
C.当滚轮位于主动轮直径为D1、从动轮直径为D2的位置上时,主动轮转速n1、从动轮转速n2之间的关系为n2=n1
D.当滚轮位于主动轮直径为D1、从动轮直径为D2的位置上时,主动轮转速n1、从动轮转速n2之间的关系为n2=n1
5.下图是教室里的石英钟,设时针、分针长度之比为5∶6,求:
(1)时针、分针的角速度之比与针尖的线速度之比;
(2)从图中位置(2:00)开始计时,时针、分针经过多长时间将第一次重合
6.如图所示的装置可测量子弹的速度,其中薄壁圆筒半径为r,圆筒上的a、b两点是一条直径上的两个端点(图中OO'为圆筒轴线),圆筒以速度v竖直向下匀速运动。若某时刻子弹沿图示平面正好水平射入a点,且恰能经b点穿出。
(1)若圆筒匀速下落时不转动,求子弹射入a点时速度v0的大小;
(2)若圆筒匀速下落的同时绕OO'匀速转动,求圆筒转动的角速度条件。
参考答案:
基础练
1.一个物体以恒定角速度ω做匀速圆周运动时,下列说法正确的是( )
A.轨道半径越大线速度越小
B.轨道半径越大线速度越大
C.轨道半径越大周期越大
D.轨道半径越大周期越小
解析:物体以一定的角速度做匀速圆周运动,由v=ωr得,v与r成正比,所以当半径越大时,线速度也越大,故B正确,A错误;由ω=得,T与ω成反比,与半径无关,因此周期不变,故C、D错误。
答案:B
2.如图所示,一个小球绕圆心O做匀速圆周运动,已知圆周半径为r,该小球运动的角速度为ω,则它运动的线速度大小为( )
A. B.ωr
C.ω2r D.ωr2
解析:小球做匀速圆周运动,转动的半径为r,角速度为ω,故线速度为v=ωr,B正确。
答案:B
3.在一棵大树将要被伐倒的时候,有经验的伐木工人会双眼紧盯着树梢,根据树梢的运动情况来判断大树正在朝哪个方向倒下,从而避免被倒下的大树砸伤,从物理知识的角度来解释,下列说法正确的是( )
A.树木倒下时,树梢的角速度较大,易于判断
B.树木倒下时,树梢的线速度较大,易于判断
C.树木倒下时,树梢的周期较大,易于判断
D.伐木工人的经验没有科学依据
解析:整个大树的角速度和周期相同,树梢的转动半径大,线速度大。
答案:B
4.下图为一种早期的自行车,这种自行车前轮的直径很大,这样的设计在当时主要是为了( )
A.提高速度 B.提高稳定性
C.骑行方便 D.减小阻力
解析:在骑车人脚蹬踏板转速一定的情况下,据公式v=2πrn知,轮子半径越大,车轮边缘的线速度越大,车行驶得也就越快,故A选项正确。
答案:A
5.如图所示,当用扳手拧螺母时,扳手上的P、Q两点的角速度分别为ωP和ωQ,线速度大小分别为vP和vQ,则( )
A.ωP=ωQ,vP
解析:由于P、Q两点属于同轴转动,所以P、Q两点的角速度是相等的,即ωP=ωQ;同时由图可知Q点到螺母的距离比较大,所以Q点的线速度大,即vP
6.做匀速圆周运动的物体,20 s内沿半径为10 m的圆周运动了100 m,试求物体做匀速圆周运动时:
(1)线速度的大小;
(2)角速度的大小;
(3)周期的大小。
解析:(1)依据线速度的定义式可得
v=m/s=5m/s。
(2)依据v=ωr可得
ω=rad/s=0.5rad/s。
(3)T=s=4πs。
答案:(1)5 m/s (2)0.5 rad/s (3)4π s
7.一个圆环以竖直直径AB为轴匀速转动,如图所示。
(1)求环上M、N两点的线速度的大小之比;
(2)求M、N的角速度之比。
解析:M、N是同一环上的两点,它们与环具有相同的角速度,即ωM∶ωN=1∶1,两点做圆周运动的半径之比rM∶rN=sin60°∶sin30°=∶1,故vM∶vN=ωMrM∶ωNrN=∶1。
答案:(1)∶1 (2)1∶1
提升练
1.某品牌的机械鼠标内部结构如图所示,机械鼠标中的定位球的直径是2.0 cm,某次操作中,鼠标沿直线匀速移动了12 cm,耗时1 s,则定位球的角速度为( )
A. rad/s B. rad/s
C.6 rad/s D.12 rad/s
解析:根据线速度定义式得,定位球的线速度为v=cm/s=12cm/s;由角速度与线速度关系v=ωr,得定位球的角速度为ω=rad/s=12rad/s,D正确。
答案:D
2.某品牌手动榨汁机如图所示,榨汁时手柄绕O点旋转,则手柄上B、C两点的周期、角速度及线速度等物理量的关系是( )
A.TB=TC,vB>vC B.TB=TC,vB
3.(多选)明代出版的《天工开物》一书中有牛力齿轮水车图(如图所示),记录了我们祖先的劳动智慧。若A、B两齿轮车半径的大小关系为RA>RB,则( )
A.齿轮A的角速度比齿轮B的小
B.齿轮A与齿轮B的角速度大小相等
C.齿轮A边缘的线速度比齿轮B边缘的大
D.齿轮A与齿轮B边缘的线速度大小相等
解析:齿轮A与齿轮B是同缘传动,边缘点的线速度相等,即vA=vB,根据公式v=ωr可知,半径比较大的齿轮A的角速度小于半径比较小的齿轮B的角速度,即ωA<ωB,故A、D正确,B、C错误。
答案:AD
4.(多选)无级变速可在变速范围内任意连续地变换速度,性能优于传统的挡位变速,很多种高档汽车都应用了无级变速。下图是截锥式无级变速模型示意图,两个锥轮之间有一个滚轮,主动轮、滚轮、从动轮之间靠着彼此之间的摩擦力带动。以下判断正确的是( )
A.主动轮转速不变,当位于主动轮与从动轮之间的滚轮从右向左移动时,从动轮转速减小,滚轮从左向右移动时,从动轮转速增大
B.主动轮转速不变,当位于主动轮与从动轮之间的滚轮从左向右移动时,从动轮转速减小,滚轮从右向左移动时,从动轮转速增大
C.当滚轮位于主动轮直径为D1、从动轮直径为D2的位置上时,主动轮转速n1、从动轮转速n2之间的关系为n2=n1
D.当滚轮位于主动轮直径为D1、从动轮直径为D2的位置上时,主动轮转速n1、从动轮转速n2之间的关系为n2=n1
解析:设某一时刻,滚轮位于主动轮直径为D1、从动轮直径为D2的位置上,三个轮的轮缘的线速度相等,得n1D1=n2D2,即n2=n1,故C选项正确,D选项错误;当位于主动轮与从动轮之间的滚轮从左向右移动时,D1变小,D2变大,在n1不变的情况下,n2变小,反之,当滚轮从右向左移动时,D1变大,D2变小,在n1不变的情况下,n2变大,故B选项正确,A选项错误。
答案:BC
5.下图是教室里的石英钟,设时针、分针长度之比为5∶6,求:
(1)时针、分针的角速度之比与针尖的线速度之比;
(2)从图中位置(2:00)开始计时,时针、分针经过多长时间将第一次重合
解析:(1)时针的周期T1=12h,分针的周期T2=1h
因此ω1∶ω2==1∶12
v1∶v2=ω1r1∶ω2r2=5∶72。
(2)设经过时间t时针、分针第一次重合,则ω2t-ω1t=t=
解得t=h。
答案:(1)1∶12 5∶72 (2) h
6.如图所示的装置可测量子弹的速度,其中薄壁圆筒半径为r,圆筒上的a、b两点是一条直径上的两个端点(图中OO'为圆筒轴线),圆筒以速度v竖直向下匀速运动。若某时刻子弹沿图示平面正好水平射入a点,且恰能经b点穿出。
(1)若圆筒匀速下落时不转动,求子弹射入a点时速度v0的大小;
(2)若圆筒匀速下落的同时绕OO'匀速转动,求圆筒转动的角速度条件。
解析:(1)子弹做平抛运动,水平方向2r=v0t
竖直方向vt=gt2
解得v0=。
(2)圆筒转动的角度是2π的整数倍
2πn=ωt(n=1,2,3,…)
下落时间t=
解得ω=(n=1,2,3,…)。
答案:(1)
(2)ω=(n=1,2,3,…)
