第三章 3.4 3.4.2 基本不等式(二)
文档属性
| 名称 | 第三章 3.4 3.4.2 基本不等式(二) |  | |
| 格式 | zip | ||
| 文件大小 | 254.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-06 08:05:36 | ||
图片预览






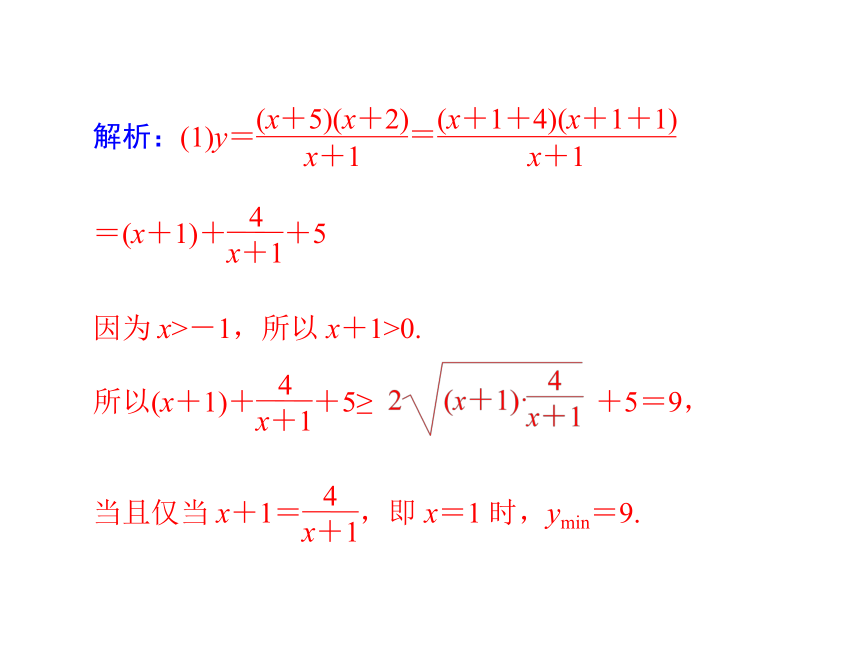
文档简介
(共16张PPT)
3.4.2 基本不等式(二)
1.进一步理解并掌握基本不等式 ≤
a+b
2
及其变形公式.
2.掌握用基本不等式解决一些简单的最值问题.
a+b
1.基本不等式 ≤
2
,成立满足的条件是_____________.
当且仅当________时,等号成立.
a,b 都是正数
a=b
练习1:已知 x>0,若 x+
81
x
的值最小,则 x 为(
)
B
A.81
B.9
C.3
D.16
2.当 a,b 均为正数时,
a=b
(1)a+b≥________,当且仅当_______时,等号成立.
(2)ab≤________,当且仅当______时,等号成立.
练习2:若 a>b>0,则下面不等式正确的是( )
C
练习3:若 x+2y=1,则 2x+4y的最小值是________.
2
a=b
2.(1)当两个正数 a,b,它们的和 a+b 为定值时,ab 有
最小值还是最大值,它是多少?
(2)当两个正数 a,b,它们的乘积 ab 为定值时,a+b 最小
值还是最大值,它是多少?
(2) 已知 x> -1 ,求函数 y = 2
题型1
利用基本不等式求最值
(x+5)(x+2)
x+1
的最小值为
例1:(1)已知 x>-1,求函数 y=
________;
x+1
x +5x+6
(x> -1) 的最大值为
________.
+5
解析:(1)y=
(x+5)(x+2)
x+1
=
(x+1+4)(x+1+1)
x+1
=(x+1)+
4
x+1
因为 x>-1,所以 x+1>0.
所以(x+1)+
4
x+1
+5≥
+5=9,
当且仅当 x+1=
4
x+1
,即 x=1 时,ymin=9.
【变式与拓展】
B
题型2
利用基本不等式整体换元
例2:若正数 a,b 满足 ab=a+b+3,求 ab 及 a+b 的取
值范围.
思维突破:本题主要考查均值不等式在求最值时的运用,
并体现了换元法、构造法等重要思想.
整体思想是分析这类题目的突破口,即a+b
与ab分别是统一的整体,把a+b 转换成ab 或把ab 转换成a
+b.
【变式与拓展】
2.(2010 年浙江)若正实数 x,y,满足 2x+y+6=xy,则
xy 的最小值是________.
18
是“当且仅当 时”;这显然不可能同时成立,因此等号取
易错点评:多次利用基本不等式解题,没有考虑等号能否
同时成立.
在解题过程中先后两次用到了重要不等式,第一次等号成
立的条件是“当且仅当 a=2b 时”;而第二次等号成立的条件
不到.
利用基本不等式求最值及取值范围:
(1)应用基本不等式时,应注意三个条件:“一正、二定、
三相等”.
(2)常用方法:拼凑系数法、整体代换法、换元法、配方法
等.
3.4.2 基本不等式(二)
1.进一步理解并掌握基本不等式 ≤
a+b
2
及其变形公式.
2.掌握用基本不等式解决一些简单的最值问题.
a+b
1.基本不等式 ≤
2
,成立满足的条件是_____________.
当且仅当________时,等号成立.
a,b 都是正数
a=b
练习1:已知 x>0,若 x+
81
x
的值最小,则 x 为(
)
B
A.81
B.9
C.3
D.16
2.当 a,b 均为正数时,
a=b
(1)a+b≥________,当且仅当_______时,等号成立.
(2)ab≤________,当且仅当______时,等号成立.
练习2:若 a>b>0,则下面不等式正确的是( )
C
练习3:若 x+2y=1,则 2x+4y的最小值是________.
2
a=b
2.(1)当两个正数 a,b,它们的和 a+b 为定值时,ab 有
最小值还是最大值,它是多少?
(2)当两个正数 a,b,它们的乘积 ab 为定值时,a+b 最小
值还是最大值,它是多少?
(2) 已知 x> -1 ,求函数 y = 2
题型1
利用基本不等式求最值
(x+5)(x+2)
x+1
的最小值为
例1:(1)已知 x>-1,求函数 y=
________;
x+1
x +5x+6
(x> -1) 的最大值为
________.
+5
解析:(1)y=
(x+5)(x+2)
x+1
=
(x+1+4)(x+1+1)
x+1
=(x+1)+
4
x+1
因为 x>-1,所以 x+1>0.
所以(x+1)+
4
x+1
+5≥
+5=9,
当且仅当 x+1=
4
x+1
,即 x=1 时,ymin=9.
【变式与拓展】
B
题型2
利用基本不等式整体换元
例2:若正数 a,b 满足 ab=a+b+3,求 ab 及 a+b 的取
值范围.
思维突破:本题主要考查均值不等式在求最值时的运用,
并体现了换元法、构造法等重要思想.
整体思想是分析这类题目的突破口,即a+b
与ab分别是统一的整体,把a+b 转换成ab 或把ab 转换成a
+b.
【变式与拓展】
2.(2010 年浙江)若正实数 x,y,满足 2x+y+6=xy,则
xy 的最小值是________.
18
是“当且仅当 时”;这显然不可能同时成立,因此等号取
易错点评:多次利用基本不等式解题,没有考虑等号能否
同时成立.
在解题过程中先后两次用到了重要不等式,第一次等号成
立的条件是“当且仅当 a=2b 时”;而第二次等号成立的条件
不到.
利用基本不等式求最值及取值范围:
(1)应用基本不等式时,应注意三个条件:“一正、二定、
三相等”.
(2)常用方法:拼凑系数法、整体代换法、换元法、配方法
等.
