第三章 3.3 3.3.2 简单的线性规划问题(一)
文档属性
| 名称 | 第三章 3.3 3.3.2 简单的线性规划问题(一) |

|
|
| 格式 | zip | ||
| 文件大小 | 308.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-06 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
3.3.2 简单的线性规划问题(一)
1.了解线性规划的意义,了解线性约束条件、线性目标函
数、可行解、可行域、最优解等基本概念.
2.掌握线性规划问题的图解法,会用图解法求目标函数的
最大值、最小值.
3.训练数形结合、化归等熟悉思想,培养和发展数学应用
意识.
名称 意义
约束条件 关于变量 x,y 的不等式(方程)组
线性约束条件 关于 x,y 的一次不等式(或方程)组成的平面区
域
目标函数 欲求最大值或最小值的关于变量 x,y 的函数解
析式
线性目标函数 关于 x,y 的一次解析式
线性规划相关概念.
名称 意义
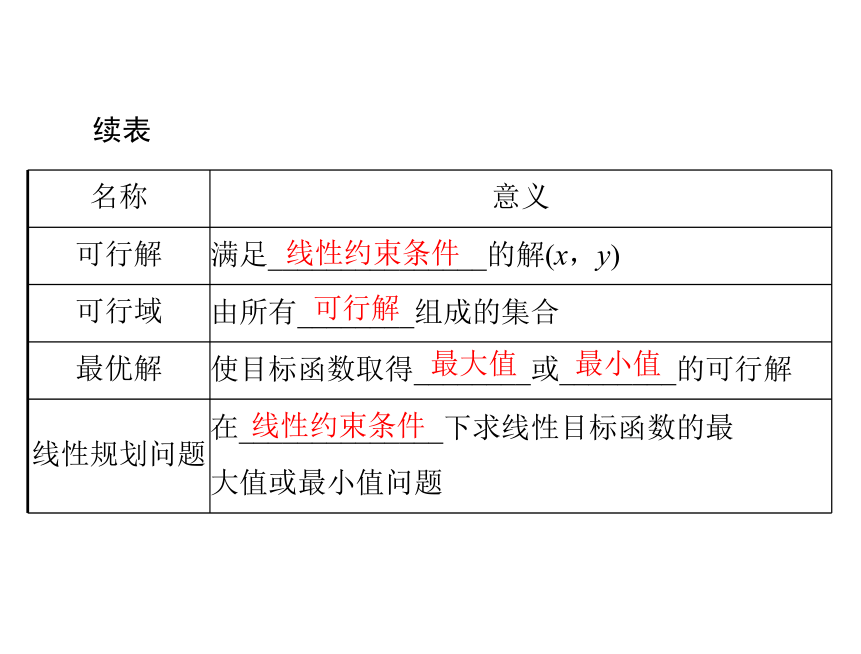
可行解 满足_______________的解(x,y)
可行域 由所有________组成的集合
最优解 使目标函数取得________或________的可行解
线性规划问题 在______________下求线性目标函数的最
大值或最小值问题
续表
线性约束条件
可行解
最大值
最小值
线性约束条件
x-y≥6,
练习1:已知 x,y 满足约束条件 2x+y<9,
分别确定
x≥1,
x,y 的值,使 z=x+3y 取到最大值或最小值,其中__________
为可行域,__________为线性目标函数.
z=x+3y
x≥0,
练习2:已知实数 x,y 满足 y≤1,
求 2x+y 的
x-2y+1≤0,
最大值,这个问题就是______________.满足不等式组的解(x,
y)叫做_______,如
是一组可行解,
由所有可行解组成的集合即不等式组所表
示的平面区域(如图 3-3-1 中阴影部
分)是________.易知,当 x=1,y=1 时,
目标函数 z=2x+y取最大值 3,故(1,1)
是这个规划问题的________.
线性规划问题
可行解
可行域
最优解
图 3-3-1
1.z=x2+y2-3 是线性目标函数吗?
答案:不是,因为 x,y 的系数是 2
2.线性目标函数的最优解只有唯一一个吗?
答案:不是,最优解可能有无数个.
题型1
线性目标函数的最值
x-4y≤-3,
例1:已知变量 x,y满足 3x+5y≤25,
求 z=2x+y 的
x≥1,
最大值和最小值.
思维突破:把z 看成直线在y 轴上的截距,先画出可行域,
再求z 的最值.
自主解答:作出不等式组所表示的可行域,如图 D14.
图 D14
设直线 l0:2x+y=0,直线 l:2x+y=z,则 z 的几何意义
是直线 y=-2x+z 在 y 轴上的截距.
显然,当直线越往上移动时,对应在 y 轴上的截距越大,
即 z 越大;当直线越往下移动时,对应在 y 轴上的截距越小,
即 z 越小.
作一组与直线 l0 平行的直线系 l,上下平移,可得:
当直线 l 移动到直线 l2 时,即过点 A(5,2)时,zmax=2×5+2
=12;
当直线 l 移动到直线 l1 时,即过点 B(1,1)时,zmin=2×1+1
=3.
正确作出可行域后,将目标函数变为直线方程
的斜截式的形式,应注意该直线在y 轴上的截距与目标函数z
取值的关系.再注意该直线的斜率与可行域边界直线的斜率关
系,以便准确找到最优解.
【变式与拓展】
x-2y+4≥0,
1.已知实数 x,y 满足约束条件 2x+y-2≥0,
3x-y-3≤0,
则目标
函数 z=x+2y 的最大值的可行解为________.
(2,3)
x-2≤0,
2.若x,y满足线性约束条件 y-1≤0,
求 z=x+
x+2y-2≥0,
y 的最小值.
解:作出不等式组所表示的可行域如图 D17 中阴影部分.
将 z=x+y 变形为 y=-x+z,这是斜率为-1,随 z 变化
的一组平行线,当直线 y=-x+z 经过可行域内的 A 点时,直
线 y=-x+z 在 y 轴上的截距最小,z 也最小.这里 A 点是直线
x+2y-2=0 与直线 y=1 的交点.
解方程组
x+2y-2=0,
y=1,
得
x=0,
y=1.
此时 z=0+1=1.故 z 的最小值为 1.
图 D17
题型2
线性规划的逆向性问题
y≥1,
例2:已知实数 x,y 满足 y≤2x-1,
x+y≤m,
如果目标函数 z
=x-y 的最小值为-1,则实数 m=(
)
A.7
B.5
C.4
D.3
思维突破:画出x,y 满足的可行域,可得直线y=2x-1
与直线x+y=m 的交点使目标函数z=x-y 取得最小值.
答案:B
【变式与拓展】
3.在如图 3-3-2 所示的可行域内,目标函数 z=x+ay
)
取得最小值的最优解有无数个,则 a 的一个可能值是(
图 3-3-2
A. -3
B.3
C. -1
D.1
解析:分析知“目标函数与直线 BC 重合时 z 最小”,故
D
x-y+5≥0,
4.已知 x,y 满足 x≤3,
x+y+k≥0,
且 z=2x+4y 的最小值
)
为-6,则常数 k=(
A.2
B.9
C.3
D.0
解析:画图后知:当 x=3 时 z=2x+4y 取最小值-6.
D
题型3
线性规划的间接应用
x+2y-19≥0,
例3:设二元一次不等式组 x-y+8≥0,
所表示的平
2x+y-14≤0,
面区域为 M,使函数 y=ax(a>0,a≠1)的图象过区域 M 的 a
)
的取值范围是(
A.[1,3]
C.[2,9]
B.[ 2, ]
D.[ ,9]
思维突破:本题考查线性规划与指数函数.画出平面区域
M,观察图象并结合指数函数性质即可.
解析:如图 D15 中的阴影部分为平面区域 M, 显然,只需
研究过(1,9),(3,8)两种情形.
图 D15
a1≤9 且 a3≥8,即 2≤a≤9.
答案:C
【变式与拓展】
x-y+1≥0,
5.若实数 x,y 满足 x+y≥0,
x≤0,
则 z=3x+2y 的最小值
是(
B
)
A.0
C.
B.1
D.9
例4:若 x,y 满足不等式组
求 z=-3x
-2y 的最值.
试解:作出约束条件表示的可行域,如图 D16 中的阴影部
分,则点 A(10,4),B(3,6).
令 p=3x+2y,
作直线 l:3x+2y=0,
当直线 l 右移过点 B(3,6)时,pmin=21;
当直线 l 继续右移过点 A(10,4)时,pmax=38.
又 z=-p,
故 zmax=-21,zmin=-38.
图 D16
易错点评:直线在y 轴上的截距与目标函数z=-3x-2y
取值的关系上出错.直线ax+by=z 往右(或往左)平移时,z 随
之增大(或减小),只有当a>0 时,才能成立.当a<0 时,可利
用换元将a 变为大于0.
解简单线性规划问题的基本步骤:
(1)画图:画出线性约束条件所表示的平面区域;
(2)定线:令 z=0,得到一过原点的直线;
(3)平移:在线性目标函数所表示的一组平行线中,利用平
移的方法找出与可行域有公共点且截距最大或最小的直线;
(4)求最优解;
(5)求最值.
3.3.2 简单的线性规划问题(一)
1.了解线性规划的意义,了解线性约束条件、线性目标函
数、可行解、可行域、最优解等基本概念.
2.掌握线性规划问题的图解法,会用图解法求目标函数的
最大值、最小值.
3.训练数形结合、化归等熟悉思想,培养和发展数学应用
意识.
名称 意义
约束条件 关于变量 x,y 的不等式(方程)组
线性约束条件 关于 x,y 的一次不等式(或方程)组成的平面区
域
目标函数 欲求最大值或最小值的关于变量 x,y 的函数解
析式
线性目标函数 关于 x,y 的一次解析式
线性规划相关概念.
名称 意义
可行解 满足_______________的解(x,y)
可行域 由所有________组成的集合
最优解 使目标函数取得________或________的可行解
线性规划问题 在______________下求线性目标函数的最
大值或最小值问题
续表
线性约束条件
可行解
最大值
最小值
线性约束条件
x-y≥6,
练习1:已知 x,y 满足约束条件 2x+y<9,
分别确定
x≥1,
x,y 的值,使 z=x+3y 取到最大值或最小值,其中__________
为可行域,__________为线性目标函数.
z=x+3y
x≥0,
练习2:已知实数 x,y 满足 y≤1,
求 2x+y 的
x-2y+1≤0,
最大值,这个问题就是______________.满足不等式组的解(x,
y)叫做_______,如
是一组可行解,
由所有可行解组成的集合即不等式组所表
示的平面区域(如图 3-3-1 中阴影部
分)是________.易知,当 x=1,y=1 时,
目标函数 z=2x+y取最大值 3,故(1,1)
是这个规划问题的________.
线性规划问题
可行解
可行域
最优解
图 3-3-1
1.z=x2+y2-3 是线性目标函数吗?
答案:不是,因为 x,y 的系数是 2
2.线性目标函数的最优解只有唯一一个吗?
答案:不是,最优解可能有无数个.
题型1
线性目标函数的最值
x-4y≤-3,
例1:已知变量 x,y满足 3x+5y≤25,
求 z=2x+y 的
x≥1,
最大值和最小值.
思维突破:把z 看成直线在y 轴上的截距,先画出可行域,
再求z 的最值.
自主解答:作出不等式组所表示的可行域,如图 D14.
图 D14
设直线 l0:2x+y=0,直线 l:2x+y=z,则 z 的几何意义
是直线 y=-2x+z 在 y 轴上的截距.
显然,当直线越往上移动时,对应在 y 轴上的截距越大,
即 z 越大;当直线越往下移动时,对应在 y 轴上的截距越小,
即 z 越小.
作一组与直线 l0 平行的直线系 l,上下平移,可得:
当直线 l 移动到直线 l2 时,即过点 A(5,2)时,zmax=2×5+2
=12;
当直线 l 移动到直线 l1 时,即过点 B(1,1)时,zmin=2×1+1
=3.
正确作出可行域后,将目标函数变为直线方程
的斜截式的形式,应注意该直线在y 轴上的截距与目标函数z
取值的关系.再注意该直线的斜率与可行域边界直线的斜率关
系,以便准确找到最优解.
【变式与拓展】
x-2y+4≥0,
1.已知实数 x,y 满足约束条件 2x+y-2≥0,
3x-y-3≤0,
则目标
函数 z=x+2y 的最大值的可行解为________.
(2,3)
x-2≤0,
2.若x,y满足线性约束条件 y-1≤0,
求 z=x+
x+2y-2≥0,
y 的最小值.
解:作出不等式组所表示的可行域如图 D17 中阴影部分.
将 z=x+y 变形为 y=-x+z,这是斜率为-1,随 z 变化
的一组平行线,当直线 y=-x+z 经过可行域内的 A 点时,直
线 y=-x+z 在 y 轴上的截距最小,z 也最小.这里 A 点是直线
x+2y-2=0 与直线 y=1 的交点.
解方程组
x+2y-2=0,
y=1,
得
x=0,
y=1.
此时 z=0+1=1.故 z 的最小值为 1.
图 D17
题型2
线性规划的逆向性问题
y≥1,
例2:已知实数 x,y 满足 y≤2x-1,
x+y≤m,
如果目标函数 z
=x-y 的最小值为-1,则实数 m=(
)
A.7
B.5
C.4
D.3
思维突破:画出x,y 满足的可行域,可得直线y=2x-1
与直线x+y=m 的交点使目标函数z=x-y 取得最小值.
答案:B
【变式与拓展】
3.在如图 3-3-2 所示的可行域内,目标函数 z=x+ay
)
取得最小值的最优解有无数个,则 a 的一个可能值是(
图 3-3-2
A. -3
B.3
C. -1
D.1
解析:分析知“目标函数与直线 BC 重合时 z 最小”,故
D
x-y+5≥0,
4.已知 x,y 满足 x≤3,
x+y+k≥0,
且 z=2x+4y 的最小值
)
为-6,则常数 k=(
A.2
B.9
C.3
D.0
解析:画图后知:当 x=3 时 z=2x+4y 取最小值-6.
D
题型3
线性规划的间接应用
x+2y-19≥0,
例3:设二元一次不等式组 x-y+8≥0,
所表示的平
2x+y-14≤0,
面区域为 M,使函数 y=ax(a>0,a≠1)的图象过区域 M 的 a
)
的取值范围是(
A.[1,3]
C.[2,9]
B.[ 2, ]
D.[ ,9]
思维突破:本题考查线性规划与指数函数.画出平面区域
M,观察图象并结合指数函数性质即可.
解析:如图 D15 中的阴影部分为平面区域 M, 显然,只需
研究过(1,9),(3,8)两种情形.
图 D15
a1≤9 且 a3≥8,即 2≤a≤9.
答案:C
【变式与拓展】
x-y+1≥0,
5.若实数 x,y 满足 x+y≥0,
x≤0,
则 z=3x+2y 的最小值
是(
B
)
A.0
C.
B.1
D.9
例4:若 x,y 满足不等式组
求 z=-3x
-2y 的最值.
试解:作出约束条件表示的可行域,如图 D16 中的阴影部
分,则点 A(10,4),B(3,6).
令 p=3x+2y,
作直线 l:3x+2y=0,
当直线 l 右移过点 B(3,6)时,pmin=21;
当直线 l 继续右移过点 A(10,4)时,pmax=38.
又 z=-p,
故 zmax=-21,zmin=-38.
图 D16
易错点评:直线在y 轴上的截距与目标函数z=-3x-2y
取值的关系上出错.直线ax+by=z 往右(或往左)平移时,z 随
之增大(或减小),只有当a>0 时,才能成立.当a<0 时,可利
用换元将a 变为大于0.
解简单线性规划问题的基本步骤:
(1)画图:画出线性约束条件所表示的平面区域;
(2)定线:令 z=0,得到一过原点的直线;
(3)平移:在线性目标函数所表示的一组平行线中,利用平
移的方法找出与可行域有公共点且截距最大或最小的直线;
(4)求最优解;
(5)求最值.
