第三章 3.3 3.3.3 简单的线性规划问题(二)
文档属性
| 名称 | 第三章 3.3 3.3.3 简单的线性规划问题(二) |  | |
| 格式 | zip | ||
| 文件大小 | 410.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-06 08:06:44 | ||
图片预览







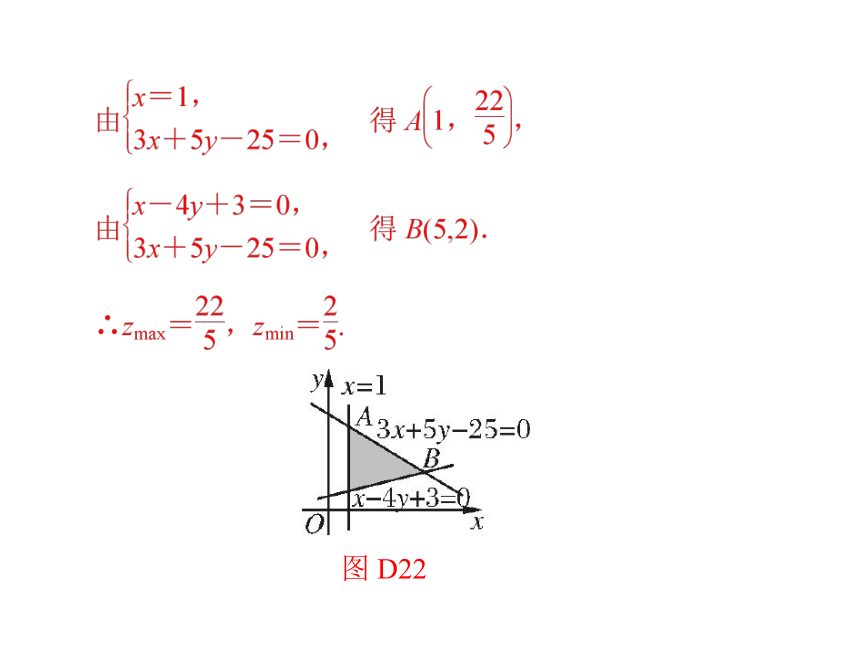
文档简介
(共23张PPT)
3.3.3 简单的线性规划问题(二)
1.进一步了解线性规划的意义,了解线性约束条件、线性
目标函数、可行解、可行域、最优解等基本概念.
2.掌握线性规划问题的图解法,会用图解法求目标函数的
最大值、最小值.
3.训练数形结合、化归等常用思想,培养和发展数学应用
意识.
设 z=— ,求 z
非线性目标函数.
x,y
要求最值中的函数不是关于变量________的一次解析式.
x-4y+3≤0,
练习:变量 x,y 满足 3x+5y-25≤0,
x≥1,
y
x
的最小值和最大值.其中_______为非线性目标函数.
y
x
z=
答案:分别是“斜率型”、“两点间距离型” 、“点到直
线距离型”的目标函数.
(-1,2)
(1,-2)
|3x+4y+5|
(3)
5
表示点 P(x,y)与________________的距离.
直线3x+4y+5=0
(0,0)
(0,0)
题型1
非线性目标函数(斜率)
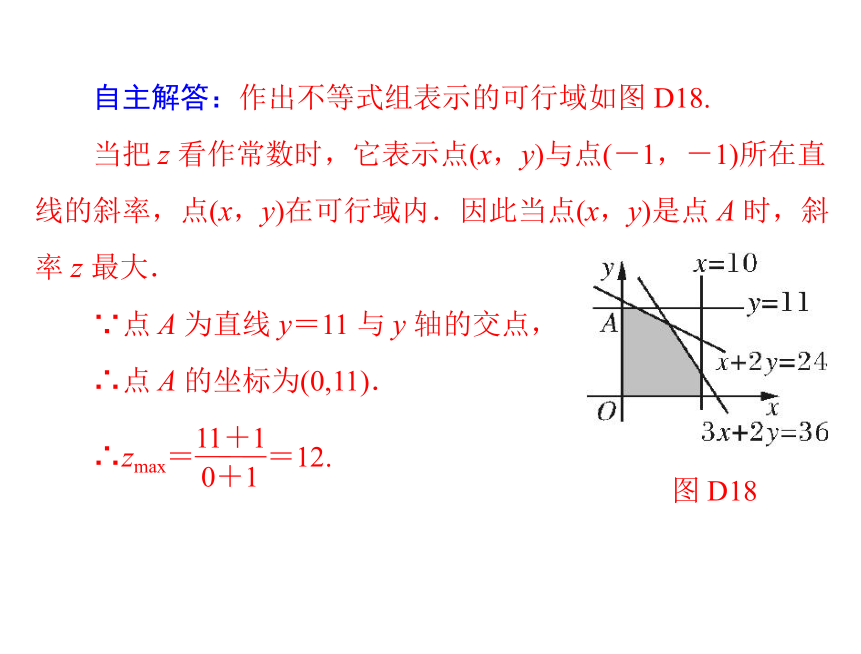
例1:求 z=
y+1
x+1
的最大值,其中 x,y 满足约束条件
思维突破:把所求问题看成区域上的点与点(-1,-1)连
线的斜率.
自主解答:作出不等式组表示的可行域如图 D18.
当把 z 看作常数时,它表示点(x,y)与点(-1,-1)所在直
线的斜率,点(x,y)在可行域内.因此当点(x,y)是点 A 时,斜
率 z 最大.
∵点 A 为直线 y=11 与 y 轴的交点,
∴点 A 的坐标为(0,11).
∴zmax=
11+1
0+1
=12.
图 D18
设 z=—,求 z 的最
【变式与拓展】
x-4y+3≤0,
1.变量 x,y 满足 3x+5y-25≤0,
x≥1,
y
x
小值和最大值.
解:作出可行域,如图 D22,当把 z 看作常数时,它表示
直线 y=zx 的斜率,因此,当直线 y=zx 过点 A 时,z 最大;当
直线 y=zx 过点 B 时,z 最小.
图 D22
x-y≥0,
2.设变量满足约束条件 x+y≥0,
2x+y≤1,
则
y
x+1
的最大值是
(
)
B
题型2
非线性目标函数(距离)
自主解答:作出不等式组所表示的可行域如图 D19.
把 z 当作常数时,它表示点(x,y)到点(0,-1)的距离,点(x,
y)在可行域内.由图 D19 可知:z 的最小值为点(0,-1)到直线
2x+5y=15 的距离.
图 D19
对形如z=(x-a)2+(y-b)2 的目标函数可化为
可行域内的点(x,y)与点(a,b)间的距离的最值的问题.
【变式与拓展】
A
2x+5y≥10,
4.已知 x,y 满足约束条件 2x-3y≥-6,
2x+y≤10,
则 z=x2+y2
的最小值为____________.
100
29
题型3
非线性目标函数(面积)
图 D20
答案:D
【变式与拓展】
5.在直角坐标平面上,不等式组
y≥2|x|-1,
y≤x+1
所表示的
平面区域的面积为(
)
B
解析:作出不等式表示的平面区域即可.
x+y≤5,
6.求由约束条件 2x+y≤6,
确定的平面区域的面积 S
x≥0,y≥0
和周长 C.
图D23,
其四个顶点为 O(0,0),B(3,0),A(0,5),P(1,4).
过点 P 作 y 轴的垂线,垂足为点 C.
则 AC=|5-4|=1,PC=|1-0|=1,
解:由约束条件作出其所确定的平面区域(阴影部分),如
图D23
图 D21
答案:A
易错点评:直线在y轴上的截距与目标函数y=kx+—取值
4
3
的关系上出错.没有正确的思维,同顶点,同高是关键.
1.求目标函数的最值时,要确定目标函数是线性的还是非
线性的.
2.计算非线性目标函数的最值,常借助其几何意义,运用
线性规划的知识解决,计算量小,且直观形象.
3.3.3 简单的线性规划问题(二)
1.进一步了解线性规划的意义,了解线性约束条件、线性
目标函数、可行解、可行域、最优解等基本概念.
2.掌握线性规划问题的图解法,会用图解法求目标函数的
最大值、最小值.
3.训练数形结合、化归等常用思想,培养和发展数学应用
意识.
设 z=— ,求 z
非线性目标函数.
x,y
要求最值中的函数不是关于变量________的一次解析式.
x-4y+3≤0,
练习:变量 x,y 满足 3x+5y-25≤0,
x≥1,
y
x
的最小值和最大值.其中_______为非线性目标函数.
y
x
z=
答案:分别是“斜率型”、“两点间距离型” 、“点到直
线距离型”的目标函数.
(-1,2)
(1,-2)
|3x+4y+5|
(3)
5
表示点 P(x,y)与________________的距离.
直线3x+4y+5=0
(0,0)
(0,0)
题型1
非线性目标函数(斜率)
例1:求 z=
y+1
x+1
的最大值,其中 x,y 满足约束条件
思维突破:把所求问题看成区域上的点与点(-1,-1)连
线的斜率.
自主解答:作出不等式组表示的可行域如图 D18.
当把 z 看作常数时,它表示点(x,y)与点(-1,-1)所在直
线的斜率,点(x,y)在可行域内.因此当点(x,y)是点 A 时,斜
率 z 最大.
∵点 A 为直线 y=11 与 y 轴的交点,
∴点 A 的坐标为(0,11).
∴zmax=
11+1
0+1
=12.
图 D18
设 z=—,求 z 的最
【变式与拓展】
x-4y+3≤0,
1.变量 x,y 满足 3x+5y-25≤0,
x≥1,
y
x
小值和最大值.
解:作出可行域,如图 D22,当把 z 看作常数时,它表示
直线 y=zx 的斜率,因此,当直线 y=zx 过点 A 时,z 最大;当
直线 y=zx 过点 B 时,z 最小.
图 D22
x-y≥0,
2.设变量满足约束条件 x+y≥0,
2x+y≤1,
则
y
x+1
的最大值是
(
)
B
题型2
非线性目标函数(距离)
自主解答:作出不等式组所表示的可行域如图 D19.
把 z 当作常数时,它表示点(x,y)到点(0,-1)的距离,点(x,
y)在可行域内.由图 D19 可知:z 的最小值为点(0,-1)到直线
2x+5y=15 的距离.
图 D19
对形如z=(x-a)2+(y-b)2 的目标函数可化为
可行域内的点(x,y)与点(a,b)间的距离的最值的问题.
【变式与拓展】
A
2x+5y≥10,
4.已知 x,y 满足约束条件 2x-3y≥-6,
2x+y≤10,
则 z=x2+y2
的最小值为____________.
100
29
题型3
非线性目标函数(面积)
图 D20
答案:D
【变式与拓展】
5.在直角坐标平面上,不等式组
y≥2|x|-1,
y≤x+1
所表示的
平面区域的面积为(
)
B
解析:作出不等式表示的平面区域即可.
x+y≤5,
6.求由约束条件 2x+y≤6,
确定的平面区域的面积 S
x≥0,y≥0
和周长 C.
图D23,
其四个顶点为 O(0,0),B(3,0),A(0,5),P(1,4).
过点 P 作 y 轴的垂线,垂足为点 C.
则 AC=|5-4|=1,PC=|1-0|=1,
解:由约束条件作出其所确定的平面区域(阴影部分),如
图D23
图 D21
答案:A
易错点评:直线在y轴上的截距与目标函数y=kx+—取值
4
3
的关系上出错.没有正确的思维,同顶点,同高是关键.
1.求目标函数的最值时,要确定目标函数是线性的还是非
线性的.
2.计算非线性目标函数的最值,常借助其几何意义,运用
线性规划的知识解决,计算量小,且直观形象.
