第三章 3.3 3.3.4 简单线性规划问题的实际应用
文档属性
| 名称 | 第三章 3.3 3.3.4 简单线性规划问题的实际应用 |

|
|
| 格式 | zip | ||
| 文件大小 | 388.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-06 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
3.3.4 简单线性规划问题的实际应用
1.从实际情境中抽象出简单的线性规划问题,建立数学模型.
2.掌握线性规划问题的图解法,并能应用它解决一些简单的
实际问题.
线性规划的理论和方法主要用于解决以下两类问题:一是在
人力、物力、资金等资源一定的条件下,如何使用它们来完成最
多的任务;二是给定一项任务,如何合理安排和规划,能以最少
的人力、财力、物力、资金等资源来完成该项任务.
线性规划解应用题的一般步骤.
(1)设出____________;
x,y,z
约束条件
目标函数
(2)列出________,确定________;
(3)画出________;
(4)作目标函数表示的一族平行直线,使其中某条直线与
________有交点,且使其截距最大或最小;
可行域
(5)判断________,求出目标函数的______,并回到原问题
中作答.
最优解
最值
可行域
练习1:有5 辆 6 吨的汽车,4 辆 4 吨的汽车,要运送最多
的货物,完成这项运输任务的线性目标函数为___________.
x≥1,
练习2:已知变量 x,y 满足 y≤2,
x-y≤0,
则 x+y 的最小
)
值是(
A.4
C.2
B.3
D.1
z=6x+4y
C
1.简单线性规划在实际生产生活中主要解决哪些问题?
答案:简单的线性规划在实际生产生活中应用非常广泛,
主要解决的问题是:在资源的限制下,如何使用资源来完成最
多的生产任务;或是给定一项任务,如何合理安排和规划,能
以最少的资源来完成如常见的任务安排问题、配料问题、下料
问题、布局问题、库存问题,通常解法是将实际问题转化为数
学模型,归结为线性规划,使用图解法解决.
2.应用线性规划的图解方法,应具备哪些条件?
(3)确定线性目标函数 z=f(x,y);
(4)画出可行域(即各约束条件所示区域的公共区域);
(5)利用线性目标函数作平行直线系 f(x,y)=t(t 为参数);
(6)观察图形,找到直线 f(x,y)=t 在可行域上使 t 取得欲求
最值的位置,以确定最优解,给出答案.
答案:线性规划问题一般用图解法,其步骤如下:
(1)根据题意,设出变量 x,y;
(2)找出线性约束条件;
题型1
资源配置问题
例1:某工艺品加工厂准备生产具有收藏价值的奥运会标志
——“中国印·舞动的北京”和奥运会吉祥物——“福娃”.该厂
所用的主要原料为 A,B 两种贵重金属,已知生产一套奥运会标志
需用原料 A 和原料 B 的量分别为 4 盒和 3 盒,生产一套奥运会吉
祥物需用原料 A 和原料 B 的量分别为 5 盒和 10 盒.若奥运会标志
每套可获利 700 元,奥运会吉祥物每套可获利 1 200 元,该厂月初
一次性购进原料 A,B 的量分别为 200 盒和 300 盒.问该厂生产奥
运会标志和奥运会吉祥物各多少套才能使该厂月利润最大,最大
利润为多少?
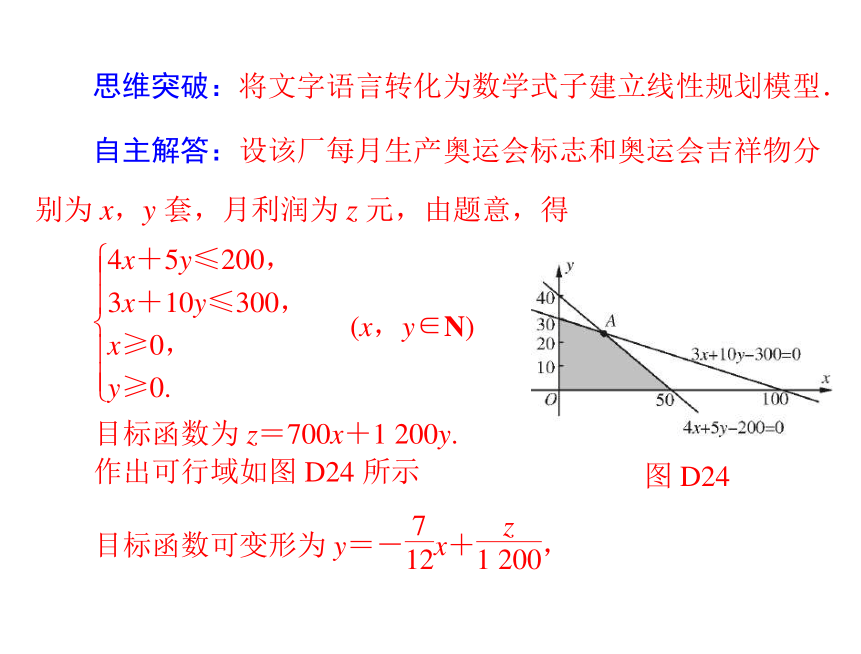
思维突破:将文字语言转化为数学式子建立线性规划模型.
图 D24
自主解答:设该厂每月生产奥运会标志和奥运会吉祥物分
别为 x,y 套,月利润为 z 元,由题意,得
将点 A(20,24)代入 z=700x+1 200y,
得 zmax=700×20+1 200×24=42 800 元
答:当该厂生产奥运会标志和吉祥物分别为 20,24 套时,
月利润最大,最大利润为 42 800 元.
解线性规划应用题时,先转化为简单的线性规
划问题,再按如下步骤完成:①作图:画出约束条件所确定的
平面区域和目标函数所表示的平行直线系中的一条直线 l;②平
移:将直线 l 平行移动,以确定最优解的对应点 A 的位置;③
求值:解有关方程组求出点 A 坐标(即最优解),代入目标函数,
即可求出最值.
混合 烹调 包装
A 1 5 3
B 2 4 1
【变式与拓展】
1.某糖果厂生产 A,B 两种糖果,A 种糖果每箱获利润 40
元,B 种糖果每箱获利润 50 元,其生产过程分为混合、烹调、
包装三道工序,下表为每箱糖果生产过程中所需平均时间(单
位:分钟).
每种糖果的生产过程中,混合的设备至多能用 12 小时,烹
调的设备至多只能用机 30 小时,包装的设备只能用 15 小时,
试求每种糖果各生产多少箱可获得最大利润.
求目标函数 z=40x+50y 的最大值,
作出可行域(如图 D28),其边界 OA:y=0,
AB:3x+y-900=0,BC:5x+4y-1 800=0,
CD:x+2y-720=0,DO:x=0.
图 D28
产品
原料 产品 A 产品 B 产品 C
燃料甲/吨 10 7 5
燃料乙/吨 5 9 13
题型2
降低资源消耗问题
例2:某工厂利用两种燃料生产三种不同的产品 A,B,C,
每消耗一吨燃料与产品 A,B,C 有下列关系:
现知每吨燃料甲与燃料乙的价格之比为 2∶3,现需要三种
产品 A,B,C 各 50 吨,63 吨,65 吨.问如何使用两种燃料,
才能使该厂成本最低?
思维突破:由于该厂成本与两种燃料使用量有关,而产品
A,B,C 又与这两种燃料有关,且这三种产品的产量也有限制,
因此这是一道求线性目标函数在线性约束条件下的最小值问
题,这类简单的线性规划问题一般都可以利用二元一次不等式
组求在可行域上的最优解.
自主解答:设该厂使用燃料甲 x 吨,燃料乙 y 吨,甲每吨
2t 元,则乙每吨为 3t 元.
则成本为 z=2tx+3ty=t(2x+3y).因此只需求 2x+3y 的最
小值即可.
10x+5y≥50,
又由题意,可得 x,y 满足条件 7x+9y≥63,
5x+13y≥65.
作出不等式组所表示的平面区域(如图 D25).
图 D25
【变式与拓展】
2.医院用甲、乙两种原料为手术后的病人配营养餐,甲种
原料每 10 g 含 5 个单位蛋白质和 10 个单位铁质,售价 3 元;
乙种原料每 10 g 含 7 个单位蛋白质和 4 个单位铁质,售价 2 元.
若病人每餐至少需要 35 个单位蛋白质和 40 个单位铁质.试问:
应如何使用甲、乙原料,才能既满足营养,又使费用最省?
图 D29
题型3
整数解处理
例3:某公司每天至少要运送 180 t 货物.公司有 8 辆载重
为 6 t 的 A 型卡车和 4 辆载重为 10 t 的 B 型卡车,A 型卡车每天
可往返 4 次,B 型卡车可往返 3 次,A 型卡车每天花费 320 元,
B 型卡车每天花费 504 元,问如何调配车辆才能使公司每天花
费最少.
思维突破:设A型卡车x 辆,B 型卡车y 辆.问题转化为
线性规划问题.同时应注意到题中的x,y只能取整数.
自主解答:设 A 型卡车 x 辆,B 型卡车 y 辆,则
0≤x≤8,
0≤y≤4,
24x+30y≥180,
0≤x≤8,
即 0≤y≤4,
4x+5y≥30,
目标函数 z=320x+504y.作如图 D26 所示的可行域,
图 D26
做直线 l′:320x+504y=0.在可行域中打上网格,找出(8 ,
0),(8 , 1),(8 , 2),(7 , 1),(7 , 2),(7 , 3),…等整数点.作直
线 l:320x+504y=t 与直线 l′平行,可见当直线 l 过点(8, 0)
时,t 最小,即 zmin=8×320=2 560(元).
根据已知条件写出不等式组是做题的第一步;
第二步画出可行域;第三步找出最优解.其中最困难的是第二
步.
整数解的线性规划问题.如果取最小值时不是整数点,则
考虑此点附近的整数点.
例4:某沙漠地带,考察车每天行驶 200 千米,每辆考察
车可以装载供行驶 14 天的汽油.现有 5 辆考察车,同时从驻地
A 出发,计划完成任务后,再沿原路返回驻地,为了让其中 3
辆车尽可能向更远的地方进行考察(然后再一起返回),甲、乙
两车行至 B 处后,仅留足自己返回驻所必需的汽油,将多余的
汽油供给另外 3 辆使用,问:其他 3 辆可以行进的最远路是多
少千米?
试解:设考察行至B 处用了x天,从B处到最远处用了y
天,则有 2[3(x+y)+2x]≤14×5,
即 5x+3y≤35,且 x>0,y>0.
同时从其余 3 辆车的载油量考虑,
14×5-(5+2)x≤14×3,即 x≥4.
5x+3y≤35,
下求 z=x+y
于是问题转化为在约束条件 x≥4,
y>0
的最大值.
作可行域(如图 D27),则 M(4,5),
图 D27
作直线 l:x+y=0,向右平移过点 M 时,zmax=9.
∴最远路程为 200×(4+5)=1 800(千米).
易错点评:对线性的约束条件考虑不清不全,没考虑甲、
乙两车供油后,自己还须返回这一条件,导致约束条件出错.
1.线性规划的两类重要实际问题的解题思路:
(1)应准确建立数学模型,即根据题意找出约束条件,确定
线性目标函数.
(2)用图解法求得数学模型的解,即画出可行域,在可行域
内求得使目标函数取最值的解.
(3)还要根据实际意义将数学模型的解转化为实际问题的
解,即结合实际情况求得最优解.
2.应用线性规划处理实际问题时应注意的问题:
(1)在求解实际问题时,除严格遵循线性规划求目标函数最
值的方法外,还应考虑实际意义的约束,要认真解读题意,仔
细推敲并挖掘相关条件,同时还应具备批判性检验思维,以保
证解决问题的准确和完美.
(2)在处理实际问题时,x≥0,y≥0 常被忽略,在解题中应
注意.
(3)在求解最优解时,一般采用图解法求解.
3.3.4 简单线性规划问题的实际应用
1.从实际情境中抽象出简单的线性规划问题,建立数学模型.
2.掌握线性规划问题的图解法,并能应用它解决一些简单的
实际问题.
线性规划的理论和方法主要用于解决以下两类问题:一是在
人力、物力、资金等资源一定的条件下,如何使用它们来完成最
多的任务;二是给定一项任务,如何合理安排和规划,能以最少
的人力、财力、物力、资金等资源来完成该项任务.
线性规划解应用题的一般步骤.
(1)设出____________;
x,y,z
约束条件
目标函数
(2)列出________,确定________;
(3)画出________;
(4)作目标函数表示的一族平行直线,使其中某条直线与
________有交点,且使其截距最大或最小;
可行域
(5)判断________,求出目标函数的______,并回到原问题
中作答.
最优解
最值
可行域
练习1:有5 辆 6 吨的汽车,4 辆 4 吨的汽车,要运送最多
的货物,完成这项运输任务的线性目标函数为___________.
x≥1,
练习2:已知变量 x,y 满足 y≤2,
x-y≤0,
则 x+y 的最小
)
值是(
A.4
C.2
B.3
D.1
z=6x+4y
C
1.简单线性规划在实际生产生活中主要解决哪些问题?
答案:简单的线性规划在实际生产生活中应用非常广泛,
主要解决的问题是:在资源的限制下,如何使用资源来完成最
多的生产任务;或是给定一项任务,如何合理安排和规划,能
以最少的资源来完成如常见的任务安排问题、配料问题、下料
问题、布局问题、库存问题,通常解法是将实际问题转化为数
学模型,归结为线性规划,使用图解法解决.
2.应用线性规划的图解方法,应具备哪些条件?
(3)确定线性目标函数 z=f(x,y);
(4)画出可行域(即各约束条件所示区域的公共区域);
(5)利用线性目标函数作平行直线系 f(x,y)=t(t 为参数);
(6)观察图形,找到直线 f(x,y)=t 在可行域上使 t 取得欲求
最值的位置,以确定最优解,给出答案.
答案:线性规划问题一般用图解法,其步骤如下:
(1)根据题意,设出变量 x,y;
(2)找出线性约束条件;
题型1
资源配置问题
例1:某工艺品加工厂准备生产具有收藏价值的奥运会标志
——“中国印·舞动的北京”和奥运会吉祥物——“福娃”.该厂
所用的主要原料为 A,B 两种贵重金属,已知生产一套奥运会标志
需用原料 A 和原料 B 的量分别为 4 盒和 3 盒,生产一套奥运会吉
祥物需用原料 A 和原料 B 的量分别为 5 盒和 10 盒.若奥运会标志
每套可获利 700 元,奥运会吉祥物每套可获利 1 200 元,该厂月初
一次性购进原料 A,B 的量分别为 200 盒和 300 盒.问该厂生产奥
运会标志和奥运会吉祥物各多少套才能使该厂月利润最大,最大
利润为多少?
思维突破:将文字语言转化为数学式子建立线性规划模型.
图 D24
自主解答:设该厂每月生产奥运会标志和奥运会吉祥物分
别为 x,y 套,月利润为 z 元,由题意,得
将点 A(20,24)代入 z=700x+1 200y,
得 zmax=700×20+1 200×24=42 800 元
答:当该厂生产奥运会标志和吉祥物分别为 20,24 套时,
月利润最大,最大利润为 42 800 元.
解线性规划应用题时,先转化为简单的线性规
划问题,再按如下步骤完成:①作图:画出约束条件所确定的
平面区域和目标函数所表示的平行直线系中的一条直线 l;②平
移:将直线 l 平行移动,以确定最优解的对应点 A 的位置;③
求值:解有关方程组求出点 A 坐标(即最优解),代入目标函数,
即可求出最值.
混合 烹调 包装
A 1 5 3
B 2 4 1
【变式与拓展】
1.某糖果厂生产 A,B 两种糖果,A 种糖果每箱获利润 40
元,B 种糖果每箱获利润 50 元,其生产过程分为混合、烹调、
包装三道工序,下表为每箱糖果生产过程中所需平均时间(单
位:分钟).
每种糖果的生产过程中,混合的设备至多能用 12 小时,烹
调的设备至多只能用机 30 小时,包装的设备只能用 15 小时,
试求每种糖果各生产多少箱可获得最大利润.
求目标函数 z=40x+50y 的最大值,
作出可行域(如图 D28),其边界 OA:y=0,
AB:3x+y-900=0,BC:5x+4y-1 800=0,
CD:x+2y-720=0,DO:x=0.
图 D28
产品
原料 产品 A 产品 B 产品 C
燃料甲/吨 10 7 5
燃料乙/吨 5 9 13
题型2
降低资源消耗问题
例2:某工厂利用两种燃料生产三种不同的产品 A,B,C,
每消耗一吨燃料与产品 A,B,C 有下列关系:
现知每吨燃料甲与燃料乙的价格之比为 2∶3,现需要三种
产品 A,B,C 各 50 吨,63 吨,65 吨.问如何使用两种燃料,
才能使该厂成本最低?
思维突破:由于该厂成本与两种燃料使用量有关,而产品
A,B,C 又与这两种燃料有关,且这三种产品的产量也有限制,
因此这是一道求线性目标函数在线性约束条件下的最小值问
题,这类简单的线性规划问题一般都可以利用二元一次不等式
组求在可行域上的最优解.
自主解答:设该厂使用燃料甲 x 吨,燃料乙 y 吨,甲每吨
2t 元,则乙每吨为 3t 元.
则成本为 z=2tx+3ty=t(2x+3y).因此只需求 2x+3y 的最
小值即可.
10x+5y≥50,
又由题意,可得 x,y 满足条件 7x+9y≥63,
5x+13y≥65.
作出不等式组所表示的平面区域(如图 D25).
图 D25
【变式与拓展】
2.医院用甲、乙两种原料为手术后的病人配营养餐,甲种
原料每 10 g 含 5 个单位蛋白质和 10 个单位铁质,售价 3 元;
乙种原料每 10 g 含 7 个单位蛋白质和 4 个单位铁质,售价 2 元.
若病人每餐至少需要 35 个单位蛋白质和 40 个单位铁质.试问:
应如何使用甲、乙原料,才能既满足营养,又使费用最省?
图 D29
题型3
整数解处理
例3:某公司每天至少要运送 180 t 货物.公司有 8 辆载重
为 6 t 的 A 型卡车和 4 辆载重为 10 t 的 B 型卡车,A 型卡车每天
可往返 4 次,B 型卡车可往返 3 次,A 型卡车每天花费 320 元,
B 型卡车每天花费 504 元,问如何调配车辆才能使公司每天花
费最少.
思维突破:设A型卡车x 辆,B 型卡车y 辆.问题转化为
线性规划问题.同时应注意到题中的x,y只能取整数.
自主解答:设 A 型卡车 x 辆,B 型卡车 y 辆,则
0≤x≤8,
0≤y≤4,
24x+30y≥180,
0≤x≤8,
即 0≤y≤4,
4x+5y≥30,
目标函数 z=320x+504y.作如图 D26 所示的可行域,
图 D26
做直线 l′:320x+504y=0.在可行域中打上网格,找出(8 ,
0),(8 , 1),(8 , 2),(7 , 1),(7 , 2),(7 , 3),…等整数点.作直
线 l:320x+504y=t 与直线 l′平行,可见当直线 l 过点(8, 0)
时,t 最小,即 zmin=8×320=2 560(元).
根据已知条件写出不等式组是做题的第一步;
第二步画出可行域;第三步找出最优解.其中最困难的是第二
步.
整数解的线性规划问题.如果取最小值时不是整数点,则
考虑此点附近的整数点.
例4:某沙漠地带,考察车每天行驶 200 千米,每辆考察
车可以装载供行驶 14 天的汽油.现有 5 辆考察车,同时从驻地
A 出发,计划完成任务后,再沿原路返回驻地,为了让其中 3
辆车尽可能向更远的地方进行考察(然后再一起返回),甲、乙
两车行至 B 处后,仅留足自己返回驻所必需的汽油,将多余的
汽油供给另外 3 辆使用,问:其他 3 辆可以行进的最远路是多
少千米?
试解:设考察行至B 处用了x天,从B处到最远处用了y
天,则有 2[3(x+y)+2x]≤14×5,
即 5x+3y≤35,且 x>0,y>0.
同时从其余 3 辆车的载油量考虑,
14×5-(5+2)x≤14×3,即 x≥4.
5x+3y≤35,
下求 z=x+y
于是问题转化为在约束条件 x≥4,
y>0
的最大值.
作可行域(如图 D27),则 M(4,5),
图 D27
作直线 l:x+y=0,向右平移过点 M 时,zmax=9.
∴最远路程为 200×(4+5)=1 800(千米).
易错点评:对线性的约束条件考虑不清不全,没考虑甲、
乙两车供油后,自己还须返回这一条件,导致约束条件出错.
1.线性规划的两类重要实际问题的解题思路:
(1)应准确建立数学模型,即根据题意找出约束条件,确定
线性目标函数.
(2)用图解法求得数学模型的解,即画出可行域,在可行域
内求得使目标函数取最值的解.
(3)还要根据实际意义将数学模型的解转化为实际问题的
解,即结合实际情况求得最优解.
2.应用线性规划处理实际问题时应注意的问题:
(1)在求解实际问题时,除严格遵循线性规划求目标函数最
值的方法外,还应考虑实际意义的约束,要认真解读题意,仔
细推敲并挖掘相关条件,同时还应具备批判性检验思维,以保
证解决问题的准确和完美.
(2)在处理实际问题时,x≥0,y≥0 常被忽略,在解题中应
注意.
(3)在求解最优解时,一般采用图解法求解.
