第三章 3.4 3.4.3 基本不等式的实际应用
文档属性
| 名称 | 第三章 3.4 3.4.3 基本不等式的实际应用 |

|
|
| 格式 | zip | ||
| 文件大小 | 350.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-06 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
3.4.3 基本不等式的实际应用
2.熟练理解并应用基本不等式解决一些简单的应用问题.
1.已知 x,y 都是正数,
(1)如果积 xy 是定值 P,那么当 x=y 时,和________有最
小值________.
x+y
(2)如果和 x+y 是定值 S,那么当 x=y 时,积______有最
小值________.
xy
S2
4
练习1:已知 a>0,b>0,若 ab=9,则 a+b 有最小值为
______;若 a+b=4,则 ab 有最大值为_____.
6
4
1
x
当 x<0 时,ymax=________.
2
-2
练习2:已知函数y=x+—,当x>0时,ymin=________,
1.你是设计师!春天到了,学校决定用篱笆围一个面积为
100 平方米的花圃种花.有以下两种方案:
圆形花圃:造价 12 元/米;矩形花圃:造价 10 元/米;
你觉得哪个方案更省钱呢?
2.在问题 1 中,假若现在只有 36 米的篱笆可用,怎么样
设计才能使得矩形花圃的面积最大?
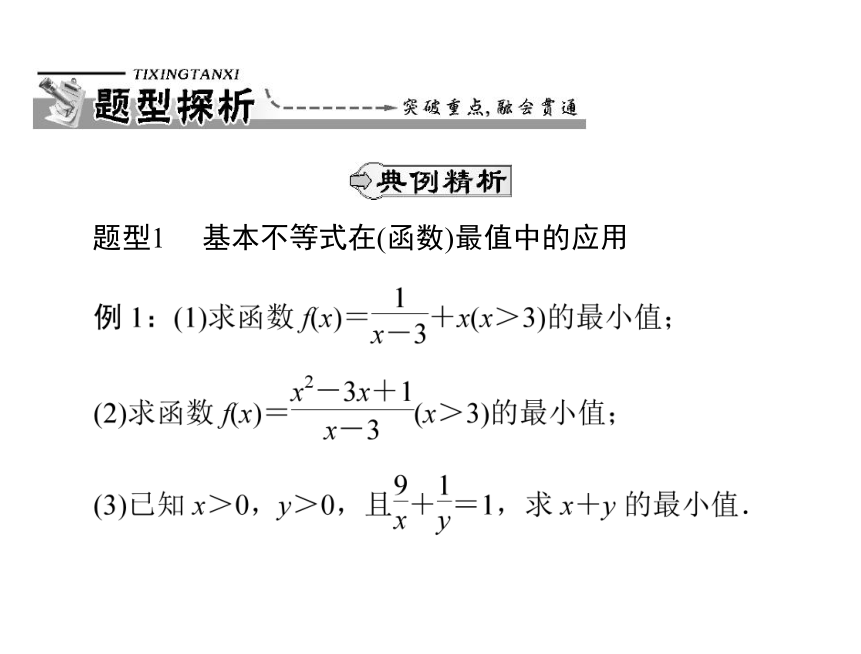
题型1
基本不等式在(函数)最值中的应用
【变式与拓展】
题型2
利用基本不等式进行优化设计(最大值问题)
例2:某村计划建造一个室内面积为 800 m2 的矩形蔬菜温
室.在温室内,沿左、右两侧与后侧内墙各保留 1 m 宽的通道,
沿前侧内墙保留 3 m 宽的空地.当矩形温室的边长各为多少
时?蔬菜的种植面积最大,最大种植面积是多少?
自主解答:设矩形温室的左侧边长为 a m,后侧边长为 b m,
则 ab=800.
蔬菜的种植面积
S=(a-4)(b-2)=ab-4b-2a+8=808-2(a+2b).
所以 S≤808-4 =648(m2).
当 a=2b,即 a=40(m),b=20(m)时,S最大值=648(m2).
答:当矩形温室的左侧边长为 40 m,后侧边长为 20 m 时,
蔬菜的种植面积最大,最大种植面积为 648 m2.
【变式与拓展】
2.某单位用 2 160 万元购得一块空地,计划在该地块上建
造一栋至少 10 层,每层 2 000 平方米的楼房.经测算,如果将
楼房建为 x(x≥10) 层,则每平方米的平均建筑费用为 560 +
48x(单位:元).为了使楼房每平方米的平均综合费用最少,则
)
B
楼房应建为(
A.10 层
C.20 层
B.15 层
D.30 层
题型3
利用基本不等式进行优化设计(最小值问题)
例3:为迎接北京奥运会,北京市决定在首都国际机场粘
贴一幅“福娃”宣传画,如图 3-4-1 要求画面面积为 72 m2,
左、右各留 1 米,上、下各留 0.5 米,问怎样设计画面的长和
宽才能使宣传画所用纸张面积最小?
图 3-4-1
自主解答:设宣传画的长、宽分别为 x,y 米,则 xy=72,
设纸张面积为 S,则:
S=(x+2)(y+1)=xy+x+2y+2
由 xy=72,即 y=
72
x
代入上式,
得 S=74+x+
144
x
≥74+2
=98,
当且仅当 x=
144
x
,即 x=12 时,Smin=98.
所以宣传画的长为 12 米,宽为 6 米,所用纸张面积最小.
【变式与拓展】
3.设计一幅宣传画,要求画面面积 4 840 cm2,画面的上、
下各留 8 cm 的空白,左右各留 5 cm 的空白.怎样确定画面的
高与宽的尺寸,能使宣传画所用纸张最小?
(2)修1m旧墙的费用是—元;
(3)拆去1m旧墙,用所得的材料建1m新墙的费用为—元.
例4:某工厂有旧墙 14 m,现准备利用这面旧墙建造平面
图形为矩形,面积为 126 m2 的厂房,工程条件是:
(1)建 1 m 新墙的费用为 a 元;
a
4
a
2
经讨论有两种方案:
(1)利用旧墙的一段 x m(x<14)为矩形厂房的一面的边长;
(2)矩形一面的边长 x≥14 m.
问如何利用旧墙,即 x 为多少时建墙费用最省?
易错点评:在实际问题中,没有考虑“等号”是否成立,
以至出错.此题是生活实际中常碰到的,有实际意义,综合分
析能力很强,尤其(2)x≥14,往往容易疏忽,不加以考虑,仅以
(1)分析,利用部分旧墙,拆除部分旧墙,用拆得的材料建新墙,
其余的建新墙,虽然结果正确,但没有与(2)作比较,不能算是
一种完整的解法.
1.不等式的应用问题大都与函数相关联,在求最值时,基
本不等式是经常使用的工具,但若对自变量有限制,一定要注
意等号能否取得,若取不到,则必须利用函数的单调性去求函
数的最值.
2.解答不等式应用题的一般步骤:
(1)阅读并理解材料;
(2)建立数学模型;
(3)讨论不等关系;
(4)作出结论.
3.4.3 基本不等式的实际应用
2.熟练理解并应用基本不等式解决一些简单的应用问题.
1.已知 x,y 都是正数,
(1)如果积 xy 是定值 P,那么当 x=y 时,和________有最
小值________.
x+y
(2)如果和 x+y 是定值 S,那么当 x=y 时,积______有最
小值________.
xy
S2
4
练习1:已知 a>0,b>0,若 ab=9,则 a+b 有最小值为
______;若 a+b=4,则 ab 有最大值为_____.
6
4
1
x
当 x<0 时,ymax=________.
2
-2
练习2:已知函数y=x+—,当x>0时,ymin=________,
1.你是设计师!春天到了,学校决定用篱笆围一个面积为
100 平方米的花圃种花.有以下两种方案:
圆形花圃:造价 12 元/米;矩形花圃:造价 10 元/米;
你觉得哪个方案更省钱呢?
2.在问题 1 中,假若现在只有 36 米的篱笆可用,怎么样
设计才能使得矩形花圃的面积最大?
题型1
基本不等式在(函数)最值中的应用
【变式与拓展】
题型2
利用基本不等式进行优化设计(最大值问题)
例2:某村计划建造一个室内面积为 800 m2 的矩形蔬菜温
室.在温室内,沿左、右两侧与后侧内墙各保留 1 m 宽的通道,
沿前侧内墙保留 3 m 宽的空地.当矩形温室的边长各为多少
时?蔬菜的种植面积最大,最大种植面积是多少?
自主解答:设矩形温室的左侧边长为 a m,后侧边长为 b m,
则 ab=800.
蔬菜的种植面积
S=(a-4)(b-2)=ab-4b-2a+8=808-2(a+2b).
所以 S≤808-4 =648(m2).
当 a=2b,即 a=40(m),b=20(m)时,S最大值=648(m2).
答:当矩形温室的左侧边长为 40 m,后侧边长为 20 m 时,
蔬菜的种植面积最大,最大种植面积为 648 m2.
【变式与拓展】
2.某单位用 2 160 万元购得一块空地,计划在该地块上建
造一栋至少 10 层,每层 2 000 平方米的楼房.经测算,如果将
楼房建为 x(x≥10) 层,则每平方米的平均建筑费用为 560 +
48x(单位:元).为了使楼房每平方米的平均综合费用最少,则
)
B
楼房应建为(
A.10 层
C.20 层
B.15 层
D.30 层
题型3
利用基本不等式进行优化设计(最小值问题)
例3:为迎接北京奥运会,北京市决定在首都国际机场粘
贴一幅“福娃”宣传画,如图 3-4-1 要求画面面积为 72 m2,
左、右各留 1 米,上、下各留 0.5 米,问怎样设计画面的长和
宽才能使宣传画所用纸张面积最小?
图 3-4-1
自主解答:设宣传画的长、宽分别为 x,y 米,则 xy=72,
设纸张面积为 S,则:
S=(x+2)(y+1)=xy+x+2y+2
由 xy=72,即 y=
72
x
代入上式,
得 S=74+x+
144
x
≥74+2
=98,
当且仅当 x=
144
x
,即 x=12 时,Smin=98.
所以宣传画的长为 12 米,宽为 6 米,所用纸张面积最小.
【变式与拓展】
3.设计一幅宣传画,要求画面面积 4 840 cm2,画面的上、
下各留 8 cm 的空白,左右各留 5 cm 的空白.怎样确定画面的
高与宽的尺寸,能使宣传画所用纸张最小?
(2)修1m旧墙的费用是—元;
(3)拆去1m旧墙,用所得的材料建1m新墙的费用为—元.
例4:某工厂有旧墙 14 m,现准备利用这面旧墙建造平面
图形为矩形,面积为 126 m2 的厂房,工程条件是:
(1)建 1 m 新墙的费用为 a 元;
a
4
a
2
经讨论有两种方案:
(1)利用旧墙的一段 x m(x<14)为矩形厂房的一面的边长;
(2)矩形一面的边长 x≥14 m.
问如何利用旧墙,即 x 为多少时建墙费用最省?
易错点评:在实际问题中,没有考虑“等号”是否成立,
以至出错.此题是生活实际中常碰到的,有实际意义,综合分
析能力很强,尤其(2)x≥14,往往容易疏忽,不加以考虑,仅以
(1)分析,利用部分旧墙,拆除部分旧墙,用拆得的材料建新墙,
其余的建新墙,虽然结果正确,但没有与(2)作比较,不能算是
一种完整的解法.
1.不等式的应用问题大都与函数相关联,在求最值时,基
本不等式是经常使用的工具,但若对自变量有限制,一定要注
意等号能否取得,若取不到,则必须利用函数的单调性去求函
数的最值.
2.解答不等式应用题的一般步骤:
(1)阅读并理解材料;
(2)建立数学模型;
(3)讨论不等关系;
(4)作出结论.
