人教版六下 面积与周长的再认识 复习教案
文档属性
| 名称 | 人教版六下 面积与周长的再认识 复习教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 1005.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 00:00:00 | ||
图片预览




文档简介
面积与周长的再认识
—— 平面图形测量的整理与复习
学生情况分析:
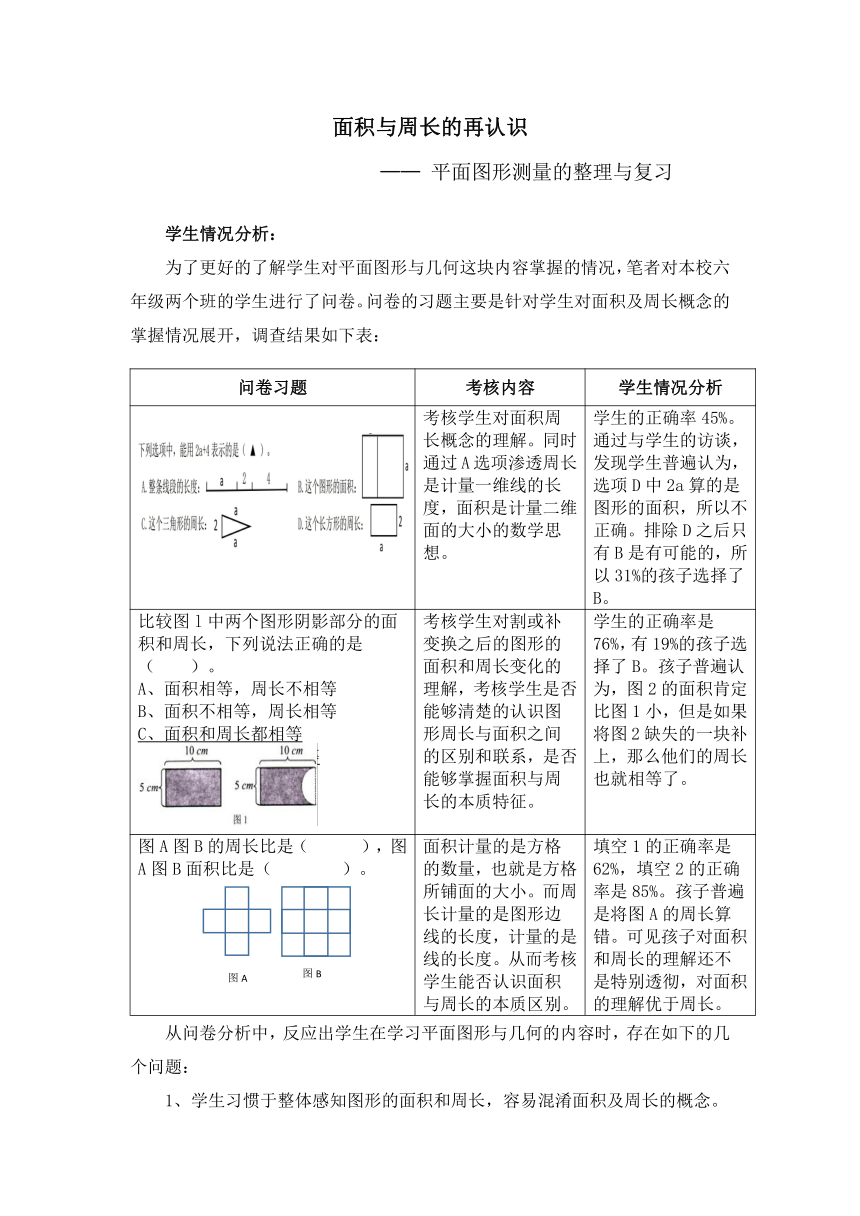
为了更好的了解学生对平面图形与几何这块内容掌握的情况,笔者对本校六年级两个班的学生进行了问卷。问卷的习题主要是针对学生对面积及周长概念的掌握情况展开,调查结果如下表:
问卷习题 考核内容 学生情况分析
考核学生对面积周长概念的理解。同时通过A选项渗透周长是计量一维线的长度,面积是计量二维面的大小的数学思想。 学生的正确率45%。通过与学生的访谈,发现学生普遍认为,选项D中2a算的是图形的面积,所以不正确。排除D之后只有B是有可能的,所以31%的孩子选择了B。
比较图l中两个图形阴影部分的面积和周长,下列说法正确的是( )。
A、面积相等,周长不相等
B、面积不相等,周长相等
C、面积和周长都相等
D、面积和周长都不相等 考核学生对割或补变换之后的图形的面积和周长变化的理解,考核学生是否能够清楚的认识图形周长与面积之间的区别和联系,是否能够掌握面积与周长的本质特征。 学生的正确率是76%,有19%的孩子选择了B。孩子普遍认为,图2的面积肯定比图1小,但是如果将图2缺失的一块补上,那么他们的周长也就相等了。
图A图B的周长比是( ),图A图B面积比是( )。 面积计量的是方格的数量,也就是方格所铺面的大小。而周长计量的是图形边线的长度,计量的是线的长度。从而考核学生能否认识面积与周长的本质区别。 填空1的正确率是62%,填空2的正确率是85%。孩子普遍是将图A的周长算错。可见孩子对面积和周长的理解还不是特别透彻,对面积的理解优于周长。
从问卷分析中,反应出学生在学习平面图形与几何的内容时,存在如下的几个问题:
学生习惯于整体感知图形的面积和周长,容易混淆面积及周长的概念。
面积指向对图形整体的认知,而周长指向的是对图形局部的认识,所以学生对面积的认识会优于对周长的认识。
学生比较习惯于计算规则图形的周长,而对求非规则图形的周长,孩子存在一定的困难,这也体现出学生没有真正理解周长的概念。
目 标:
通过以上对学生的分析,及学生在学习平面图形的面积及周长存在的问题,笔者希望通过这样一系列习题串的设计,能够达到如下的目标:
在经历探究周长是计量一维的线的长度,面积是计量二维面的大小的过程中,厘清周长和面积概念,理解周长和面积概念的本质。
在感悟面积不变周长变,周长不变面积变的过程中,进一步理解面积周长的概念,同时渗透变与不变的数学思想。
在经历探究面积的变化与图形底和高之间关系的过程中,对平面图形的面积形成整体认知,进一步发展学生的空间观念。
经历探索直边图形与曲边图形面积周长之间的关系,感受直边图形与曲边图形的密切联系,发展学生的空间思维能力。
经历画阴影部分面积相等图形的过程,并探讨图形之间面积及周长的关系,发展学生的空间思维及创新能力。
习题设计:
〖主题再现〗
〖主题来源〗人教版教材三年级下册69页练习十五第10题。
〖主题解读〗该习题是安排在练习十五的最后一题,是学生会计算长方形正方形的面积之后的一道巩固练习。这一题是一道开放题,教材试图通过这一题,一方面引导学生发现在一个长方形的边上剪掉一个长方形,会有三种主要的不同情况:其一是在中间剪,这是一种常见的方法,学生大多能够想到;其二是在角落上剪,这个部分学生也没有问题;其三是中间竖着剪,这种往往学生较难想到。从而在多种策略的讨论中,发展孩子的空间思维。另一方面,让学生在讨论中经历面积不变,周长变的过程,引导学生在体会变与不变的过程中进一步厘清周长和面积的概念,从而理解面积及周长概念的本质。
学生可能出现的情况:学生对于面积不变比较容易理解,但是对于周长的变化,在理解上存在一定困难,教师在教学中需要为学生设计边动态平移的过程,帮助学生更直观的去理解周长的变化。另外,受思维定式影响,学生大多都会认为就是在长方形中间剪掉一个长方形,而且认为周长没有变化。对于其它两种情况,孩子较难想到,特别是最后一种方法,需要在老师的启发之下才能发现。
〖教学提示〗为了更好的发挥本题厘清面积及周长概念的作用,发展学生空间思维。我决定对此题做如下处理:
先呈现习题(文字),在学生汇报之后,再呈现图形,引导学生在比较中归纳主要的三种情况,及周长的变化规律。
借助格子图,让学生通过格子图感受面积都是相同的,而周长一直在变化:沿着四个角落剪周长不变,沿着中间减,一种情况是增加两条宽,另一种情况是增加两条长。
利用课件,动画呈现第一个图形的周长,将周长拼接成一条线,让学生直观感受,周长就是计量一维线的长度。面积是计量二维的面的大小,也就是数铺满这个图形的格子有多少个。从而达到真正理解周长面积概念的本质。
课件动态演示将长方形的周展开形成一条线的过程:
关联题一
〖题目呈现〗
〖题目来源〗人教版教材五年级上册第90页练习十九多边形的面积第8题。
〖选择理由〗此题安排在学生学行四边形的面积之后进行练习,让学生在拉动长方形的过程中,感受四条小棒的长度一直没有发生变化,也就是四边形的周长始终不变,但是随着平行四边形高的不断变短面积会越来越小。从而进一步巩固,平行四边形的面积与底和高的关系。让学生在经历这种动态的变化过程中,进一步理解周长和面积的本质特征。
与主习题的关系:主习题是面积不变周长变,该习题是周长不变面积在变,两个习题都是试图在这种变与不变中,帮助学生认识面积与周长的联系与区别,帮助学生厘清面积与周长的概念。同时感受图形的面积相等周长不一定相等,周长相等面积不一定相等,发展学生的空间思维能力。
而该习题与主习题不一样的是,主习题是一种静态的呈现面积与周长的变化,该习题是动态的呈现面积与周长的变化,更有利于学生厘清面积与周长的概念,更有利于发展学生的空间观念。另外,长方形在变化的过程中,底始终保持不变,而高一直在变化,从而使学生进一步意识到,平行四边形的底和高这两个维度决定了平行四边形的面积。
〖教学提示〗
1、学生自主思考:周长和面积是怎样变化的?
2、追问:为什么周长不变面积变小。引导得出:不管图形怎么变都是由四根木条围成,所以周长不变,而图形的大小越变越小(面积变小)。
3、思考:图形的面积变小和什么有关系?引导得出:平行四边形的底和高,决定面积的大小。
关联习题二
〖题目呈现〗
〖题目来源〗人教版教材六年级下册第89页练习十八图形与几何复习板块第5题。
〖选择理由〗该习题是主习题的进一步发展和延续,通过主习题学生已经理清了周长和面积概念的本质特征。此题通过画面积与平行四边形面积相等的平面的图形,使学生进一步认识决定图形面积大小的两个关键因素是图形的底和高。并通过多媒体课件的演示,进一步发现平面图形通过割补都能得到一个底(长)和高(宽)都相等的长方形。使学生理解图形的面积是由底和高两个因素决定的。底和高这两个维度,其实就是长方形的长和宽。在方格图中我们会发现,底就是横排有几个方格,高也就是纵排有几个方格。他们的乘积也就是图形所占方格的数量也就是图形的面积。所以底和高这两个维度决定着图形的面积,从而构建对小学阶段平面图形面积的整体认知。
〖教学提示〗
学生自主画与平行四边形面积相等的图形,如三角形,长方形,梯形等。
展示学生作品(底相等的情况)提问:这些图形有什么相同的地方和不同的地方?为什么?引导得到:底都相等,三角形的高和梯形的高是平行四边形的两倍。
通过动画演示将平行四边形、三角形、梯形、都变成完全一样的长方形。提问:你发现了什么?(引导得到:三角形和梯形的高除以2其实求得就是转化后长方形的宽)
想一想为什么这些图形的面积都是有底和高决定的?引导得到:所有图形最终都可以转化成长方形,长方形的长(图形的底)决定横排方格的数量,长方形的宽(图形的高)决定纵排方格的数量。他们的乘绩就是图形的方格数,也就是图形的面积,所以图形的长和宽决定图形面积的大小(如下图)。
关联习题三
〖题目呈现〗
〖题目来源〗苍南县2020年六年级毕业测试卷填空题第18题。
〖选择理由〗此题已知圆的半径等于长方形的宽,圆的面积等于长方形的面积,里面隐藏的信息是:长方形的长等于圆周长的一半。这个隐藏的信息,学生难以发现,往往是教师直接告知学生。
当我们回到圆的面积的推导过程,我们发现将一个圆通过割补的方法,转化成长方形,这个时候长方形的面积就是Πr乘r。此题中长方形的面积是r乘长,由于他们的面积相等,所以长方形的长也就等于Πr,也就是圆周长的一半,所以此时的长方形就等同于由圆进行割补得到的长方形。如果学生弄明白了这一点,这一题也就不攻自破了。
这和主习题又有怎样的联系呢?小学阶段平面图形的面积与周长,只有两种情况,一种是直边图形,一种是曲边图形。所以探讨周长和面积肯定离不开圆的的面积和周长。所以这一题是对主习题的补充和延伸。对于曲边图形的周长和面积我们采用的通常都是化圆为方,化曲为直的方法。在这种圆与方的转化过程中,可以进一步巩固学生对周长和面积概念的理解,同时让学生感受曲边图形与直边图形之间的联系,有助于学生对平面图形形成一个整体的认知,发展学生的空间观念。
〖教学提示〗
学生自主完成练习。
提问:除了圆的半径就是长方形的宽,那么长方形的长和圆又有什么关系呢?
想一想,我们是怎么求圆的面积的,他们之间有什么样的关联?引导得到:此时的长方形,就相当于将圆切成无数个扇形所拼成的一个最完美的长方形。从而帮助学生理解此题,同时也打通了曲边图形与直边图形之间的联系。
沟通两种情况下圆与方的关系,及两种情况之间的联系:
关联习题四
〖题目呈现〗
〖题目来源〗六年级下册课堂作业本63页第6题,图形与几何的复习内容。
〖选择理由〗让学生在割与补中感受周长和面积的变化,此题是主习题的延申和拓展,也是主习题的补充。在前面学生通过静态和动态、化曲为直、化直为方等多个角度认识了周长和面积的本质特征,此题是通过割和补来认识周长和面积的变化,是对前面的巩固和提升。
对于图形的面积通过割补不改变大小的特性,学生掌握的较好。但是对于周长是怎样变化,部分学生在认知上还是有些模糊。所以通过本题的探索和学习,帮助学生更好的理解图形割补以后周长的变化情况,引导学生归纳什么情况周长会增加生么情况周长会减少,打破学生关于周长认识的最后一块壁垒。促进学生空间思维的发展。
〖教学提示〗
1、学生自主完成习题。
2、展示学生作品提问:将图形进行割补以后,图形的什么变了?什么不变?
3、关于图形的周长是如何计算的?也是用割补的方法吗?(引导得出:周长求的是一维线的长度,不能割补,只能应用拼接的方法。)
关联习题五
〖题目呈现〗
〖题目来源〗根据书中练习改编,适合六年级学生。
〖选择理由〗该题是在学生完成前面几题的基础上展开学习,通过前面习题的学习,对于面积及周长本质特征学生已经有了很好的理解。法国著名的数学家说:我们是通过逻辑去证明,但是我们是通过直观去创造。可见空间与图形内容的学习,对发展孩子的创新能力至关重要。所以为了更好的发展孩子的创新思维,笔者在原来习题的基础上曾加了第二个问题,再通过引导学生根据图形周长的特点对图形进行分类,巩固孩子对周长和面积概念的理解。
〖教学提示〗
1、学生自主完成练习(1)(2)小题。
2、呈现学生作品,请根据这些图形的周长的特点,对这些图形(如下图)进行分类。
〖畅谈收获〗同学们通过这节课的学习,你有什么收获?
反思与困惑:
本节课的目标是想通过串联这五道练习,完成对整个小学阶段平面图形面积与周长这块内容的复习和梳理,同时渗透化圆为方、转化、割补的数学思想方法。能不能达到效果,还需要后期孩子在学习中进一步去验证。但是这种以一个系列的习题,来串起一个版块内容的复习方式,是非常有益的,避免了题海战术,提高了课堂的效率,也使学生的能力有所发展。
通过这五个练习的学习,学生对面积和周长的概念,有了更加清晰的认识,对平面图形形成了一个更加整体的认知,学生的空间思维也得到了一定的发展。但一些中下的学生,在完成习题时,明显感觉困难,需要在老师和同伴的帮助下完成。那么如何更加全面的去了解学生的学情,发展孩子的空间思维,使他们也能够主动的参与到课堂中来,这是今后教学中需要去改进的地方。
在实践的过程中,也遇到了这样的两个问题:
习题串里面习题的类型是有限的,当学生在解决问题中遇到不同类型的问题时他是否能够自主解决 学生自主解题能力应当如何养成?
2、这样的习题教学,是否也要像我们的常态课堂一样,让学生经历完整的探究过程?如果需要我们的课堂时间又该如何去把控?
—— 平面图形测量的整理与复习
学生情况分析:
为了更好的了解学生对平面图形与几何这块内容掌握的情况,笔者对本校六年级两个班的学生进行了问卷。问卷的习题主要是针对学生对面积及周长概念的掌握情况展开,调查结果如下表:
问卷习题 考核内容 学生情况分析
考核学生对面积周长概念的理解。同时通过A选项渗透周长是计量一维线的长度,面积是计量二维面的大小的数学思想。 学生的正确率45%。通过与学生的访谈,发现学生普遍认为,选项D中2a算的是图形的面积,所以不正确。排除D之后只有B是有可能的,所以31%的孩子选择了B。
比较图l中两个图形阴影部分的面积和周长,下列说法正确的是( )。
A、面积相等,周长不相等
B、面积不相等,周长相等
C、面积和周长都相等
D、面积和周长都不相等 考核学生对割或补变换之后的图形的面积和周长变化的理解,考核学生是否能够清楚的认识图形周长与面积之间的区别和联系,是否能够掌握面积与周长的本质特征。 学生的正确率是76%,有19%的孩子选择了B。孩子普遍认为,图2的面积肯定比图1小,但是如果将图2缺失的一块补上,那么他们的周长也就相等了。
图A图B的周长比是( ),图A图B面积比是( )。 面积计量的是方格的数量,也就是方格所铺面的大小。而周长计量的是图形边线的长度,计量的是线的长度。从而考核学生能否认识面积与周长的本质区别。 填空1的正确率是62%,填空2的正确率是85%。孩子普遍是将图A的周长算错。可见孩子对面积和周长的理解还不是特别透彻,对面积的理解优于周长。
从问卷分析中,反应出学生在学习平面图形与几何的内容时,存在如下的几个问题:
学生习惯于整体感知图形的面积和周长,容易混淆面积及周长的概念。
面积指向对图形整体的认知,而周长指向的是对图形局部的认识,所以学生对面积的认识会优于对周长的认识。
学生比较习惯于计算规则图形的周长,而对求非规则图形的周长,孩子存在一定的困难,这也体现出学生没有真正理解周长的概念。
目 标:
通过以上对学生的分析,及学生在学习平面图形的面积及周长存在的问题,笔者希望通过这样一系列习题串的设计,能够达到如下的目标:
在经历探究周长是计量一维的线的长度,面积是计量二维面的大小的过程中,厘清周长和面积概念,理解周长和面积概念的本质。
在感悟面积不变周长变,周长不变面积变的过程中,进一步理解面积周长的概念,同时渗透变与不变的数学思想。
在经历探究面积的变化与图形底和高之间关系的过程中,对平面图形的面积形成整体认知,进一步发展学生的空间观念。
经历探索直边图形与曲边图形面积周长之间的关系,感受直边图形与曲边图形的密切联系,发展学生的空间思维能力。
经历画阴影部分面积相等图形的过程,并探讨图形之间面积及周长的关系,发展学生的空间思维及创新能力。
习题设计:
〖主题再现〗
〖主题来源〗人教版教材三年级下册69页练习十五第10题。
〖主题解读〗该习题是安排在练习十五的最后一题,是学生会计算长方形正方形的面积之后的一道巩固练习。这一题是一道开放题,教材试图通过这一题,一方面引导学生发现在一个长方形的边上剪掉一个长方形,会有三种主要的不同情况:其一是在中间剪,这是一种常见的方法,学生大多能够想到;其二是在角落上剪,这个部分学生也没有问题;其三是中间竖着剪,这种往往学生较难想到。从而在多种策略的讨论中,发展孩子的空间思维。另一方面,让学生在讨论中经历面积不变,周长变的过程,引导学生在体会变与不变的过程中进一步厘清周长和面积的概念,从而理解面积及周长概念的本质。
学生可能出现的情况:学生对于面积不变比较容易理解,但是对于周长的变化,在理解上存在一定困难,教师在教学中需要为学生设计边动态平移的过程,帮助学生更直观的去理解周长的变化。另外,受思维定式影响,学生大多都会认为就是在长方形中间剪掉一个长方形,而且认为周长没有变化。对于其它两种情况,孩子较难想到,特别是最后一种方法,需要在老师的启发之下才能发现。
〖教学提示〗为了更好的发挥本题厘清面积及周长概念的作用,发展学生空间思维。我决定对此题做如下处理:
先呈现习题(文字),在学生汇报之后,再呈现图形,引导学生在比较中归纳主要的三种情况,及周长的变化规律。
借助格子图,让学生通过格子图感受面积都是相同的,而周长一直在变化:沿着四个角落剪周长不变,沿着中间减,一种情况是增加两条宽,另一种情况是增加两条长。
利用课件,动画呈现第一个图形的周长,将周长拼接成一条线,让学生直观感受,周长就是计量一维线的长度。面积是计量二维的面的大小,也就是数铺满这个图形的格子有多少个。从而达到真正理解周长面积概念的本质。
课件动态演示将长方形的周展开形成一条线的过程:
关联题一
〖题目呈现〗
〖题目来源〗人教版教材五年级上册第90页练习十九多边形的面积第8题。
〖选择理由〗此题安排在学生学行四边形的面积之后进行练习,让学生在拉动长方形的过程中,感受四条小棒的长度一直没有发生变化,也就是四边形的周长始终不变,但是随着平行四边形高的不断变短面积会越来越小。从而进一步巩固,平行四边形的面积与底和高的关系。让学生在经历这种动态的变化过程中,进一步理解周长和面积的本质特征。
与主习题的关系:主习题是面积不变周长变,该习题是周长不变面积在变,两个习题都是试图在这种变与不变中,帮助学生认识面积与周长的联系与区别,帮助学生厘清面积与周长的概念。同时感受图形的面积相等周长不一定相等,周长相等面积不一定相等,发展学生的空间思维能力。
而该习题与主习题不一样的是,主习题是一种静态的呈现面积与周长的变化,该习题是动态的呈现面积与周长的变化,更有利于学生厘清面积与周长的概念,更有利于发展学生的空间观念。另外,长方形在变化的过程中,底始终保持不变,而高一直在变化,从而使学生进一步意识到,平行四边形的底和高这两个维度决定了平行四边形的面积。
〖教学提示〗
1、学生自主思考:周长和面积是怎样变化的?
2、追问:为什么周长不变面积变小。引导得出:不管图形怎么变都是由四根木条围成,所以周长不变,而图形的大小越变越小(面积变小)。
3、思考:图形的面积变小和什么有关系?引导得出:平行四边形的底和高,决定面积的大小。
关联习题二
〖题目呈现〗
〖题目来源〗人教版教材六年级下册第89页练习十八图形与几何复习板块第5题。
〖选择理由〗该习题是主习题的进一步发展和延续,通过主习题学生已经理清了周长和面积概念的本质特征。此题通过画面积与平行四边形面积相等的平面的图形,使学生进一步认识决定图形面积大小的两个关键因素是图形的底和高。并通过多媒体课件的演示,进一步发现平面图形通过割补都能得到一个底(长)和高(宽)都相等的长方形。使学生理解图形的面积是由底和高两个因素决定的。底和高这两个维度,其实就是长方形的长和宽。在方格图中我们会发现,底就是横排有几个方格,高也就是纵排有几个方格。他们的乘积也就是图形所占方格的数量也就是图形的面积。所以底和高这两个维度决定着图形的面积,从而构建对小学阶段平面图形面积的整体认知。
〖教学提示〗
学生自主画与平行四边形面积相等的图形,如三角形,长方形,梯形等。
展示学生作品(底相等的情况)提问:这些图形有什么相同的地方和不同的地方?为什么?引导得到:底都相等,三角形的高和梯形的高是平行四边形的两倍。
通过动画演示将平行四边形、三角形、梯形、都变成完全一样的长方形。提问:你发现了什么?(引导得到:三角形和梯形的高除以2其实求得就是转化后长方形的宽)
想一想为什么这些图形的面积都是有底和高决定的?引导得到:所有图形最终都可以转化成长方形,长方形的长(图形的底)决定横排方格的数量,长方形的宽(图形的高)决定纵排方格的数量。他们的乘绩就是图形的方格数,也就是图形的面积,所以图形的长和宽决定图形面积的大小(如下图)。
关联习题三
〖题目呈现〗
〖题目来源〗苍南县2020年六年级毕业测试卷填空题第18题。
〖选择理由〗此题已知圆的半径等于长方形的宽,圆的面积等于长方形的面积,里面隐藏的信息是:长方形的长等于圆周长的一半。这个隐藏的信息,学生难以发现,往往是教师直接告知学生。
当我们回到圆的面积的推导过程,我们发现将一个圆通过割补的方法,转化成长方形,这个时候长方形的面积就是Πr乘r。此题中长方形的面积是r乘长,由于他们的面积相等,所以长方形的长也就等于Πr,也就是圆周长的一半,所以此时的长方形就等同于由圆进行割补得到的长方形。如果学生弄明白了这一点,这一题也就不攻自破了。
这和主习题又有怎样的联系呢?小学阶段平面图形的面积与周长,只有两种情况,一种是直边图形,一种是曲边图形。所以探讨周长和面积肯定离不开圆的的面积和周长。所以这一题是对主习题的补充和延伸。对于曲边图形的周长和面积我们采用的通常都是化圆为方,化曲为直的方法。在这种圆与方的转化过程中,可以进一步巩固学生对周长和面积概念的理解,同时让学生感受曲边图形与直边图形之间的联系,有助于学生对平面图形形成一个整体的认知,发展学生的空间观念。
〖教学提示〗
学生自主完成练习。
提问:除了圆的半径就是长方形的宽,那么长方形的长和圆又有什么关系呢?
想一想,我们是怎么求圆的面积的,他们之间有什么样的关联?引导得到:此时的长方形,就相当于将圆切成无数个扇形所拼成的一个最完美的长方形。从而帮助学生理解此题,同时也打通了曲边图形与直边图形之间的联系。
沟通两种情况下圆与方的关系,及两种情况之间的联系:
关联习题四
〖题目呈现〗
〖题目来源〗六年级下册课堂作业本63页第6题,图形与几何的复习内容。
〖选择理由〗让学生在割与补中感受周长和面积的变化,此题是主习题的延申和拓展,也是主习题的补充。在前面学生通过静态和动态、化曲为直、化直为方等多个角度认识了周长和面积的本质特征,此题是通过割和补来认识周长和面积的变化,是对前面的巩固和提升。
对于图形的面积通过割补不改变大小的特性,学生掌握的较好。但是对于周长是怎样变化,部分学生在认知上还是有些模糊。所以通过本题的探索和学习,帮助学生更好的理解图形割补以后周长的变化情况,引导学生归纳什么情况周长会增加生么情况周长会减少,打破学生关于周长认识的最后一块壁垒。促进学生空间思维的发展。
〖教学提示〗
1、学生自主完成习题。
2、展示学生作品提问:将图形进行割补以后,图形的什么变了?什么不变?
3、关于图形的周长是如何计算的?也是用割补的方法吗?(引导得出:周长求的是一维线的长度,不能割补,只能应用拼接的方法。)
关联习题五
〖题目呈现〗
〖题目来源〗根据书中练习改编,适合六年级学生。
〖选择理由〗该题是在学生完成前面几题的基础上展开学习,通过前面习题的学习,对于面积及周长本质特征学生已经有了很好的理解。法国著名的数学家说:我们是通过逻辑去证明,但是我们是通过直观去创造。可见空间与图形内容的学习,对发展孩子的创新能力至关重要。所以为了更好的发展孩子的创新思维,笔者在原来习题的基础上曾加了第二个问题,再通过引导学生根据图形周长的特点对图形进行分类,巩固孩子对周长和面积概念的理解。
〖教学提示〗
1、学生自主完成练习(1)(2)小题。
2、呈现学生作品,请根据这些图形的周长的特点,对这些图形(如下图)进行分类。
〖畅谈收获〗同学们通过这节课的学习,你有什么收获?
反思与困惑:
本节课的目标是想通过串联这五道练习,完成对整个小学阶段平面图形面积与周长这块内容的复习和梳理,同时渗透化圆为方、转化、割补的数学思想方法。能不能达到效果,还需要后期孩子在学习中进一步去验证。但是这种以一个系列的习题,来串起一个版块内容的复习方式,是非常有益的,避免了题海战术,提高了课堂的效率,也使学生的能力有所发展。
通过这五个练习的学习,学生对面积和周长的概念,有了更加清晰的认识,对平面图形形成了一个更加整体的认知,学生的空间思维也得到了一定的发展。但一些中下的学生,在完成习题时,明显感觉困难,需要在老师和同伴的帮助下完成。那么如何更加全面的去了解学生的学情,发展孩子的空间思维,使他们也能够主动的参与到课堂中来,这是今后教学中需要去改进的地方。
在实践的过程中,也遇到了这样的两个问题:
习题串里面习题的类型是有限的,当学生在解决问题中遇到不同类型的问题时他是否能够自主解决 学生自主解题能力应当如何养成?
2、这样的习题教学,是否也要像我们的常态课堂一样,让学生经历完整的探究过程?如果需要我们的课堂时间又该如何去把控?
