2021-2022学年鲁教版(五四制)九年级数学下册5.10圆锥的侧面积 选择题专题训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)九年级数学下册5.10圆锥的侧面积 选择题专题训练(Word版含答案) | 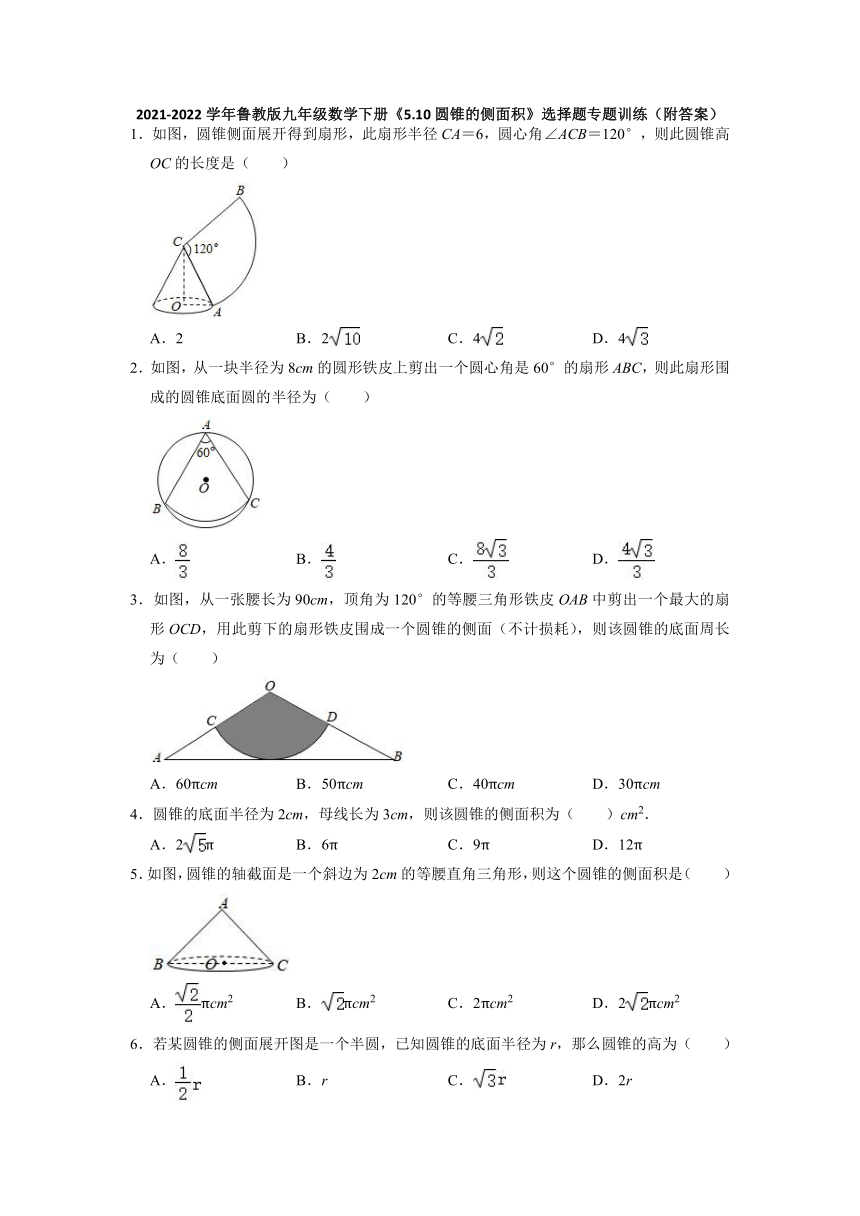 | |
| 格式 | doc | ||
| 文件大小 | 247.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 09:55:57 | ||
图片预览



文档简介
2021-2022学年鲁教版九年级数学下册《5.10圆锥的侧面积》选择题专题训练(附答案)
1.如图,圆锥侧面展开得到扇形,此扇形半径CA=6,圆心角∠ACB=120°,则此圆锥高OC的长度是( )
A.2 B.2 C.4 D.4
2.如图,从一块半径为8cm的圆形铁皮上剪出一个圆心角是60°的扇形ABC,则此扇形围成的圆锥底面圆的半径为( )
A. B. C. D.
3.如图,从一张腰长为90cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面周长为( )
A.60πcm B.50πcm C.40πcm D.30πcm
4.圆锥的底面半径为2cm,母线长为3cm,则该圆锥的侧面积为( )cm2.
A.2π B.6π C.9π D.12π
5.如图,圆锥的轴截面是一个斜边为2cm的等腰直角三角形,则这个圆锥的侧面积是( )
A.πcm2 B.πcm2 C.2πcm2 D.2πcm2
6.若某圆锥的侧面展开图是一个半圆,已知圆锥的底面半径为r,那么圆锥的高为( )
A. B.r C. D.2r
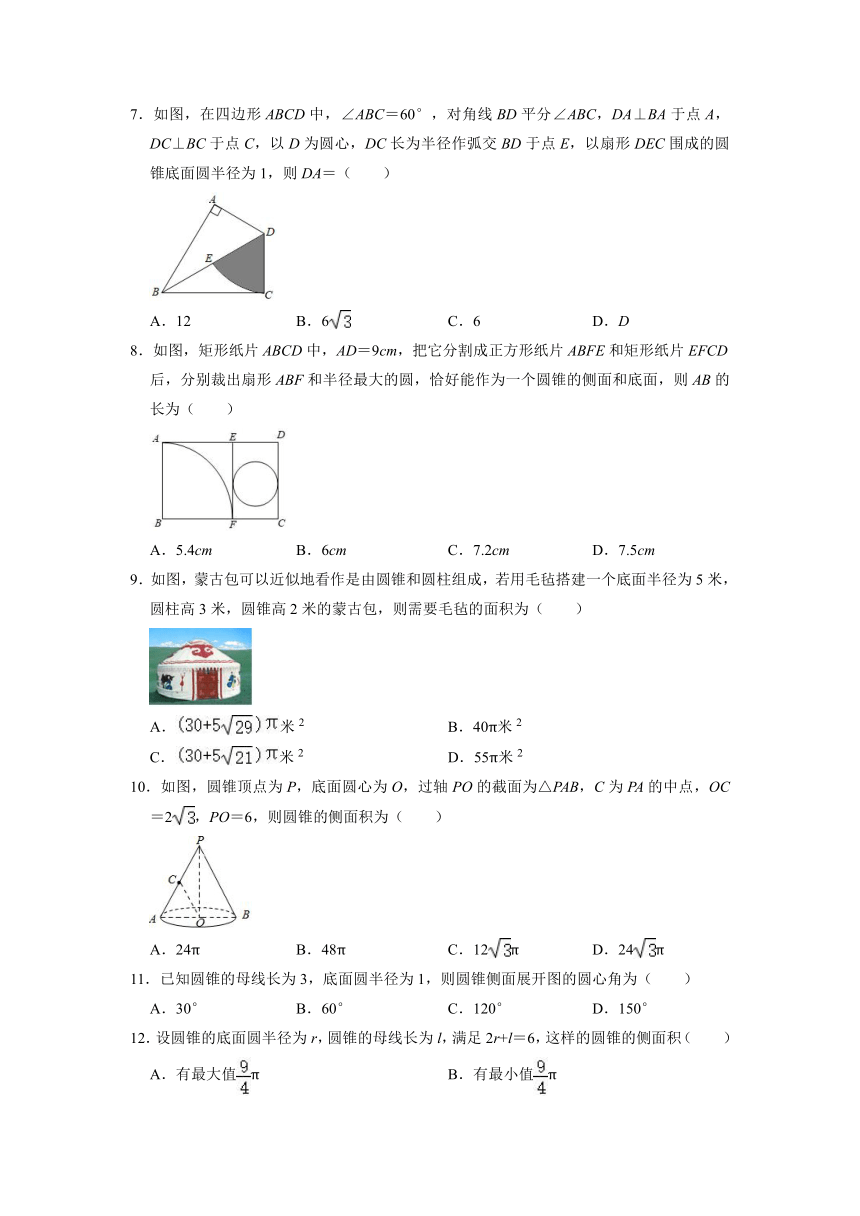
7.如图,在四边形ABCD中,∠ABC=60°,对角线BD平分∠ABC,DA⊥BA于点A,DC⊥BC于点C,以D为圆心,DC长为半径作弧交BD于点E,以扇形DEC围成的圆锥底面圆半径为1,则DA=( )
A.12 B.6 C.6 D.D
8.如图,矩形纸片ABCD中,AD=9cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB的长为( )
A.5.4cm B.6cm C.7.2cm D.7.5cm
9.如图,蒙古包可以近似地看作是由圆锥和圆柱组成,若用毛毡搭建一个底面半径为5米,圆柱高3米,圆锥高2米的蒙古包,则需要毛毡的面积为( )
A.米2 B.40π米2
C.米2 D.55π米2
10.如图,圆锥顶点为P,底面圆心为O,过轴PO的截面为△PAB,C为PA的中点,OC=2,PO=6,则圆锥的侧面积为( )
A.24π B.48π C.12π D.24π
11.已知圆锥的母线长为3,底面圆半径为1,则圆锥侧面展开图的圆心角为( )
A.30° B.60° C.120° D.150°
12.设圆锥的底面圆半径为r,圆锥的母线长为l,满足2r+l=6,这样的圆锥的侧面积( )
A.有最大值π B.有最小值π
C.有最大值π D.有最小值π
13.用半径为30cm,圆心角为120°的扇形纸片恰好能围成一个圆锥的侧面,则这个圆锥底面半径为( )
A.5cm B.10cm C.15cm D.20cm
14.将一个圆锥展开后,其侧面是一个圆心角为108°,半径为12cm的扇形,则该圆锥的底面半径是( )
A.1.8cm B.3.6cm C.4cm D.6cm
15.如图,在Rt△ABC 中,∠C=90°,AC=1,BC=,若把△ABC绕边AB所在的直线旋转一周,则所得几何体的表面积为( )
A.(+3)π B.π C.2π D.(2+3)π
16.如图,已知扇形OAB的半径为6cm,圆心角的度数为120°,若将OA,OB重合后围成一圆锥侧面,那么圆锥的底面半径为( )
A.2cm B.3cm C.6cm D.2cm
17.如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4.把△ABC分别绕直线AB,BC和AC旋转一周,所得几何体的表面积分别记作S1,S2,S3,则表面积最大的是( )
A.S1 B.S2 C.S3 D.无法确定
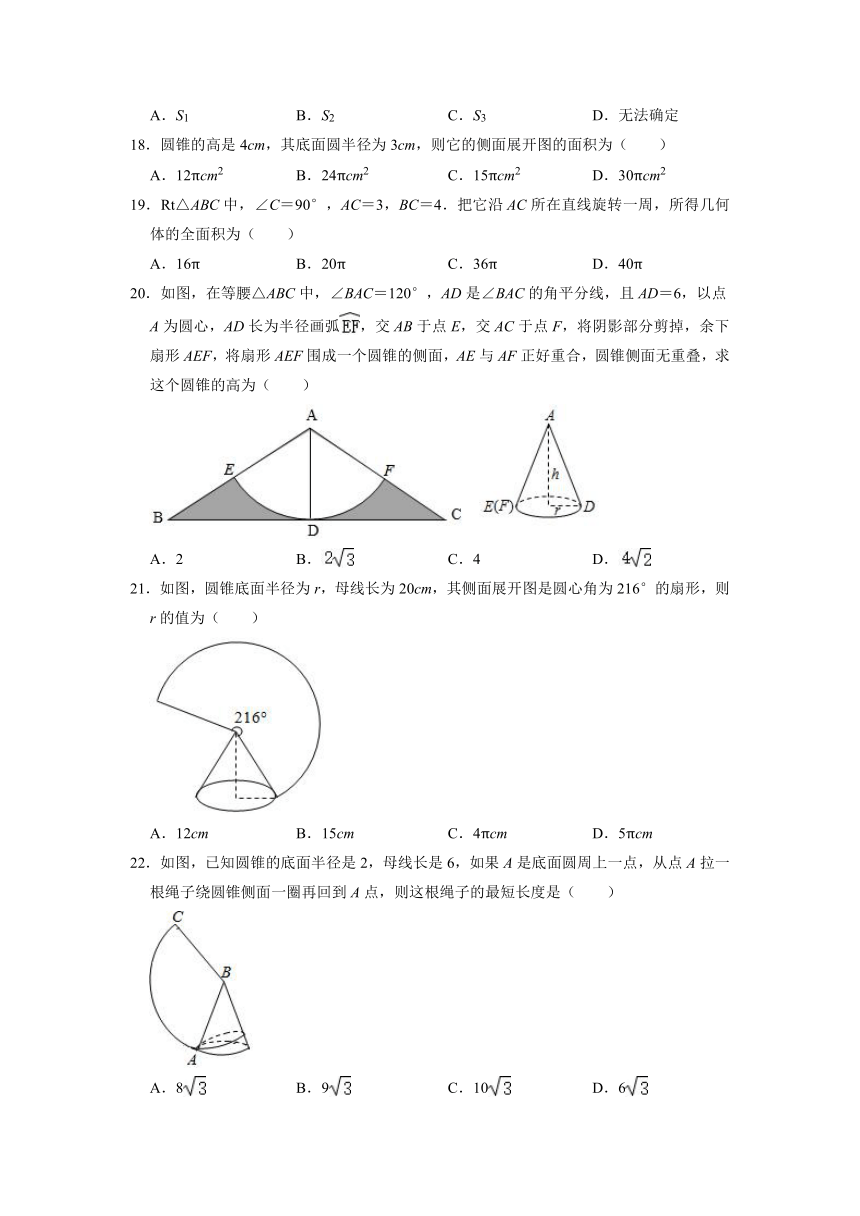
18.圆锥的高是4cm,其底面圆半径为3cm,则它的侧面展开图的面积为( )
A.12πcm2 B.24πcm2 C.15πcm2 D.30πcm2
19.Rt△ABC中,∠C=90°,AC=3,BC=4.把它沿AC所在直线旋转一周,所得几何体的全面积为( )
A.16π B.20π C.36π D.40π
20.如图,在等腰△ABC中,∠BAC=120°,AD是∠BAC的角平分线,且AD=6,以点A为圆心,AD长为半径画弧,交AB于点E,交AC于点F,将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高为( )
A.2 B. C.4 D.
21.如图,圆锥底面半径为r,母线长为20cm,其侧面展开图是圆心角为216°的扇形,则r的值为( )
A.12cm B.15cm C.4πcm D.5πcm
22.如图,已知圆锥的底面半径是2,母线长是6,如果A是底面圆周上一点,从点A拉一根绳子绕圆锥侧面一圈再回到A点,则这根绳子的最短长度是( )
A.8 B.9 C.10 D.6
23.一个底面直径是27厘米,高9厘米的圆锥体木块,分成形状大小完全相同的两个木块后,表面积比原来增加( )
A.81平方厘米 B.243平方匣米
C.121.5平方厘米 D.125.6平方厘米
24.一个圆柱和一个圆锥的底面直径相等,圆锥的高是圆柱的高的2倍,圆锥的体积是8立方分米,圆柱的体积是( )
A.36立方分米 B.12立方分米 C.8立方分米 D.4立方分米
25.一个圆柱的侧面展开正好是一个正方形,这个圆柱的底面直径与高的比是( )
A.1:π B.π:1 C.1:2π D.2π:1
26.若圆锥的底面半径为2cm,侧面展开图的面积为6πcm2,则圆锥的母线长为( )
A.1cm B.2cm C.3cm D.cm
参考答案
1.解:设圆锥底面圆的半径为r,
∵AC=6,∠ACB=120°,
∴==2πr,
∴r=2,即:OA=2,
在Rt△AOC中,OA=2,AC=6,根据勾股定理得,OC==4,
故选:C.
2.解:作OD⊥AB于D,如图,则AD=BD,
∵∠OAD=∠BAC=30°,
∴OD=OA=4cm,AD=OD=4cm,
∴AB=2AD=8cm,
设围成的底面圆的半径为rcm,
则:2πr=,
解得:r=,
故选:D.
3.解:过O作OE⊥AB于E,
∵OA=OB=90cm,∠AOB=120°,
∴∠A=∠B=30°,
∴OE=OA=45cm,
∴弧CD的长==30πcm,
∴圆锥的底面周长为30πcm,
故选:D.
4.解:底面半径是2cm,则底面周长=4πcm,圆锥的侧面积=×4π×3=6πcm2.
故选:B.
5.解:∵圆锥的轴截面是一个斜边为2cm的等腰直角三角形,
∴底面半径=1cm,母线长为cm,底面周长=2πcm,
∴圆锥的侧面积=×2π×=πcm2,
故选:B.
6.解:设扇形的半径为R,
根据题意得:=2πr,
解得:R=2r,
∴圆锥的该为=,
故选:C.
7.解:∵BD平分∠ABC,DA⊥BA,DC⊥BC,
∴∠DBC=∠ABC=30°,DA=DC,
∴∠BDC=60°,
∵以扇形DEC围成的圆锥底面圆半径为1,
∴=2π×1,解得DC=6,
∴DA=6.
故选:C.
8.解:设圆锥的底面的半径为rcm,则DE=2rcm,AE=AB=(9﹣2r)cm,
根据题意得=2πr,
解得r=,
所以AB=9﹣2r=9﹣2×=6(cm).
故选:B.
9.解:设底面圆的半径为R米,
则πR2=25π,解得R=5,
圆锥的母线长==米,
所以圆锥的侧面积= 2π 5 =5π米;
圆柱的侧面积=2π 5 3=30π米2,
所以需要毛毡的面积=(30π+5π)米2.
故选:A.
10.解:∵C为PA的中点,OC=2,
∴AP=2OC=4,
∵PO=6,
∴AO===2,
∴圆锥的侧面积为πrl=π×2×4=24π,
故选:A.
11.解:圆锥侧面展开图的弧长是:2π×1=2π,
设圆心角的度数是n度,
则=2π,
解得:n=120.
故选:C.
12.解:∵2r+l=6,
∴l=6﹣2r,
∴圆锥的侧面积S侧=πrl=πr(6﹣2r)=﹣2π(r2﹣3r)=﹣2π[(r﹣)2﹣]=﹣2π(r﹣)2+π,
∴当r=时,S侧有最大值π.
故选:C.
13.解:设圆锥的底面圆半径为rcm,依题意,得
2πr=,
解得r=10.
故选:B.
14.解:∵扇形的圆心角为108°,半径为12cm,
∴扇形弧长==7.2π(cm),
∴圆锥的底面周长为7.2πcm,
∴圆锥的底面半径==3.6(cm),
故选:B.
15.解:∵Rt△ABC中,∠ACB=90°,AC=1,BC=,
∴AB==2,
设AB边上的高为h,则×2h=×1×,
解得:h=,
∴所得两个圆锥底面半径为.
∴几何体的表面积=×2π××1+×2π××=.
故选:B.
16.解:设这个圆锥的底面圆的半径是rcm,
根据题意得2π r=,
解得r=2,
即这个圆锥的底面圆的半径是2cm.
故选:A.
17.解:∵∠ABC=90°,AB=3,BC=4,
∴AC==5.
△ABC绕直线AB旋转一周,所得几何体为圆锥,底面半径为BC=4,此圆锥的表面积为底面圆面积加扇形表面积,即S1=π×42+π×4×5=36π;
△ABC绕直线BC旋转一周,所得几何体为圆锥,底面半径为AB=3,此圆锥的表面积为底面圆面积加扇形表面积,即S2=π×32+π×3×5=24π;
△ABC绕直线AC旋转一周,所得几何体为两个共底面的圆锥,底面半径为,此圆锥的表面积为两个扇形表面积之和,即S3=π××3+π××4=.
∴S1>S2>S3.
故选:A.
18.解:这个圆锥的母线长==5,
所以这个圆锥的侧面积= 2π 3 5=15π(cm2).
故选:C.
19.解:在Rt△ABC中,∠C=90°,AC=3,BC=4,
∴AB==5,
∵把Rt△ABC绕边AC所在直线旋转一周,
∴所得的几何体的全面积为:底面半径为4,母线长为5的圆锥侧面和半径为4的圆的面积之和,
故π×4×5+π×42=36π.
故选:C.
20.解:设圆锥的底面圆的半径为r,
根据题意得2πr=,解得r=2,
这个圆锥的高h==4,
故选:D.
21.解:∵圆锥底面半径为rcm,母线长为20cm,其侧面展开图是圆心角为216°的扇形,
∴2πr=π×20,
解得r=12.
故选:A.
22.解:连接AC,过B作BD⊥AC于D,
设圆锥侧面展开图的圆心角为n°,
圆锥底面圆周长为2×2π=4π,=,
则n=120,
∵BC=BA,BD⊥AC,
∴∠ABD=60°,
由AB=6,可求得BD=3,∴AD═3,
AC=2AD=6,
即这根绳子的最短长度是6,
故选:D.
23.解:根据题干分析可得,增加部分的表面积为:
27×9÷2×2,
=243÷2×2,
=243(平方厘米),
答:表面积是243平方厘米;
故选:B.
24.解:一个圆柱和一个圆锥的底面直径相等,则它们的底面积就相等,圆柱的体积=底面积×高,
圆锥的体积=×底面积×高,
圆锥的高是圆柱的2倍,所以12立方分米.
故选:B.
25.解:这个圆柱的底面直径与高的比是d:πd=1:π.
故选:A.
26.解:根据圆锥侧面积公式:S=πrl,圆锥的底面半径为2cm,侧面展开图的面积为6πcm2,
故6π=π×2×l,
解得:l=3(cm).
故选:C.
1.如图,圆锥侧面展开得到扇形,此扇形半径CA=6,圆心角∠ACB=120°,则此圆锥高OC的长度是( )
A.2 B.2 C.4 D.4
2.如图,从一块半径为8cm的圆形铁皮上剪出一个圆心角是60°的扇形ABC,则此扇形围成的圆锥底面圆的半径为( )
A. B. C. D.
3.如图,从一张腰长为90cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面周长为( )
A.60πcm B.50πcm C.40πcm D.30πcm
4.圆锥的底面半径为2cm,母线长为3cm,则该圆锥的侧面积为( )cm2.
A.2π B.6π C.9π D.12π
5.如图,圆锥的轴截面是一个斜边为2cm的等腰直角三角形,则这个圆锥的侧面积是( )
A.πcm2 B.πcm2 C.2πcm2 D.2πcm2
6.若某圆锥的侧面展开图是一个半圆,已知圆锥的底面半径为r,那么圆锥的高为( )
A. B.r C. D.2r
7.如图,在四边形ABCD中,∠ABC=60°,对角线BD平分∠ABC,DA⊥BA于点A,DC⊥BC于点C,以D为圆心,DC长为半径作弧交BD于点E,以扇形DEC围成的圆锥底面圆半径为1,则DA=( )
A.12 B.6 C.6 D.D
8.如图,矩形纸片ABCD中,AD=9cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB的长为( )
A.5.4cm B.6cm C.7.2cm D.7.5cm
9.如图,蒙古包可以近似地看作是由圆锥和圆柱组成,若用毛毡搭建一个底面半径为5米,圆柱高3米,圆锥高2米的蒙古包,则需要毛毡的面积为( )
A.米2 B.40π米2
C.米2 D.55π米2
10.如图,圆锥顶点为P,底面圆心为O,过轴PO的截面为△PAB,C为PA的中点,OC=2,PO=6,则圆锥的侧面积为( )
A.24π B.48π C.12π D.24π
11.已知圆锥的母线长为3,底面圆半径为1,则圆锥侧面展开图的圆心角为( )
A.30° B.60° C.120° D.150°
12.设圆锥的底面圆半径为r,圆锥的母线长为l,满足2r+l=6,这样的圆锥的侧面积( )
A.有最大值π B.有最小值π
C.有最大值π D.有最小值π
13.用半径为30cm,圆心角为120°的扇形纸片恰好能围成一个圆锥的侧面,则这个圆锥底面半径为( )
A.5cm B.10cm C.15cm D.20cm
14.将一个圆锥展开后,其侧面是一个圆心角为108°,半径为12cm的扇形,则该圆锥的底面半径是( )
A.1.8cm B.3.6cm C.4cm D.6cm
15.如图,在Rt△ABC 中,∠C=90°,AC=1,BC=,若把△ABC绕边AB所在的直线旋转一周,则所得几何体的表面积为( )
A.(+3)π B.π C.2π D.(2+3)π
16.如图,已知扇形OAB的半径为6cm,圆心角的度数为120°,若将OA,OB重合后围成一圆锥侧面,那么圆锥的底面半径为( )
A.2cm B.3cm C.6cm D.2cm
17.如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4.把△ABC分别绕直线AB,BC和AC旋转一周,所得几何体的表面积分别记作S1,S2,S3,则表面积最大的是( )
A.S1 B.S2 C.S3 D.无法确定
18.圆锥的高是4cm,其底面圆半径为3cm,则它的侧面展开图的面积为( )
A.12πcm2 B.24πcm2 C.15πcm2 D.30πcm2
19.Rt△ABC中,∠C=90°,AC=3,BC=4.把它沿AC所在直线旋转一周,所得几何体的全面积为( )
A.16π B.20π C.36π D.40π
20.如图,在等腰△ABC中,∠BAC=120°,AD是∠BAC的角平分线,且AD=6,以点A为圆心,AD长为半径画弧,交AB于点E,交AC于点F,将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高为( )
A.2 B. C.4 D.
21.如图,圆锥底面半径为r,母线长为20cm,其侧面展开图是圆心角为216°的扇形,则r的值为( )
A.12cm B.15cm C.4πcm D.5πcm
22.如图,已知圆锥的底面半径是2,母线长是6,如果A是底面圆周上一点,从点A拉一根绳子绕圆锥侧面一圈再回到A点,则这根绳子的最短长度是( )
A.8 B.9 C.10 D.6
23.一个底面直径是27厘米,高9厘米的圆锥体木块,分成形状大小完全相同的两个木块后,表面积比原来增加( )
A.81平方厘米 B.243平方匣米
C.121.5平方厘米 D.125.6平方厘米
24.一个圆柱和一个圆锥的底面直径相等,圆锥的高是圆柱的高的2倍,圆锥的体积是8立方分米,圆柱的体积是( )
A.36立方分米 B.12立方分米 C.8立方分米 D.4立方分米
25.一个圆柱的侧面展开正好是一个正方形,这个圆柱的底面直径与高的比是( )
A.1:π B.π:1 C.1:2π D.2π:1
26.若圆锥的底面半径为2cm,侧面展开图的面积为6πcm2,则圆锥的母线长为( )
A.1cm B.2cm C.3cm D.cm
参考答案
1.解:设圆锥底面圆的半径为r,
∵AC=6,∠ACB=120°,
∴==2πr,
∴r=2,即:OA=2,
在Rt△AOC中,OA=2,AC=6,根据勾股定理得,OC==4,
故选:C.
2.解:作OD⊥AB于D,如图,则AD=BD,
∵∠OAD=∠BAC=30°,
∴OD=OA=4cm,AD=OD=4cm,
∴AB=2AD=8cm,
设围成的底面圆的半径为rcm,
则:2πr=,
解得:r=,
故选:D.
3.解:过O作OE⊥AB于E,
∵OA=OB=90cm,∠AOB=120°,
∴∠A=∠B=30°,
∴OE=OA=45cm,
∴弧CD的长==30πcm,
∴圆锥的底面周长为30πcm,
故选:D.
4.解:底面半径是2cm,则底面周长=4πcm,圆锥的侧面积=×4π×3=6πcm2.
故选:B.
5.解:∵圆锥的轴截面是一个斜边为2cm的等腰直角三角形,
∴底面半径=1cm,母线长为cm,底面周长=2πcm,
∴圆锥的侧面积=×2π×=πcm2,
故选:B.
6.解:设扇形的半径为R,
根据题意得:=2πr,
解得:R=2r,
∴圆锥的该为=,
故选:C.
7.解:∵BD平分∠ABC,DA⊥BA,DC⊥BC,
∴∠DBC=∠ABC=30°,DA=DC,
∴∠BDC=60°,
∵以扇形DEC围成的圆锥底面圆半径为1,
∴=2π×1,解得DC=6,
∴DA=6.
故选:C.
8.解:设圆锥的底面的半径为rcm,则DE=2rcm,AE=AB=(9﹣2r)cm,
根据题意得=2πr,
解得r=,
所以AB=9﹣2r=9﹣2×=6(cm).
故选:B.
9.解:设底面圆的半径为R米,
则πR2=25π,解得R=5,
圆锥的母线长==米,
所以圆锥的侧面积= 2π 5 =5π米;
圆柱的侧面积=2π 5 3=30π米2,
所以需要毛毡的面积=(30π+5π)米2.
故选:A.
10.解:∵C为PA的中点,OC=2,
∴AP=2OC=4,
∵PO=6,
∴AO===2,
∴圆锥的侧面积为πrl=π×2×4=24π,
故选:A.
11.解:圆锥侧面展开图的弧长是:2π×1=2π,
设圆心角的度数是n度,
则=2π,
解得:n=120.
故选:C.
12.解:∵2r+l=6,
∴l=6﹣2r,
∴圆锥的侧面积S侧=πrl=πr(6﹣2r)=﹣2π(r2﹣3r)=﹣2π[(r﹣)2﹣]=﹣2π(r﹣)2+π,
∴当r=时,S侧有最大值π.
故选:C.
13.解:设圆锥的底面圆半径为rcm,依题意,得
2πr=,
解得r=10.
故选:B.
14.解:∵扇形的圆心角为108°,半径为12cm,
∴扇形弧长==7.2π(cm),
∴圆锥的底面周长为7.2πcm,
∴圆锥的底面半径==3.6(cm),
故选:B.
15.解:∵Rt△ABC中,∠ACB=90°,AC=1,BC=,
∴AB==2,
设AB边上的高为h,则×2h=×1×,
解得:h=,
∴所得两个圆锥底面半径为.
∴几何体的表面积=×2π××1+×2π××=.
故选:B.
16.解:设这个圆锥的底面圆的半径是rcm,
根据题意得2π r=,
解得r=2,
即这个圆锥的底面圆的半径是2cm.
故选:A.
17.解:∵∠ABC=90°,AB=3,BC=4,
∴AC==5.
△ABC绕直线AB旋转一周,所得几何体为圆锥,底面半径为BC=4,此圆锥的表面积为底面圆面积加扇形表面积,即S1=π×42+π×4×5=36π;
△ABC绕直线BC旋转一周,所得几何体为圆锥,底面半径为AB=3,此圆锥的表面积为底面圆面积加扇形表面积,即S2=π×32+π×3×5=24π;
△ABC绕直线AC旋转一周,所得几何体为两个共底面的圆锥,底面半径为,此圆锥的表面积为两个扇形表面积之和,即S3=π××3+π××4=.
∴S1>S2>S3.
故选:A.
18.解:这个圆锥的母线长==5,
所以这个圆锥的侧面积= 2π 3 5=15π(cm2).
故选:C.
19.解:在Rt△ABC中,∠C=90°,AC=3,BC=4,
∴AB==5,
∵把Rt△ABC绕边AC所在直线旋转一周,
∴所得的几何体的全面积为:底面半径为4,母线长为5的圆锥侧面和半径为4的圆的面积之和,
故π×4×5+π×42=36π.
故选:C.
20.解:设圆锥的底面圆的半径为r,
根据题意得2πr=,解得r=2,
这个圆锥的高h==4,
故选:D.
21.解:∵圆锥底面半径为rcm,母线长为20cm,其侧面展开图是圆心角为216°的扇形,
∴2πr=π×20,
解得r=12.
故选:A.
22.解:连接AC,过B作BD⊥AC于D,
设圆锥侧面展开图的圆心角为n°,
圆锥底面圆周长为2×2π=4π,=,
则n=120,
∵BC=BA,BD⊥AC,
∴∠ABD=60°,
由AB=6,可求得BD=3,∴AD═3,
AC=2AD=6,
即这根绳子的最短长度是6,
故选:D.
23.解:根据题干分析可得,增加部分的表面积为:
27×9÷2×2,
=243÷2×2,
=243(平方厘米),
答:表面积是243平方厘米;
故选:B.
24.解:一个圆柱和一个圆锥的底面直径相等,则它们的底面积就相等,圆柱的体积=底面积×高,
圆锥的体积=×底面积×高,
圆锥的高是圆柱的2倍,所以12立方分米.
故选:B.
25.解:这个圆柱的底面直径与高的比是d:πd=1:π.
故选:A.
26.解:根据圆锥侧面积公式:S=πrl,圆锥的底面半径为2cm,侧面展开图的面积为6πcm2,
故6π=π×2×l,
解得:l=3(cm).
故选:C.
