2021-2022学年鲁教版(五四制)九年级数学下册5.10圆锥的侧面积 填空题专题训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)九年级数学下册5.10圆锥的侧面积 填空题专题训练(Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 188.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 09:58:50 | ||
图片预览




文档简介
2021-2022学年鲁教版九年级数学下册《5.10圆锥的侧面积》填空题专题训练(附答案)
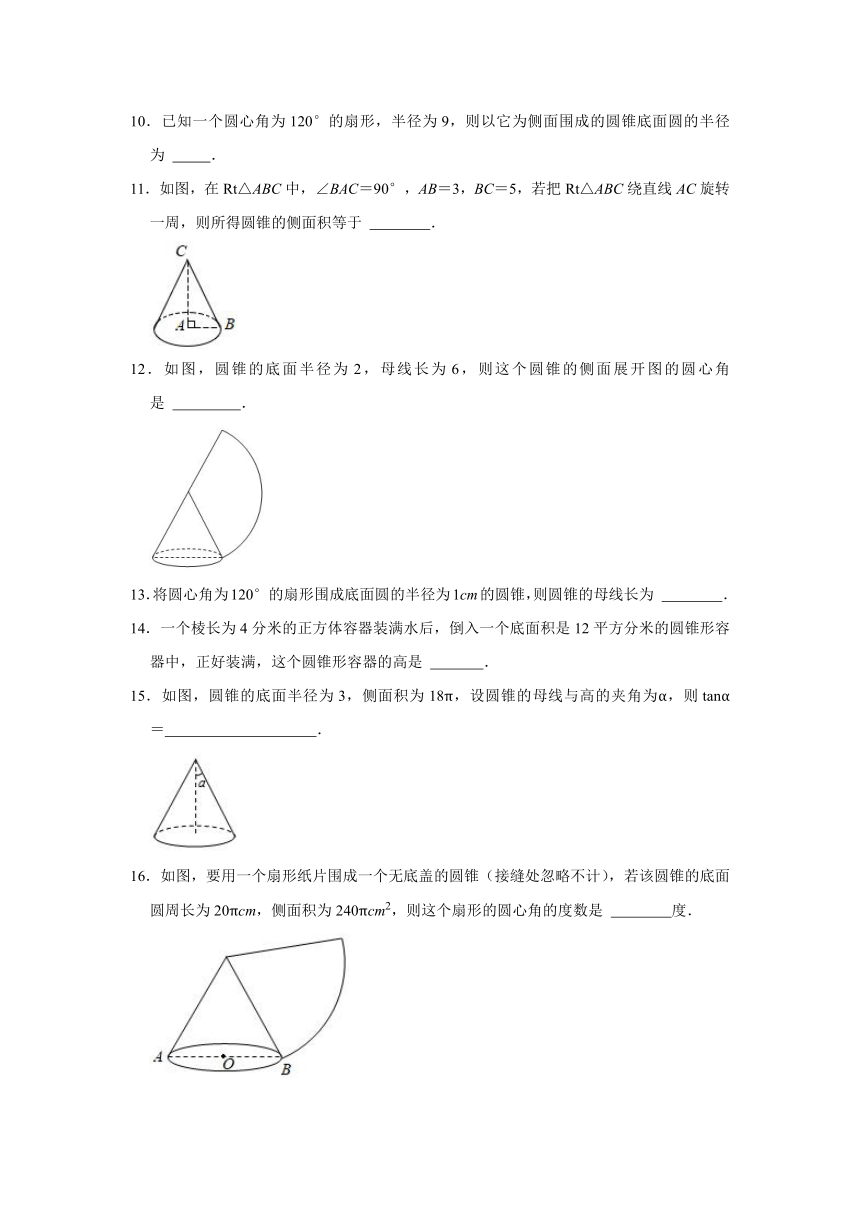
1.已知圆锥的母线长为6cm,侧面积为24cm2,则这个圆锥的底面半径为 cm.
2.将两边长分别是4m和6m的矩形以其一边所在的直线为轴旋转一周,所得的几何体的侧面积是 cm2.
3.一个圆锥的侧面展开图是半圆,则圆锥母线长与底面半径的比为 .
4.数学活动课上,小明制作了一顶圆锥形纸帽(如图),其底面直径为24cm,母线长为20cm,将这顶纸帽剪开,展开成扇形时圆心角的度数为 度.
5.如图,圆锥的底面半径OB=6,高OC=8,则圆锥的侧面积等于
6.如图,粮仓由筒仓(圆柱)和仓顶(圆锥)组合而成,则该粮仓仓顶的表面积为 m2(结果保留π).
7.用一个圆心角为90°,半径为6的扇形做一个圆锥侧面,则这个圆锥底面圆面积为 .
8.用半径为6,圆心角为90°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆的半径为 .
9.如图,小明用一个半径为12cm,面积为24πcm2的扇形纸板,制作一个圆锥形的玩具帽,则帽子的底面半径R= .
10.已知一个圆心角为120°的扇形,半径为9,则以它为侧面围成的圆锥底面圆的半径为 .
11.如图,在Rt△ABC中,∠BAC=90°,AB=3,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的侧面积等于 .
12.如图,圆锥的底面半径为2,母线长为6,则这个圆锥的侧面展开图的圆心角是 .
13.将圆心角为120°的扇形围成底面圆的半径为1cm的圆锥,则圆锥的母线长为 .
14.一个棱长为4分米的正方体容器装满水后,倒入一个底面积是12平方分米的圆锥形容器中,正好装满,这个圆锥形容器的高是 .
15.如图,圆锥的底面半径为3,侧面积为18π,设圆锥的母线与高的夹角为α,则tanα= .
16.如图,要用一个扇形纸片围成一个无底盖的圆锥(接缝处忽略不计),若该圆锥的底面圆周长为20πcm,侧面积为240πcm2,则这个扇形的圆心角的度数是 度.
17.如图是一个圆锥形冰淇淋外壳.(不计厚度)已知其母线长为12cm,底面圆的半径为3cm,则这个冰淇淋外壳的侧面积等于 cm2.
18.如图,在2×2的正方形网格中,每个小正方形的边长为1.以点O为圆心、2为半径画弧,交图中网格线于点A、B,则扇形OAB围成圆锥的底面半径为 .
19.如图,已知圆锥底面半径是2,母线长是6.如果A是底面圆周上一点,从点A拉一根绳子绕圆锥侧面一圈再回到A点,则这根绳子的最短长度是 .
20.已知圆锥的母线长为10,高为8,则该圆锥的侧面展开图(扇形)的弧长为 .(用含π的代数式表示),圆心角为 度.
21.用一块弧长16πcm的扇形铁片,做一个高为6cm的圆锥形工件侧面(接缝忽略不计),那么这个扇形铁片的面积为 cm2.
22.如图,扇形的半径为6,圆心角θ为120°,用这个扇形围成一个圆锥的侧面,所得圆的底面半径为 .
23.如图,一把遮阳伞撑开时母线的长是3m,底面半径为2m,则做这把遮阳伞需用布料的面积是 m2.
24.在如图所示的网格中,每个小正方形的边长为1,每个小正方形的顶点叫做格点,点O、A、B都是格点,若图中扇形AOB是一个圆锥的侧面展开图,则该圆锥底面圆的半径为 .
25.电焊工用一个圆心角为120°,半径为24cm的扇形白铁片制作一个圆锥的侧面(假设焊接时缝隙宽度忽略不计),则这个圆锥的底面半径为 cm.
26.如图,从直径为的圆形纸片上剪出一个圆心角为90°的扇形ABC.使点A、B、C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面半径是 .
参考答案
1.解:设圆锥的底面半径为rcm,
∵圆锥的母线长是6cm,侧面积是24πcm2,
∴24π=π r 6,
∴r=4,
故答案为:4.
2.解:这个长方形绕一边所在直线旋转一周后是圆柱.
当把矩形6m的一边所在直线为轴旋转一周,那么圆柱的底面半径为4m,高为6m,
∴圆柱的侧面积为4π×2×6=48π(m2)=480000π(cm2);
当把矩形4m的一边所在直线为轴旋转一周,那么圆柱的底面半径为6m,高为4m,
∴圆柱的侧面积为6π×2×4=48π(m2)=480000π(cm2);
故答案为480000π.
3.解:设圆锥的母线长为R,底面半径为r,
∵圆锥的侧面展开图是一个半圆,
∴圆锥的侧面展开扇形的弧长为:πR,
∵圆锥的侧面展开扇形的周长等于圆锥的底面周长,
∵πR=2πr,
∴R:r=2:1,
故答案为:2:1.
4.解:设展开扇形的度数为n°,
由图知圆锥的底面直径为24cm,母线长为20cm,
∵圆锥的侧面展开扇形的弧长等于圆锥的底面周长,
∴24π=,
解得n=216.
故答案为:216.
5.解:∵它的底面半径OB=6,高OC=8.
∴BC==10,
∴这个圆锥漏斗的侧面积是:πrl=π×6×10=60π.
故答案为:60π.
6.解:圆锥的高为7﹣4=3(m),
所以圆锥的母线长为=3(m),
所以该粮仓仓顶的表面积=×2π×3×3=9(m2).
故答案为9.
7.解:设这个圆锥的底面圆的半径为r,
根据题意得2πr=,解得r=,
所以这个圆锥的底面圆的面积=π×()2=π.
故答案为π.
8.解:设这个圆锥的底面圆半径为r,
根据题意得2πr=,
解得r=1.5,
所以这个圆锥的底面圆半径为1.5.
故答案为1.5.
9.解:由扇形的面积公式得,扇形面积S=πr×12=24π,
∴r=2,
故答案为:2cm.
10.解:圆锥的底面周长是:=6π.
设圆锥底面圆的半径是r,则2πr=6π.
解得:r=3.
故答案是:3.
11.解:∵AB=3,
∴底面的周长是:6π
∴圆锥的侧面积等×6π×5=15π,
故答案为:15π.
12.解:圆锥侧面展开图的弧长是:2π×2=4π,
设圆心角的度数是n度.则=4π,
解得:n=120.
故答案为:120°.
13.解:设圆锥的母线长为l,
根据题意得:
解得l=3cm.
故答案为:3cm.
14.解:设圆锥形容器的高为x分米,
由题意得:×12×x=43,
解得:x=16,
则这个圆锥形容器的高是16分米,
故答案为:16.
15.解:如图,由题意可知OA=3,S扇形SAB=18π,
的长l=2π×3=6π,
∵S扇形SAB=18π,
∴×6π×R=18π,
∴R=6,
即SA=6,在Rt△SOA中,SA=6,OA=3,
∴SO===3,
∴tanα===,
故答案为:.
16.解:设圆锥的母线长为lcm,扇形的圆心角为n°,
∵圆锥的底面圆周长为20πcm,
∴圆锥的侧面展开图扇形的弧长为20πcm,
由题意得:×20π×l=240π,
解得:l=24,
则=20π,
解得,n=150,即扇形的圆心角为150°,
故答案为:150.
17.解:∵底面圆的半径为3cm,
∴底面圆的周长为6π(cm),即圆锥侧面展开图扇形的弧长为6πcm,
∴这个冰淇淋外壳的侧面积=×12×6π=36π(cm2)
故答案为:36π.
18.解:连接OB,过B点的水平格线与OA交于点C,如图,
∵OA=OB=2,OC=1,
∴cos∠BOC==,
∴∠BOC=60°,
设扇形OAB围成圆锥的底面半径为r,
∴2πr=,解得r=,
即扇形OAB围成圆锥的底面半径为.
故答案为.
19.解:设∠ABC=n°,
∴底面圆的周长等于:2π×2=,
解得:n=120°;
连接AC,过B作BD⊥AC于D,
则∠ABD=60°.
∵AB=6,
∴BD=3,
∴AD═3×=9,
∴AC=2AD=18,
即这根绳子的最短长度是18.
故答案为:18.
20.解:设底面圆的半径为rcm,
由勾股定理得:r==6,
∴2πr=2π×6=12π,
根据题意得2π×6=,
解得n=216,
即这个圆锥的侧面展开图的圆心角为216°.
故答案为:12π,216.
21.解:∵扇形铁片的弧长16πcm,
∴圆锥的底面周长为16πcm,
∴圆锥的底面半径==8(cm),
由勾股定理得:圆锥的母线长==10(cm),
∴扇形铁片的面积=×16π×10=80π(cm2)
故答案为:80π.
22.解:扇形的弧长为=4π,即圆锥底面周长为4π,
所以底面半径为4π÷2π=2,
故答案为:2.
23.解:做这把遮阳伞需用布料的面积=×2π×2×3=6π(m2).
故答案为:6π.
24.解:设该圆锥底面圆的半径为r.
∵每个小方格都是边长为1的正方形,
∴AO==5,
∵∠AOB=90°,
∴=2πr,
∴r=.
故答案是:.
25.解:设这个圆锥的底面半径为rcm,
根据题意得2πr=,
解得r=8.
答:这个圆锥的底面半径为8cm.
故答案为8.
26.解:连接BC,如图,
∵∠BAC=90°,
∴BC为⊙O的直径,即BC=8,
∴AB=BC=8,
设这个圆锥的底面半径为r,
根据题意得2πr=,
解得r=2,
即这个圆锥的底面半径为2.
故答案为2.
1.已知圆锥的母线长为6cm,侧面积为24cm2,则这个圆锥的底面半径为 cm.
2.将两边长分别是4m和6m的矩形以其一边所在的直线为轴旋转一周,所得的几何体的侧面积是 cm2.
3.一个圆锥的侧面展开图是半圆,则圆锥母线长与底面半径的比为 .
4.数学活动课上,小明制作了一顶圆锥形纸帽(如图),其底面直径为24cm,母线长为20cm,将这顶纸帽剪开,展开成扇形时圆心角的度数为 度.
5.如图,圆锥的底面半径OB=6,高OC=8,则圆锥的侧面积等于
6.如图,粮仓由筒仓(圆柱)和仓顶(圆锥)组合而成,则该粮仓仓顶的表面积为 m2(结果保留π).
7.用一个圆心角为90°,半径为6的扇形做一个圆锥侧面,则这个圆锥底面圆面积为 .
8.用半径为6,圆心角为90°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆的半径为 .
9.如图,小明用一个半径为12cm,面积为24πcm2的扇形纸板,制作一个圆锥形的玩具帽,则帽子的底面半径R= .
10.已知一个圆心角为120°的扇形,半径为9,则以它为侧面围成的圆锥底面圆的半径为 .
11.如图,在Rt△ABC中,∠BAC=90°,AB=3,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的侧面积等于 .
12.如图,圆锥的底面半径为2,母线长为6,则这个圆锥的侧面展开图的圆心角是 .
13.将圆心角为120°的扇形围成底面圆的半径为1cm的圆锥,则圆锥的母线长为 .
14.一个棱长为4分米的正方体容器装满水后,倒入一个底面积是12平方分米的圆锥形容器中,正好装满,这个圆锥形容器的高是 .
15.如图,圆锥的底面半径为3,侧面积为18π,设圆锥的母线与高的夹角为α,则tanα= .
16.如图,要用一个扇形纸片围成一个无底盖的圆锥(接缝处忽略不计),若该圆锥的底面圆周长为20πcm,侧面积为240πcm2,则这个扇形的圆心角的度数是 度.
17.如图是一个圆锥形冰淇淋外壳.(不计厚度)已知其母线长为12cm,底面圆的半径为3cm,则这个冰淇淋外壳的侧面积等于 cm2.
18.如图,在2×2的正方形网格中,每个小正方形的边长为1.以点O为圆心、2为半径画弧,交图中网格线于点A、B,则扇形OAB围成圆锥的底面半径为 .
19.如图,已知圆锥底面半径是2,母线长是6.如果A是底面圆周上一点,从点A拉一根绳子绕圆锥侧面一圈再回到A点,则这根绳子的最短长度是 .
20.已知圆锥的母线长为10,高为8,则该圆锥的侧面展开图(扇形)的弧长为 .(用含π的代数式表示),圆心角为 度.
21.用一块弧长16πcm的扇形铁片,做一个高为6cm的圆锥形工件侧面(接缝忽略不计),那么这个扇形铁片的面积为 cm2.
22.如图,扇形的半径为6,圆心角θ为120°,用这个扇形围成一个圆锥的侧面,所得圆的底面半径为 .
23.如图,一把遮阳伞撑开时母线的长是3m,底面半径为2m,则做这把遮阳伞需用布料的面积是 m2.
24.在如图所示的网格中,每个小正方形的边长为1,每个小正方形的顶点叫做格点,点O、A、B都是格点,若图中扇形AOB是一个圆锥的侧面展开图,则该圆锥底面圆的半径为 .
25.电焊工用一个圆心角为120°,半径为24cm的扇形白铁片制作一个圆锥的侧面(假设焊接时缝隙宽度忽略不计),则这个圆锥的底面半径为 cm.
26.如图,从直径为的圆形纸片上剪出一个圆心角为90°的扇形ABC.使点A、B、C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面半径是 .
参考答案
1.解:设圆锥的底面半径为rcm,
∵圆锥的母线长是6cm,侧面积是24πcm2,
∴24π=π r 6,
∴r=4,
故答案为:4.
2.解:这个长方形绕一边所在直线旋转一周后是圆柱.
当把矩形6m的一边所在直线为轴旋转一周,那么圆柱的底面半径为4m,高为6m,
∴圆柱的侧面积为4π×2×6=48π(m2)=480000π(cm2);
当把矩形4m的一边所在直线为轴旋转一周,那么圆柱的底面半径为6m,高为4m,
∴圆柱的侧面积为6π×2×4=48π(m2)=480000π(cm2);
故答案为480000π.
3.解:设圆锥的母线长为R,底面半径为r,
∵圆锥的侧面展开图是一个半圆,
∴圆锥的侧面展开扇形的弧长为:πR,
∵圆锥的侧面展开扇形的周长等于圆锥的底面周长,
∵πR=2πr,
∴R:r=2:1,
故答案为:2:1.
4.解:设展开扇形的度数为n°,
由图知圆锥的底面直径为24cm,母线长为20cm,
∵圆锥的侧面展开扇形的弧长等于圆锥的底面周长,
∴24π=,
解得n=216.
故答案为:216.
5.解:∵它的底面半径OB=6,高OC=8.
∴BC==10,
∴这个圆锥漏斗的侧面积是:πrl=π×6×10=60π.
故答案为:60π.
6.解:圆锥的高为7﹣4=3(m),
所以圆锥的母线长为=3(m),
所以该粮仓仓顶的表面积=×2π×3×3=9(m2).
故答案为9.
7.解:设这个圆锥的底面圆的半径为r,
根据题意得2πr=,解得r=,
所以这个圆锥的底面圆的面积=π×()2=π.
故答案为π.
8.解:设这个圆锥的底面圆半径为r,
根据题意得2πr=,
解得r=1.5,
所以这个圆锥的底面圆半径为1.5.
故答案为1.5.
9.解:由扇形的面积公式得,扇形面积S=πr×12=24π,
∴r=2,
故答案为:2cm.
10.解:圆锥的底面周长是:=6π.
设圆锥底面圆的半径是r,则2πr=6π.
解得:r=3.
故答案是:3.
11.解:∵AB=3,
∴底面的周长是:6π
∴圆锥的侧面积等×6π×5=15π,
故答案为:15π.
12.解:圆锥侧面展开图的弧长是:2π×2=4π,
设圆心角的度数是n度.则=4π,
解得:n=120.
故答案为:120°.
13.解:设圆锥的母线长为l,
根据题意得:
解得l=3cm.
故答案为:3cm.
14.解:设圆锥形容器的高为x分米,
由题意得:×12×x=43,
解得:x=16,
则这个圆锥形容器的高是16分米,
故答案为:16.
15.解:如图,由题意可知OA=3,S扇形SAB=18π,
的长l=2π×3=6π,
∵S扇形SAB=18π,
∴×6π×R=18π,
∴R=6,
即SA=6,在Rt△SOA中,SA=6,OA=3,
∴SO===3,
∴tanα===,
故答案为:.
16.解:设圆锥的母线长为lcm,扇形的圆心角为n°,
∵圆锥的底面圆周长为20πcm,
∴圆锥的侧面展开图扇形的弧长为20πcm,
由题意得:×20π×l=240π,
解得:l=24,
则=20π,
解得,n=150,即扇形的圆心角为150°,
故答案为:150.
17.解:∵底面圆的半径为3cm,
∴底面圆的周长为6π(cm),即圆锥侧面展开图扇形的弧长为6πcm,
∴这个冰淇淋外壳的侧面积=×12×6π=36π(cm2)
故答案为:36π.
18.解:连接OB,过B点的水平格线与OA交于点C,如图,
∵OA=OB=2,OC=1,
∴cos∠BOC==,
∴∠BOC=60°,
设扇形OAB围成圆锥的底面半径为r,
∴2πr=,解得r=,
即扇形OAB围成圆锥的底面半径为.
故答案为.
19.解:设∠ABC=n°,
∴底面圆的周长等于:2π×2=,
解得:n=120°;
连接AC,过B作BD⊥AC于D,
则∠ABD=60°.
∵AB=6,
∴BD=3,
∴AD═3×=9,
∴AC=2AD=18,
即这根绳子的最短长度是18.
故答案为:18.
20.解:设底面圆的半径为rcm,
由勾股定理得:r==6,
∴2πr=2π×6=12π,
根据题意得2π×6=,
解得n=216,
即这个圆锥的侧面展开图的圆心角为216°.
故答案为:12π,216.
21.解:∵扇形铁片的弧长16πcm,
∴圆锥的底面周长为16πcm,
∴圆锥的底面半径==8(cm),
由勾股定理得:圆锥的母线长==10(cm),
∴扇形铁片的面积=×16π×10=80π(cm2)
故答案为:80π.
22.解:扇形的弧长为=4π,即圆锥底面周长为4π,
所以底面半径为4π÷2π=2,
故答案为:2.
23.解:做这把遮阳伞需用布料的面积=×2π×2×3=6π(m2).
故答案为:6π.
24.解:设该圆锥底面圆的半径为r.
∵每个小方格都是边长为1的正方形,
∴AO==5,
∵∠AOB=90°,
∴=2πr,
∴r=.
故答案是:.
25.解:设这个圆锥的底面半径为rcm,
根据题意得2πr=,
解得r=8.
答:这个圆锥的底面半径为8cm.
故答案为8.
26.解:连接BC,如图,
∵∠BAC=90°,
∴BC为⊙O的直径,即BC=8,
∴AB=BC=8,
设这个圆锥的底面半径为r,
根据题意得2πr=,
解得r=2,
即这个圆锥的底面半径为2.
故答案为2.
