2021-2022学年人教版八年级数学上册15.2分式的运算 优生辅导训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册15.2分式的运算 优生辅导训练(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 150.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 00:00:00 | ||
图片预览


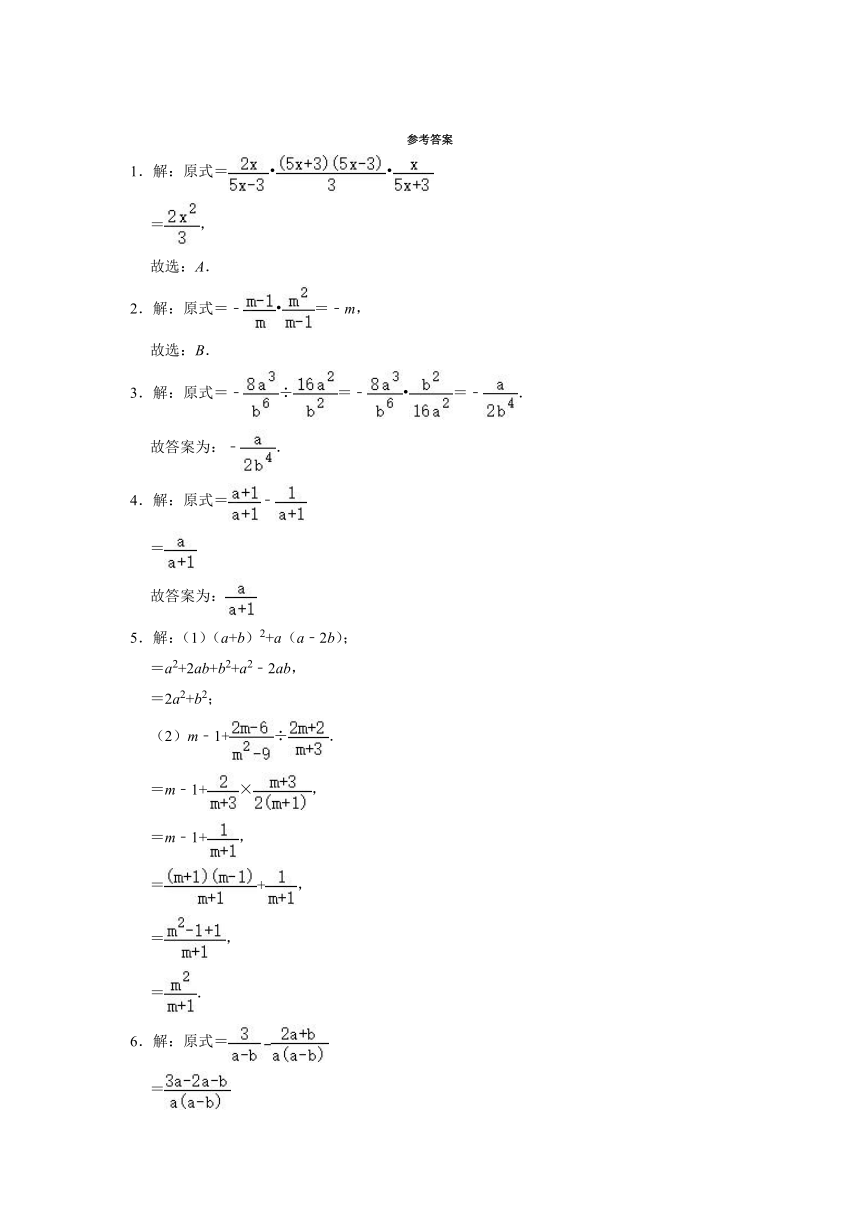
文档简介
2021-2022学年人教版八年级数学上册《15.2分式的运算》优生辅导训练(附答案)
1.计算的结果为( )
A. B. C. D.
2.化简÷是( )
A.m B.﹣m C. D.﹣
3.计算(﹣)3÷(﹣)2的结果是 .
4.计算1﹣= .
5.计算:
(1)(a+b)2+a(a﹣2b);
(2)m﹣1+÷.
6.计算:.
7.计算:﹣.
8.上课时老师在黑板上书写了一个分式的正确化简结果,随后用手掌盖住了一部分,形式如下:
﹣=
(1)聪明的你请求出盖住部分化简后的结果;
(2)当x=2时,y等于何值时,原分式的值为5.
9.计算:
(1)(﹣3xy)÷ ()2;
(2)(﹣)÷ (+).
10.先化简,再求值:(x﹣2+)÷,其中x=﹣.
11.先化简,再求值:﹣,其中a=﹣5.
12.已知x2﹣4=0,求代数式(﹣)÷+2020的值.
13.小明学习了“第八章 幂的运算”后做这样一道题:若(2x﹣3)x+3=1,求x的值,他解出来的结果为x=1,老师说小明考虑问题不全面,聪明的你能帮助小明解决这个问题吗?
小明解答过程如下:
解:因为1的任何次幂为1,所以2x﹣3=1,x=2.且2+3=5
故(2x﹣3)x+3=(2×2﹣3)2+3=15=1,所以x=2
你的解答是:
14.甲工程队完成一项工程需要n天(n>1),乙工程队完成这项工程的时间是甲工程队的2倍多1天,则甲队的工作效率是乙队的3倍吗?请说明理由.
15.甲、乙两位采购员同去购买两次饲料.两次饲料的价格有变化,分别为m元/千克和n元/千克(m,n是正数,且m≠n),两位采购员的购货方式也不同,其中甲每次购买1000千克,乙每次用去1000元.
(1)甲、乙所购饲料的平均单价各是多少?
(2)谁的购货方式更合算?
16.有编号为①、②、③、④的四条赛艇,其速度依次为每小时v1、v2、v3、v4千米,且满足v1>v2>v3>v4>0,其中,v水为河流的水流速度(千米/小时),它们在河流中进行追逐赛规则如下:(1)四条艇在同一起跑线上,同时出发,①、②、③是逆流而上,④号艇顺流而下.(2)经过1小时,①、②、③同时掉头,追赶④号艇,谁先追上④号艇谁为冠军,问冠军为几号艇?
17.某工厂库存原材料x吨,原计划每天用a吨,若现在每天少用b吨,则可以多用多少天?
18.学校有一块面积为m的操场,七年级(2)班的a位同学承担了清除操场杂草的任务.若平均每位同学每小时能清除面积为n的杂草,则全班清除全部杂草需要多少时间?七年级(1)班有b位同学,若平均每位同学每小时能清除面积为k的杂草,则两班合作要比七年级(2)班单独完成提前多少时间?
19.一项工程,甲单独做x天完成,乙单独做需y天完成.
(1)甲乙合作,需多少天完成?
(2)工程完成后共得劳动报酬m元,甲乙应各分得多少元?
20.某村种植甲种玉米a公顷和乙种玉米b公顷,总产量为x千克;水稻的种植面积比玉米少2b公顷,总产量比玉米的2倍少y千克,写出表示玉米和水稻的单位面积产量(单位:千克/公顷)的式子.如果两式的分母不相同,进行通分.
参考答案
1.解:原式=
=,
故选:A.
2.解:原式=﹣ =﹣m,
故选:B.
3.解:原式=﹣÷=﹣ =﹣.
故答案为:﹣.
4.解:原式=﹣
=
故答案为:
5.解:(1)(a+b)2+a(a﹣2b);
=a2+2ab+b2+a2﹣2ab,
=2a2+b2;
(2)m﹣1+÷.
=m﹣1+×,
=m﹣1+,
=+,
=,
=.
6.解:原式=
=
=
=.
7.解:原式==3.
8.解:(1)∵(+)÷
=[+]×
=×
=﹣
∴盖住部分化简后的结果为﹣;
(2)∵x=2时,原分式的值为5,
即,
∴10﹣5y=2
解得y=
经检验,y=是原方程的解.
所以当x=2,y=时,原分式的值为5.
9.解:(1)原式=(﹣3xy)÷
=(﹣3xy)
=﹣;
(2)原式=÷
=
=1.
10.解:原式=(+)
=
=2(x+2)
=2x+4,
当x=﹣时,
原式=2×(﹣)+4
=﹣1+4
=3.
11.解:原式= ﹣
=﹣
=﹣,
当a=﹣5时,
原式=﹣=1.
12.解:原式=[﹣]÷+2020
=(﹣) +2020
= +2020
=x+3+2020
=x+2023,
∵x2﹣4=0,
∴x=2或x=﹣2,
又x≠2且x≠3,
∴x=﹣2,
则原式=﹣2+2023=2021.
13.解:①∵1的任何次幂为1,所以2x﹣3=1,x=2.且2+3=5,
∴(2x﹣3)x+3=(2×2﹣3)2+3=15=1,
∴x=2;
②∵﹣1的任何偶次幂也都是1,
∴2x﹣3=﹣1,且x+3为偶数,
∴x=1,
当x=1时,x+3=4是偶数,
∴x=1;
③∵任何不是0的数的0次幂也是1,
∴x+3=0,2x﹣3≠0,
解的:x=﹣3,
综上:x=2或﹣3或1.
14.解:甲队的工作效率不是乙队的3倍.
甲的工作效率:,
乙的工作效率:,
甲队的工作效率是乙队的÷=(倍),
∵n>1,
∴<3,
∴甲队的工作效率不是乙队的3倍.
15.解:(1)根据题意得:
甲所购饲料的平均单价是:=(元/千克);
乙所购饲料的平均单价是:=(元/千克);
(2)∵﹣
=
=
又m≠n,
∴(m﹣n)2>0,
∴﹣>0,
∴乙的购买方式更合算.
16.解:出发1小时后,①、②、③号艇与④号艇的距离分别为Si=[(vi﹣v水)+(v水+v4)]×1=vi+v4,
各艇追上④号艇的时间为,
∵v1>v2>v3>v4,
∴t1<t2<t3.
即①号艇追上④号艇用的时间最小,①号是冠军.
17.解:依题意得可多用天数为:﹣=天.
答:可多用天.
18.解:由题意得七(2)班清除全部杂草需要时间为(小时);
两班合作要比七年级(2)班单独完成提前(小时).
19.解:(1)解;∵甲单独完成需要x天,乙单独完成需要y天,
∴甲单独完成的工作效率是,乙单独完成的工作效率是,
∴两人合作需要的时间为:1÷()=;
∴甲乙合作,需要天;
(2)∵甲单独完成的工作效率是,乙单独完成的工作效率是,
∴工程完成后,甲完成,应分得(元),
乙完成,应分得(元).
20.解:依题意得
玉米的单位面积产量是:=.
水稻的单位面积产量是:==.
答:玉米和水稻的单位面积产量分别是千克/公顷、千克/公顷.
1.计算的结果为( )
A. B. C. D.
2.化简÷是( )
A.m B.﹣m C. D.﹣
3.计算(﹣)3÷(﹣)2的结果是 .
4.计算1﹣= .
5.计算:
(1)(a+b)2+a(a﹣2b);
(2)m﹣1+÷.
6.计算:.
7.计算:﹣.
8.上课时老师在黑板上书写了一个分式的正确化简结果,随后用手掌盖住了一部分,形式如下:
﹣=
(1)聪明的你请求出盖住部分化简后的结果;
(2)当x=2时,y等于何值时,原分式的值为5.
9.计算:
(1)(﹣3xy)÷ ()2;
(2)(﹣)÷ (+).
10.先化简,再求值:(x﹣2+)÷,其中x=﹣.
11.先化简,再求值:﹣,其中a=﹣5.
12.已知x2﹣4=0,求代数式(﹣)÷+2020的值.
13.小明学习了“第八章 幂的运算”后做这样一道题:若(2x﹣3)x+3=1,求x的值,他解出来的结果为x=1,老师说小明考虑问题不全面,聪明的你能帮助小明解决这个问题吗?
小明解答过程如下:
解:因为1的任何次幂为1,所以2x﹣3=1,x=2.且2+3=5
故(2x﹣3)x+3=(2×2﹣3)2+3=15=1,所以x=2
你的解答是:
14.甲工程队完成一项工程需要n天(n>1),乙工程队完成这项工程的时间是甲工程队的2倍多1天,则甲队的工作效率是乙队的3倍吗?请说明理由.
15.甲、乙两位采购员同去购买两次饲料.两次饲料的价格有变化,分别为m元/千克和n元/千克(m,n是正数,且m≠n),两位采购员的购货方式也不同,其中甲每次购买1000千克,乙每次用去1000元.
(1)甲、乙所购饲料的平均单价各是多少?
(2)谁的购货方式更合算?
16.有编号为①、②、③、④的四条赛艇,其速度依次为每小时v1、v2、v3、v4千米,且满足v1>v2>v3>v4>0,其中,v水为河流的水流速度(千米/小时),它们在河流中进行追逐赛规则如下:(1)四条艇在同一起跑线上,同时出发,①、②、③是逆流而上,④号艇顺流而下.(2)经过1小时,①、②、③同时掉头,追赶④号艇,谁先追上④号艇谁为冠军,问冠军为几号艇?
17.某工厂库存原材料x吨,原计划每天用a吨,若现在每天少用b吨,则可以多用多少天?
18.学校有一块面积为m的操场,七年级(2)班的a位同学承担了清除操场杂草的任务.若平均每位同学每小时能清除面积为n的杂草,则全班清除全部杂草需要多少时间?七年级(1)班有b位同学,若平均每位同学每小时能清除面积为k的杂草,则两班合作要比七年级(2)班单独完成提前多少时间?
19.一项工程,甲单独做x天完成,乙单独做需y天完成.
(1)甲乙合作,需多少天完成?
(2)工程完成后共得劳动报酬m元,甲乙应各分得多少元?
20.某村种植甲种玉米a公顷和乙种玉米b公顷,总产量为x千克;水稻的种植面积比玉米少2b公顷,总产量比玉米的2倍少y千克,写出表示玉米和水稻的单位面积产量(单位:千克/公顷)的式子.如果两式的分母不相同,进行通分.
参考答案
1.解:原式=
=,
故选:A.
2.解:原式=﹣ =﹣m,
故选:B.
3.解:原式=﹣÷=﹣ =﹣.
故答案为:﹣.
4.解:原式=﹣
=
故答案为:
5.解:(1)(a+b)2+a(a﹣2b);
=a2+2ab+b2+a2﹣2ab,
=2a2+b2;
(2)m﹣1+÷.
=m﹣1+×,
=m﹣1+,
=+,
=,
=.
6.解:原式=
=
=
=.
7.解:原式==3.
8.解:(1)∵(+)÷
=[+]×
=×
=﹣
∴盖住部分化简后的结果为﹣;
(2)∵x=2时,原分式的值为5,
即,
∴10﹣5y=2
解得y=
经检验,y=是原方程的解.
所以当x=2,y=时,原分式的值为5.
9.解:(1)原式=(﹣3xy)÷
=(﹣3xy)
=﹣;
(2)原式=÷
=
=1.
10.解:原式=(+)
=
=2(x+2)
=2x+4,
当x=﹣时,
原式=2×(﹣)+4
=﹣1+4
=3.
11.解:原式= ﹣
=﹣
=﹣,
当a=﹣5时,
原式=﹣=1.
12.解:原式=[﹣]÷+2020
=(﹣) +2020
= +2020
=x+3+2020
=x+2023,
∵x2﹣4=0,
∴x=2或x=﹣2,
又x≠2且x≠3,
∴x=﹣2,
则原式=﹣2+2023=2021.
13.解:①∵1的任何次幂为1,所以2x﹣3=1,x=2.且2+3=5,
∴(2x﹣3)x+3=(2×2﹣3)2+3=15=1,
∴x=2;
②∵﹣1的任何偶次幂也都是1,
∴2x﹣3=﹣1,且x+3为偶数,
∴x=1,
当x=1时,x+3=4是偶数,
∴x=1;
③∵任何不是0的数的0次幂也是1,
∴x+3=0,2x﹣3≠0,
解的:x=﹣3,
综上:x=2或﹣3或1.
14.解:甲队的工作效率不是乙队的3倍.
甲的工作效率:,
乙的工作效率:,
甲队的工作效率是乙队的÷=(倍),
∵n>1,
∴<3,
∴甲队的工作效率不是乙队的3倍.
15.解:(1)根据题意得:
甲所购饲料的平均单价是:=(元/千克);
乙所购饲料的平均单价是:=(元/千克);
(2)∵﹣
=
=
又m≠n,
∴(m﹣n)2>0,
∴﹣>0,
∴乙的购买方式更合算.
16.解:出发1小时后,①、②、③号艇与④号艇的距离分别为Si=[(vi﹣v水)+(v水+v4)]×1=vi+v4,
各艇追上④号艇的时间为,
∵v1>v2>v3>v4,
∴t1<t2<t3.
即①号艇追上④号艇用的时间最小,①号是冠军.
17.解:依题意得可多用天数为:﹣=天.
答:可多用天.
18.解:由题意得七(2)班清除全部杂草需要时间为(小时);
两班合作要比七年级(2)班单独完成提前(小时).
19.解:(1)解;∵甲单独完成需要x天,乙单独完成需要y天,
∴甲单独完成的工作效率是,乙单独完成的工作效率是,
∴两人合作需要的时间为:1÷()=;
∴甲乙合作,需要天;
(2)∵甲单独完成的工作效率是,乙单独完成的工作效率是,
∴工程完成后,甲完成,应分得(元),
乙完成,应分得(元).
20.解:依题意得
玉米的单位面积产量是:=.
水稻的单位面积产量是:==.
答:玉米和水稻的单位面积产量分别是千克/公顷、千克/公顷.
