2021-2022学年冀教版八年级数学上册16.2线段的垂直平分线 同步达标测评(Word版含答案)
文档属性
| 名称 | 2021-2022学年冀教版八年级数学上册16.2线段的垂直平分线 同步达标测评(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 294.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 10:05:40 | ||
图片预览



文档简介
2021-2022学年冀教版八年级数学上册《16.2线段的垂直平分线》同步达标测评(附答案)
一.选择题(共10小题,满分40分)
1.如图,△ABC中,AB=10,边BC的垂直平分线DE分别交AB、BC于E、D,且AC=6,则△ACE的周长为( )
A.16 B.18 C.22 D.26
2.在Rt△ABC中,∠C=90°,有一点D同时满足以下三个条件:①在直角边BC上;②在∠CAB的角平分线上;③在斜边AB的垂直平分线上,那么∠B为( )
A.15° B.30° C.45° D.60°
3.如图,∠ABC=90°,∠C=15°,线段AC的垂直平分线DE交AC于D,交BC于E,D为垂足,CE=10 cm,则AB=( )
A.4 cm B.5 cm C.6 cm D.不能确定
4.如图,在△ABC中,PM、QN分别是线段AB、AC的垂直平分线,若∠BAC=110°,则∠PAQ的度数是( )
A.40° B.50° C.60° D.70°
5.如图,在△ABC中,AB边的中垂线DE,分别与AB、AC边交于点D、E两点,BC边的中垂线FG,分别与BC、AC边交于点F、G两点,连接BE、BG.若△BEG的周长为16,GE=1.则AC的长为( )
A.13 B.14 C.15 D.16
6.如图,在△ABC中,∠A=120°,AB、AC边上的中垂线DE、DF交于点D,垂足分别为点E、F,DE、DF分别交BC于点M、N,连接BD,CD.下列结论:①∠EDF=60°;②DB=DC;③MN=DN;④∠ABC=∠FDC.其中正确的结论是( )
A.①③④ B.①②③ C.②③④ D.①②④
7.如图,△ABC中,∠B=35°,∠BAC的平分线AD交BC于点D,若DE垂直平分AB,则∠C的度数为( )
A.80° B.75° C.65° D.60°
8.如图,△ABC中,BD平分∠ABC,E是BC的中点,过点E作BC的垂线交BD于点F,连接CF,若∠DFC=60°,∠ACF=40°,则∠A的度数为( )
A.45° B.50° C.55° D.60°
9.如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点D,交AB于点E,连接AD,AD将∠CAB分成两个角,且∠CAD:∠BAD=2:5,则∠ADC的度数是( )
A.70° B.75° C.80° D.85°
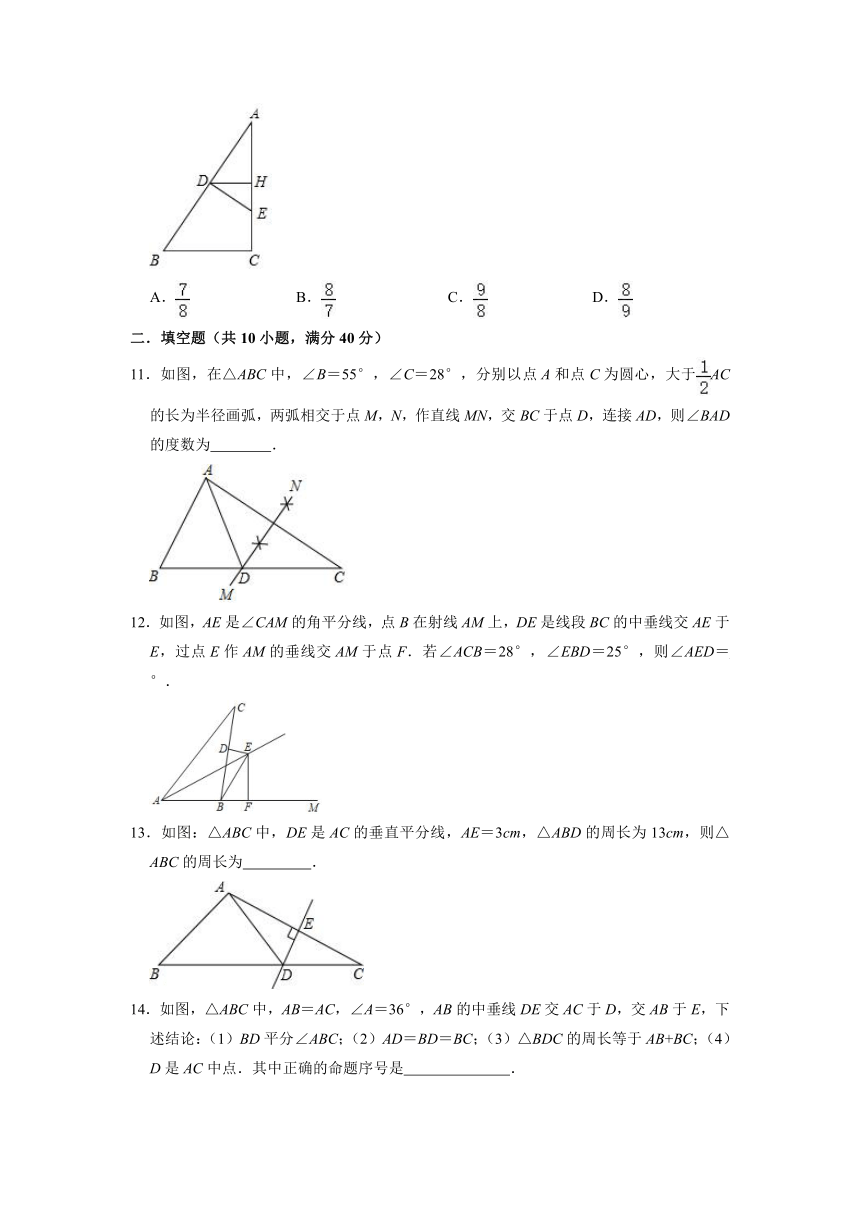
10.如图,在Rt△ABC中,∠C=90°,直线DE垂直平分AB,交AB于点D,交AC于点E,过点D作DH⊥AC于点H,已知BC=3,AC=4,则EH的长为( )
A. B. C. D.
二.填空题(共10小题,满分40分)
11.如图,在△ABC中,∠B=55°,∠C=28°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为 .
12.如图,AE是∠CAM的角平分线,点B在射线AM上,DE是线段BC的中垂线交AE于E,过点E作AM的垂线交AM于点F.若∠ACB=28°,∠EBD=25°,则∠AED= °.
13.如图:△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,则△ABC的周长为 .
14.如图,△ABC中,AB=AC,∠A=36°,AB的中垂线DE交AC于D,交AB于E,下述结论:(1)BD平分∠ABC;(2)AD=BD=BC;(3)△BDC的周长等于AB+BC;(4)D是AC中点.其中正确的命题序号是 .
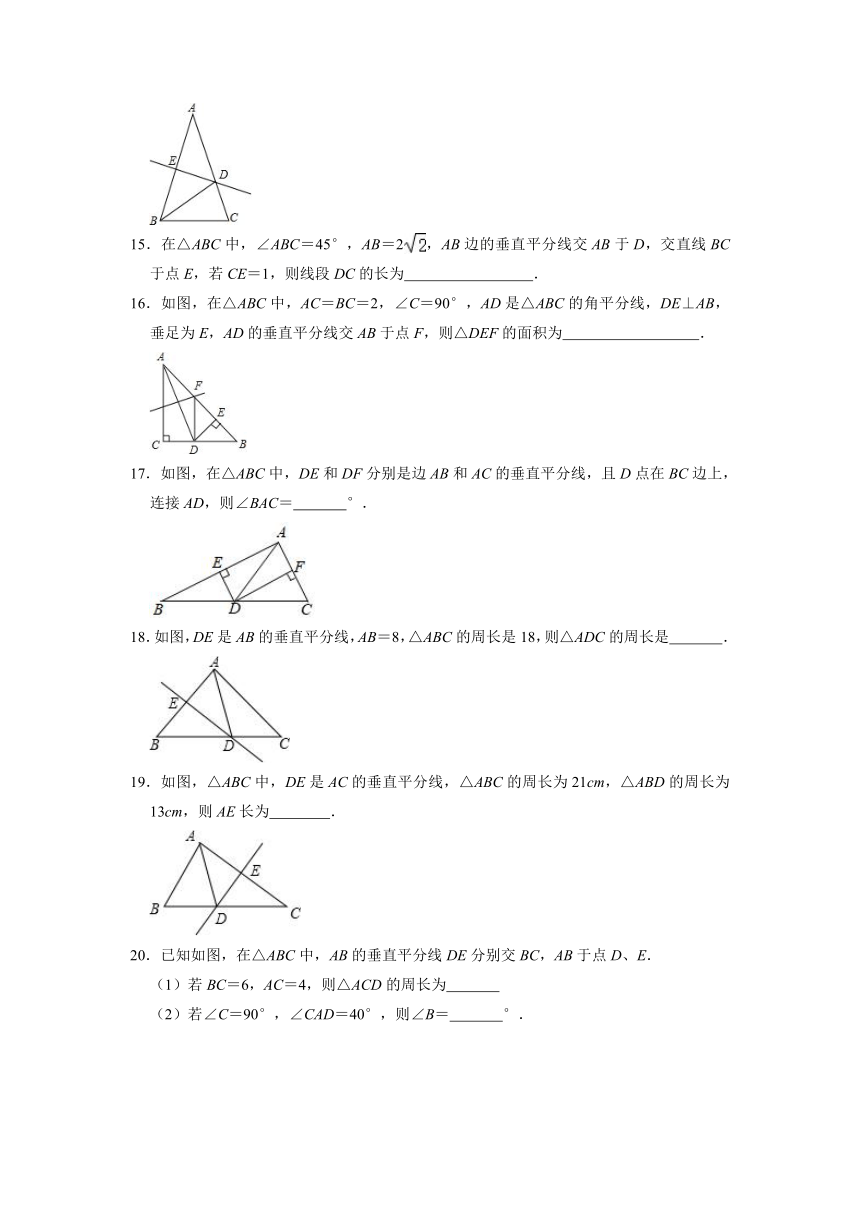
15.在△ABC中,∠ABC=45°,AB=2,AB边的垂直平分线交AB于D,交直线BC于点E,若CE=1,则线段DC的长为 .
16.如图,在△ABC中,AC=BC=2,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E,AD的垂直平分线交AB于点F,则△DEF的面积为 .
17.如图,在△ABC中,DE和DF分别是边AB和AC的垂直平分线,且D点在BC边上,连接AD,则∠BAC= °.
18.如图,DE是AB的垂直平分线,AB=8,△ABC的周长是18,则△ADC的周长是 .
19.如图,△ABC中,DE是AC的垂直平分线,△ABC的周长为21cm,△ABD的周长为13cm,则AE长为 .
20.已知如图,在△ABC中,AB的垂直平分线DE分别交BC,AB于点D、E.
(1)若BC=6,AC=4,则△ACD的周长为
(2)若∠C=90°,∠CAD=40°,则∠B= °.
三.解答题(共5小题,满分40分)
21.如图,△ABC中,AB,AC边的垂直平分线分别交BC于点D,E,垂足分别为点F,G,△ADE的周长为6cm.
(1)求△ABC中BC边的长度;
(2)若∠BAC=116°,求∠DAE的度数.
22.如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E.
(1)已知∠A=40°,求∠CBE的度数;
(2)已知△BCE的周长为8cm,AC﹣BC=2cm,求AB与BC的长.
23.如图,已知在△ABC中,AB=AC,DE、GH分别是AB、AC的垂直平分线,求证:∠BAH=∠CAE.
24.如图,已知△ABC中,AB<AC,BC边上的垂直平分线DE交BC于点D,交AC于E,若AC=9cm,△ABE的周长为16cm,求AB的长.
25.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上.
(1)线段AB,AC,CE三者之间的长度有什么关系.
(2)线段AB+BD与DE有怎样的关系呢?
参考答案
一.选择题(共10小题,满分40分)
1.解:∵DE是线段BC的垂直平分线,
∴EB=EC,
∴△ACE的周长=AE+EC+AC=AE+EB+AC=AB+AC=16,
故选:A.
2.解:∵D在直角边AB的垂直平分线上,
∴DA=DB,
∴∠DAB=∠B,
∵D在∠CAB的角平分线上,
∴∠DAB=∠DAC,
∴∠CAD=∠DAB=∠B=30°,
故选:B.
3.解:∵DE是线段AC的垂直平分线,
∴EA=EC=10,
∴∠EAC=∠C=15°,
∴∠AEB=30°,
∴AB=AE=5(cm),
故选:B.
4.解:∵∠BAC=110°,
∴∠B+∠C=180°﹣∠BAC=70°,
∵PM、QN分别是线段AB、AC的垂直平分线,
∴AP=BP,CQ=AQ,
∴∠BAP=∠B,∠CAQ=∠C,
∴∠BAP+∠CAQ=∠B+∠C=70°,
∵∠BAC=110°,
∴∠PAQ=∠BAC﹣(∠BAP+∠CAQ)=110°﹣70°=40°,
故选:A.
5.解:∵DE是线段AB的中垂线,GF是线段BC的中垂线,
∴EB=EA,GB=GC,
∵△BEG周长为16,
∴EB+GB+EG=16,
∴EA+GC+EG=16,
∴GA+EG+EG+EG+EC=16,
∴AC+2EG=16,
∵EG=1,
∴AC=14,
故选:B.
6.解:①∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
∵∠BAC=120°,
∴∠EDF=360°﹣∠AED﹣∠AFD﹣∠BAC=60°,
∴①的结论正确;
②连接AD,如图,
∵DE、DF分别是△ABC的边AB、AC边上的中垂线,
∴AD=DB,AD=DC,
∴DB=DC,
∴②的结论正确;
③∵DE⊥AB,DF⊥AC,
∴∠DMN=∠BME=90°﹣∠ABC,∠DNM=∠CNF=90°﹣∠ACB,
当AB≠AC时,∠ABC≠∠ACB,
∴∠DMN≠∠DNM,
∴DM≠DN,
∵∠MDN=60°,
∴△DMN不是等边三角形,
∴∠DMN≠∠DNM≠60°,
∴MN≠DN,
∴③的结论不正确;
④连结EF,
∵E,F分别是AB,AC的中点,
∴EF∥BC
∴∠AEF=∠ABC
又∵∠AED=∠AFD=90°,
∴∠ADF=∠AEF,
∴∠ABC=∠ADF,
∵∠FDC=∠ADF,
∴∠ABC=∠FDC,
∴④的结论正确,
故选:D.
7.解:∵DE垂直平分AB,
∴DA=DB,
∴∠DAB=∠B=35°,
∵AD是∠BAC的平分线,
∴∠DAC=∠DAB=35°,
∴∠C=180°﹣35°﹣35°﹣35°=75°,
故选:B.
8.解:∵E是BC的中点,过点E作BC的垂线交BD于点F,
∴FE垂直平分BC,
∴BF=CF,
∴∠FBC=∠FCB,
∵∠CFD=∠FBC+∠FCB=60°,
∴∠FBC=∠FCB=30°,
∵∠ACF=40°,
∴∠ACB=∠ACF+∠BCF=70°,
∵BD平分∠ABC,
∴∠ABC=2∠FBC=60°,
∴∠A=180°﹣∠ABC﹣∠ACB=50°,
故选:B.
9.解:设∠CAD=2x°,∠BAD=5x°,
∵AB的垂直平分线是DE,
∴BD=AD,
∴∠BAD=∠B,
即∠B=5x°,
∵∠C=90°,
∴∠CAB+∠B=90°,
∴2x+5x+5x=90,
解得:x=,
即∠B=∠BAD=()°,
∴∠ADC=∠B+∠BAD=()°+()°=75°,
故选:B.
10.解:如图,连接BE,
在Rt△ABC中,∠C=90°,BC=3,AC=4,
∴AB=5,
∵直线DE垂直平分AB,
∴AE=BE,AD=AB=2.5,
∵DH⊥AC,
∴DH∥BC,
∴AH=CH=AC=2,
∵∠ADE=∠C=90°,∠A=∠A,
∴AE=,
∴HE=AE﹣AH=,
故选:C.
二.填空题(共10小题,满分40分)
11.解:∵△ABC中,∠B=55°,∠C=28°,
∴∠BAC=180°﹣55°﹣28°=97°.
∵直线MN是线段AC的垂直平分线,
∴∠C=∠CAD=28°,
∴∠BAD=∠BAC﹣∠CAD=97°﹣28°=69°.
故答案为:69°.
12.解:连接CE,过E作ER⊥AC于R,CD交ER于Q,AE交BC于O,
∵DE是线段BC的中垂线,
∴∠EDC=90°,CE=BE,
∴∠ECB=∠EBD,
∵∠EBD=25°,
∴∠ECB=25°,
∴∠DEB=∠CED=90°﹣25°=65°,
∵ER⊥AC,ED⊥BC,
∴∠QRC=∠QDE=90°,
∴∠ACB+∠CQR=90°,∠EQD+∠QED=90°,
∵∠CQR=∠EQD,
∴∠ACB=∠QED,
∵∠ACB=28°,
∴∠QED=28°,
∵AE平分∠CAM,ER⊥AC,EF⊥AM,
∴ER=EF,
在Rt△ERC和Rt△EFB中,
,
∴Rt△ERC≌Rt△EFB(HL),
∴∠EBF=∠ACE=∠ACB+∠ECD=28°+25°=53°,
∵∠EFB=90°,
∴∠BEF=90°﹣∠EBF=90°﹣53°=37°,
∴∠REF=∠RED+∠BED+∠BEF=28°+65°+37°=130°,
∵∠ARE=∠AFE=90°,
∴∠CAM=360°﹣90°﹣90°﹣130°=50°,
∵AE平分∠CAM,
∴∠CAE=CAM=25°,
∴∠DOE=∠CAE+∠ACB=25°+28°=53°,
∵ED⊥BC,
∴∠EDB=90°,
∴∠AED=90°﹣∠DOE=90°﹣53°=37°,
故答案为:37.
13.解:∵DE是AC的垂直平分线,
∴AD=CD,AC=2AE=6cm,
又∵△ABD的周长=AB+BD+AD=13cm,
∴AB+BD+CD=13cm,
即AB+BC=13cm,
∴△ABC的周长=AB+BC+AC=13+6=19cm.
故答案为19cm.
14.解:∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵DE是AB的垂直平分线,
∴AD=BD,∠ABD=∠A=36°,
∴∠DBC=72°﹣36°=36°,
∠BDC=180°﹣36°﹣72°=72°,
∴BD=BC;
(1)BD平分∠ABC正确;
(2)AD=BD=BC正确;
(3)△BDC的周长=BC+CD+BD
=BC+CD+AD
=BC+AC
=AB+BC,正确;
(4)AD=BD≠CD,所以D不是AC的中点,故本选项错误.
故正确的命题是(1)(2)(3).
15.解:当E点在线段BC上时,
如图,过点D作DF⊥BC,垂足为F,
∵线段AB的垂直平分线交直线BC于点E,
∴AE=BE,
∴∠BAE=∠ABC=45°,
∴∠AEB=90°,
∵∠ABC=45°,∠BDE=90°,
∴∠BED=45°,
∴BD=ED,
∵AB=2,
∴BD=DE=,
∴BE==2,
∵BD=DE,DF⊥BE,
∴EF=BE=1,
∴DF=EF=1,
∵CE=1,
∴CF=2,
在Rt△CDF中,根据勾股定理得:
CD==;
当点E在BC的延长线上时,
如图,∵线段AB的垂直平分线交直线BC于点E,
∵∠ABC=45°,AB=2 ,
由(1)同理可得:BE=2,
∵CE=1,
∴BC=1,
如图,过点C作CF⊥AB,垂足为F,
∴BF=CF==,
∴DF=,
在Rt△CDF中,由勾股定理得:
CD=,
综上:CD=1或,
故答案为:1或.
16.解:∵AD是△ABC的角平分线,∠ACB=90°,DE⊥AB,
∴∠CAD=∠EAD,DE=CD,AE=AC=2,
∵AD的垂直平分线交AB于点F,
∴AF=DF,
∴∠ADF=∠EAD,
∴∠ADF=∠CAD,
∴AC∥DE,
∴∠BDE=∠C=90°,
∴△BDF、△BED是等腰直角三角形,
设DE=x,则EF=BE=x,BD=DF=2﹣x,
在Rt△BED中,DE2+BE2=BD2,
∴x2+x2=(2﹣x)2,
解得x1=﹣2﹣2(负值舍去),x2=﹣2+2,
∴△DEF的面积为(﹣2+2)×(﹣2+2)÷2=6﹣4.
故答案为:6﹣4.
17.解:∵DE和DF分别是边AB和AC的垂直平分线,
∴BD=AD,AD=CD,
∴∠B=∠BAD,∠C=∠CAD,
∵∠B+∠C+BAC=180°,
∴2∠BAD+2∠CAD=180°,
∴∠BAD+∠CAD=90°,
即∠BAC=90°,
故答案为:90.
18.解:∵DE是AB的垂直平分线,
∴AD=BD.
∴△ADC的周长=AD+DC+AC=BD+DC+AC=BC+AC=18﹣8=10.
故答案为:10.
19.解:∵DE是AC的垂直平分线,
∴AD=DC,AE=CE=AC,
∵△ABC的周长为21cm,△ABD的周长为13cm,
∴AB+BC+AC=21cm,AB+BD+AD=AB+BD+DC=AB+BC=13cm,
∴AC=8cm,
∴AE=4cm,
故答案为:4cm
20.解:(1)∵AB的垂直平分线DE分别交BC,AB于点D、E,
∴BD=AD,
∵AC=4,BC=6,
∴△ACD的周长为AC+AD+CD=AC+BD+CD=AC+BC=4+6=10,
故答案为:10;
(2)∵∠C=90°,∠CAD=40°,
∴∠ADC=180°﹣∠C﹣∠CAD=50°,
∴∠B+∠BAD=∠ADC=50°,
∵AD=BD,
∴∠B=∠BAD,
∴∠B=50°=25°,
故答案为:25.
三.解答题(共5小题,满分40分)
21.解:(1)∵AB的中垂线交BC于D,AC的中垂线交BC于E,
∴DA=DB,EA=EC,
则△ADE的周长=AD+DE+AE=BD+DE+EC=BC=6(cm),
∴BC=6cm,
(2)∵∠BAC=116°,
∴∠B+∠C=180°﹣116°=64°,
∵DA=DB,EA=EC,
∴∠B=∠DAB,∠C=∠EAC,
∵∠ADE=∠B+∠DAB,∠AED=∠C+∠EAC,
∴∠ADE+∠AED=128°,
∴∠DAE=180°﹣128°=52°.
22.解:(1)∵AB=AC,∠A=40°,
∴∠ABC=70°
∵DE垂直平分AB,
∴AE=BE,
∴∠ABE=∠A=40°,
∴∠CBE=∠ABC﹣∠EBA
=70°﹣40°=30°.
(2)∵△BCE的周长为8cm,
∴BE+EC+BC=8cm.
∵AE=BE,
∴AE+EC+BC=8cm,
即AC+BC=8cm.
∵AC﹣BC=2cm,
∴AC=5cm,BC=3cm.
∵AB=AC,
∴AB=5cm.
23.证明:∵△ABC中,AB=AC,
∴∠B=∠C,
∵DE、GH分别是AB、AC的垂直平分线,
∴∠B=∠BAE=∠C=∠CAH,
∴∠BAE+∠EAH=∠CAH+∠EAH,
即∠BAH=∠CAE.
24.解:∵ED是线段BC的垂直平分线,
∴BE=CE,
∴BE+AE=CE+AE=AC=9cm,
∵△ABE的周长为16cm,
∴AB=16﹣(BE+AE)=16﹣9=7cm.
25.解:(1)AB=AC=CE,
∵AD⊥BC,BD=DC,
∴AB=AC;
又∵点C在AE的垂直平分线上,
∴AC=EC,
∴AB=AC=CE;
(2)AB+BD=DE,
理由是:∵AB=AC=CE,
∵AC+CD=AB+BD,
∴DE=EC+CD=AB+BD,
即AB+BD=EC+CD=DE.
一.选择题(共10小题,满分40分)
1.如图,△ABC中,AB=10,边BC的垂直平分线DE分别交AB、BC于E、D,且AC=6,则△ACE的周长为( )
A.16 B.18 C.22 D.26
2.在Rt△ABC中,∠C=90°,有一点D同时满足以下三个条件:①在直角边BC上;②在∠CAB的角平分线上;③在斜边AB的垂直平分线上,那么∠B为( )
A.15° B.30° C.45° D.60°
3.如图,∠ABC=90°,∠C=15°,线段AC的垂直平分线DE交AC于D,交BC于E,D为垂足,CE=10 cm,则AB=( )
A.4 cm B.5 cm C.6 cm D.不能确定
4.如图,在△ABC中,PM、QN分别是线段AB、AC的垂直平分线,若∠BAC=110°,则∠PAQ的度数是( )
A.40° B.50° C.60° D.70°
5.如图,在△ABC中,AB边的中垂线DE,分别与AB、AC边交于点D、E两点,BC边的中垂线FG,分别与BC、AC边交于点F、G两点,连接BE、BG.若△BEG的周长为16,GE=1.则AC的长为( )
A.13 B.14 C.15 D.16
6.如图,在△ABC中,∠A=120°,AB、AC边上的中垂线DE、DF交于点D,垂足分别为点E、F,DE、DF分别交BC于点M、N,连接BD,CD.下列结论:①∠EDF=60°;②DB=DC;③MN=DN;④∠ABC=∠FDC.其中正确的结论是( )
A.①③④ B.①②③ C.②③④ D.①②④
7.如图,△ABC中,∠B=35°,∠BAC的平分线AD交BC于点D,若DE垂直平分AB,则∠C的度数为( )
A.80° B.75° C.65° D.60°
8.如图,△ABC中,BD平分∠ABC,E是BC的中点,过点E作BC的垂线交BD于点F,连接CF,若∠DFC=60°,∠ACF=40°,则∠A的度数为( )
A.45° B.50° C.55° D.60°
9.如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点D,交AB于点E,连接AD,AD将∠CAB分成两个角,且∠CAD:∠BAD=2:5,则∠ADC的度数是( )
A.70° B.75° C.80° D.85°
10.如图,在Rt△ABC中,∠C=90°,直线DE垂直平分AB,交AB于点D,交AC于点E,过点D作DH⊥AC于点H,已知BC=3,AC=4,则EH的长为( )
A. B. C. D.
二.填空题(共10小题,满分40分)
11.如图,在△ABC中,∠B=55°,∠C=28°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为 .
12.如图,AE是∠CAM的角平分线,点B在射线AM上,DE是线段BC的中垂线交AE于E,过点E作AM的垂线交AM于点F.若∠ACB=28°,∠EBD=25°,则∠AED= °.
13.如图:△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,则△ABC的周长为 .
14.如图,△ABC中,AB=AC,∠A=36°,AB的中垂线DE交AC于D,交AB于E,下述结论:(1)BD平分∠ABC;(2)AD=BD=BC;(3)△BDC的周长等于AB+BC;(4)D是AC中点.其中正确的命题序号是 .
15.在△ABC中,∠ABC=45°,AB=2,AB边的垂直平分线交AB于D,交直线BC于点E,若CE=1,则线段DC的长为 .
16.如图,在△ABC中,AC=BC=2,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E,AD的垂直平分线交AB于点F,则△DEF的面积为 .
17.如图,在△ABC中,DE和DF分别是边AB和AC的垂直平分线,且D点在BC边上,连接AD,则∠BAC= °.
18.如图,DE是AB的垂直平分线,AB=8,△ABC的周长是18,则△ADC的周长是 .
19.如图,△ABC中,DE是AC的垂直平分线,△ABC的周长为21cm,△ABD的周长为13cm,则AE长为 .
20.已知如图,在△ABC中,AB的垂直平分线DE分别交BC,AB于点D、E.
(1)若BC=6,AC=4,则△ACD的周长为
(2)若∠C=90°,∠CAD=40°,则∠B= °.
三.解答题(共5小题,满分40分)
21.如图,△ABC中,AB,AC边的垂直平分线分别交BC于点D,E,垂足分别为点F,G,△ADE的周长为6cm.
(1)求△ABC中BC边的长度;
(2)若∠BAC=116°,求∠DAE的度数.
22.如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E.
(1)已知∠A=40°,求∠CBE的度数;
(2)已知△BCE的周长为8cm,AC﹣BC=2cm,求AB与BC的长.
23.如图,已知在△ABC中,AB=AC,DE、GH分别是AB、AC的垂直平分线,求证:∠BAH=∠CAE.
24.如图,已知△ABC中,AB<AC,BC边上的垂直平分线DE交BC于点D,交AC于E,若AC=9cm,△ABE的周长为16cm,求AB的长.
25.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上.
(1)线段AB,AC,CE三者之间的长度有什么关系.
(2)线段AB+BD与DE有怎样的关系呢?
参考答案
一.选择题(共10小题,满分40分)
1.解:∵DE是线段BC的垂直平分线,
∴EB=EC,
∴△ACE的周长=AE+EC+AC=AE+EB+AC=AB+AC=16,
故选:A.
2.解:∵D在直角边AB的垂直平分线上,
∴DA=DB,
∴∠DAB=∠B,
∵D在∠CAB的角平分线上,
∴∠DAB=∠DAC,
∴∠CAD=∠DAB=∠B=30°,
故选:B.
3.解:∵DE是线段AC的垂直平分线,
∴EA=EC=10,
∴∠EAC=∠C=15°,
∴∠AEB=30°,
∴AB=AE=5(cm),
故选:B.
4.解:∵∠BAC=110°,
∴∠B+∠C=180°﹣∠BAC=70°,
∵PM、QN分别是线段AB、AC的垂直平分线,
∴AP=BP,CQ=AQ,
∴∠BAP=∠B,∠CAQ=∠C,
∴∠BAP+∠CAQ=∠B+∠C=70°,
∵∠BAC=110°,
∴∠PAQ=∠BAC﹣(∠BAP+∠CAQ)=110°﹣70°=40°,
故选:A.
5.解:∵DE是线段AB的中垂线,GF是线段BC的中垂线,
∴EB=EA,GB=GC,
∵△BEG周长为16,
∴EB+GB+EG=16,
∴EA+GC+EG=16,
∴GA+EG+EG+EG+EC=16,
∴AC+2EG=16,
∵EG=1,
∴AC=14,
故选:B.
6.解:①∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
∵∠BAC=120°,
∴∠EDF=360°﹣∠AED﹣∠AFD﹣∠BAC=60°,
∴①的结论正确;
②连接AD,如图,
∵DE、DF分别是△ABC的边AB、AC边上的中垂线,
∴AD=DB,AD=DC,
∴DB=DC,
∴②的结论正确;
③∵DE⊥AB,DF⊥AC,
∴∠DMN=∠BME=90°﹣∠ABC,∠DNM=∠CNF=90°﹣∠ACB,
当AB≠AC时,∠ABC≠∠ACB,
∴∠DMN≠∠DNM,
∴DM≠DN,
∵∠MDN=60°,
∴△DMN不是等边三角形,
∴∠DMN≠∠DNM≠60°,
∴MN≠DN,
∴③的结论不正确;
④连结EF,
∵E,F分别是AB,AC的中点,
∴EF∥BC
∴∠AEF=∠ABC
又∵∠AED=∠AFD=90°,
∴∠ADF=∠AEF,
∴∠ABC=∠ADF,
∵∠FDC=∠ADF,
∴∠ABC=∠FDC,
∴④的结论正确,
故选:D.
7.解:∵DE垂直平分AB,
∴DA=DB,
∴∠DAB=∠B=35°,
∵AD是∠BAC的平分线,
∴∠DAC=∠DAB=35°,
∴∠C=180°﹣35°﹣35°﹣35°=75°,
故选:B.
8.解:∵E是BC的中点,过点E作BC的垂线交BD于点F,
∴FE垂直平分BC,
∴BF=CF,
∴∠FBC=∠FCB,
∵∠CFD=∠FBC+∠FCB=60°,
∴∠FBC=∠FCB=30°,
∵∠ACF=40°,
∴∠ACB=∠ACF+∠BCF=70°,
∵BD平分∠ABC,
∴∠ABC=2∠FBC=60°,
∴∠A=180°﹣∠ABC﹣∠ACB=50°,
故选:B.
9.解:设∠CAD=2x°,∠BAD=5x°,
∵AB的垂直平分线是DE,
∴BD=AD,
∴∠BAD=∠B,
即∠B=5x°,
∵∠C=90°,
∴∠CAB+∠B=90°,
∴2x+5x+5x=90,
解得:x=,
即∠B=∠BAD=()°,
∴∠ADC=∠B+∠BAD=()°+()°=75°,
故选:B.
10.解:如图,连接BE,
在Rt△ABC中,∠C=90°,BC=3,AC=4,
∴AB=5,
∵直线DE垂直平分AB,
∴AE=BE,AD=AB=2.5,
∵DH⊥AC,
∴DH∥BC,
∴AH=CH=AC=2,
∵∠ADE=∠C=90°,∠A=∠A,
∴AE=,
∴HE=AE﹣AH=,
故选:C.
二.填空题(共10小题,满分40分)
11.解:∵△ABC中,∠B=55°,∠C=28°,
∴∠BAC=180°﹣55°﹣28°=97°.
∵直线MN是线段AC的垂直平分线,
∴∠C=∠CAD=28°,
∴∠BAD=∠BAC﹣∠CAD=97°﹣28°=69°.
故答案为:69°.
12.解:连接CE,过E作ER⊥AC于R,CD交ER于Q,AE交BC于O,
∵DE是线段BC的中垂线,
∴∠EDC=90°,CE=BE,
∴∠ECB=∠EBD,
∵∠EBD=25°,
∴∠ECB=25°,
∴∠DEB=∠CED=90°﹣25°=65°,
∵ER⊥AC,ED⊥BC,
∴∠QRC=∠QDE=90°,
∴∠ACB+∠CQR=90°,∠EQD+∠QED=90°,
∵∠CQR=∠EQD,
∴∠ACB=∠QED,
∵∠ACB=28°,
∴∠QED=28°,
∵AE平分∠CAM,ER⊥AC,EF⊥AM,
∴ER=EF,
在Rt△ERC和Rt△EFB中,
,
∴Rt△ERC≌Rt△EFB(HL),
∴∠EBF=∠ACE=∠ACB+∠ECD=28°+25°=53°,
∵∠EFB=90°,
∴∠BEF=90°﹣∠EBF=90°﹣53°=37°,
∴∠REF=∠RED+∠BED+∠BEF=28°+65°+37°=130°,
∵∠ARE=∠AFE=90°,
∴∠CAM=360°﹣90°﹣90°﹣130°=50°,
∵AE平分∠CAM,
∴∠CAE=CAM=25°,
∴∠DOE=∠CAE+∠ACB=25°+28°=53°,
∵ED⊥BC,
∴∠EDB=90°,
∴∠AED=90°﹣∠DOE=90°﹣53°=37°,
故答案为:37.
13.解:∵DE是AC的垂直平分线,
∴AD=CD,AC=2AE=6cm,
又∵△ABD的周长=AB+BD+AD=13cm,
∴AB+BD+CD=13cm,
即AB+BC=13cm,
∴△ABC的周长=AB+BC+AC=13+6=19cm.
故答案为19cm.
14.解:∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵DE是AB的垂直平分线,
∴AD=BD,∠ABD=∠A=36°,
∴∠DBC=72°﹣36°=36°,
∠BDC=180°﹣36°﹣72°=72°,
∴BD=BC;
(1)BD平分∠ABC正确;
(2)AD=BD=BC正确;
(3)△BDC的周长=BC+CD+BD
=BC+CD+AD
=BC+AC
=AB+BC,正确;
(4)AD=BD≠CD,所以D不是AC的中点,故本选项错误.
故正确的命题是(1)(2)(3).
15.解:当E点在线段BC上时,
如图,过点D作DF⊥BC,垂足为F,
∵线段AB的垂直平分线交直线BC于点E,
∴AE=BE,
∴∠BAE=∠ABC=45°,
∴∠AEB=90°,
∵∠ABC=45°,∠BDE=90°,
∴∠BED=45°,
∴BD=ED,
∵AB=2,
∴BD=DE=,
∴BE==2,
∵BD=DE,DF⊥BE,
∴EF=BE=1,
∴DF=EF=1,
∵CE=1,
∴CF=2,
在Rt△CDF中,根据勾股定理得:
CD==;
当点E在BC的延长线上时,
如图,∵线段AB的垂直平分线交直线BC于点E,
∵∠ABC=45°,AB=2 ,
由(1)同理可得:BE=2,
∵CE=1,
∴BC=1,
如图,过点C作CF⊥AB,垂足为F,
∴BF=CF==,
∴DF=,
在Rt△CDF中,由勾股定理得:
CD=,
综上:CD=1或,
故答案为:1或.
16.解:∵AD是△ABC的角平分线,∠ACB=90°,DE⊥AB,
∴∠CAD=∠EAD,DE=CD,AE=AC=2,
∵AD的垂直平分线交AB于点F,
∴AF=DF,
∴∠ADF=∠EAD,
∴∠ADF=∠CAD,
∴AC∥DE,
∴∠BDE=∠C=90°,
∴△BDF、△BED是等腰直角三角形,
设DE=x,则EF=BE=x,BD=DF=2﹣x,
在Rt△BED中,DE2+BE2=BD2,
∴x2+x2=(2﹣x)2,
解得x1=﹣2﹣2(负值舍去),x2=﹣2+2,
∴△DEF的面积为(﹣2+2)×(﹣2+2)÷2=6﹣4.
故答案为:6﹣4.
17.解:∵DE和DF分别是边AB和AC的垂直平分线,
∴BD=AD,AD=CD,
∴∠B=∠BAD,∠C=∠CAD,
∵∠B+∠C+BAC=180°,
∴2∠BAD+2∠CAD=180°,
∴∠BAD+∠CAD=90°,
即∠BAC=90°,
故答案为:90.
18.解:∵DE是AB的垂直平分线,
∴AD=BD.
∴△ADC的周长=AD+DC+AC=BD+DC+AC=BC+AC=18﹣8=10.
故答案为:10.
19.解:∵DE是AC的垂直平分线,
∴AD=DC,AE=CE=AC,
∵△ABC的周长为21cm,△ABD的周长为13cm,
∴AB+BC+AC=21cm,AB+BD+AD=AB+BD+DC=AB+BC=13cm,
∴AC=8cm,
∴AE=4cm,
故答案为:4cm
20.解:(1)∵AB的垂直平分线DE分别交BC,AB于点D、E,
∴BD=AD,
∵AC=4,BC=6,
∴△ACD的周长为AC+AD+CD=AC+BD+CD=AC+BC=4+6=10,
故答案为:10;
(2)∵∠C=90°,∠CAD=40°,
∴∠ADC=180°﹣∠C﹣∠CAD=50°,
∴∠B+∠BAD=∠ADC=50°,
∵AD=BD,
∴∠B=∠BAD,
∴∠B=50°=25°,
故答案为:25.
三.解答题(共5小题,满分40分)
21.解:(1)∵AB的中垂线交BC于D,AC的中垂线交BC于E,
∴DA=DB,EA=EC,
则△ADE的周长=AD+DE+AE=BD+DE+EC=BC=6(cm),
∴BC=6cm,
(2)∵∠BAC=116°,
∴∠B+∠C=180°﹣116°=64°,
∵DA=DB,EA=EC,
∴∠B=∠DAB,∠C=∠EAC,
∵∠ADE=∠B+∠DAB,∠AED=∠C+∠EAC,
∴∠ADE+∠AED=128°,
∴∠DAE=180°﹣128°=52°.
22.解:(1)∵AB=AC,∠A=40°,
∴∠ABC=70°
∵DE垂直平分AB,
∴AE=BE,
∴∠ABE=∠A=40°,
∴∠CBE=∠ABC﹣∠EBA
=70°﹣40°=30°.
(2)∵△BCE的周长为8cm,
∴BE+EC+BC=8cm.
∵AE=BE,
∴AE+EC+BC=8cm,
即AC+BC=8cm.
∵AC﹣BC=2cm,
∴AC=5cm,BC=3cm.
∵AB=AC,
∴AB=5cm.
23.证明:∵△ABC中,AB=AC,
∴∠B=∠C,
∵DE、GH分别是AB、AC的垂直平分线,
∴∠B=∠BAE=∠C=∠CAH,
∴∠BAE+∠EAH=∠CAH+∠EAH,
即∠BAH=∠CAE.
24.解:∵ED是线段BC的垂直平分线,
∴BE=CE,
∴BE+AE=CE+AE=AC=9cm,
∵△ABE的周长为16cm,
∴AB=16﹣(BE+AE)=16﹣9=7cm.
25.解:(1)AB=AC=CE,
∵AD⊥BC,BD=DC,
∴AB=AC;
又∵点C在AE的垂直平分线上,
∴AC=EC,
∴AB=AC=CE;
(2)AB+BD=DE,
理由是:∵AB=AC=CE,
∵AC+CD=AB+BD,
∴DE=EC+CD=AB+BD,
即AB+BD=EC+CD=DE.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
