2021-2022学年冀教版八年级数学上册16.2线段的垂直平分线 优生辅导训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年冀教版八年级数学上册16.2线段的垂直平分线 优生辅导训练(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 390.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 10:09:11 | ||
图片预览




文档简介
2021-2022学年冀教版八年级数学上册《16.2线段的垂直平分线》优生辅导训练(附答案)
1.到三角形三个顶点距离都相等的点是( )
A.三角形的三条角平分线的交点 B.三角形的三边垂直平分线的交点
C.三角形的三条高线的交点 D.三角形的三条中线的交点
2.如图,△ABC中,DE是AC的垂直平分线,△ABC的周长为21cm,△ABD的周长为13cm,则AE长为( )
A.8cm B.6cm C.4cm D.10cm
3.如图,在△ABC中,BC边的中垂线DE,分别与AB、BC边交于点D、E两点,连接CD,边AC的中垂线FG分别与CD、AC边交于点F、G两点,连接AF.若△ADF的周长为13,AD=4,则BD的长为( )
A.4 B.9 C.13 D.17
4.如图,在△ABC中,直线l为边BC的垂直平分线,l交AC于点Q,∠ABC的角平分线与l相交于点P.若∠BAC=60°,∠ACP=24°,则∠PQC是( )
A.34° B.36° C.44° D.46°
5.如图,直线l,m相交于点O.P为这两直线外一点,且OP=2.8.若点P关于直线l,m的对称点分别是点P1,P2,则P1,P2之间的距离可能是( )
A.0 B.5 C.6 D.7
6.如图,电信部门要在公路l旁修建一座移动信号发射塔.按照设计要求,发射塔到两个城镇M,N的距离必须相等,则发射塔应该建在( )
A.A处 B.B处 C.C处 D.D处
7.如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )
A.1对 B.2对 C.3对 D.4对
8.已知:如图,∠AOB内一点P,P1,P2分别P是关于OA、OB的对称点,P1P2交OA于M,交OB于N,若P1P2=5cm,则△PMN的周长是( )
A.3cm B.4cm C.5cm D.6cm
9.如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.若△ABC的周长为26cm,AC=10cm,则DC的长为( )
A.10cm B.9cm C.8cm D.7cm
10.如图,在△ABC中,AD⊥BC于点D,BD=DC,若BC=6,AD=7,则图中阴影部分图形的面积为 .
11.如图,在△ABC中,∠C=90°,∠B=22.5°,DE垂直平分AB交BC于点E,EC=2,则△ACE的面积为 .
12.如图,△ABC中,AB+AC=4,BC的垂直平分线l交AC于D,则△ABD的周长为 .
13.如图,△ABC中,ED垂直平分AB,交AB于点D,交AC于点F,交BC的延长线于点E,若BF=6,CF=2,则AC的长为 .
14.如图,在△ABC中,AC的垂直平分线分别交BC、AC于点D、G,AB的垂直平分线分别交BC、AB于点E、F,连接AD、AE,若C△ADE=13,DE=2,则BC= .
15.如图,在△ABC中,∠BAC=120°,分别作AC,AB两边的垂直平分线PM、PN,垂足分别是点M、N,以下说法:①∠P=60°;②∠EAF=∠B+∠C;③PE=PF;④点P到点B和点C的距离相等.其中正确的是 (填序号).
16.如图,A、B表示两个仓库,要在A、B一侧的河岸边建造一个码头,使它到两个仓库的距离相等,码头应建造在什么位置?
17.如图,在△ABC中,DE是AC的垂直平分线.
(1)若AC=6,△ABD的周长是13,则△ABC的周长是 ;
(2)若△ABC中,∠B=62°,∠C=36°,求∠BAD的度数.
18.如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接OB,OC.若△ADE的周长为12cm,△OBC的周长为32cm.
(1)求线段BC的长;
(2)连接OA,求线段OA的长;
(3)若∠BAC=n°(n>90),直接写出∠DAE的度数 °.
19.已知:△ABC是三边都不相等的三角形,点O和点P是这个三角形内部两点.
(1)如图①,如果点P是这个三角形三个内角平分线的交点,那么∠BPC和∠BAC有怎样的数量关系?请说明理由;
(2)如图②,如果点O是这个三角形三边垂直平分线的交点,那么∠BOC和∠BAC有怎样的数量关系?请说明理由;
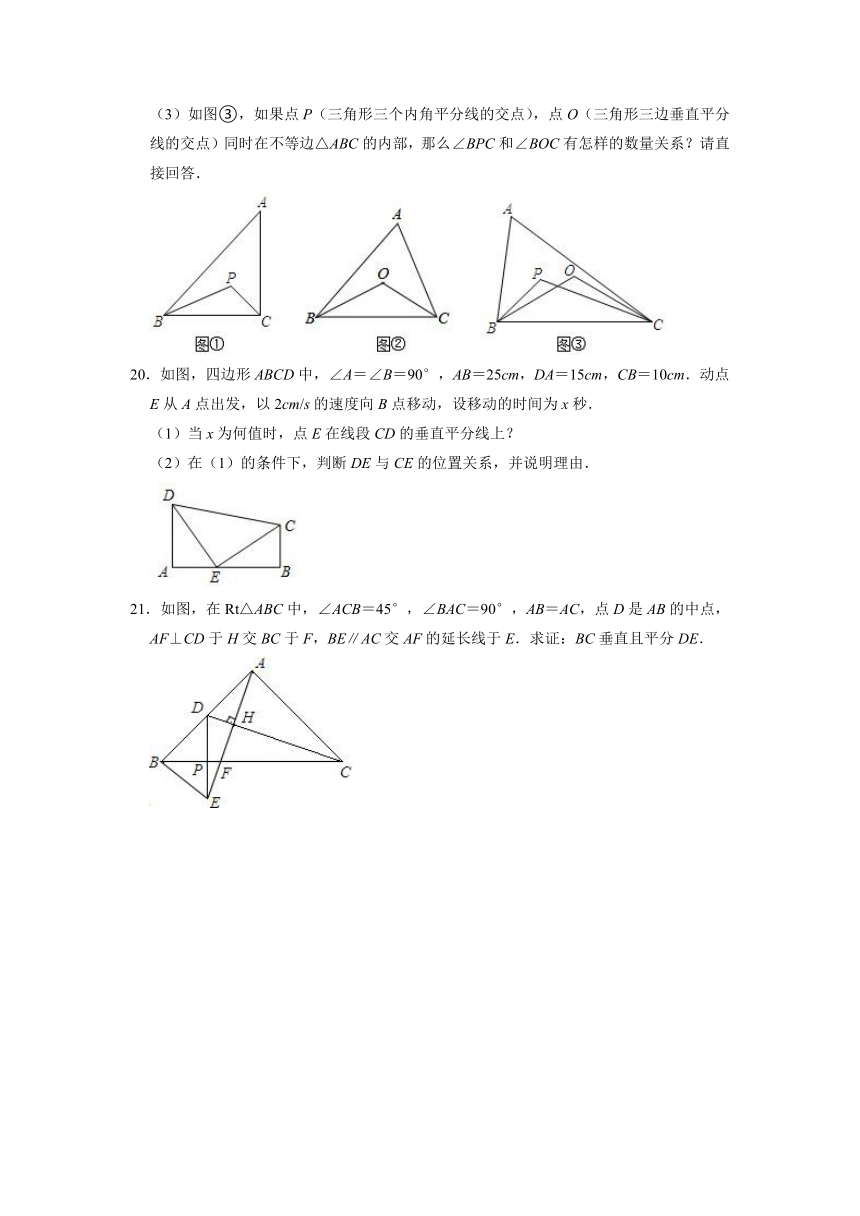
(3)如图③,如果点P(三角形三个内角平分线的交点),点O(三角形三边垂直平分线的交点)同时在不等边△ABC的内部,那么∠BPC和∠BOC有怎样的数量关系?请直接回答.
20.如图,四边形ABCD中,∠A=∠B=90°,AB=25cm,DA=15cm,CB=10cm.动点
E从A点出发,以2cm/s的速度向B点移动,设移动的时间为x秒.
(1)当x为何值时,点E在线段CD的垂直平分线上?
(2)在(1)的条件下,判断DE与CE的位置关系,并说明理由.
21.如图,在Rt△ABC中,∠ACB=45°,∠BAC=90°,AB=AC,点D是AB的中点,AF⊥CD于H交BC于F,BE∥AC交AF的延长线于E.求证:BC垂直且平分DE.
参考答案
1.到三角形三个顶点距离都相等的点是( )
A.三角形的三条角平分线的交点
B.三角形的三边垂直平分线的交点
C.三角形的三条高线的交点
D.三角形的三条中线的交点
解:∵到三角形的一边的两端点距离相等的点在这边的垂直平分线上,
∴到三角形三个顶点的距离都相等的点是这个三角形的三条边的垂直平分线的交点,
故选:B.
2.如图,△ABC中,DE是AC的垂直平分线,△ABC的周长为21cm,△ABD的周长为13cm,则AE长为( )
A.8cm B.6cm C.4cm D.10cm
解:∵DE是AC的垂直平分线,
∴DA=DC,AE=EC,
∵△ABC的周长为21cm,
∴AB+BC+AC=21cm,
∵△ABD的周长为13cm,
∴AB+BD+AD=AB+BD+DC=AB+BC=13cm,
∴AC=8cm,
∴AE=4cm,
故选:C.
3.如图,在△ABC中,BC边的中垂线DE,分别与AB、BC边交于点D、E两点,连接CD,边AC的中垂线FG分别与CD、AC边交于点F、G两点,连接AF.若△ADF的周长为13,AD=4,则BD的长为( )
A.4 B.9 C.13 D.17
解:∵边AC的中垂线FG分别与CD、AC边交于点F、G两点,连接AF.
∴CF=AF,
∴△ADF的周长=AF+DF+AD=CF+DF+AD=CD+AD=13,
∵AD=4,
∴CD=9,
∵DE是BC边的中垂线,
∴BD=CD=9,
故选:B.
4.如图,在△ABC中,直线l为边BC的垂直平分线,l交AC于点Q,∠ABC的角平分线与l相交于点P.若∠BAC=60°,∠ACP=24°,则∠PQC是( )
A.34° B.36° C.44° D.46°
解:∵BP平分∠ABC,
∴∠ABP=∠CBP,
∵直线l是线段BC的垂直平分线,
∴BP=CP,
∴∠CBP=∠BCP,
∴∠ABP=∠BCP,
∵∠A+∠ACB+∠ABC=180°,∠A=60°,∠ACP=24°,
∴3∠ABP+24°+60°=180°,
∴∠ABP=32°,
∴∠PBC=∠PCB=32°,
∴∠PQC=×(180°﹣32°﹣32°)﹣24°=58°﹣24°=34°,
故选:A.
5.如图,直线l,m相交于点O.P为这两直线外一点,且OP=2.8.若点P关于直线l,m的对称点分别是点P1,P2,则P1,P2之间的距离可能是( )
A.0 B.5 C.6 D.7
解:连接OP1,OP2,P1P2,
∵点P关于直线l,m的对称点分别是点P1,P2,
∴OP1=OP=2.8,OP=OP2=2.8,
OP1+OP2>P1P2,
0<P1P2<5.6,
故选:B.
6.如图,电信部门要在公路l旁修建一座移动信号发射塔.按照设计要求,发射塔到两个城镇M,N的距离必须相等,则发射塔应该建在( )
A.A处 B.B处 C.C处 D.D处
解:
根据作图可知:EF是线段MN的垂直平分线,
所以EF上的点到M、N的距离相等,
即发射塔应该建在C处,
故选:C.
7.如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )
A.1对 B.2对 C.3对 D.4对
解:∵EF是AC的垂直平分线,
∴OA=OC,
又∵OE=OE,
∴Rt△AOE≌Rt△COE,
∵AB=AC,D是BC的中点,
∴AD⊥BC,
∴△ABC关于直线AD轴对称,
∴△AOC≌△AOB,△BOD≌△COD,△ABD≌△ACD,
综上所述,全等三角形共有4对.
故选:D.
8.已知:如图,∠AOB内一点P,P1,P2分别P是关于OA、OB的对称点,P1P2交OA于M,交OB于N,若P1P2=5cm,则△PMN的周长是( )
A.3cm B.4cm C.5cm D.6cm
解:∵P与P1关于OA对称,
∴OA为线段PP1的垂直平分线,
∴MP=MP1,
同理,P与P2关于OB对称,
∴OB为线段PP2的垂直平分线,
∴NP=NP2,
∴P1P2=P1M+MN+NP2=MP+MN+NP=5cm,
则△PMN的周长为5cm.
故选:C.
9.如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.若△ABC的周长为26cm,AC=10cm,则DC的长为( )
A.10cm B.9cm C.8cm D.7cm
解:∵△ABC的周长为26cm,AC=10cm,
∴AB+BC=16cm,
∴AB+BE+EC=16cm,
即2DE+2EC=16cm,
∴DE+EC=8cm,
∴DC=DE+EC=8cm,
故选:C.
10.如图,在△ABC中,AD⊥BC于点D,BD=DC,若BC=6,AD=7,则图中阴影部分图形的面积为 10.5 .
解:∵AD⊥BC,BC=6,AD=7,
∴△ABC的面积=×6×7=21,
∵AD⊥BC,BD=DC
∴AD是BC的垂直平分线,即AD是△ABC的对称轴,
∴阴影部分图形的面积=×S△ABC=10.5,
故答案为:10.5.
11.如图,在△ABC中,∠C=90°,∠B=22.5°,DE垂直平分AB交BC于点E,EC=2,则△ACE的面积为 2 .
解:∵DE垂直平分AB,
∴EA=EB,
∴∠EAB=∠B=22.5°,
∴∠AEC=∠EAB+∠B=45°,
∴AC=EC=2,
∴△ACE的面积=×AC×EC=×2×2=2,
故答案为:2.
12.如图,△ABC中,AB+AC=4,BC的垂直平分线l交AC于D,则△ABD的周长为 4 .
解:∵l是线段BC的垂直平分线,
∴DB=DC,
∴△ABD的周长=AB+AD+DB=AB+AD+DC=AB+AC=4,
故答案为:4.
13.如图,△ABC中,ED垂直平分AB,交AB于点D,交AC于点F,交BC的延长线于点E,若BF=6,CF=2,则AC的长为 8 .
解:∵ED垂直平分AB,BF=6,
∴AF=BF=6,
∵CF=2,
∴AC=AF+CF=6+2=8,
故答案为:8.
14.如图,在△ABC中,AC的垂直平分线分别交BC、AC于点D、G,AB的垂直平分线分别交BC、AB于点E、F,连接AD、AE,若C△ADE=13,DE=2,则BC= 9 .
解:∵DG是AC的垂直平分线,
∴DA=DC,
同理可得:EA=EB,
∵△ADE的周长为13,
∴AD+AE+DE=13,
∴DC+EB+DE=13,
∴DE+EC+EB+DE=13,
∵DE=2,
∴EC+EB=9,即BC=9,
故答案为:9.
15.如图,在△ABC中,∠BAC=120°,分别作AC,AB两边的垂直平分线PM、PN,垂足分别是点M、N,以下说法:①∠P=60°;②∠EAF=∠B+∠C;③PE=PF;④点P到点B和点C的距离相等.其中正确的是 ①②④ (填序号).
解:∵PM垂直平分AC,PN垂直平分AB,
∴∠PMA=∠PNA=90°,
∵∠P+∠PMA+∠PNA+∠BAC=360°,
∴∠P=360°﹣90°﹣90°﹣120°=60°,故①说法正确;
∵∠BAC=120°,
∴∠B+∠C=180°﹣120°=60°,
∵PM垂直平分AC,PN垂直平分AB,
∴EC=EA,FB=FA,
∴∠EAC=∠C,∠FAB=∠B,
∴∠EAC+∠FAB=60°,
∴∠EAF=∠BAC﹣∠EAC﹣∠FAB=∠BAC﹣(∠B+∠C)=120°﹣60°=60°,
∴∠EAF=∠B+∠C,故②说法正确;
∵△ABC不一定是等腰三角形,
∴PE与PF的大小无法确定,③说法错误;
连接PC、PA、PB,
∵PM垂直平分AC,PN垂直平分AB,
∴PC=PA,PB=PA,
∴PB=PC,即点P到点B和点C的距离相等,④说法正确,
故答案为:①②④.
16.如图,A、B表示两个仓库,要在A、B一侧的河岸边建造一个码头,使它到两个仓库的距离相等,码头应建造在什么位置?
解:连接AB,码头应建在线段AB的垂直平分线与靠近A、B一侧的河岸的交汇点处.
如图:点P就是码头应建的位置.
17.如图,在△ABC中,DE是AC的垂直平分线.
(1)若AC=6,△ABD的周长是13,则△ABC的周长是 19 ;
(2)若△ABC中,∠B=62°,∠C=36°,求∠BAD的度数.
解:(1)∵DE是AC的垂直平分线,
∴DA=DC,
∵△ABD的周长是13,
∴AB+AD+BD=AB+DC+BD=AB+BC=13,
∴△ABC的周长=AB+BC+AC=13+6=19,
故答案为:19;
(2)在△ABC中,∠B=62°,∠C=36°,
则∠BAC=180°﹣∠B﹣∠C=82°,
∵DA=DC,
∴∠DAC=∠C=36°,
∴∠BAD=∠BAC﹣∠DAC=82°﹣36°=46°.
18.如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接OB,OC.若△ADE的周长为12cm,△OBC的周长为32cm.
(1)求线段BC的长;
(2)连接OA,求线段OA的长;
(3)若∠BAC=n°(n>90),直接写出∠DAE的度数 (2n﹣180) °.
解:(1)∵l1是AB边的垂直平分线,
∴DA=DB,
∵l2是AC边的垂直平分线,
∴EA=EC,
BC=BD+DE+EC=DA+DE+EA=12cm;
(2)∵l1是AB边的垂直平分线,
∴OA=OB,
∵l2是AC边的垂直平分线,
∴OA=OC,
∵OB+OC+BC=32cm,
∴OA=OB=OC=10cm;
(3)∵∠BAC=n°,
∴∠ABC+∠ACB=(180﹣n)°,
∵DA=DB,EA=EC,
∴∠BAD=∠ABC,∠EAC=∠ACB,
∴∠DAE=∠BAC﹣∠BAD﹣∠EAC=n°﹣(180°﹣n°)=2n°﹣180°.
故答案为:(2n﹣180).
19.已知:△ABC是三边都不相等的三角形,点O和点P是这个三角形内部两点.
(1)如图①,如果点P是这个三角形三个内角平分线的交点,那么∠BPC和∠BAC有怎样的数量关系?请说明理由;
(2)如图②,如果点O是这个三角形三边垂直平分线的交点,那么∠BOC和∠BAC有怎样的数量关系?请说明理由;
(3)如图③,如果点P(三角形三个内角平分线的交点),点O(三角形三边垂直平分线的交点)同时在不等边△ABC的内部,那么∠BPC和∠BOC有怎样的数量关系?请直接回答.
解:(1)∠BPC=90°+∠BAC
∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC=∠ABC,∠PCB=∠ACB,
∴∠BPC=180°﹣(∠PBC+∠PCB)
=180°﹣(∠ABC+∠ACB)
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠BAC)
=90°+∠BAC;
(2)∠BOC=2∠BAC
如图,连接AO.
∵点O是这个三角形三边垂直平分线的交点,
∴OA=OB=OC,
∴∠OAB=∠OBA,∠OAC=∠OCA,∠OBC=∠OCB,
∴∠AOB=180°﹣2∠OAB,∠AOC=180°﹣2∠OAC,
∴∠BOC=360°﹣(∠AOB+∠AOC)
=360°﹣(180°﹣2∠OAB+180°﹣2∠OAC),
=2∠OAB+2∠OAC
=2∠BAC;
(3)4∠BPC﹣∠BOC=360°,
∵点P为三角形三个内角平分线的交点,
∴∠BPC=90°+∠BAC
由∠BAC=2∠BPC﹣180°
点O为三角形三边垂直平分线的交点
∠BOC=2∠BAC,
∴∠BOC=2(2∠BPC﹣180°)=4∠BPC﹣360°,
即4∠BPC﹣∠BOC=360°.
20.如图,四边形ABCD中,∠A=∠B=90°,AB=25cm,DA=15cm,CB=10cm.动点
E从A点出发,以2cm/s的速度向B点移动,设移动的时间为x秒.
(1)当x为何值时,点E在线段CD的垂直平分线上?
(2)在(1)的条件下,判断DE与CE的位置关系,并说明理由.
解:(1)设AE=acm,则BE=(25﹣a)cm,
∵点E在线段CD的垂直平分线上,
∴DE=CE,
由勾股定理得:AD2+AE2=DE2,BC2+BE2=CE2,
∴AD2+AE2=BC2+BE2,
即152+a2=102+(25﹣a)2,
解得:a=10,
即AE=10(cm),
∴x==5,
即当x=5时,点E在线段CD的垂直平分线上;
(2)DE与CE的位置关系是DE⊥CE,
理由是:∵△ADE≌△BEC,
∴∠ADE=∠CEB,
∵∠A=90°,
∴∠ADE+∠AED=90°,
∴∠AED+∠CEB=90°,
∴∠DEC=180°﹣(∠AED+∠CEB)=90°,
∴DE⊥CE.
21.如图,在Rt△ABC中,∠ACB=45°,∠BAC=90°,AB=AC,点D是AB的中点,AF⊥CD于H交BC于F,BE∥AC交AF的延长线于E.求证:BC垂直且平分DE.
证明:在△ADC中,∠DAH+∠ADH=90°,∠ACH+∠ADH=90°,
∴∠DAH=∠DCA,
∵∠BAC=90°,BE∥AC,
∴∠CAD=∠ABE=90°.
又∵AB=CA,
∴在△ABE与△CAD中,
∴△ABE≌△CAD(ASA),
∴AD=BE,
又∵AD=BD,
∴BD=BE,
在Rt△ABC中,∠ACB=45°,∠BAC=90°,AB=AC,
故∠ABC=45°.
∵BE∥AC,
∴∠EBD=90°,∠EBF=90°﹣45°=45°,
∴△DBP≌△EBP(SAS),
∴DP=EP,
即可得出BC垂直且平分DE.
1.到三角形三个顶点距离都相等的点是( )
A.三角形的三条角平分线的交点 B.三角形的三边垂直平分线的交点
C.三角形的三条高线的交点 D.三角形的三条中线的交点
2.如图,△ABC中,DE是AC的垂直平分线,△ABC的周长为21cm,△ABD的周长为13cm,则AE长为( )
A.8cm B.6cm C.4cm D.10cm
3.如图,在△ABC中,BC边的中垂线DE,分别与AB、BC边交于点D、E两点,连接CD,边AC的中垂线FG分别与CD、AC边交于点F、G两点,连接AF.若△ADF的周长为13,AD=4,则BD的长为( )
A.4 B.9 C.13 D.17
4.如图,在△ABC中,直线l为边BC的垂直平分线,l交AC于点Q,∠ABC的角平分线与l相交于点P.若∠BAC=60°,∠ACP=24°,则∠PQC是( )
A.34° B.36° C.44° D.46°
5.如图,直线l,m相交于点O.P为这两直线外一点,且OP=2.8.若点P关于直线l,m的对称点分别是点P1,P2,则P1,P2之间的距离可能是( )
A.0 B.5 C.6 D.7
6.如图,电信部门要在公路l旁修建一座移动信号发射塔.按照设计要求,发射塔到两个城镇M,N的距离必须相等,则发射塔应该建在( )
A.A处 B.B处 C.C处 D.D处
7.如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )
A.1对 B.2对 C.3对 D.4对
8.已知:如图,∠AOB内一点P,P1,P2分别P是关于OA、OB的对称点,P1P2交OA于M,交OB于N,若P1P2=5cm,则△PMN的周长是( )
A.3cm B.4cm C.5cm D.6cm
9.如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.若△ABC的周长为26cm,AC=10cm,则DC的长为( )
A.10cm B.9cm C.8cm D.7cm
10.如图,在△ABC中,AD⊥BC于点D,BD=DC,若BC=6,AD=7,则图中阴影部分图形的面积为 .
11.如图,在△ABC中,∠C=90°,∠B=22.5°,DE垂直平分AB交BC于点E,EC=2,则△ACE的面积为 .
12.如图,△ABC中,AB+AC=4,BC的垂直平分线l交AC于D,则△ABD的周长为 .
13.如图,△ABC中,ED垂直平分AB,交AB于点D,交AC于点F,交BC的延长线于点E,若BF=6,CF=2,则AC的长为 .
14.如图,在△ABC中,AC的垂直平分线分别交BC、AC于点D、G,AB的垂直平分线分别交BC、AB于点E、F,连接AD、AE,若C△ADE=13,DE=2,则BC= .
15.如图,在△ABC中,∠BAC=120°,分别作AC,AB两边的垂直平分线PM、PN,垂足分别是点M、N,以下说法:①∠P=60°;②∠EAF=∠B+∠C;③PE=PF;④点P到点B和点C的距离相等.其中正确的是 (填序号).
16.如图,A、B表示两个仓库,要在A、B一侧的河岸边建造一个码头,使它到两个仓库的距离相等,码头应建造在什么位置?
17.如图,在△ABC中,DE是AC的垂直平分线.
(1)若AC=6,△ABD的周长是13,则△ABC的周长是 ;
(2)若△ABC中,∠B=62°,∠C=36°,求∠BAD的度数.
18.如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接OB,OC.若△ADE的周长为12cm,△OBC的周长为32cm.
(1)求线段BC的长;
(2)连接OA,求线段OA的长;
(3)若∠BAC=n°(n>90),直接写出∠DAE的度数 °.
19.已知:△ABC是三边都不相等的三角形,点O和点P是这个三角形内部两点.
(1)如图①,如果点P是这个三角形三个内角平分线的交点,那么∠BPC和∠BAC有怎样的数量关系?请说明理由;
(2)如图②,如果点O是这个三角形三边垂直平分线的交点,那么∠BOC和∠BAC有怎样的数量关系?请说明理由;
(3)如图③,如果点P(三角形三个内角平分线的交点),点O(三角形三边垂直平分线的交点)同时在不等边△ABC的内部,那么∠BPC和∠BOC有怎样的数量关系?请直接回答.
20.如图,四边形ABCD中,∠A=∠B=90°,AB=25cm,DA=15cm,CB=10cm.动点
E从A点出发,以2cm/s的速度向B点移动,设移动的时间为x秒.
(1)当x为何值时,点E在线段CD的垂直平分线上?
(2)在(1)的条件下,判断DE与CE的位置关系,并说明理由.
21.如图,在Rt△ABC中,∠ACB=45°,∠BAC=90°,AB=AC,点D是AB的中点,AF⊥CD于H交BC于F,BE∥AC交AF的延长线于E.求证:BC垂直且平分DE.
参考答案
1.到三角形三个顶点距离都相等的点是( )
A.三角形的三条角平分线的交点
B.三角形的三边垂直平分线的交点
C.三角形的三条高线的交点
D.三角形的三条中线的交点
解:∵到三角形的一边的两端点距离相等的点在这边的垂直平分线上,
∴到三角形三个顶点的距离都相等的点是这个三角形的三条边的垂直平分线的交点,
故选:B.
2.如图,△ABC中,DE是AC的垂直平分线,△ABC的周长为21cm,△ABD的周长为13cm,则AE长为( )
A.8cm B.6cm C.4cm D.10cm
解:∵DE是AC的垂直平分线,
∴DA=DC,AE=EC,
∵△ABC的周长为21cm,
∴AB+BC+AC=21cm,
∵△ABD的周长为13cm,
∴AB+BD+AD=AB+BD+DC=AB+BC=13cm,
∴AC=8cm,
∴AE=4cm,
故选:C.
3.如图,在△ABC中,BC边的中垂线DE,分别与AB、BC边交于点D、E两点,连接CD,边AC的中垂线FG分别与CD、AC边交于点F、G两点,连接AF.若△ADF的周长为13,AD=4,则BD的长为( )
A.4 B.9 C.13 D.17
解:∵边AC的中垂线FG分别与CD、AC边交于点F、G两点,连接AF.
∴CF=AF,
∴△ADF的周长=AF+DF+AD=CF+DF+AD=CD+AD=13,
∵AD=4,
∴CD=9,
∵DE是BC边的中垂线,
∴BD=CD=9,
故选:B.
4.如图,在△ABC中,直线l为边BC的垂直平分线,l交AC于点Q,∠ABC的角平分线与l相交于点P.若∠BAC=60°,∠ACP=24°,则∠PQC是( )
A.34° B.36° C.44° D.46°
解:∵BP平分∠ABC,
∴∠ABP=∠CBP,
∵直线l是线段BC的垂直平分线,
∴BP=CP,
∴∠CBP=∠BCP,
∴∠ABP=∠BCP,
∵∠A+∠ACB+∠ABC=180°,∠A=60°,∠ACP=24°,
∴3∠ABP+24°+60°=180°,
∴∠ABP=32°,
∴∠PBC=∠PCB=32°,
∴∠PQC=×(180°﹣32°﹣32°)﹣24°=58°﹣24°=34°,
故选:A.
5.如图,直线l,m相交于点O.P为这两直线外一点,且OP=2.8.若点P关于直线l,m的对称点分别是点P1,P2,则P1,P2之间的距离可能是( )
A.0 B.5 C.6 D.7
解:连接OP1,OP2,P1P2,
∵点P关于直线l,m的对称点分别是点P1,P2,
∴OP1=OP=2.8,OP=OP2=2.8,
OP1+OP2>P1P2,
0<P1P2<5.6,
故选:B.
6.如图,电信部门要在公路l旁修建一座移动信号发射塔.按照设计要求,发射塔到两个城镇M,N的距离必须相等,则发射塔应该建在( )
A.A处 B.B处 C.C处 D.D处
解:
根据作图可知:EF是线段MN的垂直平分线,
所以EF上的点到M、N的距离相等,
即发射塔应该建在C处,
故选:C.
7.如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )
A.1对 B.2对 C.3对 D.4对
解:∵EF是AC的垂直平分线,
∴OA=OC,
又∵OE=OE,
∴Rt△AOE≌Rt△COE,
∵AB=AC,D是BC的中点,
∴AD⊥BC,
∴△ABC关于直线AD轴对称,
∴△AOC≌△AOB,△BOD≌△COD,△ABD≌△ACD,
综上所述,全等三角形共有4对.
故选:D.
8.已知:如图,∠AOB内一点P,P1,P2分别P是关于OA、OB的对称点,P1P2交OA于M,交OB于N,若P1P2=5cm,则△PMN的周长是( )
A.3cm B.4cm C.5cm D.6cm
解:∵P与P1关于OA对称,
∴OA为线段PP1的垂直平分线,
∴MP=MP1,
同理,P与P2关于OB对称,
∴OB为线段PP2的垂直平分线,
∴NP=NP2,
∴P1P2=P1M+MN+NP2=MP+MN+NP=5cm,
则△PMN的周长为5cm.
故选:C.
9.如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.若△ABC的周长为26cm,AC=10cm,则DC的长为( )
A.10cm B.9cm C.8cm D.7cm
解:∵△ABC的周长为26cm,AC=10cm,
∴AB+BC=16cm,
∴AB+BE+EC=16cm,
即2DE+2EC=16cm,
∴DE+EC=8cm,
∴DC=DE+EC=8cm,
故选:C.
10.如图,在△ABC中,AD⊥BC于点D,BD=DC,若BC=6,AD=7,则图中阴影部分图形的面积为 10.5 .
解:∵AD⊥BC,BC=6,AD=7,
∴△ABC的面积=×6×7=21,
∵AD⊥BC,BD=DC
∴AD是BC的垂直平分线,即AD是△ABC的对称轴,
∴阴影部分图形的面积=×S△ABC=10.5,
故答案为:10.5.
11.如图,在△ABC中,∠C=90°,∠B=22.5°,DE垂直平分AB交BC于点E,EC=2,则△ACE的面积为 2 .
解:∵DE垂直平分AB,
∴EA=EB,
∴∠EAB=∠B=22.5°,
∴∠AEC=∠EAB+∠B=45°,
∴AC=EC=2,
∴△ACE的面积=×AC×EC=×2×2=2,
故答案为:2.
12.如图,△ABC中,AB+AC=4,BC的垂直平分线l交AC于D,则△ABD的周长为 4 .
解:∵l是线段BC的垂直平分线,
∴DB=DC,
∴△ABD的周长=AB+AD+DB=AB+AD+DC=AB+AC=4,
故答案为:4.
13.如图,△ABC中,ED垂直平分AB,交AB于点D,交AC于点F,交BC的延长线于点E,若BF=6,CF=2,则AC的长为 8 .
解:∵ED垂直平分AB,BF=6,
∴AF=BF=6,
∵CF=2,
∴AC=AF+CF=6+2=8,
故答案为:8.
14.如图,在△ABC中,AC的垂直平分线分别交BC、AC于点D、G,AB的垂直平分线分别交BC、AB于点E、F,连接AD、AE,若C△ADE=13,DE=2,则BC= 9 .
解:∵DG是AC的垂直平分线,
∴DA=DC,
同理可得:EA=EB,
∵△ADE的周长为13,
∴AD+AE+DE=13,
∴DC+EB+DE=13,
∴DE+EC+EB+DE=13,
∵DE=2,
∴EC+EB=9,即BC=9,
故答案为:9.
15.如图,在△ABC中,∠BAC=120°,分别作AC,AB两边的垂直平分线PM、PN,垂足分别是点M、N,以下说法:①∠P=60°;②∠EAF=∠B+∠C;③PE=PF;④点P到点B和点C的距离相等.其中正确的是 ①②④ (填序号).
解:∵PM垂直平分AC,PN垂直平分AB,
∴∠PMA=∠PNA=90°,
∵∠P+∠PMA+∠PNA+∠BAC=360°,
∴∠P=360°﹣90°﹣90°﹣120°=60°,故①说法正确;
∵∠BAC=120°,
∴∠B+∠C=180°﹣120°=60°,
∵PM垂直平分AC,PN垂直平分AB,
∴EC=EA,FB=FA,
∴∠EAC=∠C,∠FAB=∠B,
∴∠EAC+∠FAB=60°,
∴∠EAF=∠BAC﹣∠EAC﹣∠FAB=∠BAC﹣(∠B+∠C)=120°﹣60°=60°,
∴∠EAF=∠B+∠C,故②说法正确;
∵△ABC不一定是等腰三角形,
∴PE与PF的大小无法确定,③说法错误;
连接PC、PA、PB,
∵PM垂直平分AC,PN垂直平分AB,
∴PC=PA,PB=PA,
∴PB=PC,即点P到点B和点C的距离相等,④说法正确,
故答案为:①②④.
16.如图,A、B表示两个仓库,要在A、B一侧的河岸边建造一个码头,使它到两个仓库的距离相等,码头应建造在什么位置?
解:连接AB,码头应建在线段AB的垂直平分线与靠近A、B一侧的河岸的交汇点处.
如图:点P就是码头应建的位置.
17.如图,在△ABC中,DE是AC的垂直平分线.
(1)若AC=6,△ABD的周长是13,则△ABC的周长是 19 ;
(2)若△ABC中,∠B=62°,∠C=36°,求∠BAD的度数.
解:(1)∵DE是AC的垂直平分线,
∴DA=DC,
∵△ABD的周长是13,
∴AB+AD+BD=AB+DC+BD=AB+BC=13,
∴△ABC的周长=AB+BC+AC=13+6=19,
故答案为:19;
(2)在△ABC中,∠B=62°,∠C=36°,
则∠BAC=180°﹣∠B﹣∠C=82°,
∵DA=DC,
∴∠DAC=∠C=36°,
∴∠BAD=∠BAC﹣∠DAC=82°﹣36°=46°.
18.如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接OB,OC.若△ADE的周长为12cm,△OBC的周长为32cm.
(1)求线段BC的长;
(2)连接OA,求线段OA的长;
(3)若∠BAC=n°(n>90),直接写出∠DAE的度数 (2n﹣180) °.
解:(1)∵l1是AB边的垂直平分线,
∴DA=DB,
∵l2是AC边的垂直平分线,
∴EA=EC,
BC=BD+DE+EC=DA+DE+EA=12cm;
(2)∵l1是AB边的垂直平分线,
∴OA=OB,
∵l2是AC边的垂直平分线,
∴OA=OC,
∵OB+OC+BC=32cm,
∴OA=OB=OC=10cm;
(3)∵∠BAC=n°,
∴∠ABC+∠ACB=(180﹣n)°,
∵DA=DB,EA=EC,
∴∠BAD=∠ABC,∠EAC=∠ACB,
∴∠DAE=∠BAC﹣∠BAD﹣∠EAC=n°﹣(180°﹣n°)=2n°﹣180°.
故答案为:(2n﹣180).
19.已知:△ABC是三边都不相等的三角形,点O和点P是这个三角形内部两点.
(1)如图①,如果点P是这个三角形三个内角平分线的交点,那么∠BPC和∠BAC有怎样的数量关系?请说明理由;
(2)如图②,如果点O是这个三角形三边垂直平分线的交点,那么∠BOC和∠BAC有怎样的数量关系?请说明理由;
(3)如图③,如果点P(三角形三个内角平分线的交点),点O(三角形三边垂直平分线的交点)同时在不等边△ABC的内部,那么∠BPC和∠BOC有怎样的数量关系?请直接回答.
解:(1)∠BPC=90°+∠BAC
∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC=∠ABC,∠PCB=∠ACB,
∴∠BPC=180°﹣(∠PBC+∠PCB)
=180°﹣(∠ABC+∠ACB)
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠BAC)
=90°+∠BAC;
(2)∠BOC=2∠BAC
如图,连接AO.
∵点O是这个三角形三边垂直平分线的交点,
∴OA=OB=OC,
∴∠OAB=∠OBA,∠OAC=∠OCA,∠OBC=∠OCB,
∴∠AOB=180°﹣2∠OAB,∠AOC=180°﹣2∠OAC,
∴∠BOC=360°﹣(∠AOB+∠AOC)
=360°﹣(180°﹣2∠OAB+180°﹣2∠OAC),
=2∠OAB+2∠OAC
=2∠BAC;
(3)4∠BPC﹣∠BOC=360°,
∵点P为三角形三个内角平分线的交点,
∴∠BPC=90°+∠BAC
由∠BAC=2∠BPC﹣180°
点O为三角形三边垂直平分线的交点
∠BOC=2∠BAC,
∴∠BOC=2(2∠BPC﹣180°)=4∠BPC﹣360°,
即4∠BPC﹣∠BOC=360°.
20.如图,四边形ABCD中,∠A=∠B=90°,AB=25cm,DA=15cm,CB=10cm.动点
E从A点出发,以2cm/s的速度向B点移动,设移动的时间为x秒.
(1)当x为何值时,点E在线段CD的垂直平分线上?
(2)在(1)的条件下,判断DE与CE的位置关系,并说明理由.
解:(1)设AE=acm,则BE=(25﹣a)cm,
∵点E在线段CD的垂直平分线上,
∴DE=CE,
由勾股定理得:AD2+AE2=DE2,BC2+BE2=CE2,
∴AD2+AE2=BC2+BE2,
即152+a2=102+(25﹣a)2,
解得:a=10,
即AE=10(cm),
∴x==5,
即当x=5时,点E在线段CD的垂直平分线上;
(2)DE与CE的位置关系是DE⊥CE,
理由是:∵△ADE≌△BEC,
∴∠ADE=∠CEB,
∵∠A=90°,
∴∠ADE+∠AED=90°,
∴∠AED+∠CEB=90°,
∴∠DEC=180°﹣(∠AED+∠CEB)=90°,
∴DE⊥CE.
21.如图,在Rt△ABC中,∠ACB=45°,∠BAC=90°,AB=AC,点D是AB的中点,AF⊥CD于H交BC于F,BE∥AC交AF的延长线于E.求证:BC垂直且平分DE.
证明:在△ADC中,∠DAH+∠ADH=90°,∠ACH+∠ADH=90°,
∴∠DAH=∠DCA,
∵∠BAC=90°,BE∥AC,
∴∠CAD=∠ABE=90°.
又∵AB=CA,
∴在△ABE与△CAD中,
∴△ABE≌△CAD(ASA),
∴AD=BE,
又∵AD=BD,
∴BD=BE,
在Rt△ABC中,∠ACB=45°,∠BAC=90°,AB=AC,
故∠ABC=45°.
∵BE∥AC,
∴∠EBD=90°,∠EBF=90°﹣45°=45°,
∴△DBP≌△EBP(SAS),
∴DP=EP,
即可得出BC垂直且平分DE.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
