2021-2022学年华东师大版七年级数学上册第三章 整式的加减 单元测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版七年级数学上册第三章 整式的加减 单元测试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 132.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 10:10:46 | ||
图片预览




文档简介
第三章整式的加减单元测试卷 2021-2022学年华东师大版七年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
下列各式:-2;-;m+n;-b;-中,单项式的个数有( )
A. 个 B. 个 C. 个 D. 个
甲数的比乙数小1,设甲数为x,则乙数为( )
A. B. C. D.
代数式---1按x的升幂排列,正确的是( )
A. B.
C. D.
下列去括号运算中,错误的是( )
A.
B.
C.
D.
若-与是同类项,则a+b的值为( )
A. B. C. D.
若A和B都是4次多项式,则A+B一定是( )
A. 次多项式 B. 次多项式
C. 次数不高于次的整式 D. 次数不低于次的整式
如图,阴影部分的面积是( )
A. B.
C. D.
如图,为做一个试管架,在a cm长的木条上钻了4个圆孔,每个孔直径为2 cm,则x等于( )
A. B. C. D.
某同学计算一个多项式加上xy-3yz-2xz时,误认为减去此式,计算出的错误结果为xy-2yz+3xz,则正确的结果是( )
A. B. C. D.
把灰色三角形按如图所示的规律拼图案,其中第个图案中有1个灰色三角形,第个图案中有3个灰色三角形,第个图案中有6个灰色三角形,,按此规律排列下去,则第个图案中灰色三角形的个数为( )
A. B. C. D.
二、填空题(本大题共5小题,共15分)
单项式-的系数是 ,次数是 .
老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:+(-+5x-7)=-+3x-6,则所捂的多项式是 .
随着通讯市场的竞争日益激烈,为了占领市场,甲公司推出的优惠措施是每分钟降低a元后,再下调25%;乙公司推出的优惠措施是每分钟下调25%,再降低a元.若甲、乙两公司原来每分钟的收费相同,则推出优惠措施后收费较便宜的是 公司.
已知代数式-5x+6的值为8,则-x+6的值为 .
如图,将若干个三角形、正方形和圆按一定规律从左向右排列,那么第2020个图形是 .
三、解答题(本大题共9小题,共75分)
先化简,再求值:
(1)3m+4n-[2m+(5m-2n)-3n],其中m==2;
(2)-,其中|x-1|+=0.
已知与|b+1|互为相反数,求-[-(2ab-)-]-ab的值.
小明对代数式+ax-y+6-+3x-5y-1进行化简后,发现化简的结果中没有含x的项,请求出代数式的值.
已知:A=-3ab-5a-1,B=-+ab-1.
(1)求3A+6B;
(2)当a=-1,b=2时,求(1)中式子的值.
【阅读理解】小海喜欢研究数学问题,在计算整式加减(--7+5x)+(2x+)的时候,想到了小学的列竖式加减法,令A=--7+5x,B=2x+,然后将两个整式关于x进行降幂排列,A=-+5x-7,B=+2x,最后只要写出其各项系数,对齐同类项进行竖式计算如下:
所以(--7+5x)+(2x+)=-+7x-7.
【模仿解题】若A=-+-+,B=+--,请你按照小海的方法,先对整式A,B关于某个字母进行降幂排列,再写出其各项系数,进行竖式计算A-B,并写出A-B的值.
为节约用水,某市规定三口之家每月标准用水量为15立方米,超过部分加价收费,假设不超过部分水费为1.5元/立方米,超过部分水费为3元/立方米.
(1)如果这家某月用水a立方米,请用代数式分别表示这家按标准用水和超出标准用水时各应缴纳的水费;
(2)如果这家某月用水20立方米,那么该月应交多少水费
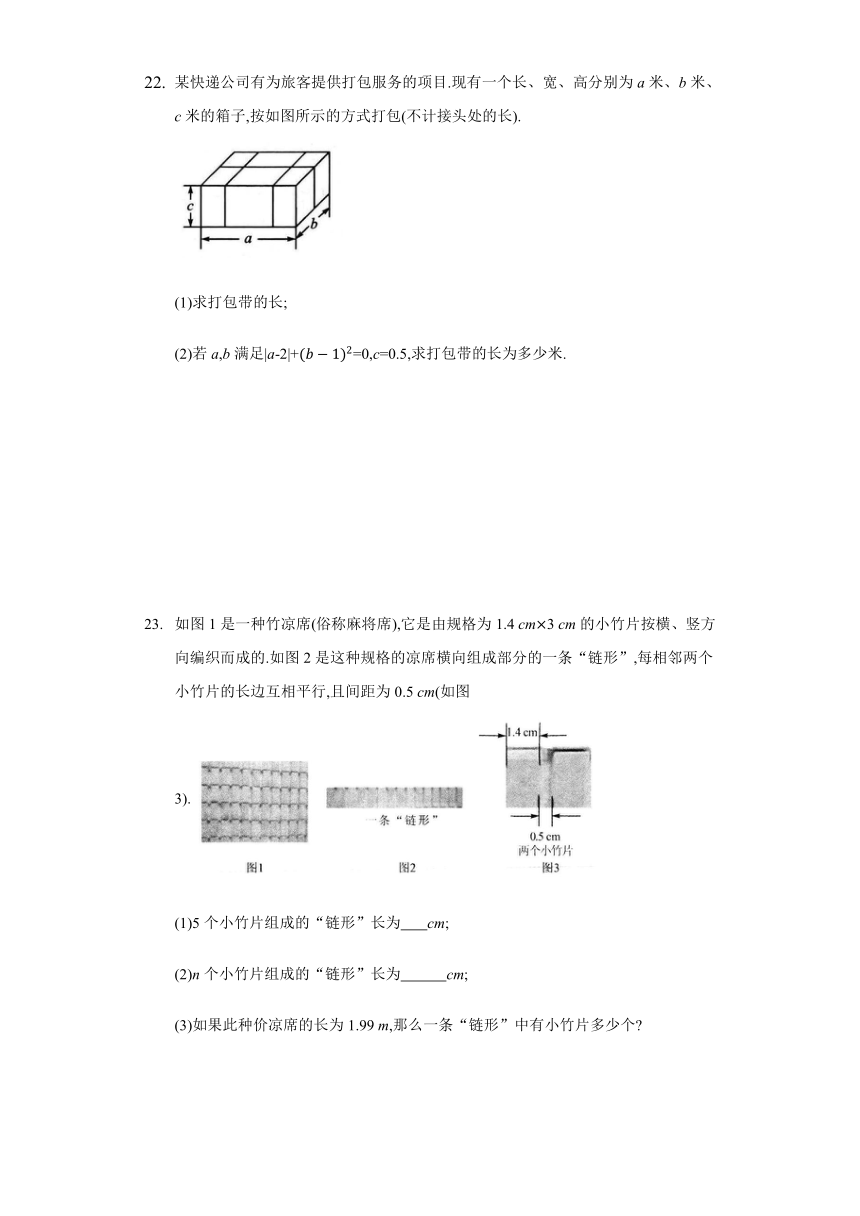
某快递公司有为旅客提供打包服务的项目.现有一个长、宽、高分别为a米、b米、c米的箱子,按如图所示的方式打包(不计接头处的长).
(1)求打包带的长;
(2)若a,b满足|a-2|+=0,c=0.5,求打包带的长为多少米.
如图1是一种竹凉席(俗称麻将席),它是由规格为1.4 cm3 cm的小竹片按横、竖方向编织而成的.如图2是这种规格的凉席横向组成部分的一条“链形”,每相邻两个小竹片的长边互相平行,且间距为0.5 cm(如图3).
(1)5个小竹片组成的“链形”长为 cm;
(2)n个小竹片组成的“链形”长为 cm;
(3)如果此种价凉席的长为1.99 m,那么一条“链形”中有小竹片多少个
某家具厂生产一种课桌和椅子,课桌每张定价200元,椅子每把定价80元,厂方在开展促销活动期间,向客户提供两种优惠方案:
方案一:每买一张课桌就赠送一把椅子;
方案二:课桌和椅子都按定价的80%付款.某校计划添置100张课桌和x把椅子.
(1)若x=100,请计算哪种方案划算;
(2)若x>100,请用含x的式子分别把两种方案的费用表示出来;
(3)若x=300,如果两种方案可以同时使用,请帮助学校设计一种最省钱的方案.
参考答案
1.【答案】C
2.【答案】B
3.【答案】D
4.【答案】B
5.【答案】C
6.【答案】C
7.【答案】A
8.【答案】D
9.【答案】B
10.【答案】B
11.【答案】- 4
12.【答案】-2x+1
13.【答案】乙
14.【答案】7
15.【答案】□
16.【答案】解:(1)原式=3m+4n-2m-5m+2n+3n
=-4m+9n.
当m==2,即m=2,n=时,原式=-4m+9n=-42+9=-.
(2)-
=-5xy++3xy-+2xy-
=+.
因为|x-1|+=0,
所以x-1=0且y+2=0,
所以x=1,y=-2.
所以原式=+=+=.
17.【答案】解:由题意,得+|b+1|=0,
因为0,|b+1|0,所以=0,|b+1|=0.
所以a=2,b=-1.
原式=-(-2ab+-)-ab
=-+2ab-+-ab
=ab+.
当a=2,b=-1时,原式=2(-1)+4=-2+44=14.
18.【答案】解:原式=(2-2b)+(a+3)x-6y+5.
因为化简的结果中没有含x的项,
所以2-2b=0,a+3=0.解得a=-3,b=1.
则=16.
19.【答案】解:(1)因为A=-3ab-5a-1,B=-+ab-1,
所以3A+6B=3(-3ab-5a-1)+6(-+ab-1)
=-9ab-15a-3-+6ab-6
=-3ab-15a-9.
(2)当a=-1,b=2时,原式=-3(-1)2-15(-1)-9=12.
20.【答案】解:将两个整式关于x进行降幂排列,
A=+--,B=+--,
各项系数进行竖式计算:
所以A-B=---+.
21.【答案】解:(1)标准用水水费为:1.5a元(0< a 15);
超出标准用水水费为:(a-15)3+151.5=(3a-22.5)元(a>15).
(2)如果这家某月用水20立方米,那么该月应交37.5元水费.
22.【答案】解:(1)打包带的长(不计接头处的长)为(2a+4b+6c)米.
(2)因为|a-2|+=0,所以a-2=0,b-1=0.
因为a=2,b=1.所以2a+4b+6c=22+41+60.5=11.
答:打包带的长为11米.
23.【答案】解:(1)9;
(2)(1.9n-0.5);
(3)设有小竹片n个,依题意,得1.9n-0.5=199,解得n=105.
答:如果此种竹凉席的长为1.99 m,那么一条“链形”中有小竹片105个.
24.【答案】解:(1)当x=100时,
方案一:100200=20000(元),
方案二:100(200+80)80%=22400(元),
因为20000<22400,所以方案一划算.
(2)当x>100时,
方案一:100200+80(x-100)=80x+12000,
方案二:(100200+80x)80%=64x+16000.
(3)当x=300时,
按方案一购买:80300+12000=36000(元);
按方案二购买:64300+16000=35200(元);
先按方案一购买100张课桌,同时送100把椅子;
再按方案二购买200把椅子,100200+8020080%=32800(元),
36000>35200>32800,
即先按方案一购买100张课桌,同时送100把椅子;
再按方案二购买200把椅子最省钱.
第2页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
下列各式:-2;-;m+n;-b;-中,单项式的个数有( )
A. 个 B. 个 C. 个 D. 个
甲数的比乙数小1,设甲数为x,则乙数为( )
A. B. C. D.
代数式---1按x的升幂排列,正确的是( )
A. B.
C. D.
下列去括号运算中,错误的是( )
A.
B.
C.
D.
若-与是同类项,则a+b的值为( )
A. B. C. D.
若A和B都是4次多项式,则A+B一定是( )
A. 次多项式 B. 次多项式
C. 次数不高于次的整式 D. 次数不低于次的整式
如图,阴影部分的面积是( )
A. B.
C. D.
如图,为做一个试管架,在a cm长的木条上钻了4个圆孔,每个孔直径为2 cm,则x等于( )
A. B. C. D.
某同学计算一个多项式加上xy-3yz-2xz时,误认为减去此式,计算出的错误结果为xy-2yz+3xz,则正确的结果是( )
A. B. C. D.
把灰色三角形按如图所示的规律拼图案,其中第个图案中有1个灰色三角形,第个图案中有3个灰色三角形,第个图案中有6个灰色三角形,,按此规律排列下去,则第个图案中灰色三角形的个数为( )
A. B. C. D.
二、填空题(本大题共5小题,共15分)
单项式-的系数是 ,次数是 .
老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:+(-+5x-7)=-+3x-6,则所捂的多项式是 .
随着通讯市场的竞争日益激烈,为了占领市场,甲公司推出的优惠措施是每分钟降低a元后,再下调25%;乙公司推出的优惠措施是每分钟下调25%,再降低a元.若甲、乙两公司原来每分钟的收费相同,则推出优惠措施后收费较便宜的是 公司.
已知代数式-5x+6的值为8,则-x+6的值为 .
如图,将若干个三角形、正方形和圆按一定规律从左向右排列,那么第2020个图形是 .
三、解答题(本大题共9小题,共75分)
先化简,再求值:
(1)3m+4n-[2m+(5m-2n)-3n],其中m==2;
(2)-,其中|x-1|+=0.
已知与|b+1|互为相反数,求-[-(2ab-)-]-ab的值.
小明对代数式+ax-y+6-+3x-5y-1进行化简后,发现化简的结果中没有含x的项,请求出代数式的值.
已知:A=-3ab-5a-1,B=-+ab-1.
(1)求3A+6B;
(2)当a=-1,b=2时,求(1)中式子的值.
【阅读理解】小海喜欢研究数学问题,在计算整式加减(--7+5x)+(2x+)的时候,想到了小学的列竖式加减法,令A=--7+5x,B=2x+,然后将两个整式关于x进行降幂排列,A=-+5x-7,B=+2x,最后只要写出其各项系数,对齐同类项进行竖式计算如下:
所以(--7+5x)+(2x+)=-+7x-7.
【模仿解题】若A=-+-+,B=+--,请你按照小海的方法,先对整式A,B关于某个字母进行降幂排列,再写出其各项系数,进行竖式计算A-B,并写出A-B的值.
为节约用水,某市规定三口之家每月标准用水量为15立方米,超过部分加价收费,假设不超过部分水费为1.5元/立方米,超过部分水费为3元/立方米.
(1)如果这家某月用水a立方米,请用代数式分别表示这家按标准用水和超出标准用水时各应缴纳的水费;
(2)如果这家某月用水20立方米,那么该月应交多少水费
某快递公司有为旅客提供打包服务的项目.现有一个长、宽、高分别为a米、b米、c米的箱子,按如图所示的方式打包(不计接头处的长).
(1)求打包带的长;
(2)若a,b满足|a-2|+=0,c=0.5,求打包带的长为多少米.
如图1是一种竹凉席(俗称麻将席),它是由规格为1.4 cm3 cm的小竹片按横、竖方向编织而成的.如图2是这种规格的凉席横向组成部分的一条“链形”,每相邻两个小竹片的长边互相平行,且间距为0.5 cm(如图3).
(1)5个小竹片组成的“链形”长为 cm;
(2)n个小竹片组成的“链形”长为 cm;
(3)如果此种价凉席的长为1.99 m,那么一条“链形”中有小竹片多少个
某家具厂生产一种课桌和椅子,课桌每张定价200元,椅子每把定价80元,厂方在开展促销活动期间,向客户提供两种优惠方案:
方案一:每买一张课桌就赠送一把椅子;
方案二:课桌和椅子都按定价的80%付款.某校计划添置100张课桌和x把椅子.
(1)若x=100,请计算哪种方案划算;
(2)若x>100,请用含x的式子分别把两种方案的费用表示出来;
(3)若x=300,如果两种方案可以同时使用,请帮助学校设计一种最省钱的方案.
参考答案
1.【答案】C
2.【答案】B
3.【答案】D
4.【答案】B
5.【答案】C
6.【答案】C
7.【答案】A
8.【答案】D
9.【答案】B
10.【答案】B
11.【答案】- 4
12.【答案】-2x+1
13.【答案】乙
14.【答案】7
15.【答案】□
16.【答案】解:(1)原式=3m+4n-2m-5m+2n+3n
=-4m+9n.
当m==2,即m=2,n=时,原式=-4m+9n=-42+9=-.
(2)-
=-5xy++3xy-+2xy-
=+.
因为|x-1|+=0,
所以x-1=0且y+2=0,
所以x=1,y=-2.
所以原式=+=+=.
17.【答案】解:由题意,得+|b+1|=0,
因为0,|b+1|0,所以=0,|b+1|=0.
所以a=2,b=-1.
原式=-(-2ab+-)-ab
=-+2ab-+-ab
=ab+.
当a=2,b=-1时,原式=2(-1)+4=-2+44=14.
18.【答案】解:原式=(2-2b)+(a+3)x-6y+5.
因为化简的结果中没有含x的项,
所以2-2b=0,a+3=0.解得a=-3,b=1.
则=16.
19.【答案】解:(1)因为A=-3ab-5a-1,B=-+ab-1,
所以3A+6B=3(-3ab-5a-1)+6(-+ab-1)
=-9ab-15a-3-+6ab-6
=-3ab-15a-9.
(2)当a=-1,b=2时,原式=-3(-1)2-15(-1)-9=12.
20.【答案】解:将两个整式关于x进行降幂排列,
A=+--,B=+--,
各项系数进行竖式计算:
所以A-B=---+.
21.【答案】解:(1)标准用水水费为:1.5a元(0< a 15);
超出标准用水水费为:(a-15)3+151.5=(3a-22.5)元(a>15).
(2)如果这家某月用水20立方米,那么该月应交37.5元水费.
22.【答案】解:(1)打包带的长(不计接头处的长)为(2a+4b+6c)米.
(2)因为|a-2|+=0,所以a-2=0,b-1=0.
因为a=2,b=1.所以2a+4b+6c=22+41+60.5=11.
答:打包带的长为11米.
23.【答案】解:(1)9;
(2)(1.9n-0.5);
(3)设有小竹片n个,依题意,得1.9n-0.5=199,解得n=105.
答:如果此种竹凉席的长为1.99 m,那么一条“链形”中有小竹片105个.
24.【答案】解:(1)当x=100时,
方案一:100200=20000(元),
方案二:100(200+80)80%=22400(元),
因为20000<22400,所以方案一划算.
(2)当x>100时,
方案一:100200+80(x-100)=80x+12000,
方案二:(100200+80x)80%=64x+16000.
(3)当x=300时,
按方案一购买:80300+12000=36000(元);
按方案二购买:64300+16000=35200(元);
先按方案一购买100张课桌,同时送100把椅子;
再按方案二购买200把椅子,100200+8020080%=32800(元),
36000>35200>32800,
即先按方案一购买100张课桌,同时送100把椅子;
再按方案二购买200把椅子最省钱.
第2页,共2页
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
